地震作用下连续刚构桥的受力分析

2017-07-05刘瑜上海城建市政工程集团有限公司上海200065

福建交通科技 2017年3期

刘瑜（上海城建市政工程（集团）有限公司，上海200065）

地震作用下连续刚构桥的受力分析

刘瑜
（上海城建市政工程（集团）有限公司，上海200065）

连续刚构桥是大桥、特大桥梁的常见桥型，随着新版《中国地震动参数区划图》的实施，对桥梁抗震提出了更高的要求。抗震设计贯穿桥梁设计全过程，准确进行地震模拟计算是抗震设计的保证。本文通过对某连续刚构桥梁施工过程的模拟以及成桥状态下桥梁结构地震响应的分析，研究地震作用对于连续刚构桥梁受力分析的影响。

连续刚构施工过程有限元分析地震响应

1 工程概况

连续刚构桥梁位于安徽省某省级公路上，桥梁全长280m，跨径布置为75+130+75m，属于大型桥梁（见图1）。桥梁分两幅，单幅桥面宽度12m，单向三车道，横断面为单箱单室混凝土箱梁。上部结构采用连续刚构体系，跨中截面梁高3.6m，中支墩截面梁高8.0m，梁底采用二次抛物线变化。下部结构主墩采用双肢薄壁墩，桥台采用桩柱式台，桩基础。施工采用挂篮分节段悬臂施工工法，分为0#~19#共计20个节段，预应力钢束分节段张拉。

2 有限元模型

有限单元法是将复杂问题分解为简单问题求解的方法[2]。本工程采用工程设计中常用的MIDASCivil有限元软件进行计算。工程经验证明，该软件模拟地震作用实用性较好。在有限元模型中，主梁，墩柱和桩基承台等构件均采用一般杆系单元来模拟，边跨梁端的边界采用一般支撑模拟支座，桩基与土体之间的作用采用节点弹性支撑模拟，其节点刚度采用“m”法进行计算。

3 静力计算

3.1 节段拼装受力计算

本连续刚构桥梁采用节段悬臂施工，先施工下部桩基承台和墩柱结构，浇筑0号块，张拉预应力束，接着移动施工挂篮，浇筑1号节段，张拉预应力束，以此悬臂施工建立全桥模型，有限元计算模型如下图2所示：

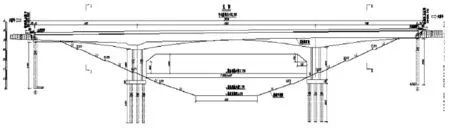
图1 桥梁总体布置立面图（单位：cm）

图2 全桥有限元计算模型

在有限元模型中根据实际情况模拟具体的施工过程，由于本文篇幅限制，故只列出施工过程中受力最不利工况下，即最大悬臂状态下结构的受力状态。其中主梁内力如下表1所示：

最大悬臂状态下，箱梁结构受力最不利位置出现在悬臂根部，其中最大主压应力为10.9MPa，最大主拉应力为1.25MPa，均能满足规范要求，故有限元模型计算是满足要求的。在此基础上提取桥墩的受力状态，由于本桥结构和和荷载均为对称结构，故只提取一个中墩的内力，其轴力，弯矩和剪力如下图3所示：

表1 最大悬臂状态下结构的内力（压为负，拉为正）

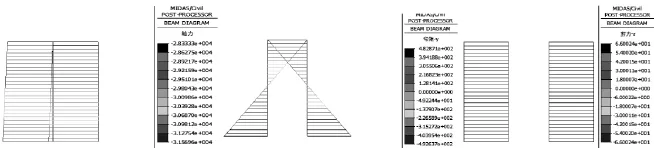
图3 最大悬臂状态下墩柱内力图

从图3可知，在施工过程中墩柱的剪力和弯矩均较小，墩柱受力以受压为主，主要承受上部结构的恒载作用，其轴向压力达到3.16×104kN，截面的最大压应力为4.42MPa，在施工中应力有较高的安全储备。

3.2 成桥状态受力计算

在本桥的施工过程中，上部结构由悬臂状态经过边跨和中跨的合拢，变成连续钢构桥梁，随后在主梁施工铺装等二期恒载，达到成桥状态。由于在施工中箱梁经过悬臂梁变连续梁这一体系转换，结构在成桥阶段的受力也随之变化。列出成桥状态下主梁的内力如表2所示：

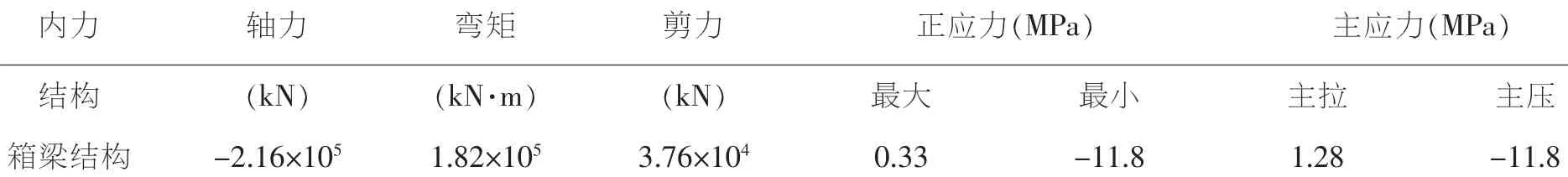
表2 成桥状态下结构的内力（压为负，拉为正）

成桥状态下，箱梁结构受力最不利位置依然出现在悬臂根部，同时在跨中及边跨合拢位置出现局部负弯矩区。主梁最大主压应力为11.8MPa，最大主拉应力为1.28MPa，均能满足规范要求。与最大悬臂状态与成桥阶段受力，成桥状态下的弯矩增大了48%，同时在跨中及变化合拢段范围内出现负弯矩区。但是应力指标并无明显变化，且主梁应力分布更加均匀。同样提取出此受力状态下的桥墩的内力，以此作为后续抗震计算中桥墩的初始受力状态，其内力图如下图4所示：

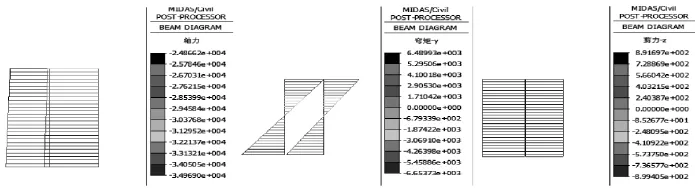
图4 成桥状态下墩柱内力图（力：kN，弯矩：kN·m）

从图4可知，在成桥状态下墩柱的轴向压力为3.50× 104kN，弯矩为6.65×103kN·m，剪力为899kN。相比施工阶段，成桥状态下墩柱的弯矩和剪力均有显著的增大，从图上可以看出，墩柱的正负最大弯矩在墩柱上下两端，其反弯点约在1/2墩高处。上部恒载在成桥状态的增量只是二期恒载和附属等设施，轴向压力变化不是很明显，仅增大了11%，但桥墩结构依然以受压为主。

4 抗震计算

4.1 地震设计参数

该桥梁结构抗震设计采用了二水准设防、二阶段设计的抗震设计思想，第一水准相当于设计地震，第二水准相当于罕遇地震。地震动参数根据专门的《场地地震安全性评价报告》取值。根据该报告，桥址地区地震基本烈度为7度，区域地震动峰值加速度0.10g，地震动反应谱特征周期0.35s，结构阻尼比0.05，地震场地类型为II类。工程设计地震动加速度反应谱根据报告取值。采用多重Ritz向量法进行振型计算和动力分析。

4.2 动力特性分析

在抗震计算前，须先进行结构的动力计算，即特征值分析，为后续抗震计算提供桥梁结构的自振频率等动力特性值。桥梁自振频率能够反映结构整体性能和受力体系特性，是反映桥梁刚度的最直接体现[3]。由结构动力学可知，结构的振动周期、频率等动力特性与结构的质量和刚度分布有关。

在本文有限元模型中，主梁节点个数为110，考虑到X、Y、Z三个方向，模型的振型数达330多个，考虑到桥梁的振型中以低阶为主，在本文计算中仅取前150阶进行计算。其中桥梁的振型参与质量如下表3所示，由于篇幅限制，仅取前5阶及后面每隔20阶的振型参与质量。

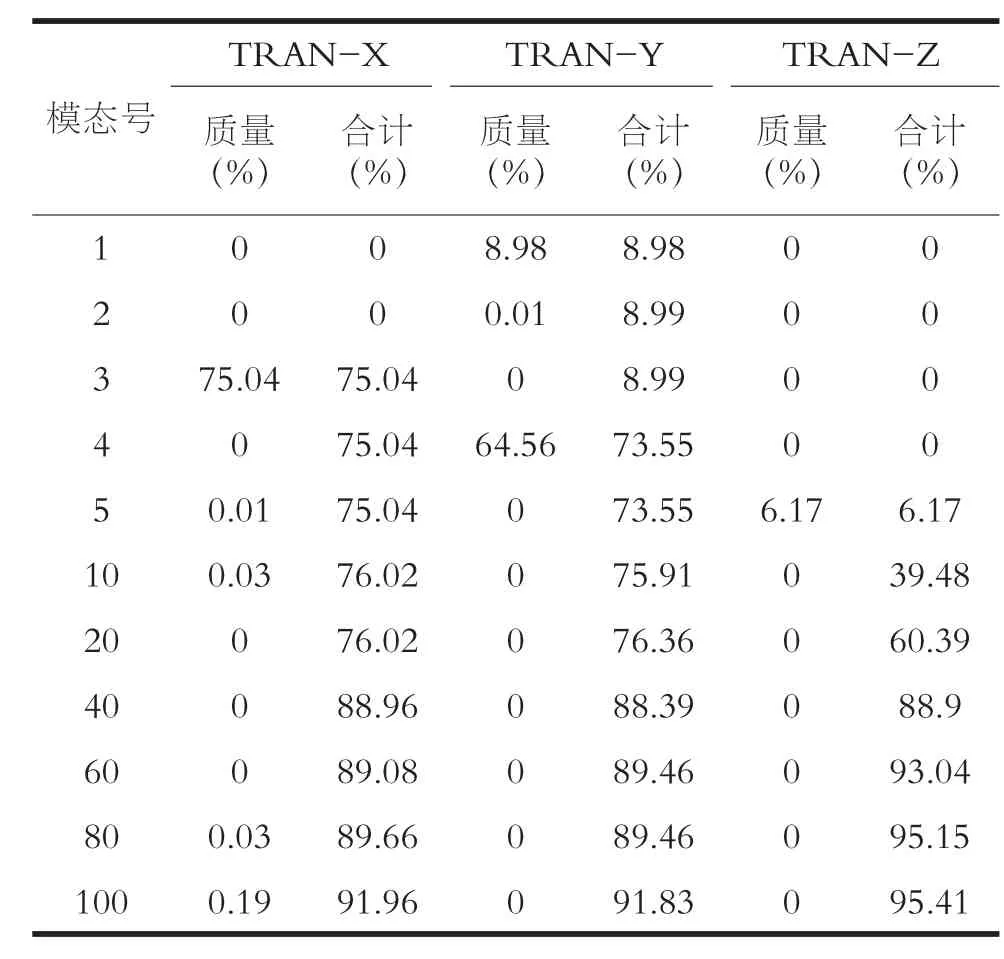
表3 振型参与质量

从上面表格可知，有限元模型在第100阶时，运用里兹向量法求出的X平动、Y平动、Z平动三个方向的振型参与质量分别是91.96%、91.83%、95.41%，均超过了90%，满足规范上振型参与质量达到总质量90%以上的要求。在此基础上，提取有限元分析模型的前5阶动力特性，特性值如表4所示：

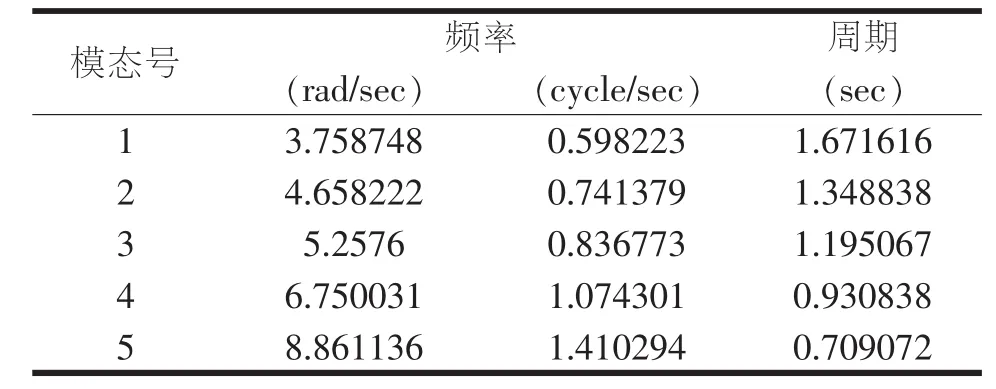
表4 自振频率和周期

从振型方向因子可知，振型1为横桥向的第一阶对称振型，振型2为横桥向的第一阶反对称振型，振型3为顺桥向的第一阶振型，振型4为横桥向的第二阶对称振型，振型5为竖向的第一阶对称振型。

4.3 地震响应分析

地震作用是结构受迫振动的一种形式，结构在受迫振动时的响应与结构自由振动时的频率和振动形式密切相关[1]。本节在动力分析模型的基础上进行抗震设计，地震反应谱按照《公路桥梁抗震设计细则》中相关规定计算，由于本桥类型为B，故要同时验算E1和E2地震作用下结构的响应。应保证在E1地震作用下，结构在弹性范围内工作，基本不损伤，在E2地震作用下，延性构件（墩柱）可发生损伤，产生弹塑性变形，耗散地震能量，但延性构件（墩柱）的塑性铰区域应具有足够的塑性变形能力。

首先进行在E1地震、E2地震作用下的弹性计算，若E2弹性计算不满足，则进行E2地震作用下的弹塑性验算。按弹性计算得出的桥墩最大内力如下表5所示：

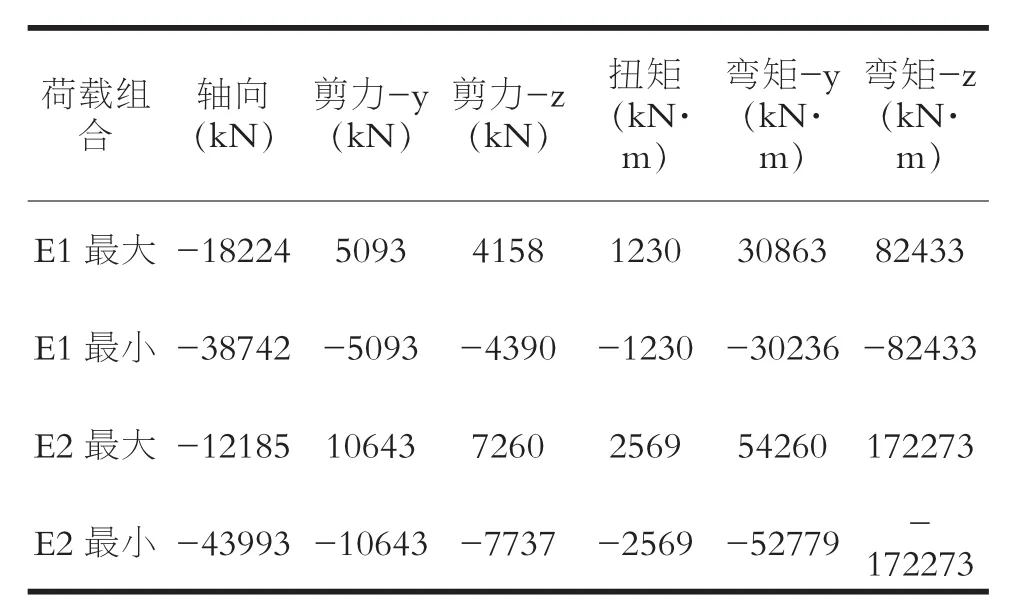
表5 地震工况下墩柱内力最大值

截面屈服弯矩与轴向受力有关，轴力压力越大（压力为负，拉力为正），屈服强度越小。为保守起见，取轴向压力最大时的弯矩-曲率曲线为判断截面是否屈服的标准，如图5：

图5 弯矩-曲率曲线

E1地震作用下，由图5可知，在轴向受压18224kN时，主墩截面顺桥向屈服弯矩为35436kN·m，横桥向屈服弯矩210306kN·m。从表5可知，主墩顺桥向最大弯矩30863kN·m，横桥向最大弯矩82433kN·m，均小于对应主墩截面两个方向屈服弯矩。即可认为在E1地震作用下主墩处于弹性状态，可以按照E1弹性状态对墩柱进行强度验算。

E2地震作用下，由图5可知，在轴向受压12185kN时，主墩截面顺桥向屈服弯矩为32868kN·m，横桥向屈服弯矩为195799kN·m。从表5可知，在E2地震作用下，主墩顺桥向最大弯矩54260kN·m，横桥向最大弯矩172273kN·m，顺桥向最大弯矩大于主墩截面屈服强度，横桥向最大弯矩小于主墩截面屈服强度，即顺桥向部分单元进入弹塑性状态，横桥向可以满足弹性状态。因此，需要按照E2地震弹塑性状态对墩柱进行强度验算，同时对墩柱顺桥向塑性铰区进行抗剪验算，对墩柱顺桥向的塑性转动进行变形验算。

在有限元模型中，运用RC设计对桥梁墩柱进行抗震设计验算可知，墩柱顺桥向的最大正负弯矩位于桥墩墩底和墩顶处，且主墩墩底截面内力大于墩顶，即墩底受力更加不利，故在桥梁设计中应注意对薄弱部位的加强。