基于模糊综合与神经网络的制丝工艺多因素评价模型
2017-07-05王晓娟
王晓娟
(贵州中烟工业有限责任公司贵定卷烟厂,贵州 贵定 551300)
基于模糊综合与神经网络的制丝工艺多因素评价模型
王晓娟
(贵州中烟工业有限责任公司贵定卷烟厂,贵州 贵定 551300)
为解决将制丝工艺质量、设备运行状态、生产消耗作为影响因素联合对制丝工艺进行综合等级判定的问题,建立了基于层次分析法、线性投影法的多因素模糊综合评价模型和神经网络评价模型。通过对甲乙丙3个班组9~12月份质量系数、断料情况等进行建模,表明:神经网络评价模型既可以用于验证多因素模糊综合评价模型的合理性与准确性,也可独立对制丝工艺综合等级进行判定。两种方法相结合,互相验证,为提高制丝工艺综合生产水平提供了科学、简洁的依据,对查找工艺质量、设备运行状态、生产消耗指标下的各项不良因素提供了支持。
制丝工艺;层次分析法;多因素模糊评价模型;隶属函数;神经网络评价模型
制丝过程是稳定产品质量、降低原辅料消耗的重要环节。过程能力指数是指过程能力满足产品质量标准要求的程度,在过程能力判断基准的5个等级中,当过程能力指数处于特级水平(≥1.67)后,可以考虑简化管理、降低成本。目前烟草行业制丝生产设备先进、产品质量稳定,多家卷烟厂正在进行易地技改,因此建立一套制丝工艺综合评价体系显得尤为重要。传统的制丝工艺评价以各工序质量系数为基础,对工艺质量指标和感官质量综合评价与判定,根据结果设置各生产工序适宜的工艺技术参数[1]。2016年新版卷烟工艺规范[2]指出:应定期开展工艺消耗评价,验证工艺消耗控制效果,并结合工艺消耗指标完成情况,对造成物料高耗的工序、流程、操作方法等进行改进。在过程能力指数普遍处于特级水平的前提下,建立基于工艺质量、设备运行状态、生产消耗三者结合的制丝工艺综合评价体系,更符合新形势下的发展需求。目前对制丝过程参数的研究已较为广泛,如刘继辉等[3]应用随机森林回归的方法对制丝过程参数权重进行分析;熊安言等[4]研究了叶丝加料工序工艺参数对加料效果的影响;刘晓龙等[5]运用专家矩阵分析卷烟制造过程特性参数与需求参数之间的关联程度;张涛等[6]研究了制丝工艺参数对9种主流烟气成分释放量的影响。对于成品的综合评价研究也较为成熟,如陶永峰等[7]运用Z比分数与模糊AHP相结合的评价模型,对卷烟成品实验室检测能力进行评价,有较好的应用效果。而直接对制丝工艺综合评价体系的研究则较少,因此建立评价模型对制丝工艺进行综合评价非常必要。多因素模糊综合评价模型用模糊数学对受到多种因素制约的事物或对象作出一个总体的评价,能较好地解决模糊的、难以量化的问题。本试验拟采用多因素模糊综合评价模型对制丝工艺综合评价进行建模。并引入神经网络模型在学习已有评价因素与分数的前提下,预测已知评价因素的综合评价分数并作对比。其最终目的是对不同班组制丝工艺综合评价等级进行对比,不同班组、不同时间的评价等级形成对标,给出影响评价等级的因素,提高工艺质量、设备运行状态、生产消耗影响下的制丝工艺综合生产水平。
1 模型建立
1.1 多因素模糊综合评价模型
对于“制丝工艺综合评价”这一模糊的概念,用精确数学无法准确地界定制丝工艺综合能力属于何种水平,而从模糊数学的观点来看,对于制丝工艺综合评价体系,尽管无法界定它的能力究竟属于哪个级别,但是可以评价制丝工艺综合能力属于某个或某几个级别的程度,这种程度即可量化为隶属度。
在权重的计算过程中,运用了层次分析法[8]对权重进行量化计算。在计算隶属程度时,对原始数据进行无量纲化处理,无量纲化处理采用了基于“线性投影法”的模型,用处理后的数据作为各个因素的评价指标,保证了结果的精确性。
多因素模糊评价方法操作步骤为[9]:
(1) 建立评价对象因素指标集合Z={x1,x2,x3,x4,x5,x6,x7,x8,x9,x10},其中x1~x10对应的因素指标数据为无量纲化后的数据。
(2) 建立待评定对象集合N={N1,N2,N3,N4,N5,N6,N7,N8,N9,N10,N11,N12},数据来自甲乙丙3个班组4个月的生产数据。
(3) 建立评价等级集合P={A,B,C,D,E}。
(4) 建立多因素评价映射体系,即对Z中的每个元素xi,(1≤i≤10),分别建立xi(1≤i≤10)到P的隶属函数映射Fxi,在每个Fxi中,建立单因素评价映射:
f:xij→P∀xij∈xi其中j=1,2,…,10。
(5) 根据即隶属函数,对集合N中的每个班组分别计算多因素模糊判断矩阵RNj(j=1,2,…,10)。
(7) 建立综合评判体系:由于评价对象因素集合Z中各个因素的权重各不相同,利用多层层次分析法逐层计算10种因素的权重集合w={w11,w12,w13,w14,w21,w22,w31,w32,w33,w34},在得出w与RNj的值之后,利用公式:lj=w×RNj计算出综合隶属程度向量lj(j=1,2,…,10)。
(7) 最终将指标集合P中的等级均匀量化,分别给定P中每一个评价指标的量化分值,得到一个量化分值矩阵,记作FP=(P1,P2,P3,P4,P5),则FP×ljT即为最终制丝工艺综合评价分数。
1.2 神经网络评价模型
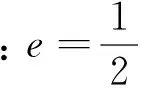

图1 神经网络评价模型算法流程Figure 1 Algorithm process of neural network evaluation model
2 制丝工艺综合评价模型应用
以松散回潮工序质量系数、加料工序质量系数、烘丝及混丝加香工序质量系数、梗加香工序质量系数、断料次数、断料时间等10个主要因素作为评价对象,以2016年制丝车间某A类卷烟9~12月份甲乙丙3个班组的生产数据作为待评定对象。建立5个等级的评语集,对制丝工艺进行综合评价。
2.1 评价指标结构及因素
制丝工艺综合评价指标体系结构见图2。
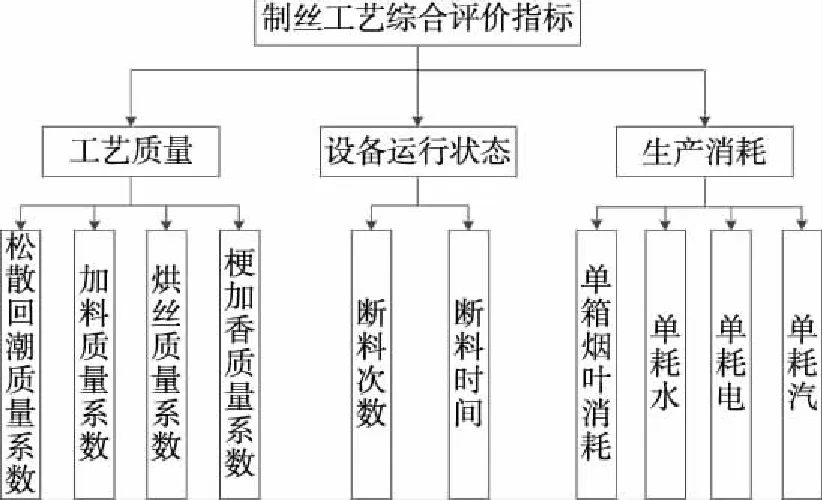
图2 制丝工艺综合评价指标体系Figure 2 Comprehensive evaluation index system of tobacco primary processing line quality
2.2 计算各指标的权重
利用多层层次分析法计算各指标的权重,如w1=(0.636 98,0.104 71,0.258 31)。计算结果通过一致性检验,其余权重见表1。
2.3 “线性投影法”对原始数据无量纲化处理
传统处理方法以理想指标值经无量纲化处理后为“1”,对单向指标进行归“1”化处理。其优点是确保处理后的单向

表1 各指标对应的权重†Table 1 The weight of various indicators
† 目标为制丝工艺综合评价指标,其权重为1。
指标值x∈[0,1],各项指标散布较均匀,综合水平值直观性较好;缺点是理想指标值主观性较大,准确性难以保证。线性投影法是采用一元线性方程将原始数据无量纲化处理的一种方式。本试验采用“线性投影法[12]”:① 使各指标无量纲化处理后的评价标准值在(0,1)范围内,也避免了因指标原始值大小与散布程度使评价结果的失真;② 避免了因选取理想指标值的主观性而造成的误差,使得问题的处理更加准确。
用“线性投影法”对原始数据进行无量纲化处理:将所选取的10项因素原始值在(0,1)区间内投影,采用的线性相对量化数学模型为:
yi=bxi'+c,
(1)
式中:
xi'——各个因素原始值;
yi——投影法处理后的各个因素标准值;
b、c——待定系数。
这里需要引入有关“正指标”“逆指标”的概念,通俗的解释就是:某因素的数值越大,该因素的影响力越强,那么该因素就是“正指标”;如果相反就是“逆指标”。本文所选取的工艺质量因素的松散回潮工序质量系数、加料工序质量系数、烘丝及混丝加香工序质量系数、梗加香工序质量系数4项指标为“正指标”,其余6项指标为“逆指标”。
当x为“正指标”时按式(2)进行具体计算:

(2)
当x为“逆指标”时,按式(3)进行具体计算:

(3)
将所统计的各个因素的数据分别代入式(2)、(3)得到x、y的值,再代入式(1)得到各个因素对应的b、c值,最后通过得到的各个因素不同的b、c值,再分别将数据代回式(1)进行无量纲化处理。
按照上述方法,将10项因素的所有数据无量纲化处理,为了便于后期计算分析,将无量纲化后的数据扩大100倍见表2。
2.4 运用模糊数学原理模型求解制丝工艺综合评价分数



(4)表2 各指标无量纲化扩大100倍数据Table 2 Expanded 100 times of various indicators
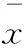
表3 i与si的计算结果汇总表Table 3 The calculation results of i and si
根据模糊数学原理,需要将模糊评价分成多个等级,本试验将评价分成了5个等级,详见表4。
表4 制丝工艺综合评价分数级别定义
Table 4 Scores level definition of tobacco primary processing line quality comprehensive evaluation

级别级别的详细定义级别量化值A制丝工艺综合生产水平优秀,质量水平特级、设备运行状态良好、消耗低90~100B制丝工艺综合生产水平良好,质量水平较高、设备运行状态较好、消耗较低80~89C制丝工艺综合生产水平一般,质量水平有待提高、设备运行无明显故障、消耗较高70~79D制丝工艺综合生产水平合格,质量有不合格情况、设备运行故障较少、消耗高,查找设备故障60~69E制丝工艺综合生产水平不合格,质量水平明显不达标、设备带故障运行、消耗高,不可继续生产0~59

现以x1为例,计算隶属函数Fx1,具体表达式见式(5);对应隶属函数图像见图3。

图3 隶属函数Figure 3 Membership function

(5)
同理可得到剩余9组隶属函数。下面根据已经确定的隶属函数计算隶属度:以x1因素的5个评价等级的隶属度为例,将表2中对应的数值代入隶属函数Fx1中得:

为了方便计算,将计算的数据写成矩阵的形式RN1-RN12:
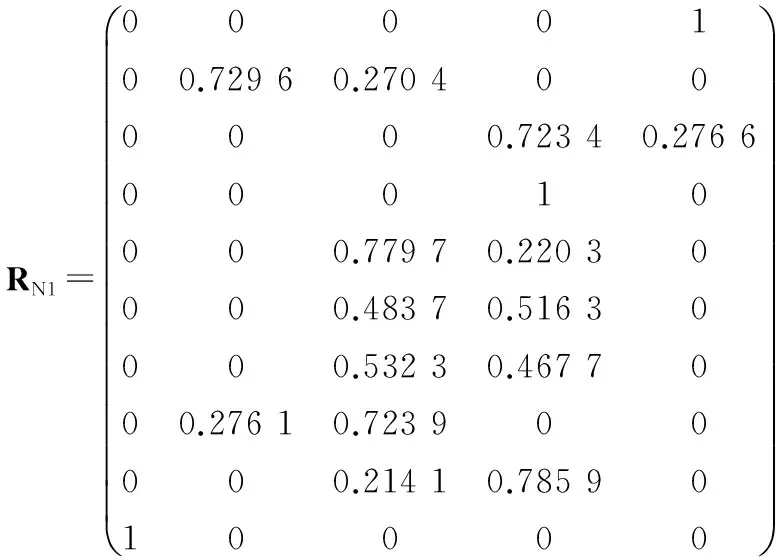



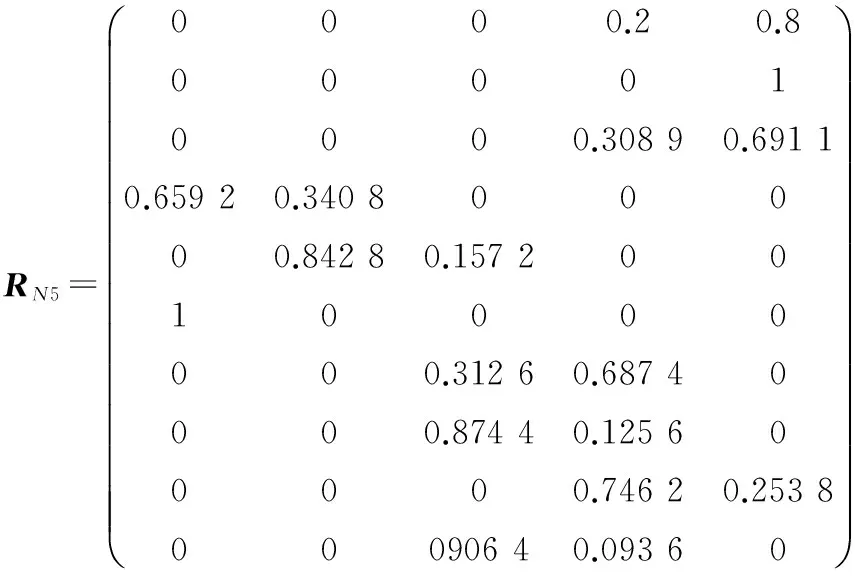

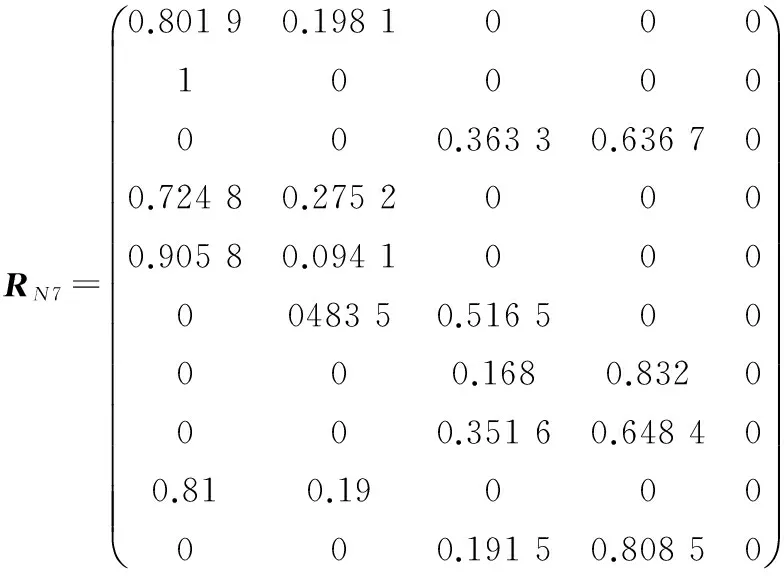

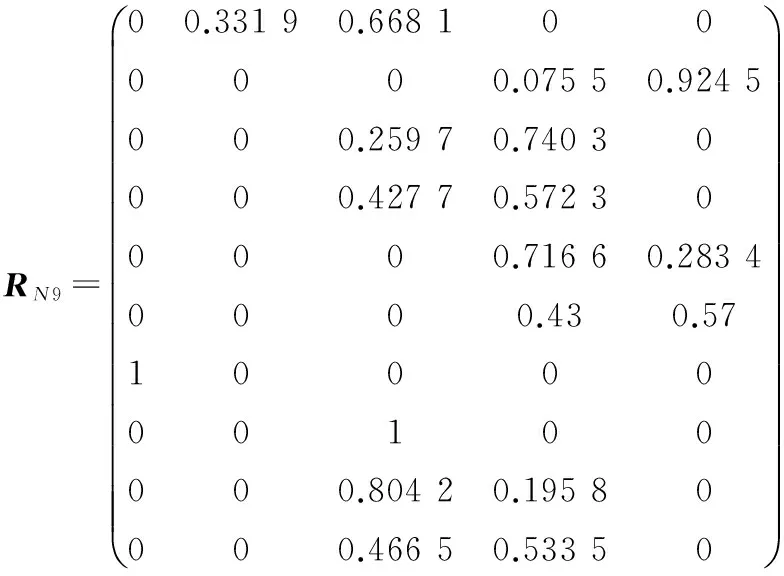



结合数值权重值w计算每个班组的隶属程度向量ln,ln=w×RNn,(n=1,2,…,12)解得l1=(0.032 3 0.086 4 0.211 1 0.476 0 0.194 3),ln详细表示见表5,然后根据表4[级别量化表示为分值矩阵F=(60,70,80,90,100)],计算出F×NiT,(i=1,2,3,4,5)即表示制丝工艺综合评价量化值,结合表4的级别定义,结果详见表6。
2.5 运用神经网络模型求解制丝工艺综合评价分数
首先,将根据甲乙丙3班9~10月份通过多因素模糊综合评价模型计算出的制丝工艺综合评价分数及10个相关因素作为训练集数据,甲班11~12月已知分数及10个相关因素作为测试集数据。然后,依据上述已知条件,运用神经网络评价方法建立数学模型。通过已知的训练集和测试集数据,让数学模型达到自学习的效果,将测试集预测分数误差降至10分以内(见图4)。引入权重的概念,针对不同特征参数进行加权,使自学习数学模型中的测试集预测分数误差降至5分以内。运用建立好的数学模型,已知11~12月份,甲乙丙3班10个相关因素,预测11~12月份甲乙丙三班制丝工艺综合评价分数,最终结果见图5。
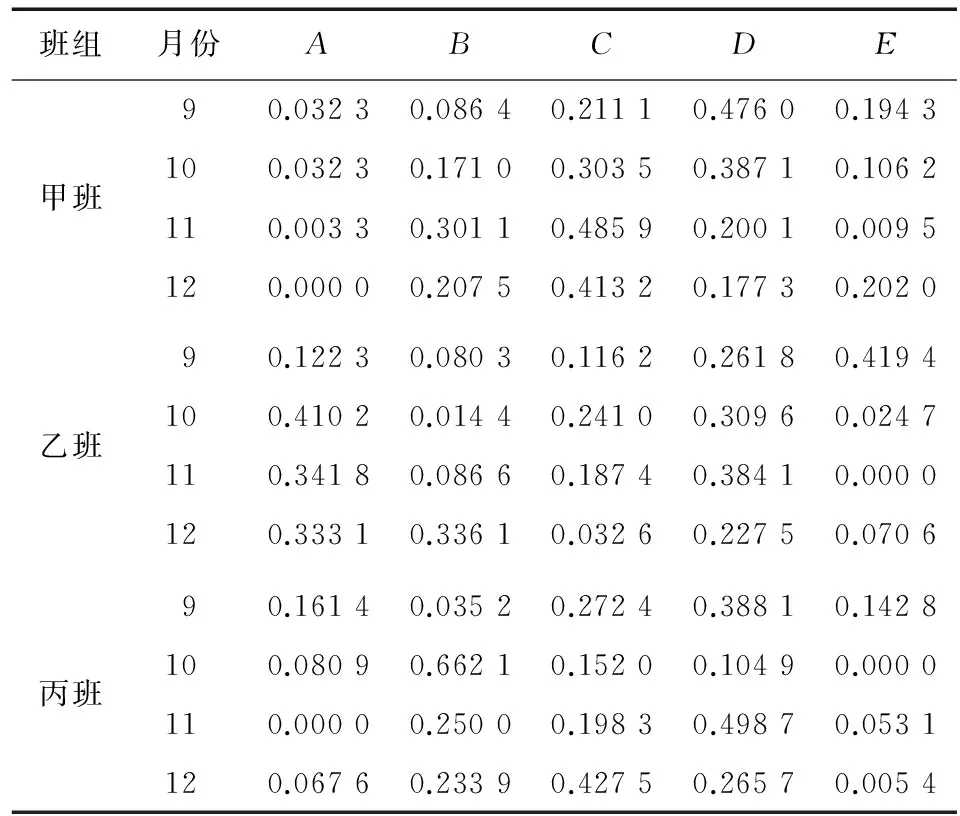
表5 各班组制丝综合工艺评价指标5级隶属度Table 5 Level 5 membership of each team

表6 班组制丝工艺综合评价结果Table 6 The evaluation results of each team
2.6 结果分析
通过多因素模糊综合评价模型与神经网络评价模型计算出的制丝工艺综合评价分数结果见表7。

图4 测试数据预测图Figure 4 Prediction of test data

图5 预测11~12月份甲乙丙3班制丝工艺综合评价分数Figure 5 Prediction score of comprehensive evaluation
通过分析可知,甲班11月份制丝工艺综合生产水平处于B与C级之间,更偏向于C级;甲班12月份制丝工艺综合生产水平处于B级。乙班11月份制丝工艺综合生产水平处于B与C级之间,更偏向于C级;乙班11、12月份制丝工艺综合生产水平处于C级。丙班11月份制丝工艺综合生产水平处于B级;丙班12月份制丝工艺综合生产水平处于B与C级之间,更偏向于C级。而无论是基于多因素模糊综合评价模型还是神经网络评价模型,对制丝工艺综合评价结果的等级相同,则说明多因素模糊综合评价模型用于制丝工艺综合评价可行。通过对制丝工艺综合评价等级的判定,可知3班制丝工艺综合生产能力皆不属于优秀水平,甲班、丙班水平相当,较好于乙班。通过对各因素隶属度矩阵RN1-RN12及表5各班组制丝综合工艺评价指标5级隶属度的数据进行分析可知,乙班11月份松散回潮工序质量系数、加料工序质量系数、梗加香工序质量系数较差,皆属于D、E等级,质量不合格甚至质量水平明显不达标。断料次数属于D、E等级、断料时间属于C、D等级,设备运行状态不佳。乙班12月份各工艺段质量系数皆较差,属于D、E等级,但设备运行状态较好,断料次数与时间较少,消耗水平适中。
3 结论
建立了基于层次分析法、线性投影法的多因素模糊综合评价模型,应用于制丝工艺综合等级评价,最终得到甲乙丙3个班组的制丝工艺综合生产水平及影响其评价等级的不良因素。神经网络评价模型既可以用于验证多因素模糊综合评价模型的合理性与准确性,也可独立对制丝工艺综合等级进行判定。其优点是训练数据越多其准确性越高,减少了权重评价主观因素的作用;其缺点是不能对影响评价等级的不良因素进行判断。因此,当样本数据足够多,并且不需要指出影响评价等级的不良因素时,采用神经网络评价模型准确度更高;但如果需要对影响评价等级的不良因素进行排查时,则多因素模糊综合评价模型的应用更广泛。两种方法相结合,互相验证,对提高制丝工艺综合生产水平提供了科学、简洁的依据,对查找工艺质量、设备运行状态、生产消耗指标下的各项不良因素提供了支持。

表7 班组制丝工艺综合评价结果对比Table 7 The evaluation results comparison of each team
[1] 国家烟草专卖局. 卷烟工艺规范[S]. 北京: 中央文献出版社, 2003: 20-25.
[2] 国家烟草专卖局. 卷烟工艺规范[S]. 北京: 中央文献出版社, 2016: 30-35.
[3] 刘继辉, 许磊, 马晓龙, 等. 基于随机森林回归的制丝过程参数影响权重分析[J]. 烟草科技, 2017, 50(2): 63-71.
[4] 熊安言, 于建春, 王二彬, 等. 叶丝加料工序参数对加料效果的影响[J]. 烟草科技, 2016, 49(1): 66-71.
[5] 刘晓龙. 卷烟制造过程关键质量特性识别及实证研究[D]. 郑州: 郑州大学, 2013: 20-25.
[6] 张涛, 苏明亮, 赵伟, 等. 制丝工艺参数对9种主流烟气成分释放量的影响[J]. 烟草科技, 2014(8):32-37.
[7] 陶永峰, 张胜华, 李文璟, 等.Z比分数-模糊AHP评价模型在卷烟成品实验室检测能力评价中的应用[J]. 烟草科技, 2015, 48(5): 85-89.
[8] 刘璇, 王沛, 毕金峰, 等. 基于层次分析法的晚熟品种苹果脆片品质评价[J]. 食品与机械, 2012, 28(5): 46-50.
[9] 杨纶标, 高英仪. 模糊数学原理及应用[M]. 广州: 华南理工大学出版社出版, 2006: 50-55.
[10] 胡永宏. 综合评价方法[M]. 北京: 科学出版社, 2000: 60-65.
[11] 王小川, 史峰, 郁磊, 等.MATLAB神经网络43个案例分析[M]. 北京: 北京航空航天大学出版社, 2011: 133-137.
[12] 曲玉琨, 张新征, 王章龙, 等. 火炮系统效能综合评价与指标无量纲化处理的研究[J]. 火炮发射与控制学报, 2007(3): 20-20.
Application of fuzzy comprehensive and Neural network evaluation models on tobacco primary processing line quality
WANGXiao-juan
(ChinaTobaccoGuizhouTobaccoIndustiralCo.,Ltd.,Guidingcigarettefactory,Guiding,Guizhou551300,China)
To solve the problems on determining comprehensive level of pipe tobacco technology via pipe tobacco quality, equipment operation and production consumption, the Fuzzy comprehensive and neural network evaluation models were built based on analytic hierarchy process, linear projection method. The modeling results of the three groups based on the mass coefficient and cutting material condition from September to December indicated that neural network evaluation model could not only verify the rationality and accuracy of multi-factor fuzzy comprehensive evaluation model, but also could independently determine the comprehensive level of pipe tobacco technology. It not only offers scientific evidence to improve production levels of pipe tobacco, but also provides support to find negetive factors in process quality, equipment operation and production consumption by combing with the two methods.
Tobacco primary processing line quality; Analytic Hierarchy Process; Multi-factor fuzzy comprehensive evaluation model; Membership; Neural network evaluation model
王晓娟(1973—),女,贵州中烟工业有限责任公司贵定卷烟厂工程师。E-mail:xj0357@sina.com
2017—03—09
10.13652/j.issn.1003-5788.2017.05.041
