剪叉式高空作业平台剪叉臂疲劳寿命分析及预测

潘 权

张 哲1

贺尚红1

刘国良2

(1. 长沙理工大学，湖南 长沙 410114；2. 湖南星邦重工有限公司，湖南 长沙 410600)

剪叉式高空作业平台剪叉臂疲劳寿命分析及预测

潘 权1

张 哲1

贺尚红1

刘国良2

(1. 长沙理工大学，湖南 长沙 410114；2. 湖南星邦重工有限公司，湖南 长沙 410600)

疲劳破坏是剪叉式高空作业平台剪叉臂的主要失效形式之一。用有限元分析软件建立剪叉臂的有限元模型，对其进行静力强度分析，得出剪叉臂在服役中的应力集中区域，再通过设置监测点测试剪叉臂不同位置处的应力状态。结果表明，在剪叉平台开始上升的初始时刻，剪叉臂最大应力发生在靠近油缸支耳下端铰接孔处，说明升降液压缸的驱动力对剪叉臂强度影响很大，且测试结果与仿真结果具有较好的一致性。通过名义应力法并结合材料的疲劳寿命曲线，对剪叉臂结构的疲劳寿命进行预测，为剪叉式高空作业平台的可靠性设计和结构优化提供依据。

疲劳破坏；剪叉臂；名义应力法；疲劳寿命；可靠性设计

剪叉式高空作业平台是一种常用的高空作业专用设备，其主要作用是将工作人员运送到高空进行作业或垂直运送及卸载货物，广泛用于食品加工企业的设备检修及材料运送、建筑、桥梁及公路建设、电力维修、航空航天、船舶制造等领域。剪叉式高空作业平台融入了液压系统、电气系统、安全系统，具有可靠的安全性，且有操作灵活、动力强劲、场地适应性强等优点，适用于室内外、野外或不平工况的场景。其工作过程即在液压缸驱动下剪叉机构伸展和压缩。当剪叉平台处于最低位置时，剪叉机构压缩便于移动和存储；当平台工作时，剪叉机构能快速展开且速度平稳，拥有较高的工作效率[1]。剪叉机构是剪式作业平台的升降执行机构，由两根长度相等、两端通过铰接约束的剪叉臂组成。内外剪叉臂通过中间铰接连接，围绕两臂中点做旋转运动，通过几组内外剪叉臂共同展开使工作平台达到目标位置，完成一个折叠过程[2]。

国内外对剪叉式作业平台的研究主要集中在两个方面：一方面是对剪叉臂在不同铰接方式下的运动特性、力学性能计算仿真的研究。Travis Langbecker[3]通过把剪叉机构几何化，运用数学计算的方法推导了剪叉机构的运动方程，算出了几组不同铰接方式下剪叉机构的具体运动方程，并进行了运动学研究。Zhao Jing-shan等[4]研究了空间式剪叉机构的运动学分析，运用机构分析原理对剪叉臂伸展过程进行定量计算。另一方面是对升降液压缸的最大驱动力、活塞运动速度以及液压缸位置优化的研究。孙东明等[5]分别对单油缸、双油缸、四油缸驱动的升降平台进行了分析，得出了液压举升力与承重之间的关系，并设计了一种合理的液压驱动系统来确保多液压缸驱动情况下工作平台运行的稳定性。邓宏光等[6]研究了剪叉机构的运动特性，对剪叉臂长宽比、厚度及液压缸与水平方向的夹角进行了优化研究。

剪叉臂在工作中主要承受随机疲劳载荷，脉动的疲劳载荷易使剪叉臂结构机械失效，因此其结构强度和疲劳强度对剪叉式升降平台整体性能有较大的影响。本文从剪叉式高空作业平台动力学建模确定升降液压缸推力最大的位置，通过对此状态下的内剪叉臂进行静力学有限元分析，并通过试验验证了计算分析的正确性，最后从疲劳寿命预测角度分析和预测了剪叉式高空作业平台剪叉臂最大易疲劳损伤位置，为其结构设计和优化提供依据。

1 机构运动学分析

1.1 剪叉式高空作业平台工作原理

如图1所示，剪叉式高空作业平台主要由工作平台、延伸平台、升降液压缸、剪叉臂、转动铰链、底盘等零部件组成。从结构上看，升降液压缸两端分别铰接于剪叉臂支耳，内叉和外叉在中点处进行铰接，同时内剪叉臂的一端通过销轴与底盘连接，另一端与上剪叉臂铰接；外剪叉臂一端与底盘的滚动轴滑槽连接，另一端与工作平台铰接。从运动方式看，剪叉式高空作业平通台是过升降液压缸的举升运动转化为滚动轴的横向运动，进一步通过剪叉机构转化为工作平台的竖直运动。

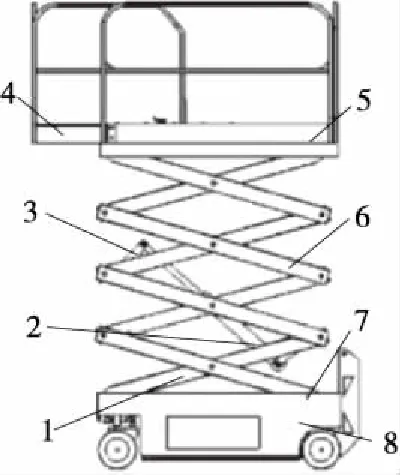
1. 剪叉臂 2. 升降液压缸 3. 液压缸支架 4. 延伸平台 5. 工作平台 6. 伸展结构 7. 转动铰链 8. 底盘

图1 剪叉式高空作业平台结构示意图

Figure 1 Structural schematic diagram of scissors aerial work platform

1.2 运动学及动力学分析

1.2.1 运动学分析 剪叉式高空作业平台具有多种升降液压缸布置形式，针对某型号升降液压缸为两端活动式剪叉平台(见图2)进行运动学分析，确定其升降台特性。

如图2所示，升降液压缸铰接于剪叉臂AC上的Q点，另一端铰接于剪叉臂BD上的P点，根据速度瞬心法有：

vD3=2ω3lcosα3，

(1)

vp=ω3k，

(2)

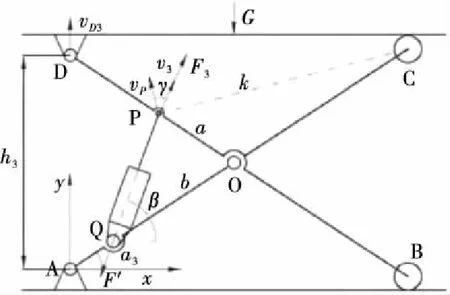
图2 剪叉平台动力学分析模型Figure 2 Dynamic model of scissors work platform

式中：

vD3——升降台的升降速度，m/s；

w3——BD剪叉臂的瞬时角速度，rad/s；

a3——剪叉臂AC与水平面之间的夹角，(°)。

因此：

vp=vD3k/(2lcosα3)。

(3)

可知液压缸活塞运动速度v3的表达式为：

v3=vpcosγ=vD3kcosγ/(2lcosα3)。

(4)

根据三角函数关系及余弦定理有：

cosγ=sin∠QPC=(l+b)sin(β-α3)/k。

(5)

最终可得：

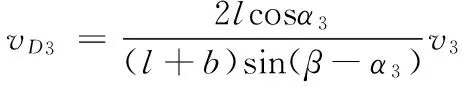
(6)

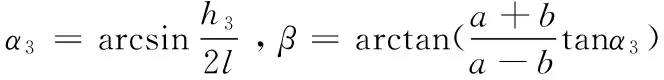
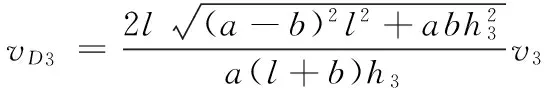
(7)

1.2.2 动力学分析 以A为坐标原点建立坐标系见图2，根据虚位移原理[7-8]有：

∑(Fxiδxi+Fyiδyi+Fziδzi)=0，

(8)

F3cosβδxp+F3sinβδyp-F′cosβδxQ-F′sinβδyQ-GδyD=0，

(9)

式中：

F3——升降液压缸推(拉)力，N；

F′——升降液压缸与剪叉臂AC铰接点Q处对剪叉臂AB的作用力(与F3大小相等，方向相反)，N；

δxQ——Q点沿x方向的虚位移[δxQ=-(l-b)sinα3δα3]，m；

δyQ——Q点沿y方向的虚位移[δyQ=(l-b)cosα3δα3]，m。

可得：

(10)

式(10)变形可得：

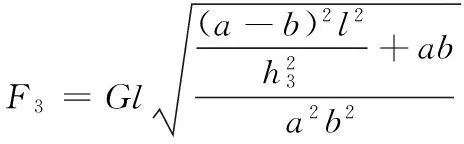
(11)

式中：

a——OP杆的长度，m；

b——OQ杆的长度，m；

l——OA杆的长度，m；

G——额定载荷，kg；

h——高空作业平台上升高度，m。

根据对剪叉式高空作业平台的运动学和动力学分析，利用Origin软件绘制出整个工作平台升程范围内升降液压缸推(拉)力变化曲线(图3)和升降速度变化曲线(图4)。

由图3可知，在剪叉机构负载一定的情况下，升降液压缸推(拉)力F3随着高空作业平台的上升而变小，因此剪叉臂位于最低举升位置时升降液压缸推力最大。由图4可知，升降液压缸的推(拉)力根据F3=mv′，同样是最低举升位置最大而后逐渐变小。

图3 液压缸推(拉)力变化曲线Figure 3 Variational curves of push (pull) force in hydraulic cylinder

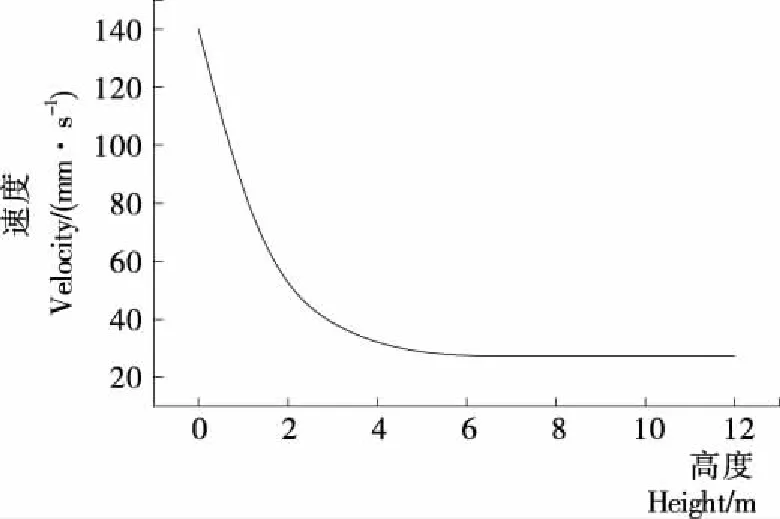
图4 工作平台升降速度变化曲线Figure 4 Variational curves of fluctuation speed for work platform

2 剪叉臂静力学分析

由动力学和运动学分析可知，剪叉臂处于最低举升位置时升降液压缸推力最大，即剪叉平台刚要升起的状态。通过对此状态下的内剪叉臂进行受力分析，得出各铰点的受力情况，用于有限元分析载荷的添加[9]。

利用Solidworks建立高质量的内剪叉臂三维实体模型。内剪叉臂截面形状为长方体钢截面，尺寸为：长2 127 mm，宽80 mm，高120 mm，钢板厚度3 mm。

建立模型后，在solidworks中保存为“x-t”格式，采用ANSYS Workbench有限元分析软件建立剪叉臂有限元单元模型。采用四面体网格进行网格划分[10]，并对接触部位进行网格局部密化处理。网格大小设置为16 mm，得到总单元数为921 971，总节点数1 613 847个。剪叉臂的网格划分见图5。

图5 剪叉臂网格划分Figure 5 Mesh generation of scissors arms

2.1 材料属性设置

剪叉臂材料为Q345，其屈服强度为345 MPa，本研究不涉及传热计算，因此不考虑热膨胀系数和传热系数的影响，在ANSYS/Workbench中对材料属性进行设置(见表1)。

表1 内剪叉臂材料属性Table 1 Material attribute of scissors arms

2.2 载荷和约束施加

剪叉式高空作业平台底盘位于水平地面时，由于剪叉臂位于最低举升位置时升降液压缸推力最大，所以在起升初始位置进行载荷和约束施加。在剪叉臂的两端分别添加圆柱面约束，将各力载荷沿剪叉臂的轴向和法向正交分解，施加在剪叉臂的各交接点，见图6。

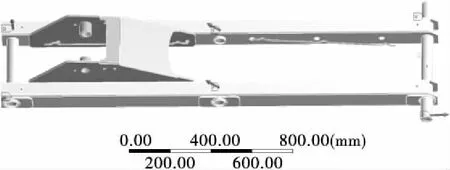
图6 剪叉臂约束加载Figure 6 Defined loads and constraints of scissors arms

挠度根据《起重机设计手册》[11]中对梁刚度的要求，计算得到许用挠度为：

[f]=L/400=2 127/400=5.32 mm。

(12)

式中：

L——剪叉臂的设计总长度，m。

图7为仿真计算的剪叉臂变形和应力云图，内剪叉臂的最大等效应力为286.55 MPa，小于该材料的屈服强度345 MPa，最大挠度为0.846 mm，小于许用挠度值，结构的强度和刚度满足使用要求。由图7(b)可知，由于内剪叉臂受到升降液压缸反作用力的影响，最大应力发生在剪叉臂靠近升降液压缸支腿的铰接孔A的右表面处，中间铰接孔B处上表面也出现应力集中的现象，应力大小为85 MPa，可见升降液压缸的驱动力对剪叉臂的强度影响很大，其他部位应力分布则比较均匀。

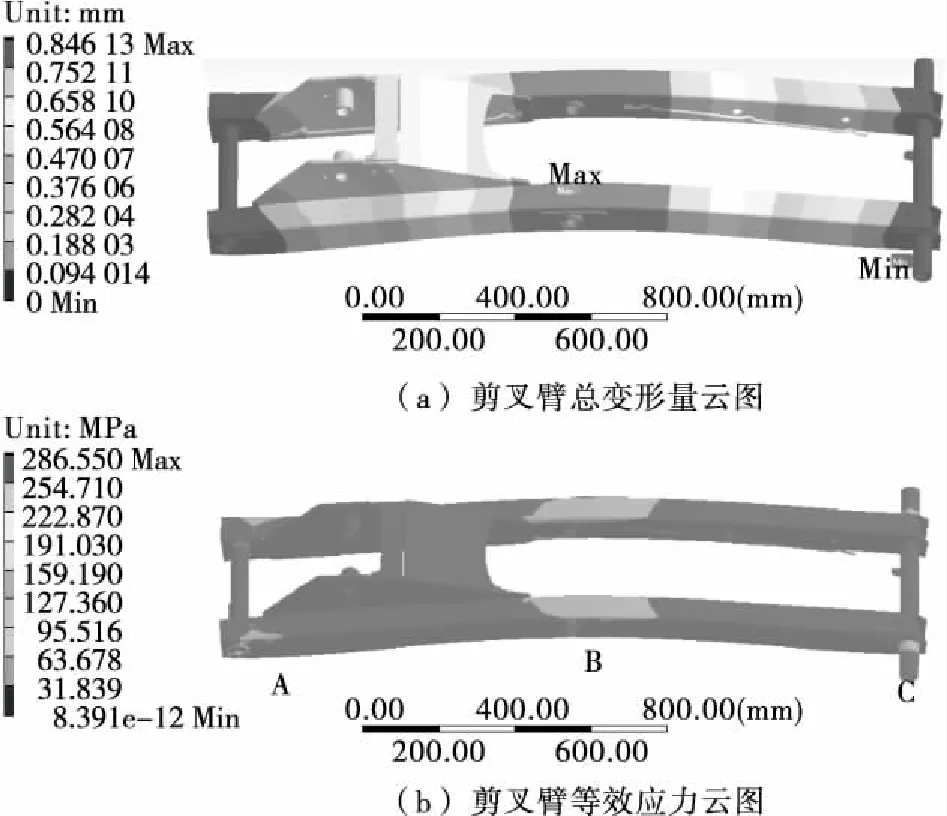
图7 剪叉臂静力学仿真分析结果Figure 7 Static simulation results of scissors arms

3 验证实验

为了验证静力学分析结果的可靠性，对内剪叉臂进行应力分布情况的试验，分别在3个铰接孔处布置4个测量点[12]，试验安装布置见图8。

图8 剪叉臂测试装置Figure 8 Test devices of scissors arms

试实验中用 DH3819无线静态应变测试系统采集数据，每监测点最高采样速度可达1 Hz，其中应变片规格：BE120-3AA(11)-P150，采用公共补偿的方法进行测试。采样时间为1 s，配合各种桥式传感器，对应力信号进行同步采集，自动修正，并实时显示和存储。通过对剪叉式高空作业平台进行两次举升动作，对收集到的数据进行处理，得到各监测点的应力分布图(见图9)。由图9可知，4个监测点的最大应力分别为监测点1：223.13 MPa，监测点2：115.33 MPa，监测点3：115.29 MPa，监测点4：275.36 MPa。内剪叉臂在起升初始位置应力最大，最大应力发生在监测点4的位置，即剪叉式伸展结构最下层靠近升降液压缸支腿的铰接孔A右表面处。仿真结果最大应力发生在剪叉臂的铰接孔A右表面处，最大等效应力为286.55 MPa，试验结果与仿真结果吻合良好。

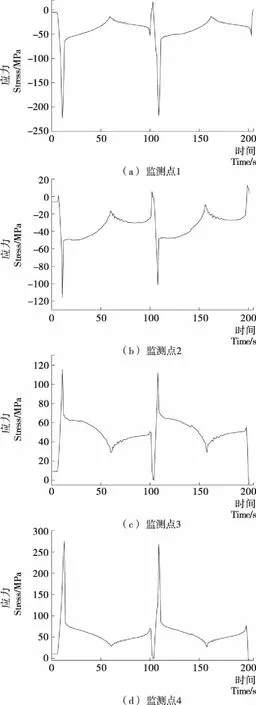
图9 剪叉臂各监测点应力图Figure 9 Stress charts of monitoring points of scissors arms

4 剪叉臂疲劳寿命分析与预测

4.1 剪叉臂疲劳寿命分析方法

零件长时间受到脉动循环载荷的作用，其局部位置的应力仍小于极限强度，但零件的局部会产生疲劳缺陷，局部疲劳缺陷的位置会产生疲劳裂纹并逐渐扩展，直至零件突然失效并发生疲劳破坏[12-13]。运用疲劳分析方法能够预知疲劳缺陷产生的位置，因此该方法也是用来评估零件疲劳寿命的基本方法[14]。目前，通常使用以下几种方法来估算机械零件的剩余疲劳寿命，广泛应用的有：概率疲劳设计法、局部应力应变法、名义应力法以及损伤容限设计法。通过前文对内剪叉臂的有限元分析可知，平台处于最低举升位置时，剪叉臂最大应力值小于其材料的屈服强度，材料属于弹性范围内，因此把内剪叉臂的疲劳问题归属于机械高周疲劳问题，通常选用名义应力法进行疲劳寿命分析。

采用名义应力法进行疲劳寿命预测估算时，以材料和零件的疲劳寿命曲线为估算依据。零件在脉动疲劳载荷下发生疲劳破坏产生裂纹直至零件失效所承受的循环应力次数为零件的疲劳寿命，用N表示。表示应力幅与断裂时的循环次数之间关系的曲线称为疲劳寿命曲线[15]。其表达式为：

NSm=C，

(13)

式中：

S——疲劳应力大小，MPa；

N——零件的疲劳寿命，次数；

m、C——材料常数[16]。

将式(13)两边取对数得：

lgN=lgC-mlgS。

(14)

通过ANSYS Workbench内置的材料属性，可设置内剪叉臂材料的疲劳寿命曲线，见图10。

图10 剪叉臂材料的S—N曲线Figure 10 S—N curves of the materials of scissors arms

当零件承受的应力大于疲劳极限时，每一次循环会产生微量损伤，当损伤叠加超过材料的极限应力，零件会发生破坏。因此还需要运用疲劳累积理论[17]来估算剪叉臂的疲劳寿命。累积理论主要包括3种形式，即Miner理论、Levy理论和Dolan理论。其中Miner理论可以线性地累计损伤结果，可在不同应力下单独进行，具有良好的评估精度，广泛应用于实际工况中。其表达式为：

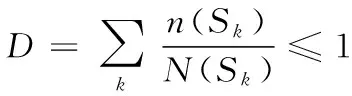
(15)

式中：

D——累积的总损伤；

Sk——对称循环应力，MPa；

n(Sk) ——在该应力作用下的循环次数，次；

N(Sk) ——疲劳寿命，次。

将式(13)代入式(15)得：

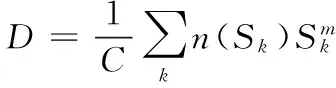
(16)

当式(17)中的D=1时，机构产生疲劳破坏。在安全校核中，通常运用有限元分析来预估算机构的疲劳寿命。

4.2 剪叉臂疲劳寿命影响因素

剪叉臂材料的疲劳寿命曲线数据由各向同性材料试验所得，因此剪叉臂结构的疲劳强度与材料的疲劳强度不同。影响剪叉臂疲劳强度的主要因素包括材料尺寸、应力集中问题、材料表面加工状况(包括表面磨光度、表面粗糙度、表面强化度、表面腐蚀度)、载荷环境(包括载荷类型、频率、峰值)等。在ANSYS/Workbench中可通过设置疲劳强度因子Kf来体现这些因素的影响，设置Kf=0.9。

有平均应力时会产生不对称循环应力，对机构寿命影响很大，因此需对其修正。ANSYS/Workbench可选择修正理论有Goodman、Gerber和Soderberg理论。Goodman理论计算可用于耐久性分析，适用于本文平均应力修正，Goodman直线修正模型将平均应力为σm的循环载荷等效成幅值为σeq的对称循环载荷，其表达式为：

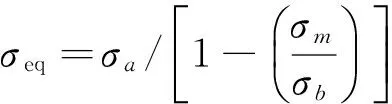
(17)

式中：

σa——应力幅，MPa；

σb——强度极限，MPa。

4.3 剪叉臂疲劳寿命有限元分析

由有限元静力学分析结果可知，在起升初始位置由于升降液压缸的推力作用，此时剪叉臂上应力最大，故对剪式平台起升瞬间进行疲劳寿命分析。平台从最低位置运动到最高位置然后停止，在这个过程中，测试得到剪叉臂各铰接孔表面的应力变化是脉动的，由此设置疲劳载荷为余弦载荷。在ANSYS/Workbench中载荷类型设置成常幅对称循环载荷(Fully Reversed)，见图11。确保驱动系统在正常工况下不发生故障的前提下，剪式平台每日升降次数按50次计算，平台设计寿命设置为20年，该剪叉式高空作业平台的设计寿命为3.65×105次。

4.4 剪叉臂疲劳寿命结果分析

内剪叉臂的寿命云图见图12，数值表示在剪叉臂常幅对称循环载荷作用下发生疲劳损伤所经历的循环次数。由图10可知，其无线循环寿命为1×106次。图12中显示其最大寿命为1×106次，剪叉臂整体都位于蓝色区域，其对应寿命大于3.65×105次，故当前状况下剪叉臂不发生疲劳破坏。图12红色标识处为最大疲劳损伤发生区域，最大疲劳损伤发生在剪叉臂的铰接孔A处的中心轴上安全系数(Safety Factor)云图见图13，安全系数表示剪叉臂的失效应力与设计应力的比值。由图13可知，剪叉臂大部分区域均大于规定的安全系数。安全系数的最小值为0.29，比机械零件常用安全系数(1.5)小，在内剪叉臂铰接孔A附近出现小范围安全系数较小的区域，因此，根据该高空作业平台在实际工作中的情况，可在该位置剪叉臂上焊接加强板进行强化。

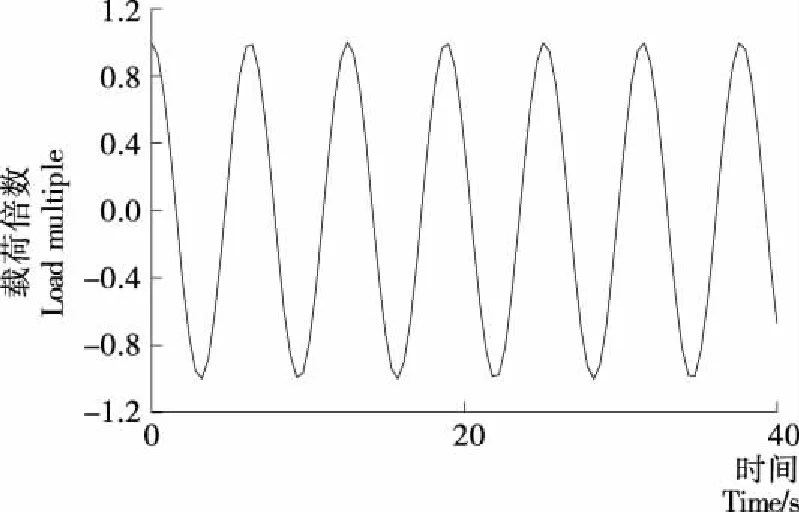
图11 剪叉臂常幅对称循环载荷曲线Figure 11 Constant-amplitude cyclic loading curves of scissors arms

图12 剪叉臂寿命云图Figure 12 Life nephogram of scissors arms

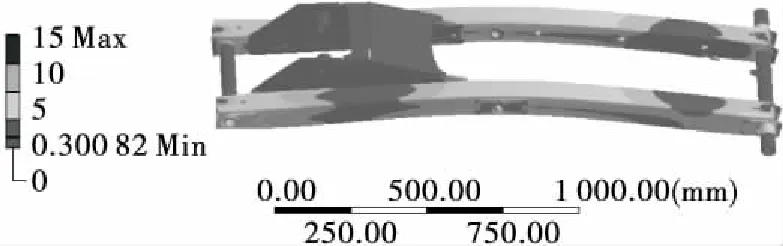
图13 剪叉臂安全系数云图Figure 13 Safety factor nephogram of scissors arms

5 结论

(1) 剪叉式高空作业平台剪叉臂位于最低举升位置时升降液压缸推力最大，升降液压缸推力随工作平台的上升而变小并逐渐趋于平稳。

(2) 在剪叉平台开始上升的初始时刻，剪叉臂最大应力发生在靠近油缸支耳下端铰接孔处，说明升降液压缸的驱动力对剪叉臂强度影响很大。仿真计算得到的剪叉臂应力分布情况与试验结果吻合良好。

(3) 疲劳仿真计算得出剪叉臂最大应力位置发生疲劳损伤最大，损伤区域为内剪叉臂与底盘铰接的铰接孔处。可

在该位置剪叉臂上焊接加强板进行强化。

[1] 殷彬. 剪叉式机动平台的设计与结构优化[D]. 长沙: 长沙理工大学, 2012: 1-4.

[2] 孙光旭, 袁端才. 液压剪叉式升降台的动力学仿真[J]. 系统仿真学报, 2010, 22(11): 2 650-2 651.

[3] TRAUIS Langbecker. Kinematic Analysis of Deployable Scissor Structures[J]. International Journal of Space Structures, 1999, 14(1): 1-15.

[4] ZHAO Jing-shan, CHU Fu-lei, FENG Zhi-jing. The Mechanism Theory and Application of Deployable Structure Based on SLE[J]. Mechanism and Machine Theory, 2009, 44(2): 324-335.

[5] 孙东明, 董为民, 李珊. 对称驱动的重载剪式升降平台的设计[J]. 机械设计与制造, 2006(6): 23-24.

[6] 邓宏光. 剪叉式升降平台建模及关键参数研究[J]. 机电工程技术, 2005, 34(7): 20-22.

[7] 丁智平. 气液动剪叉式升降平台运动受力分析及其应用[J]. 株洲工学院学报, 1999, 13(16): 49-52.

[8] 倪素环, 张弛. 一种新型液压升降台的研制[J]. 工程机械, 2011, 42(1): 59-61.

[9] 熊顺源, 鲍卫宁. 空气悬架C形托架的疲劳寿命设计[J]. 机械制造, 2008, 46(12): 21-23.

[10] 蒋红旗. 高空作业车作业臂有限元结构分析[J]. 机械研究与应用, 2004, 17(6): 68-69.

[11] 张质文, 虞和谦, 王全诺. 起重机设计手册[M]. 北京: 中国铁道出版社, 2001: 59-62.

[12] 赵宁, 董金善, 杨云雨. 椭圆封头大开孔补强有限元分析及试验研究[J]. 食品与机械, 2016, 32(4): 103-105.

[13] 姚卫星. 结构疲劳寿命分析[M]. 北京: 国防工业出版社, 2003: 63-70.

[14] 王国军. MSC Fatigue 疲劳分析实例教程[M]. 北京: 机械工业出版社, 2009: 42-44.

[15] JOOSTEN M W. New study shows how to predict accumulated drill pipe fatigue[J]. World Oil, 1985(10): 21-25.

[16] 徐才发, 李伟. 起重机主梁舱门处开裂的故障分析[J]. 起重运输机械, 2000(9): 32-35.

[17] 曾春华, 邹十践. 疲劳分析方法与应用[M]. 北京: 国防工业出版社, 1991: 11.

Fatigue Life Analysis and Forecast of Scissors Arms in Scissors Aerial Work Platform

PANQuan1

ZHANGZhe1

HEShang-hong1

LIUGuo-liang2

(1.ChangshaUniversityofScienceandTechnology,Changsha,Hunan410114,China;2.HunanSinoboomCo.,LTD,Changsha,Hunan410600,China)

Fatigue destruction is the main way for scissors arms to lose effectiveness in the scissors aerial work platform in the actual situation. Through finite element modeling of scissors arms established by ANSYS and static strength analysis, the region of stress concentration of scissors arms has been concluded. Stress condition of different locations in scissors structure has been found by setting monitoring sites. It has been showed that the stress condition of the initial position of scissors arms is the biggest, and the maximum stress location lies in the hinge hole of legs of lifting cylinder at the bottom of the scissors arms, which indicates the driving force of lifting cylinder has a great impact on the intensity of scissors arms. Moreover, the test results are in accord with the stimulation result. Using nominal stress method, fatigue life analysis of scissors arms in scissors aerial work platform in ANSYS, the fatigue life can be predicted, which will provide the reliability design and structure perfection of scissors aerial work platform with proof and evidence. The fact that the fatigue life of scissors arms can be predicted by using nominal stress method and fatigue life curves of scissors arms in scissors aerial work platform, provides proof and evidence for the reliability design and structure optimization of scissors aerial work platform.

Fatigue destruction; Scissors arms; Nominal stress method; Fatigue life; Reliability design

国家自然科学基金项目(编号：51275059)；湖南省自然科学基金项目(编号：2015JJ4003)

潘权，男，长沙理工大学讲师，博士。

贺尚红(1965—)，男，长沙理工大学教授，博士生导师，博士。E-mail:heshanghong@126.com

2017—04—06

10.13652/j.issn.1003-5788.2017.05.025