电力系统短期负荷预测

蒋年子 张 鹤 肖 迪 朱家明

(1.安徽财经大学统计与应用数学学院 安徽蚌埠 233000； 2.安徽财经大学金融学院 安徽蚌埠 233000)



电力系统短期负荷预测

蒋年子1张 鹤2肖 迪1朱家明1

(1.安徽财经大学统计与应用数学学院 安徽蚌埠 233000； 2.安徽财经大学金融学院 安徽蚌埠 233000)

针对给定的地区一的电力负荷和气象情况的历史数据，首先进行对数据的初步分析，得到各个统计量分布数据。接着综合地区一的气象因素，建立基于分形理论的负荷水平预测构建模型，把短期负荷预测的过程分为曲线模式、负荷水平两部分进行，构造出迭代函数系统，拟合出预测的负荷曲线，然后利用负荷量与气象因子的拟合函数求出气温敏感度，考虑因温差变化对负荷水平的影响，经过负荷还原，得到预测日的负荷水平的具体值。

电力负荷预测； 气象因素； 分形理论； EVIEWS

0 引言

电力负荷预测和负荷特性分析是电力管理部门的重要工作，是电力市场环境下作出调度和交易计划的前提和基础，其预测精度是否达标关系整个电力系统的效率、效益和安全性。电力负荷预测总共有两层含义：一方面是用在国家机关、企业公司、住户等各用电器械设备，另一方面是用以描述用电器械设备所消耗的电力电量。在电力负荷预测中，很多因素不同程度地影响着电力荷的预测值，比如自然变化的气象因素。

1 数据来源

数据来源于第九届中国电机工程学会杯全国大学生电工数学建模数据，包含地区一的电力负荷和气象情况数据。

2 统计指标分析

整理地区一2014年每天96个数据，求出最大值、最小值、极差，分别对应日最高负荷、日最低负荷、日峰谷差，日负荷率的公式为：

日负荷率=日负荷量的平均值/日负荷量的最大值*100%

利用处理后的数据在EVIEWS中作出地区一分布折线图，见图1。

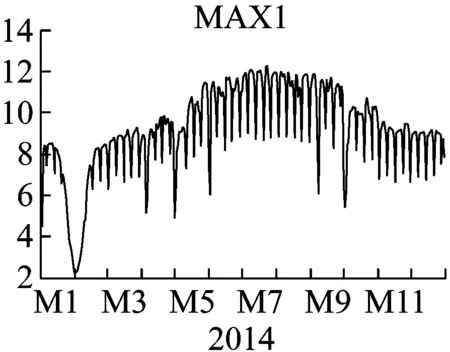
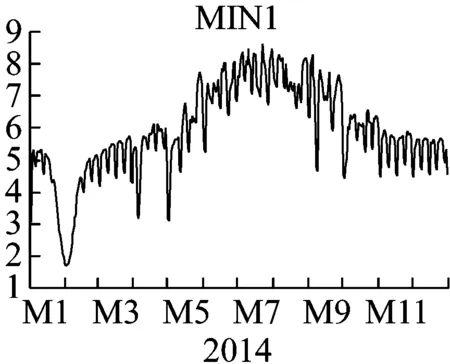
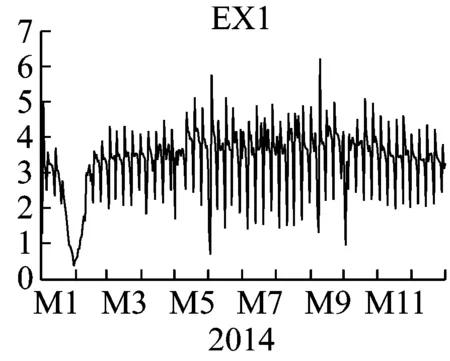
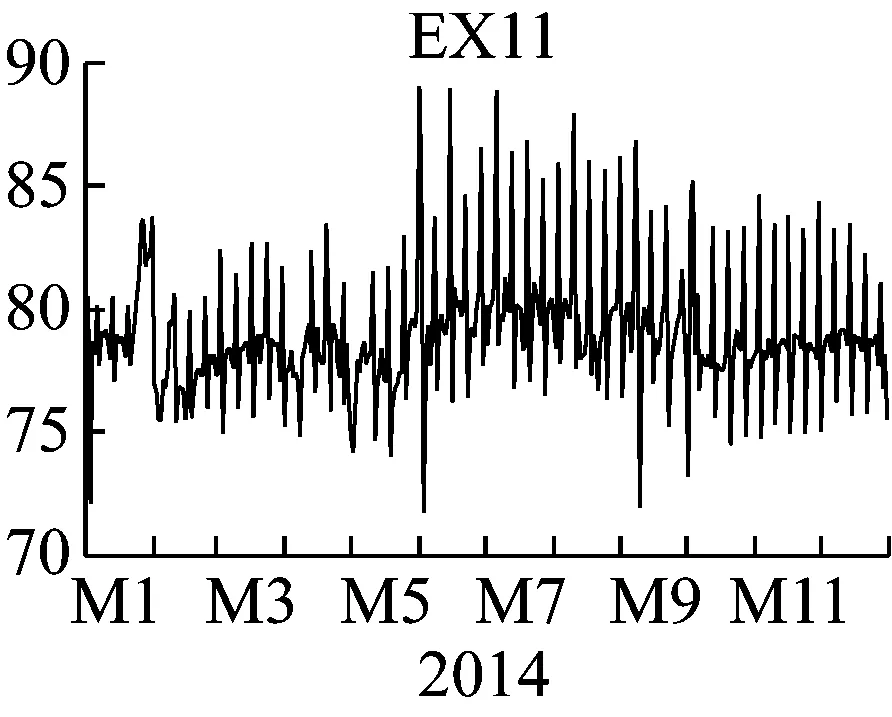
图1 地区一日最高负荷、最低负荷、峰谷差、负荷率

其中，MAX1代表地区一日最高负荷，MIN1代表日最低负荷，EX1代表日峰谷差，EX11代表日负荷率。通过观察图1可得，地区一基本在一月至二月的用电负荷达到最低值，后趋于上升，在七八月份达到最大值，后逐渐下降，在十二月至一月达到另一个小高峰。与现代用电情况基本吻合，在天气较热时，电力负荷大幅增大，而在天气较温和时期，用电负荷较低。而在一月至二月达到最低点，可以推测是由于天气寒冷并且处于年假期间。具体地区一的分布图的参数，均值、最值、标准差等参数值见图2。

由图2可看到地区一日最高负荷的均值是9 222.652，中间值是9 155.296，最大值是12 296.85，最小值是2 242.059，标准差是2 074.834，偏度系数是-0.994 433，峰度系数是4.293 490，JB统计量是86.603 24。同时，其他几个负荷量指标也可从图2中得到。

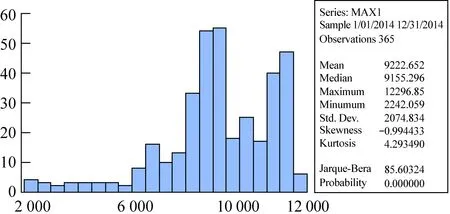
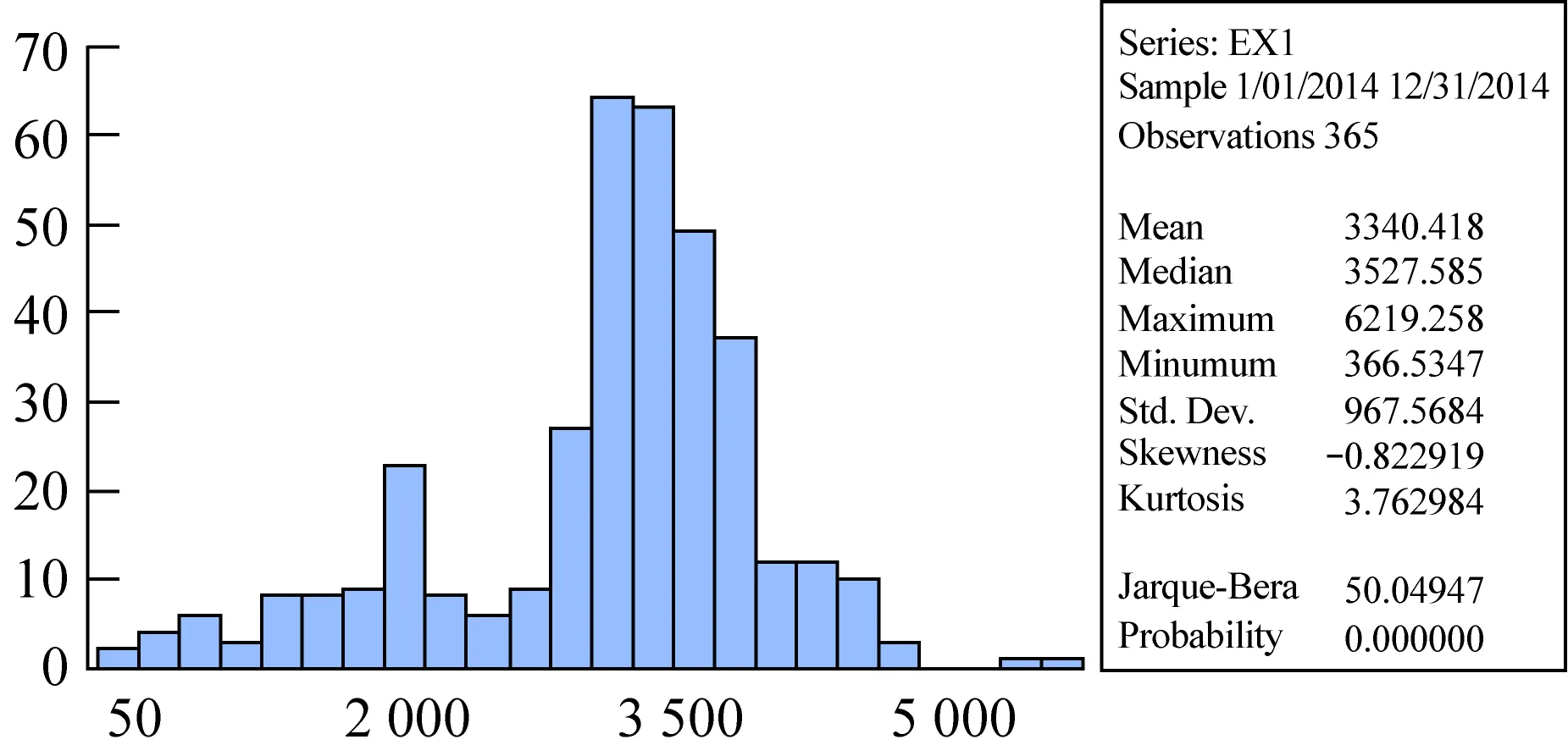
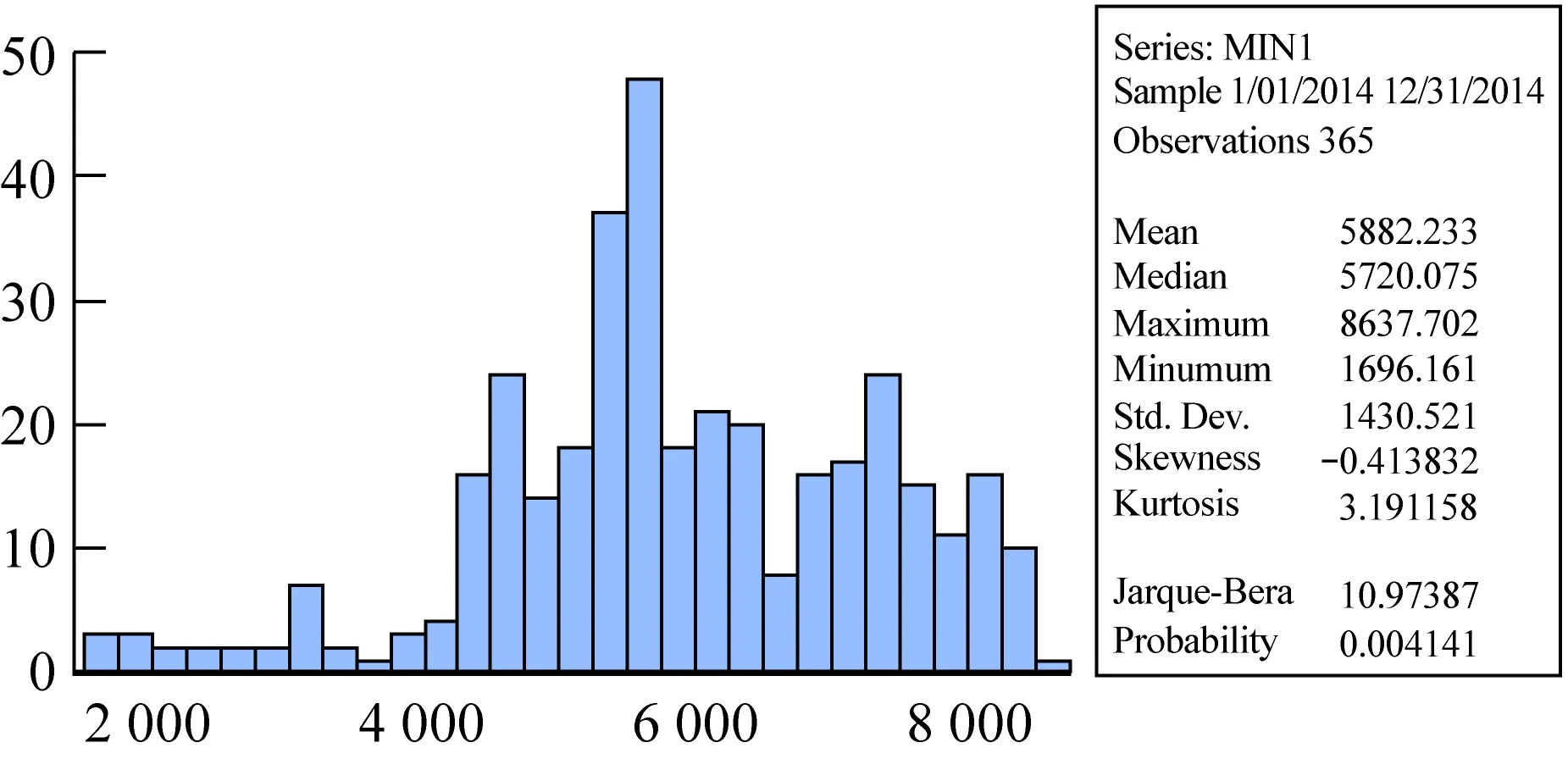
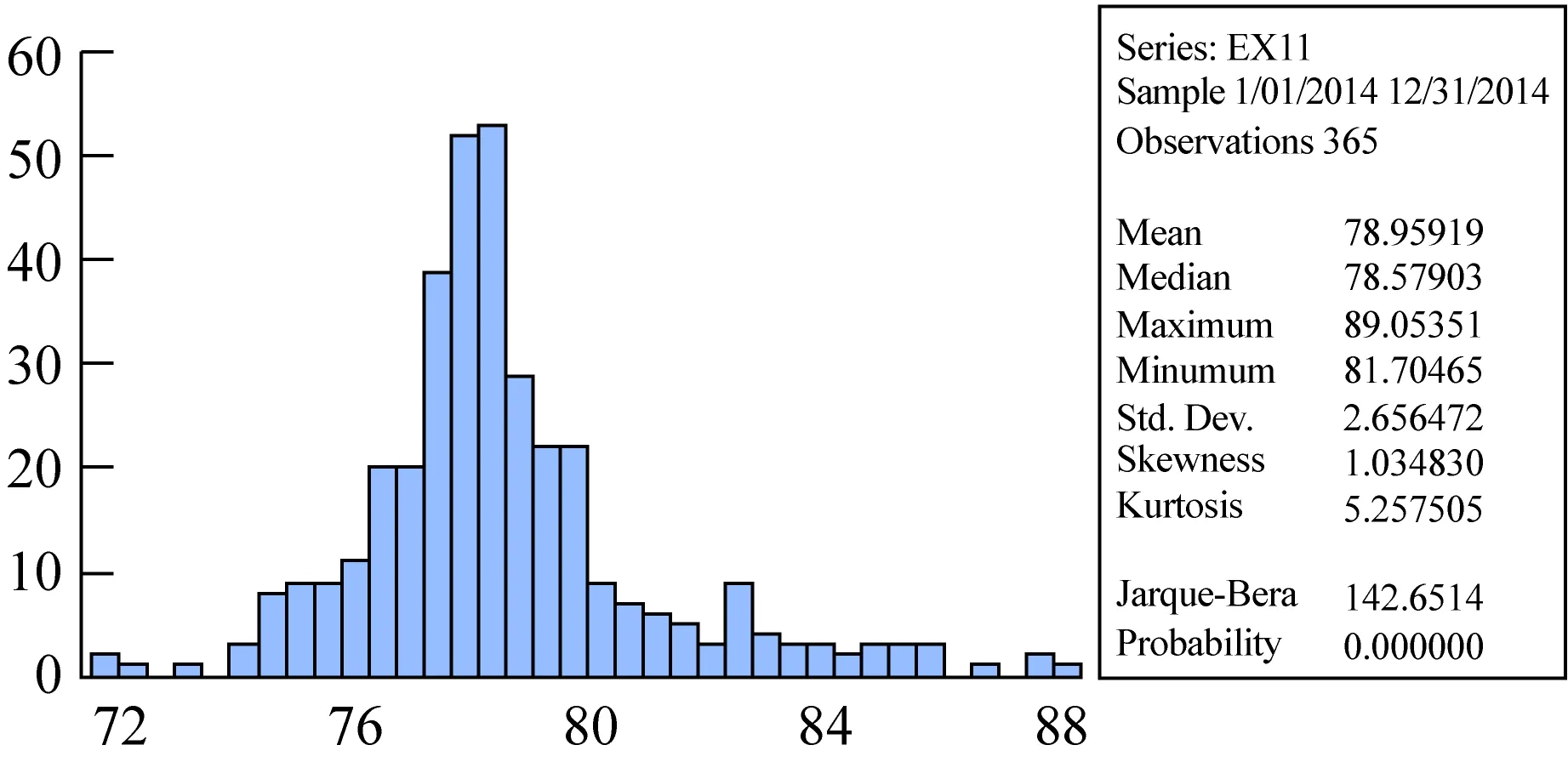
图2 地区一各统计指标值

3 短期电力预测

考虑气象因素，为更加准确预测地区一2015年1月11日—1月17日共7天的短期电力负荷，综合考虑多种因素，把短期负荷预测的过程分为曲线模式、负荷水平两部分进行。首先选取相似日或典型日作为参考对象，以此考虑气象因素对预测日负荷的影响，由分形插值方法对负荷曲线模式进行预测。然后，对负荷与气象各个因素之间进行内在关联性分析，对负荷水平作出估计，最终还原并计算最终电力负荷预测值[1]。

3.1 模型准备

电力负荷曲线图是凹凸、粗糙、不光滑且不平稳的几何形体，在描述这一几何形体时，传统的数学方法存在较大难度，本文考虑利用分形理论。分形理论[2]是一门分线性系统理论，分形理论认为，分形内部任何一个相对独立的部分，在一定程度上都应是整体的再现和缩影。现进行负荷预测基于分形理论的可行性分析，分形具有以下四个典型特征[3]：

1) 分形具有更加精细的结构，应对于电力负荷量每时每刻都在变化。

2) 分形是完全不规则的，因此无论整体还是局部都无法用具体的几何曲线来描述，应对于电力负荷数据具有某种混沌无序性，即使在非常小的时间间隔里，也是毫无规律可循的。运用普通插值法得到的拟合曲线相对光滑，当然也只是对实际情况的一种虚拟。

3) 分形的维数大于它的拓扑维数，而电力负荷实际维度是多维，负荷曲线的拓扑维度是一维。

4) 分形通常有某种自相似的形式，而电力负荷每时每刻都是具有一定的自相关性。

由上面的分析，可以得到电力负荷具有周期性、自相似性与标度不变形的特征，与分形理论的前提相符合。为了得到具体的负荷水平数据，首先进行负荷模式预测，利用分形插值算法，根据历史负荷数据来构造迭代函数系统(IFS)，接着拟合待预测的电力日负荷曲线。然后是电力负荷水平预测，通过建立气温与负荷的回归模型，以求得电力负荷对气温改变的灵敏度，然后根据参照电力日负荷和待预测日与参照日的气温差值来求解待预测的电力日负荷水平。

3.2 模型建立

首先根据已有的数据，利用插值方法构造迭代函数系统，{R2,wi,i=1, 2,…,n}将使其吸引子趋近于分形插值函数f(x)的图像。这个迭代函数系统中，每个函数wi都是仿射变换，其构造形式为：

式中，(x,y)为某一点的坐标；ai、ci、di为变换矩阵元素；ei、fi为(x,y)变换后的常数分量。满足如下条件：

这样就可以确定IFS中的第i个仿射变换wi。在求得IFS参数后，就可采用确定型的迭代算法得到IFS的吸引子。迭代次数逐渐增加时，由插值算法得到的曲线与原来曲线的拟合程度将会不断提高，经多次迭代之后就可以得到稳定的插值曲线[4]。

3.3 模型求解

考虑不同时间段时负荷组成与特性变化，本文将待预测日的电力负荷曲线分不同时段来预测，然后对每一段曲线分别采用分形插值方法进行曲线拟合，其中第n段的预测步骤如下[1]：

1) 将一些突出的点剔除，或是补上缺失的点，进行负荷数据预处理。

2) 以待预测日为初始点，向前按顺序选取k个同样类型的历史日为训练样本，每个样本的大小为t。也就是选取了2014—2012年的1月11日—1月17日的数据，k=3，t=96。

3) 并对每个样本进行数据规格化处理：yi=(Yi-Ymin)/(Ymax-Ymin)(i=1，2，…，96)。

4) d值(垂直比例因子)的选取：di=(yi-yi-i)/(ymax-ymin)(i=1，2，…，96)。

5) 构造迭代函数系统：由3)中数据规格化处理公式后，对每个规格化后的样本都可以构造一个IFS。具体系数可由下式求得：

ai=(xi-xi-1)/(xn-x0)

ei=(xixi-1-x0xi)/(xn-x0)

6) 预测负荷曲线：对已经求解得到的三个迭代函数系统进行加权平均，求得一个统计意义上的IFS。为了更加合理地得到权重系数，本文基于已求得3个迭代函数系统，建立了迭代函数系统的自适应滤波模型[1]，流程图见图3。

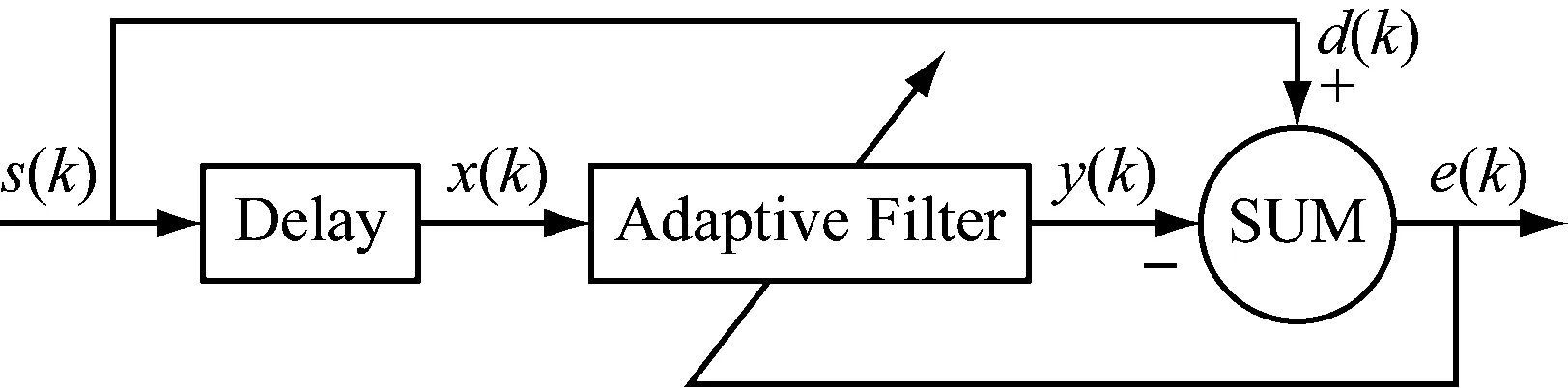
图3 自适应滤波模型预测流程图

7) 负荷水平预测。

首先经分析得到负荷水平和气象因子的相关程度，见表1。选取最大负荷量和日最高温度进行二次拟合，拟合方程是：

MAX=8.996T2-257.32T+8 934.03

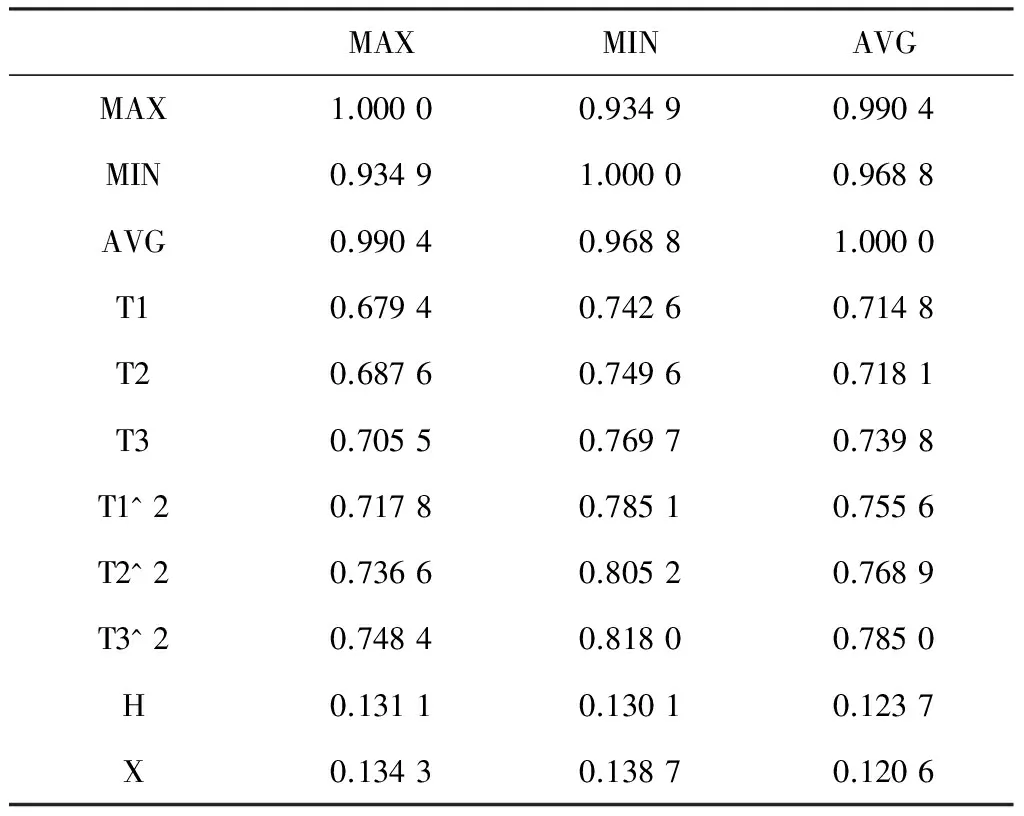
表1 各解释变量相关系数表

然后利用拟合方程中极值负荷对气温求导，ST=dMAX/dT=17.992T-257.32求出不同气温区间下负荷对气温变化的敏感度，见表2。

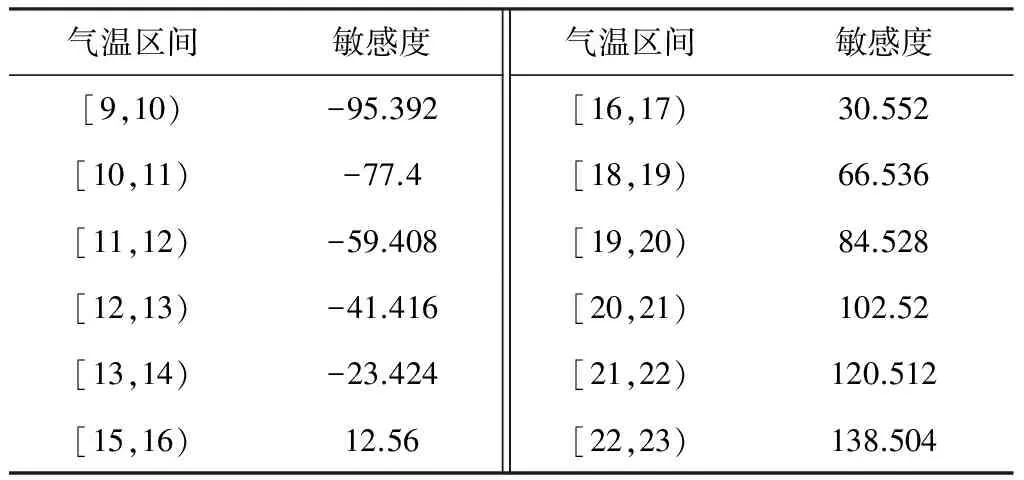
表2 负荷对气温变化的敏感度取值

选取恰当的参照日，根据待预测日与参照日的温度差值来修正：L=L′+ΔL。式中：L为待预测日的极值负荷，L′为参照日的极值负荷，ΔL为由于气温变化因素而引起的负荷变化量ΔL=St(t-t′)，St为电力负荷对气温变化的敏感程度。

8) 负荷还原：结合6)中计算得到的待预测日负荷曲线形状与7)得到的负荷最值得预测值，利用公式：Yc=yc(Yf max-Yf min)+Yf min。式中：Yf max和Yfmin分别为待预测日负荷最大值和最小值的预测值[5-6]。参考负荷趋势的转折变化，将日96个四分之一刻钟电力负荷分为如下4段：凌晨时段(1—25时刻)、早高峰时段(26—50时刻)、午高峰时段(51—74时刻)和晚高峰时段(75—96时刻)。按照以上方法得到地区一在2015年1月11日—2015年1月17日这七天电力负荷预测，见图4。

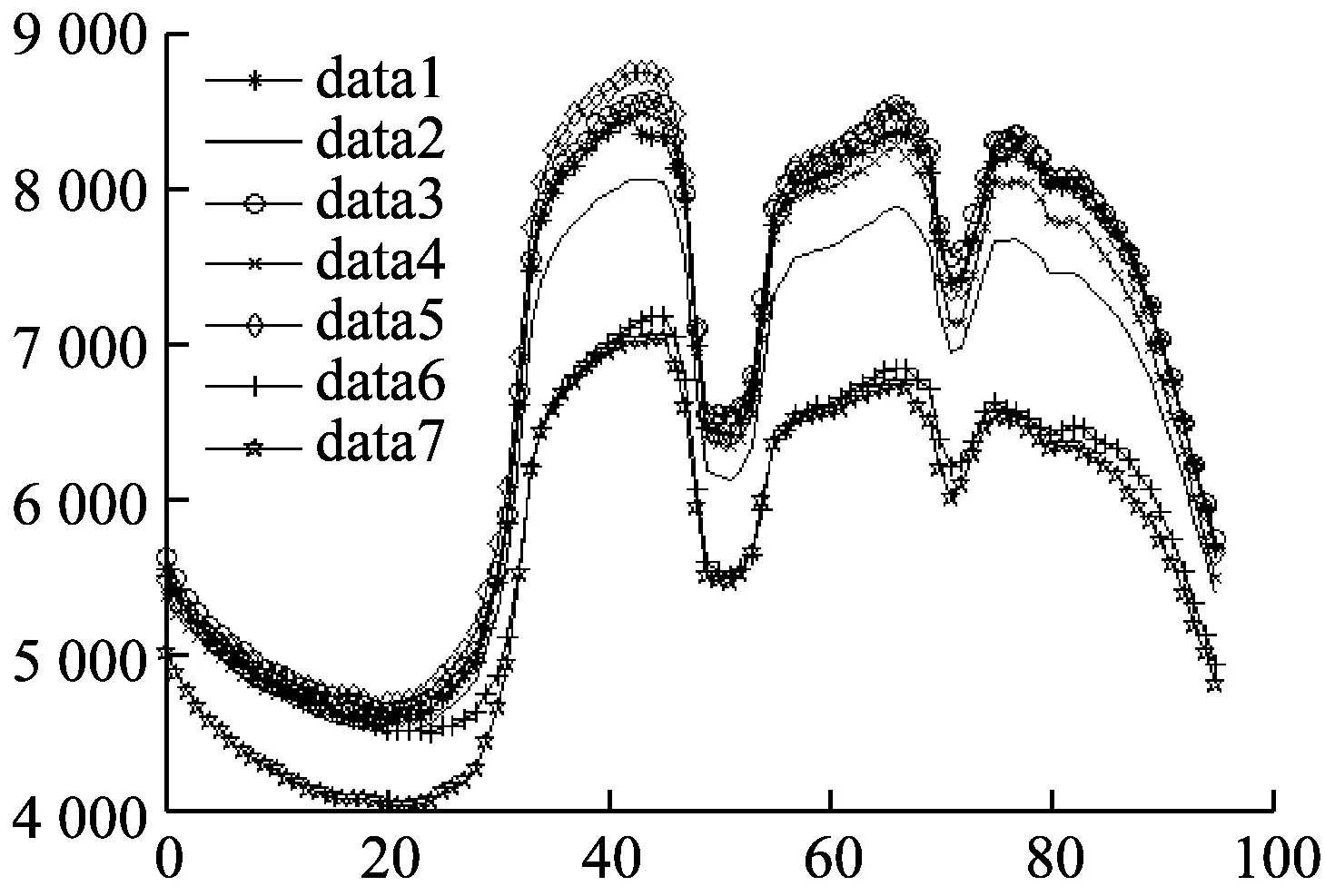
图4 地区一负荷水平预测趋势图

4 结果分析

在进行对电力负荷水平的预测时，不同的气象因素对其影响的程度也是千差万别，因此对电力负荷的预测需考虑气象因素。实际情况表明，气象因素是对电力负荷影响最为显著的。例如，在天气极热的夏天时，使得大量制冷的设备运作，比平时有更大的电力负荷；在天气极寒的冬天时，将会有大量的制暖设备进行运作，这也比平时增加电力负荷；同时降雨也会存在一定影响。本文需要预测一月中七天的数据，由于温度或冷或暖、降雨与否，都会对用电负荷产生较大的影响。

[1] 李小燕.考虑气象因素的电力系统短期负荷预测研究[D].广州：华南理工大学，2013：37-44.

[2] 肖瑶.基于分形理论的电力短期负荷预测研究[D].长沙：中南大学，2007：33-46.

[3] 徐云燕.基于基因表达式编程的电力负荷预测算法[J].计算机与现代化，2012(2)：19-25.

[4] 王伟.基于混合核函数支持向量机的电力负荷预测[J].现代计算机，2013(4)：22-25.

[5] 张志向.厦门翔安电力负荷管理系统的规划研究[D].昆明：云南大学，2012：5-20.

[6] 杨桂元.数学建模[M].上海：上海财经大学出版社，2015：185-209.

[责任编辑：李娟]

Short-term Load Forecasting of Power System

JIANG Nianzi1ZHANG He2XIAO Di1ZHU Jiaming1

(1. School of Statistics and Applied Mathematics， Anhui University of Finance and Economies, Bengbu 233000, China;2. School of Finance， Anhui University of Finance and Economies， Bengbu 233000, China)

According to the historical data of power load and meteorological condition in a given area, the data are analyzed firstly, and the distribution data of each statistic is obtained. Then, based on the meteorological factors of a region, the load level prediction model is established based on the fractal theory, and the short-term load forecasting process is divided into two parts: the curve mode and the load level. To construct iterated function system, fitting curve forecasting, and then we use the fitting function of meteorological parameters and load derived temperature sensitivity to temperature changes due to the impact of load level is taken into account. After the load reduction, we get the specific value of the load forecast finally.

power load forecasting; meteorological factors; fractal theory; EVIEWS

2017-04-21

国家自然科学基金(11601001)

蒋年子(1996-)，女，主要研究方向：统计学

TM 744

A

1672-2434(2017)03-0012-04