纤维尺寸对漂白硫酸盐木浆悬浮液屈服应力的影响
2017-07-05郑学梅沙九龙程金兰
王 晨, 郑学梅, 张 辉, 沙九龙, 程金兰
(1.南京林业大学 江苏省制浆造纸科学与技术重点实验室,江苏 南京 210037; 2.南京林业大学 江苏省林业资源高效加工利用协同创新中心,江苏 南京 210037)
纤维尺寸对漂白硫酸盐木浆悬浮液屈服应力的影响
王 晨, 郑学梅, 张 辉*, 沙九龙, 程金兰
(1.南京林业大学 江苏省制浆造纸科学与技术重点实验室,江苏 南京 210037; 2.南京林业大学 江苏省林业资源高效加工利用协同创新中心,江苏 南京 210037)

WANG Chen
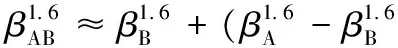
漂白硫酸盐木浆;纤维悬浮液;屈服应力;集聚因子
纤维悬浮液广泛存在于制浆造纸、食品、聚合物及生物产品等化学工业领域之中[1],在一定质量分数下纤维缠绕交织所形成的网络结构使得悬浮液表现为非牛顿流体,需要受到一定的应力作用才能呈现出屈服效应而流动起来,因此屈服应力是其重要的流变性能参数之一。而对于与国民经济发展和社会生活需要有着密切联系的制浆造纸工业而言[2],纸浆纤维悬浮液的屈服应力的研究,可以为浆料的输送、搅拌、混合、中高浓浆泵、高速纸机流浆箱等制浆造纸工艺及机械设备的设计与优化提供理论依据[3]。已有纸浆纤维悬浮液屈服应力的研究主要着眼于屈服应力与质量分数之间的关系[4-5],而纤维尺寸对屈服应力影响的研究还相对较少[6-7],对于两者之间的关系还缺乏深入的认识。在实际生产过程中常将纤维尺寸不同的浆料混合后抄造,因此浆料混合后对屈服应力的影响也需要进一步开展相关工作。基于此,本研究采用硫酸盐法蒸煮并漂白的针叶木和阔叶木浆板为原料,分别分析了这两种浆料的纤维尺寸在相同质量分数和集聚因子范围内对屈服应力的影响,并改变两种浆料的质量比,探讨了混合浆料的纤维尺寸对屈服应力的影响。
1 实 验
1.1 材料与仪器
硫酸盐漂白针叶木浆板(银星)和硫酸盐漂白阔叶木浆板(森博)。
电子天平,量程120 g,精度0.000 1 g;纤维形态分析仪Morfi (TECHPAP France),长度测量范围0.2~10 mm,宽度测量范围5~75 μm;流变仪Brookfield (MA USA),采用桨式转子,4叶片,叶片宽度为20 mm,高度为80 mm,外部槽体内径为120 mm,剪切力控制范围0.7~420 Pa,剪切速率控制范围0~306 s-1。
1.2 纤维悬浮液配制
遵照国家标准GB/T 462—1989测定两种浆板的干度,以确定其中的绝干浆含量,其中针叶材浆板干度为92.38%,阔叶材浆板干度为92.35%。而后依据3组实验中各实验样本中绝干浆质量,换算得到各样本所需浆板质量。表1和表2所示为各实验样本的质量分数或集聚因子,及对应的浆板质量。配制样本时称取相应质量的浆板在装有900 mL去离子水的容积为1 L的玻璃烧杯中浸泡24 h,之后用疏解机疏解10 min使浆料分散,再加入去离子水配制成质量为1 kg符合要求的实验样本。
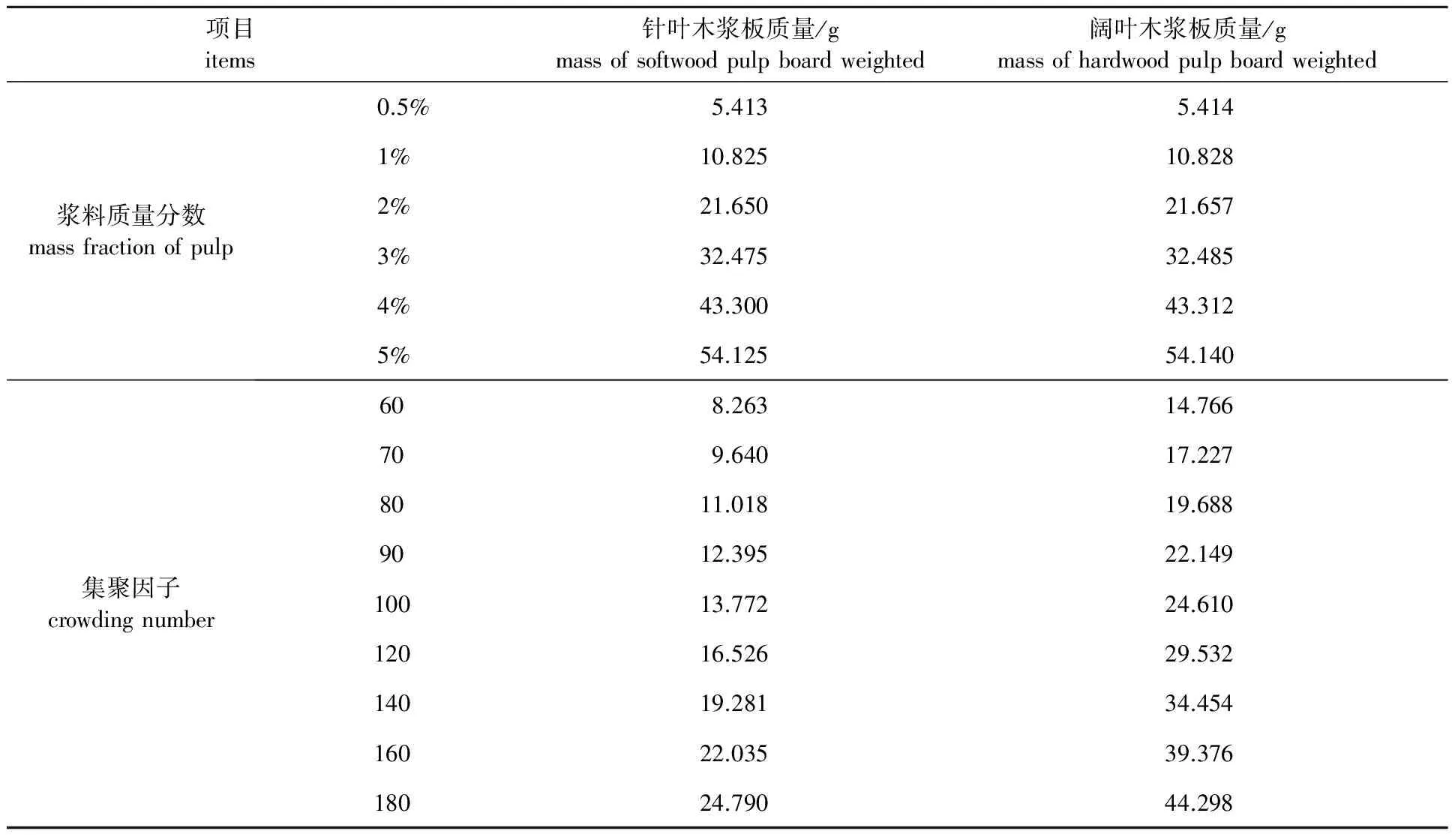
表1 单一浆料样本中所需浆板质量
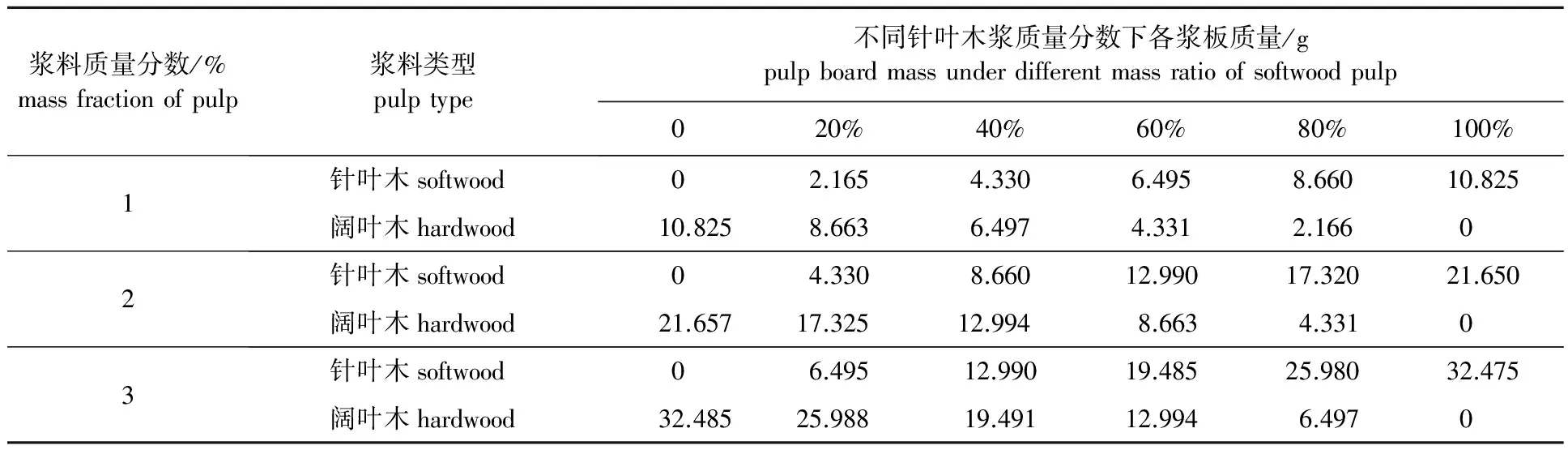
表2 混合浆料各样本中所需浆板质量
1.3 屈服应力测量
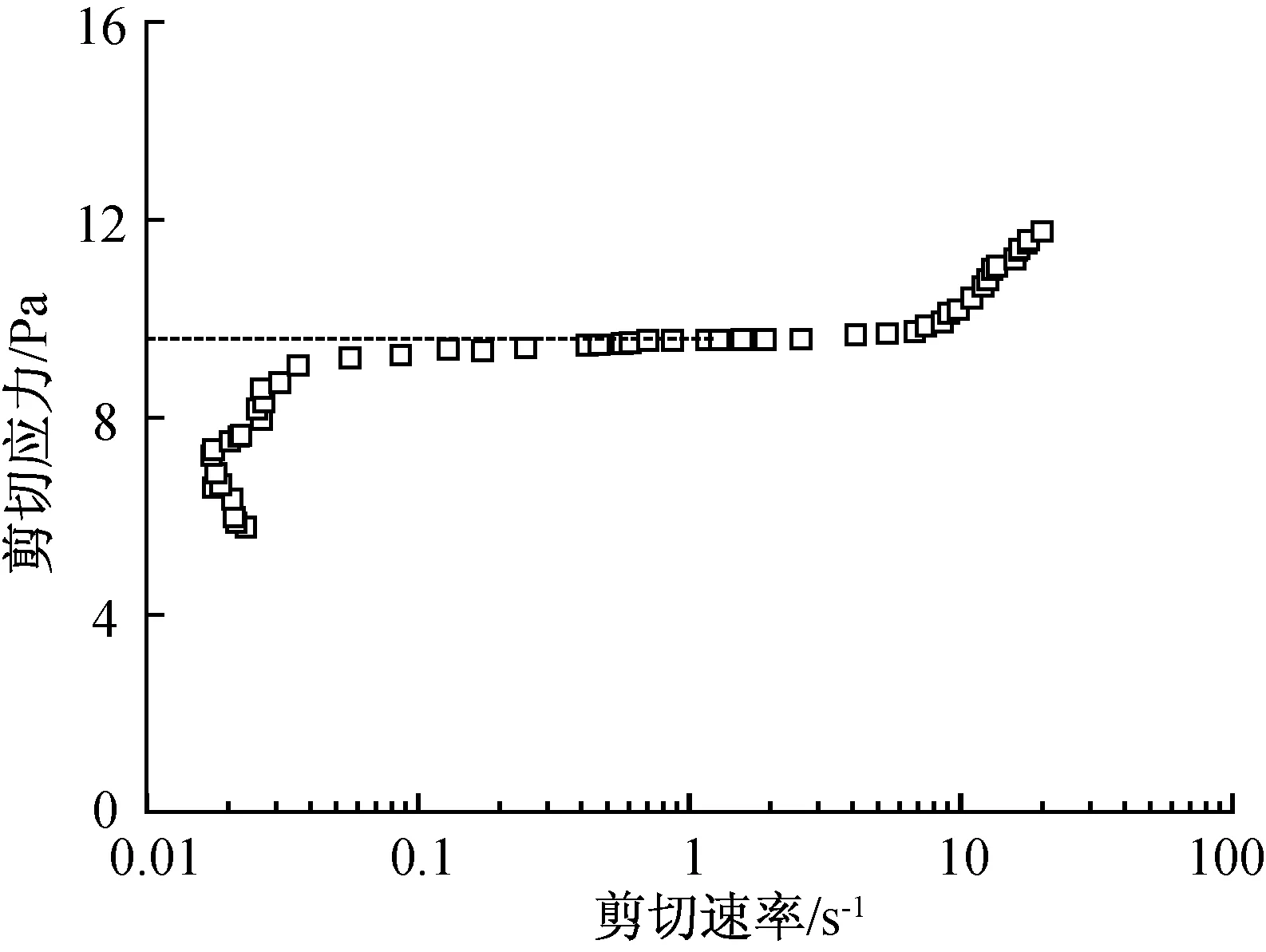
图1 质量分数为1%的针叶木悬浮液的流变曲线Fig.1 Flow curves of softwood pulp with 1% concentration
将配制好的纤维悬浮液实验样本倒入流变仪测量槽内,移动流变仪转子下降直至其完全没入样本液面以下,通过流变仪自带程序设定其自动工作步骤。为了保证初始条件一致,每一个的实验样本在测试前由程序控制转子对其进行剪切速率200 s-1下预剪切3 min,再静置5 min后开始测量。
测量时,在控制剪切应力模式下,使剪切应力由较小的初始值逐步增加到某一值,在此过程中流变仪测量并记录浆料的剪切应力随剪切速率的变化曲线,当在对数坐标体系下剪切速率曲线出现明显的应力平台,如图1所示,即转子发生初始转动时对应的剪切应力即为浆料悬浮液的屈服应力[8]。所有测试过程均维持在室温20 ℃下进行。同一实验条件进行3次平行实验。
2 结果与分析
2.1 浆料纤维性能分析
由纤维形态分析仪测量得到的针叶木和阔叶木浆料纤维长度分布如表3所示,两种浆料的长度分布均符合正态分布规律。两种浆料及混合浆料纤维平均尺寸如表4所示。可以看出,随着针叶木浆料质量的增加,混合浆料的纤维平均长度和平均粗度都呈现出上升的趋势。
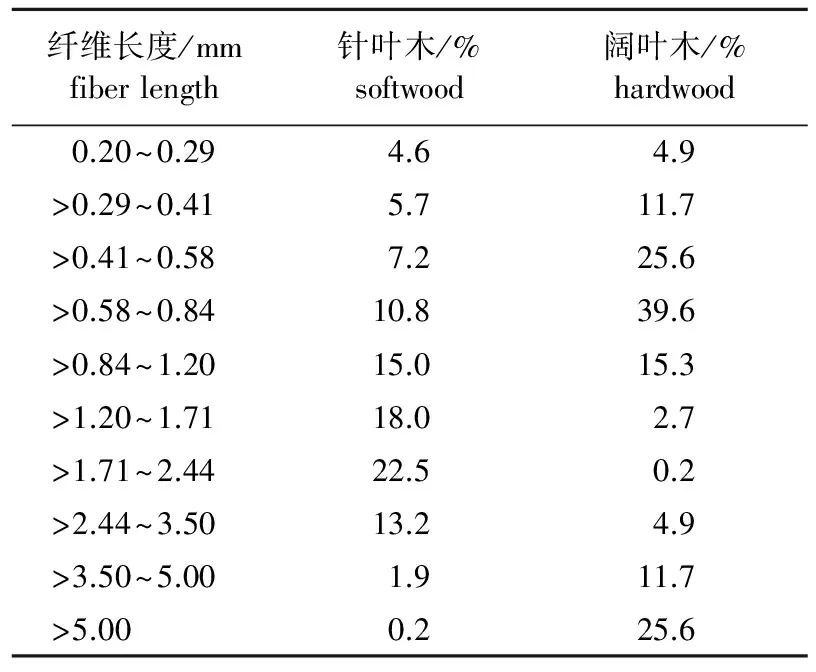
表3 两种浆料的纤维长度分布
2.2 单一浆料纤维尺寸对屈服应力的影响
2.2.1 相同质量分数范围内的屈服应力 大多数文献均表明屈服应力(τy)与质量分数(Cm)之间呈幂率关系[9-10],见式(1):
(1)
式中:τy—屈服应力,N;Cm—质量分数,%;a,b—与纸浆纤维特性相关的常数。
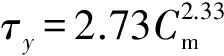
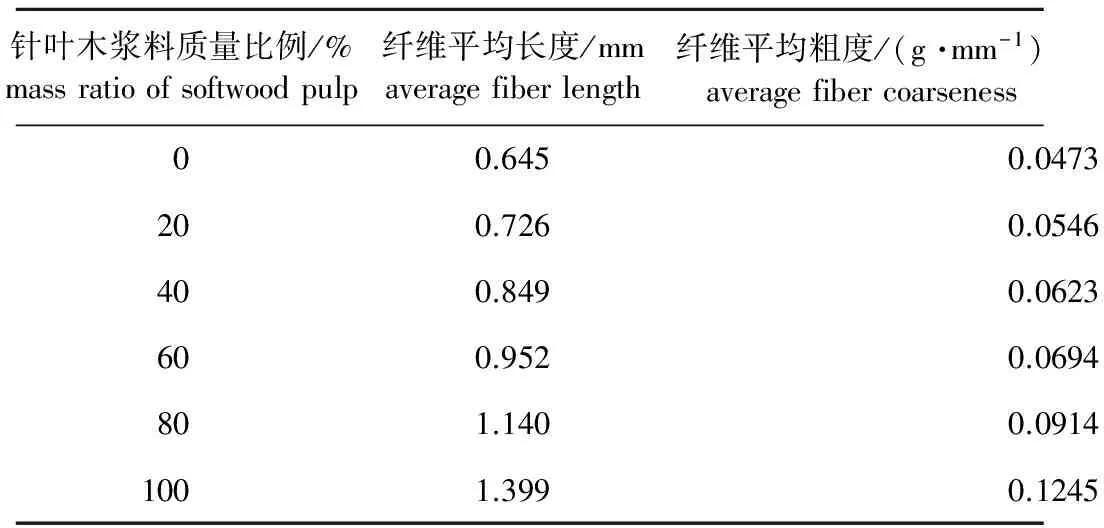
表4 含不同针叶木浆混合浆料的纤维平均尺寸
Kerekes等[11]在总结前人所做工作的基础上,得出式(1)中参数a的范围在1.5~25,参数b的范围在1.7~3.0。Bennington等[12]通过转矩流变仪测量木浆纤维悬浮液的屈服应力,得出a和b的取值范围分别在1.18~24.5和1.25~3.02之间,而本实验中所求得的针叶木和阔叶木的a和b均在此范围之内,由此验证了实验结果的可靠性。
由图2还可以看出,在相同质量分数范围内,针叶木显示出比阔叶木更高的屈服应力。这说明纤维尺寸越大,相邻纤维更容易接触并纠缠在一起,增强了纤维间机械连接及纤维网络的强度,从而使悬浮液在宏观上呈现出更高的屈服应力。比较针叶木和阔叶木可知,纤维尺寸越大系数a增加而指数b则减小。
2.2.2 相同集聚因子范围内的屈服应力 Kerekes等[13]综合考虑了质量分数与纤维结构尺寸,提出了集聚因子(N)以表征纤维交织情况,其表示在悬浮液内以平均纤维长度为直径的球形区域内的纤维数量。对于纸浆纤维悬浮液,集聚因子可以近似由质量分数(Cm)、纤维长度(L)和纤维粗度(δ)来表示,如式(2)所示:
(2)
将式(2)中与纤维尺寸有关的参数统一为形状系数(β),则得到式(3):
N≈5·Cm·β
(3)
本实验中所使用的针叶木浆料形状系数βA=15.72,阔叶木浆料形状系数βB=8.8。图3为两种纸浆纤维悬浮液在相同集聚因子范围内的屈服应力。
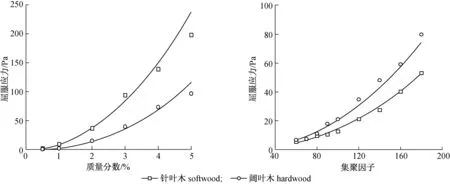
图2 不同质量分数纤维悬浮液屈服应力 图3 不同集聚因子纤维悬浮液屈服应力
Fig.2 Variation of the yield stress versus mass fraction Fig.3 Variation of the yield stress versus crowding number
集聚因子在一定程度上反映了纤维交织情况,集聚因子越大,纤维数量则越多,形成的纤维网络越紧密,因此相应的纸浆悬浮液的屈服应力也越大。然而,在相同集聚因子下,两种浆料的屈服应力并不相同,形状参数较小的阔叶木浆料有更高的屈服应力。
将图2和图3中所有实验数据进行非线性回归得到屈服应力与质量分数和形状系数之间的关系,如式(4)所示(相关系数R2=0.986):
(4)
由式(3)带入式(4),可得:
τy≈0.003·N2.2/β0.6
(5)
由式(5)可以看出,屈服应力并不能由单一集聚因子的函数来表示,其可能的原因是悬浮液中纤维网络结构的强度与纤维接触点处的作用力、接触点的数量密切相关[12]。接触点的数量很难测量与统计,但其同时受到纤维数量和纤维尺寸的影响。Dodson预测单根纤维上接触点与集聚因子成正比,而同时又与纤维长径比成反比[14],这与式(5)中屈服应力与集聚因子和形状系数之间关系相似。阔叶木浆料纤维形状系数较小,在相同集聚因子下同体积悬浮液中纤维间接触点总数较多,因此其屈服应力大于针叶木浆料。
2.3 混合浆料纤维悬浮液的屈服应力
图4所示为不同质量分数下,针叶木浆料与阔叶木浆料按照不同质量比例混合后纤维悬浮液的屈服应力。可以看出混合浆料的屈服应力值均处在相应质量分数下两种浆料独自存在时屈服应力值的区间内,并且随着针叶木浆料在混合浆料中的质量比例(x)的增加而呈现出近似线性递增(如图中线条所示),即:
τy(AB)≈τy(B)+(τy(A)-τy(B))/100·x
(6)
但由表3数据可看出混合浆料的平均长度及粗度与针叶木浆料的质量比例未呈线性相关。将实验数据进行非线性回归如式(7)所示(R2=0.997),混合浆料屈服应力与质量分数及形状系数之间的关系与单一种类浆料(式(4))基本一致。
(7)
因此在相同质量分数下混合浆料的形状系数应满足:
(8)
如图5所示,混合浆料形状系数的1.6次方随着针叶木浆料在混合浆料中的质量分数的增加基本呈线性关系(如图中线条所示)。因而可以推测,对于纤维结构尺寸并不均匀的某种浆料,可以看成是由多种单一形状系数的纤维按照一定的比例混合而成,该种浆料的屈服应力与各组分屈服应力之间也应存在相应的函数关系。
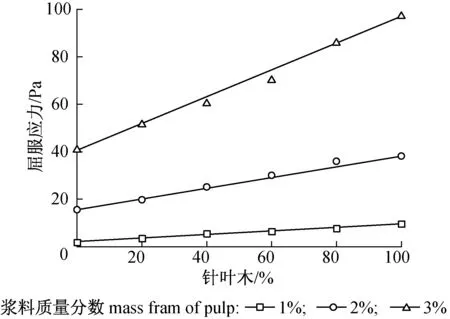
图4 混合浆料纤维悬浮液屈服应力
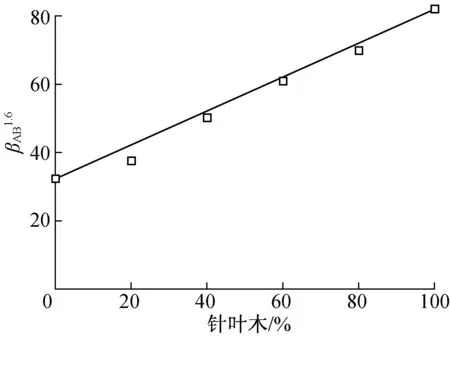
图5 混合浆料形状系数(βAB)的1.6次方
3 结 论
3.1 在相同质量分数范围内,被测针叶木浆由于纤维尺寸较大,纤维网络有较高强度,其屈服应力也大于阔叶木浆,并且纤维尺寸增大,屈服应力与质量分数的幂率关系中乘数项系数增加而指数项系数减小。
3.2 虽然集聚因子全面考虑了纤维悬浮液质量分数和纤维尺寸,在一定程度上反映了纤维交织情况,但屈服应力并不能由单一集聚因子的函数来表示,还与形状系数成反比,即τy≈0.003·N2.2/β0.6。因此,在相同集聚因子范围内,形状参数较小的阔叶木浆料具有更高的屈服应力。
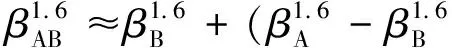
[1]ANDERSSON S R,RASMUSON A. Flow measurements on a turbulent fibre suspension by laser doppler anemometry[J]. AIChE Journal, 2000,46(6):1106-1119.
[2]高扬,倪永,张凤山,等. 制浆造纸工业的可持续发展与构建集成的林产生物质精炼工业[J]. 林产化学与工业,2010,30(2):113-120. GAO Y,NI Y,ZHANG F S,et al. Sustainable development of pulp-and-paper industry combining with integrated forest-biomass biorefinery[J]. Chemistry and Industry of Forest Products,2010,30(2):113-120.
[3]沙九龙,王晨,JAMES O,等. 纸浆纤维悬浮液屈服应力及其在造纸工业中的应用研究进展[J]. 中国造纸学报,2016,31(3):50-57. SHA J L,WANG C,JAMES O, et al. Research progress about the yield stress of pulp fiber suspension and its application in pulp and paper industry [J]. Transactions of China Pulp and Paper,2016,31(3):50-57.
[4]SWITZER L H,KLINGENBERG D J. Rheology of sheared flexible fiber suspensions via fiber-level simulations[J]. Journal of Rheology, 2003,47(3):759-778.
[5]STICKEL J J,KNUTSEN S J, LIBERATORE W M,et al. Rheology measurements of a biomass slurry: An inter-laboratory study[J]. Rheologica Acta,2009,48(9):1005-1015.
[6]KITANO T,KATAOKA T,SHIROTA T. An empirical-equation of the relative viscosity of polymer melts filled with various inorganic fillers[J]. Rheologica Acta,1981,20(2):207-209.
[7]WOLF B,WHITE D,MELROSE R J,et al. On the behaviour of gelled fibre suspensions in steady shear[J]. Rheologica Acta,2007,46(4):531-537.
[8]沙九龙. 纸浆纤维悬浮液的屈服应力与触变特性的研究[D]. 南京: 南京林业大学博士学位论文,2016. SHA J L.The yielding and thixotropic flow behavior in pulp fiber[D].Nanjing:Doctroral Dissertation of Nanjing Forestry University,2016.
[9]KEREKES R J. Rheology of fiber suspensions in papermaking: An overview of recent research[J]. Nordic Pulp and Paper Research Journal, 2006,21(5):598-612.
[10]VAN DER AERSHOT E,MEWIS J. Equilibrium properties of reversibly flocculated dispersions[J]. Colloids and Surfaces,1992,69(1):15-22.
[11]KEREKES R J,SOSZYNSKI R M,TAM DOO P A. The flocculation of pulp fibres[C]∥PUNTON V. Proc. 8th Fundamental Research Symposium, London: Oxford,1985:265-310.
[12]BENNINGTON C P J,KEREKES R J, GRACE R J. The yield stress of fibre suspensions[J]. The Canadian Journal of Chemical Engineering,1990,68(5):748-757.
[13]KEREKES R J, SCHELL C J.Characterization of fiber flocculation by a crowding factor[J]. Journal of Pulp and Paper Science,1992,18(1):32-38.
[14]DODSON C T J. Fiber crowding, fiber contacts and fiber flocculation[C]∥University of Washington. The Pacific Section Tappi 48th Annual Seminar. Seattle:[s.n.], 1995.
Influence of Fiber Size on Yield Stress of Bleached Kraft Wood Pulp Fiber Suspension
WANG Chen, ZHENG Xuemei, ZHANG Hui, SHA Jiulong, CHENG Jinlan
(1.Jiangsu Provincial Key Lab of Pulp and Paper Science and Technology, Nanjing Forestry University, Nanjing 210037,China; 2.Jiangsu Co-Innovation Center for Efficient Processing and Utilization of Forest Resources,Nanjing Forestry University, Nanjing 210037, China)
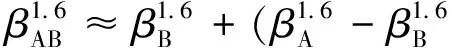
bleached kraft wood pulp; fiber suspension; yield stress; crowding number
10.3969/j.issn.0253-2417.2017.03.012
2016-05-13
江苏省高校优势学科建设工程(无编号);江苏省制浆造纸科学与技术重点实验室开放基金资助(201317)
王 晨(1981— ),男,江苏南京人,讲师,博士,主要从事制浆造纸装备研究;E-mail: chenwang8102@163.com
*通讯作者:张 辉(1962— ),男,江苏启东人,教授,博士,主要从事制浆造纸装备研究;E-mail: zhnjfu@163.com。
TQ35;TS71
A
0253-2417(2017)03- 0089-06
王晨,郑学梅,张辉,等.纤维尺寸对漂白硫酸盐木浆悬浮液屈服应力的影响[J].林产化学与工业,2017,37(3):89-94.
