基于连续直觉模糊相似测度的多属性群决策方法
2017-07-05陶志富曹博学
罗 敏,周 晗,陶志富,吴 澎,曹博学
(1.安徽大学 经济学院,安徽 合肥 230601; 2.安徽大学 数学科学学院,安徽 合肥 230601)
基于连续直觉模糊相似测度的多属性群决策方法
罗 敏1,周 晗2,陶志富1,吴 澎2,曹博学2
(1.安徽大学 经济学院,安徽 合肥 230601; 2.安徽大学 数学科学学院,安徽 合肥 230601)
针对区间直觉模糊数在信息集成时存在处理上的复杂性问题,利用连续区间直觉模糊有序加权平均(C-IVIFOWA)算子,将区间直觉模糊信息转化为含参数的直觉模糊信息,定义了一种连续区间直觉模糊相似测度,研究了其优良性质,并基于该连续区间直觉模糊相似测度构建两个优化模型确定群决策中的专家权重和属性权重,同时提出了基于新的连续区间直觉模糊相似测度的模糊多属性群决策方法,最后通过ERP软件评估群决策分析了该方法的可行性与有效性。
群决策;C-IVIFOWA算子;相似测度;区间直觉模糊数
多属性群决策中,由于客观世界的复杂性和人类评价的模糊性,属性值可由模糊数表达。ZADEH[1]用隶属度函数描述集合中元素属于某种属性的模糊程度,并提出模糊集理论。 ATANASSOV等[2-3]在此基础上定义了非隶属函数和犹豫函数,建立了直觉模糊集理论并进一步地将隶属度、非隶属度和犹豫度扩展为区间数,创建区间直觉模糊集理论。属性值用区间直觉模糊数表达的多属性群决策,即为区间直觉模糊多属性群决策。近年来,学者们对区间直觉模糊多属性群决策展开深入研究并广泛应用于医学诊断、经济预测、管理决策等领域[4-9]。
目前,区间直觉模糊多属性群决策研究主要集中在以下两个方面:①区间直觉模糊数集成算子的确定[10-12];②属性权重和专家权重的确定[13-17]。文献[10]提出了区间直觉模糊数算术平均算子、区间直觉模糊数加权算术平均算子、区间直觉模糊数几何平均算子和区间直觉模糊数加权几何平均算子,并应用于实例中。在此基础上,文献[11]定义了区间直觉模糊数有序加权平均算子和区间直觉模糊数混合集结算子。由于区间直觉模糊数集成时较为复杂,文献[12]基于连续区间加权平均(C-OWA)算子,定义连续区间直觉模糊有序加权平均(C-IVIFOWA)算子,该算子通过引入态度参数将隶属度和非隶属度由区间形式转化为实数形式,降低了模型求解的难度。
为了确定属性权重,文献[13]依据TOPSIS方法和区间直觉模糊集的精确函数,构建求解属性权重的线性规划模型。文献[14]基于灰色关联的分析方法,构建正负理想方案与正理想方案灰色关联度偏差最小化的多目标规划模型。文献[15]定义不同方案的偏差函数,并以所有属性对各决策方案总偏差最大化为目标建立优化模型。文献[16]从区间直觉模糊数的几何意义出发,构建熵最大化的属性权重求解模型、专家个体与综合专家的灰色关联度和熵最大化的决策者权重求解模型。文献[17]通过建立基于交叉熵原理的优化模型确定专家权重和属性权重。
但大多数研究中,属性权重或专家权重均为已知条件,两者均未知的研究较少。笔者在专家权重和属性权重完全未知情况下,首先基于C-IVIFOWA算子和向量夹角余弦,提出一种新的连续区间直觉模糊相似测度。其次,建立非线性规划模型求解最优专家权重和属性权重,并计算不同方案的综合属性值,利用相似性函数和精确函数对方案进行排序。最后,笔者将该方法应用于ERP软件的评估中。
1 基本定义
为了克服传统模糊集仅用隶属度定义模糊集的不足,文献[3]提出了直觉模糊集。
定义1 在给定的论域X={x1,x2,…,xn}下,将直觉模糊集A定义为:
A={〈xi,μA(xi),vA(xi)〉|xi∈X}
(1)
其中,μA(xi)、vA(xi)分别为xi属于A的隶属度和非隶属度,对任意xi∈X,有μA(xi)∈[0,1],vA(xi)∈[0,1],且μA(xi)+vA(xi)≤1,并称πA(xi)=1-μA(xi)-vA(xi)为xi属于A的犹豫度。
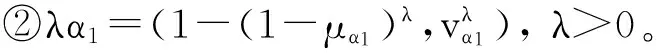
为了对直觉模糊数进行排序,文献[18]定义了直觉模糊数αi的相似性函数和精确函数:

(2)
h(αi)=μαi+vαi
(3)
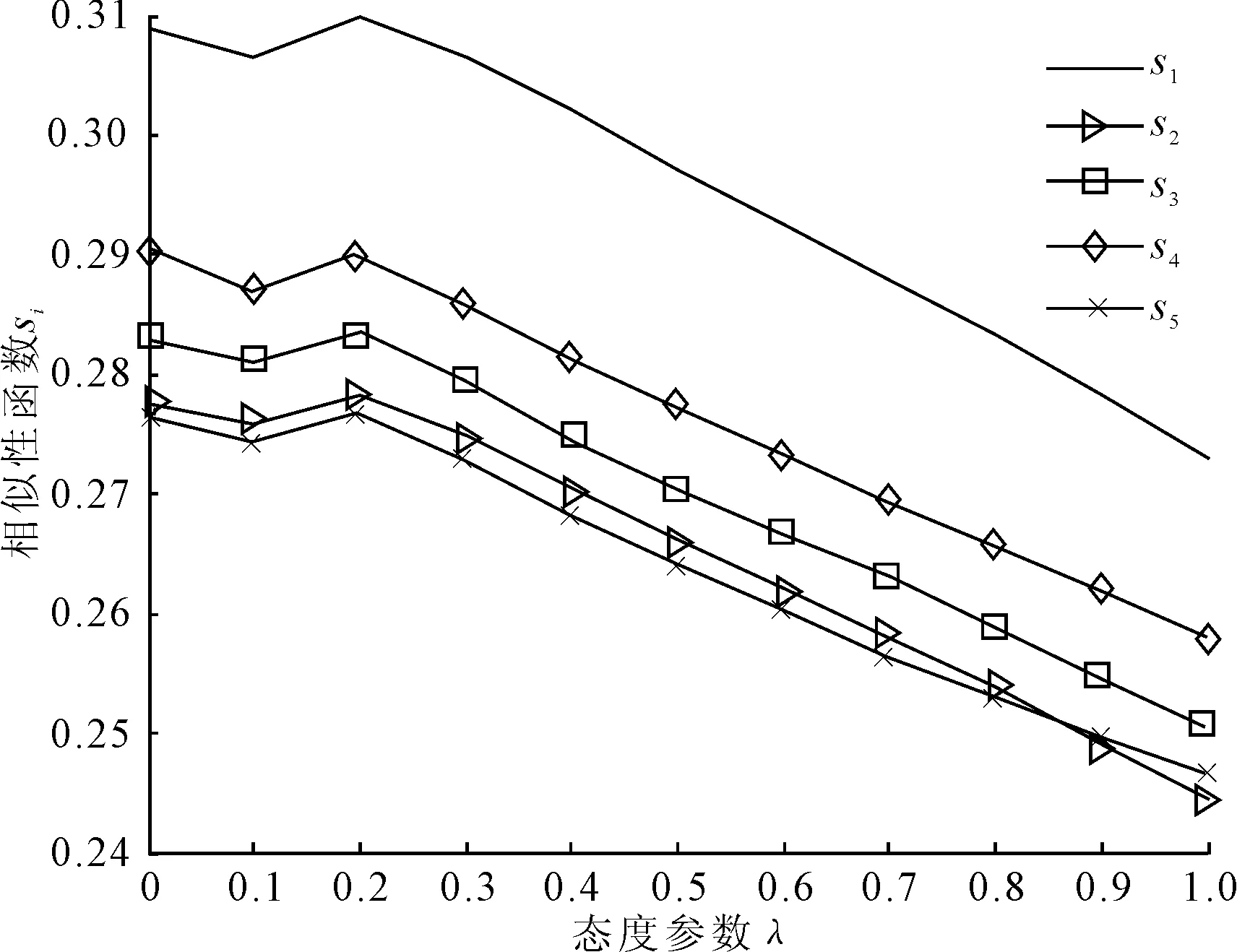
且对任意两个直觉模糊数α1=(μα1,vα1)和α2=(μα2,vα2),排序规则如下:①当s(α1)=s(α2)时,若h(α1)=h(α2),则α1=α2;若h(α1)>h(α2),则α1>α2;若h(α1) 考虑到实际问题的不确定性和复杂性,隶属度和非隶属度应由区间数表示,而非单一的实数值,因此ATANASSOV等提出了区间直觉模糊集。 (4) 为了集结区间直觉模糊数,文献[12]提出了一种连续区间直觉模糊有序加权平均(C-IVIFOWA)算子。 (5) 由定义3可以看出,C-IVIFOWA算子通过态度参数λ将区间直觉模糊数转化成含参数的直觉模糊数,这样可以减小区间直觉模糊数计算的复杂度,提高区间直觉模糊决策的计算效率。为了方便表示,笔者用gλ来表示。 区间数的运算并不遵从常规加减法运算的一般规律,在信息集成时较为复杂。为了准确衡量集成结果的好坏,笔者基于C-IVIFOWA算子和向量夹角余弦,定义了一种新的连续区间直觉模糊相似测度。 2.1 连续区间直觉模糊相似测度 (6) 证明 ①~③显然成立,下面证明④。 2.2 基于连续区间直觉模糊相似测度的专家权重确定模型 其中,效益型指标: (7) 成本型指标: (8) 2.3 基于连续区间直觉模糊相似测度的属性权重确定模型 (9) 2.4 基于连续区间直觉模糊相似测度的模糊群决策方法 则基于连续区间直觉模糊相似测度的群决策方法计算步骤如下: (10) (11) 图1 最优专家权重 同时,为了分析态度参数对模型(M2)最优属性权重的影响,取λ∈[0,1],求解模型(M2)得到最优专家权重,如图2所示。由图2可以看出,随着态度参数λ的增大,各个最优属性权重均有一定的波动,但是软件服务水平属性仍然是最重要的属性,当λ≤0.141 5或λ≥0.481 2时,功能完善程度属性为重要性最差的属性;当0.141 5<λ≤0.158 3时,系统潜在风险属性为重要性最差的属性;当0.158 3<λ<0.481 2时,操作系统平稳性属性为重要性最差的属性。 图2 最优属性权重 为了分析态度参数λ对决策结果的影响,取λ∈[0,1],并计算相似性函数值,结果如图3所示。由图3可以看出,随着态度参数λ的增大,各个方案的相似性函数值均呈现先小幅递减,然后小幅递增,再单调递减的状况,但是方案o1的相似性函数值始终是最大的,故该方案始终是最优方案,而方案o2和o5则差异不大。 图3 相似性函数 笔者针对专家权重和属性权重未知的区间直觉模糊多属性群决策问题,在C-IVIFOWA算子的基础上,通过引入态度参数,将区间直觉模糊决策矩阵转化为含参数的直觉模糊决策矩阵;并基于向量夹角余弦,定义了一种新的连续区间直觉模糊相似测度,构建优化模型求解最优的专家权重和属性权重;同时提出了一种基于连续区间直觉模糊相似测度的模糊多属性群决策方法;最后通过ERP软件评估群决策论证了该方法的可行性和有效性。 与其他区间直觉模糊相似测度相比较,连续区间直觉模糊相似测度基于C-IVIFOWA算子,将难于处理的区间直觉模糊信息转化为易于处理的直觉模糊信息,并用数值准确衡量了区间直觉模糊数集成效果的好坏。特别地,与Jaccard相似度相比,笔者采用的相似测度可用来解决区间直觉模糊问题,而Jaccard相似度用来衡量实体的字符串相似程度[20],并被广泛应用于实体识别领域。此外,连续区间直觉模糊相似测度可以用来构建优化模型确定属性权重和专家权重,决策者还可以依据自己的风险态度选择适合自己的最优方案。 笔者仅研究了属性不相互关联的区间直觉模糊多属性群决策问题,下一步需考虑将笔者方法与Choquet积分进行结合,以便更好地处理具有属性关联的群决策问题。与此同时,为了确保专家权重的客观性,还应考虑不同专家在决策时共识性的达成问题。 [1]ZADEHLA,Fuzzysets[J].InformationandControl, 1965,8(3):338-353. [2]ATANASSOVK,GARGOVG.Interval-valuedintuitionisticfuzzysets[J].FuzzySetsandSystems, 1989,31(3):343-349. [3]ATANASSOVK.Intuitionisticfuzzysets[J].Physica-VerlagHD, 1999,20(1):87-96. [4]NGUYENH.Anewinterval-valuedknowledgemeasureforinterval-valuedintuitionisticfuzzysetsandapplicationindecisionmaking[J].ExpertSystemswithApplications, 2016,56(C):143-155. [5] 徐泽水.直觉模糊信息集成理论及应用[M].北京:科学出版社,2008:44-68. [6] 李娅,邓鑫洋,邓勇.一种新的区间直觉模糊集决策方法:区间证据组合的角度[J].控制与决策,2014,29(6):1143-1147. [7] 王坚强.信息不完全确定的多准则区间直觉模糊决策方法[J].控制与决策,2006,21(11):1253-1256. [8] 樊雷,雷英杰,段索力.区间直觉模糊统计判决与决策[J].系统工程理论与实践,2011,31(9):1790-1797. [9] 高明美,孙涛,朱建军.基于改进熵和新得分函数的区间直觉模糊多属性决策[J].控制与决策,2016,31(10):1757-1764. [10] 徐泽水.区间直觉模糊信息的集成方法及其在决策中的应用[J].控制与决策,2007,22(2):215-219. [11] 徐泽水,陈剑.一种基于区间直觉判断矩阵的群决策方法[J].系统工程理论与实践,2007,27(4):126-133. [12]ZHOUL,TAOZ,CHENH,etal.Continuousinterval-valuedintuitionisticfuzzyaggregationoperatorsandtheirapplicationstogroupdecisionmaking[J].AppliedMathematicalModelling, 2014,38(7-8):2190-2205. [13] 张英俊,马培军,苏小红,等.属性权重不确定条件下的区间直觉模糊多属性决策[J].自动化学报,2012,38(2):220-228. [14] 刘勇,FORRESTJ, 刘思峰,等.基于区间直觉模糊的动态多属性灰色关联决策方法[J].控制与决策,2013,28(9):1303-1308. [15] 卫贵武.权重信息不完全的区间直觉模糊数多属性决策方法[J].管理学报,2008,5(2):208-211. [16] 李艳玲,殷新丽,杨剑.区间直觉模糊决策中专家与属性权重确定方法[J].计算机工程与应用,2016,52(18):158-161. [17] 李宝萍,陈华友.一类基于交叉熵的区间直觉模糊多属性群决策的新方法[J].统计与决策,2014(1):20-23. [18]ZHANGX,XUZ.Anewmethodforrankingintuitionisticfuzzyvaluesanditsapplicationinmulti-attributedecisionmaking[J].FuzzyOptimizationandDecisionMaking, 2012,11(2):135-146. [19] 戚筱雯,梁昌勇,张恩桥,等.基于熵最大化的区间直觉模糊多属性群决策方法[J].系统工程理论与实践,2011,31(10):1940-1948. [20] 潘磊,雷钰丽,王崇骏,等.基于权重的Jaccard相似度度量的实体识别方法[J].北京交通大学学报,2009,33(6):141-145. TAO Zhifu:Lect.; School of Economics, Anhui University, Hefei 230601, China. AnApproachtoMultipleAttributeGroupDecisionMakingBasedonContinuousIntuitionisticFuzzySimilarityMeasure LUOMin,ZHOUHan,TAOZhifu,WUPeng,CAOBoxue In order to deal with complexity of information aggregation of interval-valued intuitionistic fuzzy numbers, the interval-valued intuitionistic fuzzy information is transformed into the intuitionistic fuzzy information with parameter based on the continuous interval-valued intuitionistic fuzzy ordered weighted averaging (C-IVIFOWA) operator. Then a continuous interval-valued intuitionistic fuzzy similarity measure is defined, and some desirable properties are investigated. Moreover, two optimization-based models are put forward to determine the weights of experts and attributes on the basis of the continuous interval-valued intuitionistic fuzzy similarity measure. Furthermore, a fuzzy multiple attributes group decision making is proposed by using the continuous interval-valued intuitionistic fuzzy similarity measure, finally, a group decision making problem for evaluation on ERP software is used to analyze the feasibility and validity of the proposed method. group decision making; C-IVIFOWA operator; similarity measure; interval-valued intuitionistic fuzzy number 2095-3852(2017)03-0299-07 A 2016-11-12. 陶志富(1985-),男,安徽庐江人,安徽大学经济学院讲师,博士,主要研究方向为运筹与管理、预测和决策分析. 国家自然科学基金项目(71371011);安徽大学卓越应用经济人才基金项目(J10118412003);安徽大学科研训练计划基金项目(KYXL2016006);安徽大学创新创业实验基金项目(201610357473,201610357119,201610357347). C934 10.3963/j.issn.2095-3852.2017.03.012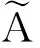
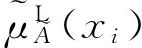
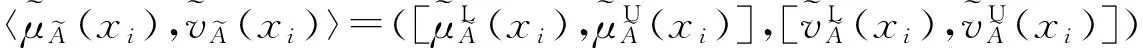


2 基于连续区间直觉模糊相似测度的多属性群决策方法
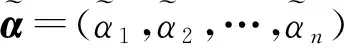
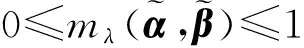
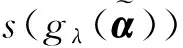

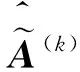
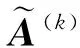


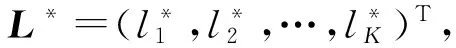

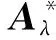
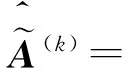
3 案例分析
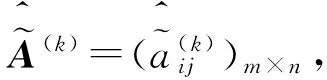
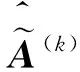
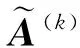

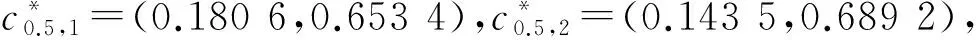
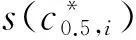

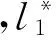

4 结论
