基于动态预测的有源电力滤波器选择性谐波补偿方法
2017-07-03李锦彬陈冲
李锦彬, 陈冲
(1.福州大学 电气工程与自动化学院, 福建 福州 350116; 2.福建工程学院 信息科学与工程学院, 福建 福州 350118)
基于动态预测的有源电力滤波器选择性谐波补偿方法
李锦彬1,2, 陈冲1
(1.福州大学 电气工程与自动化学院, 福建 福州 350116; 2.福建工程学院 信息科学与工程学院, 福建 福州 350118)
提出一种基于参考电流动态预测的选择性补偿方法。通过滑窗迭代DFT法提取与参考电流相关的特定次谐波;把动态预测算法植入补偿电流控制环节,预测下一拍的指令电流信号,并引入误差修正器提高预测精度,在此基础上计算逆变器的参考电压矢量;利用空间矢量脉宽调制法获得PWM信号,驱动三相变流器从而输出三相电压,实现选择性补偿。仿真和实验证明了该方法的正确性和可行性。
有源电力滤波器; 选择性谐波补偿; 动态预测; 无差拍控制
电力电子装置在给用户带来用电方便的同时也向公用电网注入大量的谐波、无功及不平衡电流,给电网造成污染,从而影响其他用户用电,甚至使某些敏感设备无法正常运行[1-2]。有源电力滤波器(active power filter, APF)是滤除谐波和补偿无功的新型电力电子装置[3],近年来受到国内外学者的关注、研究。然而,数字系统固有的计算延时放大了控制延时的负面效应,若不进行滞后补偿将降低APF的补偿性能,甚至使系统不稳定。谐波阶次越高,系统延时带来的负面影响越大,还可能出现谐波放大的现象[4]。针对消除补偿系统延时问题,可以引进新型的控制算法对给定信号进行预测,相当于增加一个相位超前环节以对消滞后环节,改善APF系统的性能。采用基于谐波指令电流动态预测法的前馈控制策略不增加额外的硬件成本,能有效地降低系统延时带来的影响。
实际应用中的APF通常按选择性补偿策略来设计,主要有3个方面原因:(1)APF的带宽有限,补偿20 次以上的谐波电流时效果不理想,而且这些阶次的谐波在总谐波中的占有率很小,不予补偿并不会影响电网供电。(2)为了更加合理地分配APF的容量,实际应用中经常需要对补偿成分进行限幅;由于选择性补偿策略先是对单次谐波进行检测,而且无功和负序电流都是基频,所有的补偿成分都可以进行有效的限幅。(3)在有源与无源混合使用的场合,APF对谐波和无功的补偿必须避开无源补偿的成分;此外,选择性补偿策略可以避开个别配电网存在的谐振频点。
目前,针对APF选择性谐波补偿的研究主要包括选择性谐波检测算法[5]和对指定次谐波电流综合控制策略[6]。
新型的选择性谐波补偿策略采用动态预测算法预测下一采样周期的参考信号,并引入误差修正机制来提高预测精度。通过无差拍控制技术得出三相逆变器所需的电压空间矢量,经空间矢量脉宽调制获得PWM信号,实现实时补偿。
搭建SIMULINK仿真模型进行仿真研究,并在APF实验样机验证基于动态预测算法的选择性补偿策略,仿真和实验结果都证明了该预测算法的正确性和有效性。
1 APF选择性补偿原理
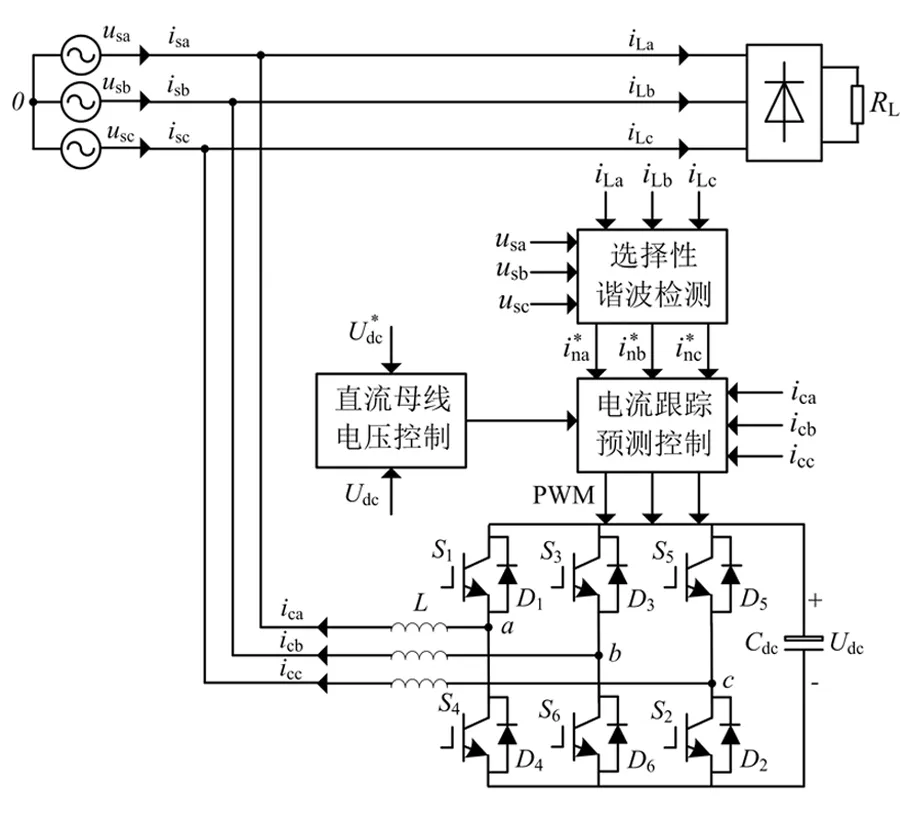
图1 三相三线并联型APF原理示意图 Fig.1 Schematic of three-phase three-wire shunt APF
系统的工作流程为:(1)利用选择性谐波检测方法提取负载电流中的待补偿谐波分量;(2)按预测算法对所检测的谐波电流进行下一拍预测,反极性后即为补偿控制系统的参考值;(3)通过电流跟踪控制,产生PWM信号,驱动开关管,从而使逆变器输出电压,与电网电压一起作用在电感上,输出谐波电流,注入电网对消掉待补偿的谐波成分。
2 选择性谐波检测方法
对指定次谐波的快速、准确检测是APF实现选择性补偿的前提,目前的检测方法主要是采用多同步旋转坐标变换的检测方法[5],或者采用引入旋转参考相量[7]的方法,这些方法都要采用低通滤波器滤出交流分量。随着检测的谐波次数增加,同步旋转坐标系也成倍递增,因此系统比较复杂。笔者采用滑窗迭代离散傅里叶变换(discreet Fouriet transform,DFT)法提取特定次谐波,检测精度高且动态响应快。图2给出了特定次谐波检测的原理。
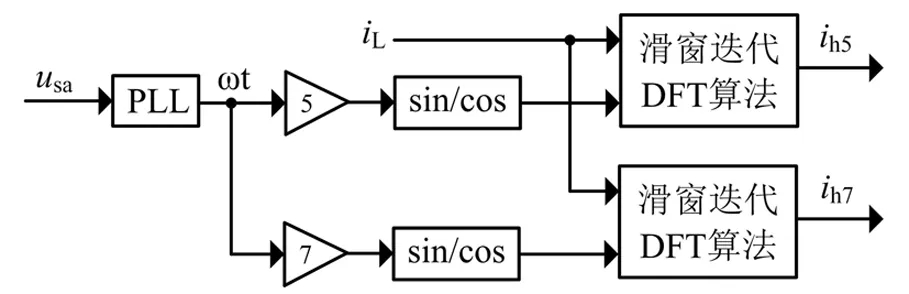
(a)指定次谐波检测
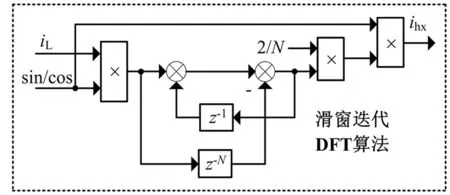
(b)滑窗迭代DFT算法流程图2 选择性谐波检测算法Fig.2 Selective harmonic detection algorithm
3 电流跟踪动态预测控制
3.1 电流无差拍控制策略
根据图1可列出APF回路电压方程:
(1)
式中,uao、ubo、uco为变流器输出电压。对式(1)离散化,得到如下的无差拍模型:
(2)
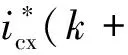
APF是数字控制系统,对谐波电流的提取、参考电压的计算等都需要指令周期的积累。因此,APF当前拍发出的PWM脉冲实际上要等下一拍才会起作用,产生了固有一拍的控制延时。消除固有一拍控制延时的方法是在谐波检测环节加入超前校正,预测下一拍的参考电流是消除控制延时的有效方法。因此式(2)所示的无差拍模型适合实现预测控制。
3.2 动态预测算法
若正弦信号表示为
(3)
对x(t)进行等间隔采样,采样间隔为Ts,则得到序列(k为序列的序号)
(4)
当采样频率足够高时,有
(5)
将x′(n-1)在n时刻一阶泰勒展开可得到
(6)
进而
(7)
而n-1时刻的导数可近似表示为
(8)
考虑到在任意时刻
(9)
所以有
(10)
将式(8)、(10)代入式(7)可得
(11)
再将式(11)代入式(5)可得
(12)
根据式(12),用当前拍及前一拍的采样值x(n)和x(n-1)可估计下一拍的采样值x(n+1)。由泰勒展开原理可知:若连续函数无限次可导,只要历史采样值足够多,就能精确地拟合出有限时间内的函数。因为正弦函数具有如式(9)所示的微分性质,导数的阶越高,对应的差分方程阶次也越高,参与估计未来值得历史样本数据也就越多,估计值也就越接近真实值。
APF是采用选择性补偿策略,电流参考采用指定次谐波提取方法,已经滤除了单次谐波的高频分量,因此差分运算易使噪声放大的问题在此不存在。
理论上,式(12)所示的差分方程可以计算更高阶,但考虑到对电力谐波的滤出不需要达到绝对的零稳态误差,所以本算法只使用到二次导数。
3.3 补偿电流预测控制
根据式(12)所示的单频信号预测式,对n次谐波补偿电流参考值的一拍预测可表示为:
(13)
上述预测方法没有引入误差修正机制,属于开环控制。因此必须加入校正量来消除误差,预测电流误差修正流程如图3所示。
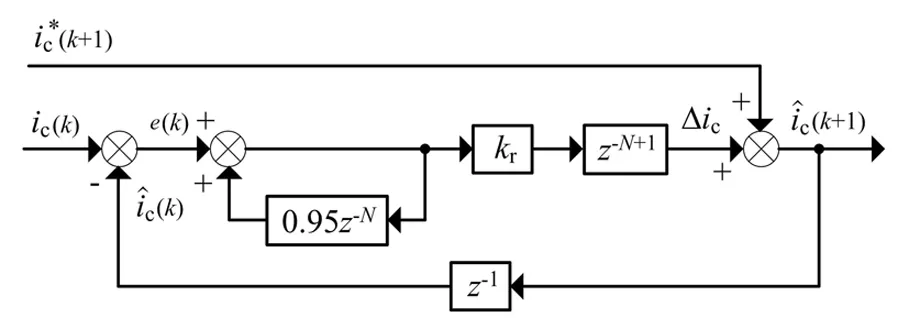
图3 预测电流误差修正流程图Fig.3 Flowchart of current forecast error correction
(14)
4 仿真分析
4.1 仿真参数
为了验证动态预测算法的正确性,搭建了三相并联型APF的SIMULINK模型。APF主要参数为:电网电压为380 V,频率为50 Hz;非线性负载采用三相不可控整流器带纯电阻负载,阻值10 Ω;直流侧电容10 000 μF,直流母线电压参考值750 V;APF输出端滤波电感1.5 mH;采样频率12.8 kHz;电流预测误差补偿系统的稳定系数kr为0.98。
负载电流(以A相为例)波形及其频谱如图4所示。负载谐波电流以低次为主,主要谐波成分是5、7、11、13、17和19次,总畸变率THD=26.65%。
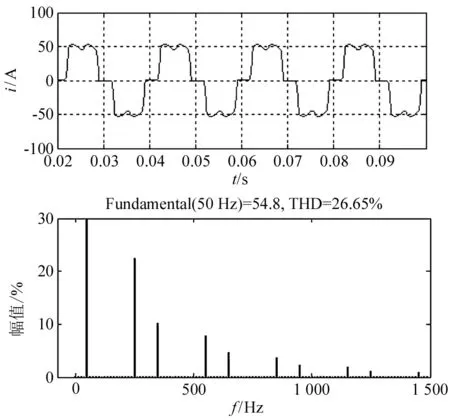
图4 非线性负载电流及频谱(以A相为例)Fig.4 Nonlinear load current and corresponding spec- trum(in the case of phase A)
4.2 补偿5次谐波
由图4可知:负载电流中5次谐波的占有率最高。图5是仅补偿5次谐波的仿真结果。采用动态预测控制策略后,总谐波畸变率降为15.01%;其中补偿前负载电流中的5次谐波占有率约22%,经补偿后5次谐波占有率几乎为0,补偿效果比较明显。
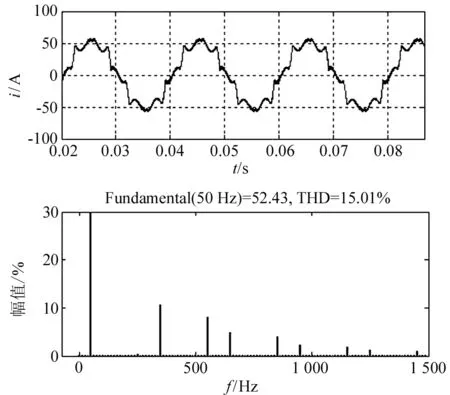
图5 选择补偿5次谐波的仿真结果 Fig.5 Simulation results post 5 times of harmonic compensation
4.3 补偿5、7次谐波
图6是补偿负载电流中的5、7次谐波的仿真结果。补偿之后总畸变率降为10.74%,5、7次谐波也基本滤除。
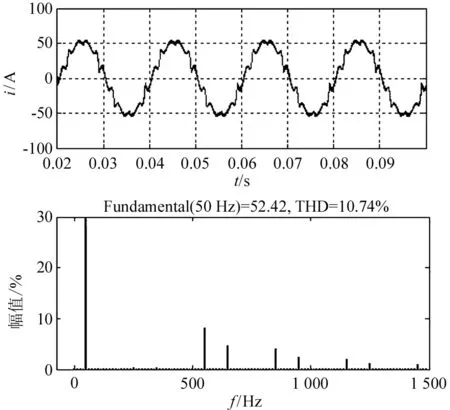
图6 选择补偿5、7次谐波的仿真结果Fig.6 Simulation results post 5 and 7 times of harmonic compensation
4.4 补偿5、7、11、13、17和19次谐波
图7是补偿负载电流中5、7、11、13、17和19次谐波的仿真结果。补偿之后总畸变率降为3.46%,小于5%,进一步验证了按指定次谐波补偿方式对谐波电流进行抑制是合理的。
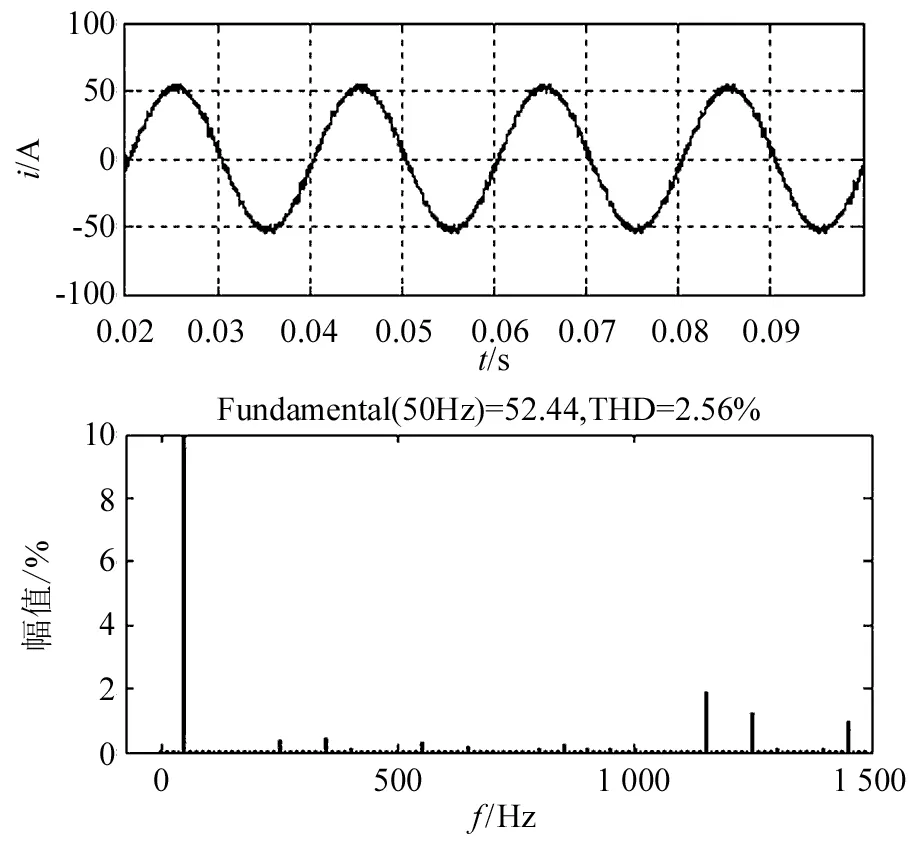
图7 选择补偿5、7、11、13、17、19次谐波的仿真结果Fig.7 Simulation results post 5, 7, 11, 13, 17 and 19 times of harmonic compensation
4.5 动态特性分析
为了验证APF补偿系统的动态性能,在t=0.1 s时,负载电阻由原来的10 Ω突降为5 Ω。按4.4节的补偿成分进行补偿,仿真结果如图8所示。由图8可知,负载突变后,大约经过15 ms过渡到新的平衡状态,说明该预测控制策略具有较快的动态响应速度。
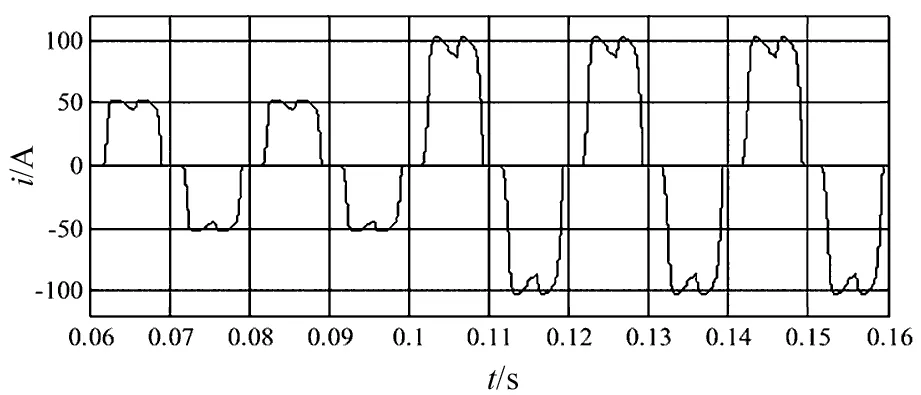
(a)负载电流
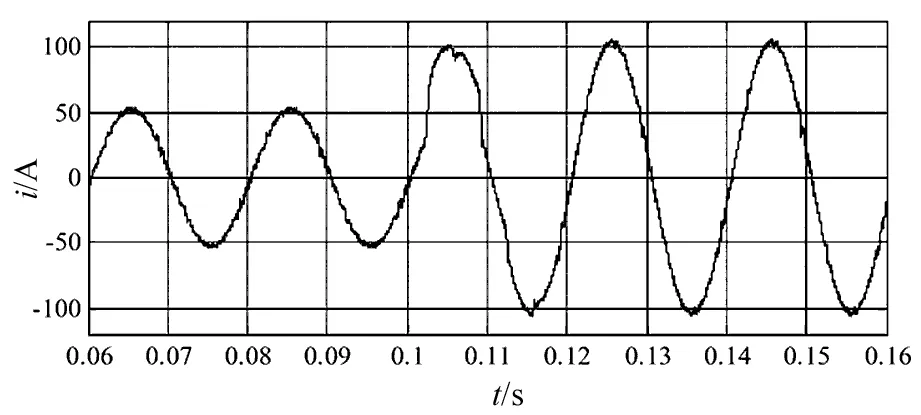
(b)补偿后网侧电流图8 负载突变时的动态特性Fig.8 Dynamic characteristics under load fluctuation
5 实验验证
为验证该方法的有效性,在实验室的APF样机验证选择性补偿的稳态性能和动态响应性能。样机参数与仿真模型参数一致,实验结果如图9所示。其中:第一通道为A相负载电流波形,存在负载突变情况;第二通道为补偿5、7、11、13、17和19次谐波后电网侧的电流波形。由网侧电流波形可知:负载固定时,补偿后电流的正弦度很高;负载突变时动态响应速度快,调节时间大约15 ms,满足工程要求。

图9 选择补偿5、7、11、13、17、19次谐波的实验结果Fig.9 Experiment results post 5, 7, 11, 13, 17 and 19 times of harmonic compensation
6 结论
(1)动态预测算法可应用于指定次谐波预测,有效地克服了离散系统固有的控制延时。
(2)预测算法是开环的,引入递推重复预测的误差修正机制能提高动态预测的精度,提高鲁棒性。
[1] 王兆安,杨君,刘进军,等.谐波抑制和无功功率补偿[M].北京:机械工业出版社,2005.
[2] 杨君,叶杰,吴钫,等.谐波电流分次补偿控制的等效性研究[J].电力电子技术,2015,49(5):80-83.
[3] 张国荣,邵竹星,陈林.基于改进重复预测原理的并联型有源电力滤波器无差拍控制策略[J].农业工程学报,2012,28(13):172-178.
[4] 谢川,贺超,闫辉,等.基于频率自适应广义积分控制器选择性谐波电流控制策略[J].电工技术学报,2013,28(9):65-72.
[5] 张树全,戴珂,谢斌,等.多同步旋转坐标系下指定次谐波电流控制[J].中国电机工程学报,2010,30(3):55-61.
[6] 刘威葳,丁洪发,段献忠.有源电力滤波器选择性谐波电流控制策略[J].中国电机工程学报,2011,31(27):14-20.
[7] 韩学军,刘万勋,刘广平, 等.基于三相旋转参考相量的并联有源电力滤波器谐波电流精确检测方法[J].电网技术,2008, 32(3):75-83.
(特约编辑:黄家瑜)
Dynamic forecast-based selective harmonic compensation method for active power filter
Li Jinbin1,2, Chen Chong1
(1. College of Electrical Engineering and Automation, Fuzhou University, Fuzhou 350116, China; 2. College of Information Science and Engineering, Fujian University of Technology, Fuzhou 350118, China)
To improve the compensation performance and efficiency of active power filters, a selective harmonic compensation method was proposed based on the dynamic forecast of reference current. Firstly, the specific harmonics associated with the reference current signal was extracted via sliding window iterative DFT method; then the dynamic forecast algorithm was implanted into the compensation current control link to estimate the reference current signal value at the following sampling period, and an error corrector was introduced to improve the prediction accuracy; and then the reference voltage vector of the inverter was calculated; Finally, the PWM signals to control the output voltage of the three-phase converter were obtained by the space vector pulse width modulation method, realizing the selective harmonic compensation. The simulation and experimental results confirm the correctness and feasibility of the proposed method.
active power filter; selective harmonic compensation; dynamic forecast; deadbeat control
10.3969/j.issn.1672-4348.2017.03.016
2017-03-09
福建省教育厅资助项目(JA12229)
李锦彬(1973-),男,福建东山人,副教授,硕士,研究方向:电网谐波补偿技术。
TM993
A
1672-4348(2017)03-0279-06
