一类不确定分数阶混沌系统同步的自适应滑模控制方法*
2017-07-03李特袁建宝吴莹
李特 袁建宝 吴莹
(西安交通大学航天航空学院,机械结构强度与振动国家重点实验室, 西安 710049)
一类不确定分数阶混沌系统同步的自适应滑模控制方法*
李特 袁建宝 吴莹†
(西安交通大学航天航空学院,机械结构强度与振动国家重点实验室, 西安 710049)
针对一类系统不确定及受外界干扰的分数阶混沌系统,本文首先将分数阶微积分应用到滑模控制中,构造了一个具有分数阶积分项的滑模面.针对系统不确定及外界干扰项,基于分数阶Lyapunov稳定性理论与自适应控制方法,设计了一种滑模控制器以及分数阶次的参数自适应律,实现了两不确定分数阶混沌系统的同步控制,并辨识出相应误差系统中不确定项及外界干扰项的边界.在分数阶系统稳定性分析中使用的分数阶Lyapunov稳定性理论及相关函数都可以很好地运用到其它分数阶系统同步控制方法中.最后数值仿真验证了所提控制方法的可行性与有效性.
系统不确定, 滑模控制, 分数阶自适应律, 分数阶Lyapunov稳定性理论
引言
尽管分数阶微积分已经有超过三百年的历史了,但将其应用到物理学和工程学的研究直到最近几十年才逐渐引起关注.相对于传统的整数阶微积分,分数阶微积分为描述各种物质和动态过程的记忆及遗传效应提供了有力的数学工具[1].随着分数阶微积分的不断发展,越来越多的研究发现利用分数阶导数能更准确地描述现实中的一些物理现象和动力学系统,因此分数阶导数被广泛应用到众多学科研究及工程领域[2-6].由于分数阶系统更容易稳定的特性,近年来分数阶微积分已经被广泛地应用到系统控制中.尤其在鲁棒性控制方面,分数阶控制表现出更好的控制效果,文献[7]也证实分数阶控制器相较于传统控制器,具有更好的抗干扰性及对外界变化的不敏感性.
混沌作为非线性动力学系统的一种特有运动形式,在物理、化学、生物和信息科学等领域得到了广泛的研究,许多研究已经证实将分数阶微积分引入到一些传统混沌系统中也能表现出混沌特性,比如分数阶Lorenz系统[8],分数阶Duffing系统[9],分数阶Chua电路[10],分数阶Van der Pol振荡器[11]及分数阶Chen系统[12]等等.分数阶混沌系统作为整数阶混沌系统的推广,其动力学特性不仅秉承了混沌系统几乎所有的特点,还具有历史记忆效应、动力学特性与系统阶次密切相关等特点,因此分数阶混沌系统具有比整数阶混沌系统更加复杂的动力学行为.
近年来,分数阶混沌系统的同步控制在保密通信、信号处理和系统控制及其它领域得到了广泛关注和研究,具有比整数阶混沌系统更突出的应用前景和发展前途.目前已经有一些同步控制方法,比如非线性反馈控制[13-14]、主动控制[15]、分数阶控制器[16]、最优化控制[17]、自适应控制[18-19]及滑模控制[20-22]等都被成功应用到分数阶混沌系统的同步问题中.但需要指出,上述控制方法中大多都忽略了系统不确定性及外界环境的干扰,而这些因素在实际工程系统中是不可避免的.但自适应控制可以克服系统参数未知或不确定性,滑膜控制则具有良好的鲁棒性和抗干扰能力,因此这两种控制方法在分数阶非线性系统中的应用研究更具有实际意义[23-24].
目前,混沌同步研究中最常见的方法是直接研究驱动-响应混沌系统对应的误差系统的稳定性,这样就将同步问题转变成稳定性问题来研究.因此,分数阶混沌系统的同步往往与其误差系统的稳定性密切相关.近年来,关于分数阶混沌系统同步控制的研究[22-30]大多都是基于传统的Lyapunov稳定性理论,通过对受控分数阶误差系统进行稳定性判断,从而实现驱动-响应系统的同步控制.然而,文献[31]中指出利用传统的Lyapunov稳定性理论在论证分数阶系统轨迹对滑模面的收敛性时是不恰当的,而利用分数阶稳定性理论会更合适.最近,文献[32-33]提出了针对分数阶非线性系统的Mittag-Leffler稳定性理论及分数阶Lyapunov方法,为分析分数阶混沌系统同步控制的稳定性提供了潜在的有效方法.
在上述文献研究的基础上, 本文主要研究了基于自适应滑模控制的不确定分数阶混沌系统同步问题.首先将分数阶微积分应用到滑模控制中,构造了一个具有分数阶积分项的滑模面,并利用分数阶非线性系统Mittag-Leffler稳定性理论证明了对应的滑模运动模态的稳定性.针对系统不确定及外界干扰项,基于分数阶Lyapunov稳定性理论与自适应控制方法,设计了一种滑模控制器以及分数阶次的参数自适应律,实现了两分数阶混沌系统的同步控制,并辨识出相应误差系统中不确定项及外界干扰项的边界.通过理论分析和数值模拟仿真验证了所设计的控制器的有效性和可行性.
1 预备知识
1.1 分数阶混沌系统与同步问题描述
考虑含不确定性及干扰项的分数阶混沌系统如下:

(1)

将系统(1)看作驱动系统,则对应的响应系统可表示为:

(2)
其中,y=(y1,y2,…,yn)T是系统(2)的状态向量,g(y)为系统的非线性项,Δg(y)为系统不确定性项,d(t)为外界干扰项,u(t)为控制输入.
为了提出新的设计理论和方法,需要做如下的假设:
假设1 假设Δf(x)、Δg(y)、c(t)及d(t)均为有界函数,并且存在合适的正常数μ和σ满足:

(3)
其中,μ和σ均为未知正常数.
我们定义如果存在一个控制输入u(t)使得
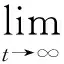
(4)
其中e(t)=(e1,e2,…,en)T为驱动系统与响应系统的状态误差,那么就可以说明驱动系统(1)和响应系统(2)实现了同步.因此,我们就将两混沌系统的同步问题转化为误差系统的稳定性问题,即利用控制函数u(t)使误差e(t)趋于0.由驱动系统(1)和响应系统(2)可以得到误差系统为:

c(t)+u(t)
(5)
本文主要针对误差系统(5)设计合适的控制器方案,通过判断误差系统(5)的稳定性来实现驱动系统(1)和响应系统(2)的同步控制.
1.2 分数阶微积分概述
定义1 函数f(t)的分数阶积分式定义[34]为:
(6)
其中t0≥0,α>0,且Γ(·)为伽马函数.
定义2 函数f(t)的Caputo分数阶导数定义[34]为:
(7)
由于Caputo分数阶微分定义的拉普拉斯变换所需初值与整数阶微积分的拉普拉斯变换相同,其几何和物理意义明确,在工程实际等广泛应用.因此下文中均采用Caputo定义.
与指数函数ez在整数阶微分方程中的作用相似,Mittag-Leffler函数在分数阶微积分中同样具有相当重要的作用.
定义3 双参数的Mittag-Leffler函数[35]可以表示为:
(8)
其中α>0,β>0,z∈C.
当β=1时,Eα(z)=Eα,1(z).特别地,E1,1(z)=ez.
考虑上述双参数,Mittag-Leffler函数的拉普拉斯变换可以表示为:

(9)
其中,t和s分别为时域和频域变量,Re(s)为s的实数部分.


(10)
那么,我们认为该系统的解是Mittag-Leffler稳定(渐近稳定)的.
其中,λ>0,b>0,α∈(0,1),且m(x)≥0在x∈Rn上满足Lipschitz条件.

V(x,t)≥γ(‖x‖),
DαV(x,t)≤0
(11)
其中,x⊂D,<α<1.如果D=Rn,那么该系统在xeq=0处是渐近稳定的.
引理3[37]令x(t)∈R为一个连续且可导的函数.则对于任意时刻t≥t0,都有:

(12)

2 同步控制器设计及稳定性分析
2.1 滑模面设计及稳定性分析
为了针对误差系统(5)设计合适的滑模控制器,我们首先构造一个具有分数阶积分项的滑模面如下:

(13)
其中,ai为正常数,0 Dqsi(t)=Dqei(t)+aiei(t) (14) 当误差系统(5)在滑模面运动时,滑模面及其分数阶导数需要满足: si(t)=0,Dqsi(t)=0 (15) 依据上述滑模面可达条件,我们可以得到对应的滑模运动模态如下: Dqei(t)=-aiei(t) (16) 这里,我们需要证明滑模运动模态(16)的渐近稳定性,以此保证从任意初值出发的受控误差系统(5)的轨迹在到达滑模面后渐近收敛到滑模面s(t)=0. 定理1 滑模运动模态(16)是渐近稳定的,当t→∞时,处在滑模面上的误差系统(5)的状态变量及轨迹也将渐近收敛到零点. 证明:选择如下形式的Lyapunov函数: (17) 对式(17)两边同时取q阶分数阶导数,可以得到: (18) 根据文献[39]中的结论,我们可以得到: (19) 将式(16)代入式(19)中,可以得到: (20) DqV1(t)+λV1(t)+M(t)=0 (21) 对式(21)进行拉普拉斯变换,可以得到: sqV1(s)-sq-1V1(0)+λV1(s)+M(s)=0 (22) (23) 进一步对式(23)进行拉普拉斯逆变换,可以得到: (24) 由于M(t)和tq-1Eq,q(λtq)均为非负函数,式(24)可简化近似为: V1(t)≤V1(0)Eq(-λtq) (25) 2.2 同步控制器设计及稳定性分析 由于在工程等实际应用中,系统不确定性项Δf(x)、Δg(y)及外界干扰c(t)、d(t)均为边界未知的,这里我们利用自适应控制法来解决这一问题.根据假设1,为了使误差系统(5)的运动轨迹收敛到所设计的滑模面并始终停留在滑模面上,我们设计的自适应滑模控制器如下: ui=fi(x)-gi(y)-aiei- (26) (27) (28) 定理2 基于假设1和滑模面方程(13),受控误差系统(5)在滑模控制器(26)和自适应率(27)、(28)的控制作用下,其运动轨迹将在有限时间内渐近地收敛到滑模面. 我们选择如下形式的Lyapunov函数: (29) 显然上述Lyapunov函数V满足引理2中的条件.利用引理3,对式(29)关于时间取q阶分数阶导数可得: (30) 将控制器(26)代入到上式(30)中,可以得到: (31) 将上式(31)化简得到: ≤-ρ≤0. (32) 根据式(32)所得结果,我们可以假设存在一个非负函数M(t)满足如下等式: DqV(t)+ρ+M(t)=0 (33) 对式(33)两边进行拉普拉斯变换,可以得到: (34) (35) 进一步对式(35)进行拉普拉斯逆变换,可以得到: (36) (37) 根据引理4可知,函数V(t)时单调非递增的,我们可以得到V(0)-V(t)≥0.因此,由上述不等式(37)可以得到 (38) 从上述不等式(38)可以清楚地得到,受控误差系统(5)的运动轨迹是在有限时间内到达滑模面的. 为了验证所提理论结果的正确性和有效性,我们分别选取分数阶Chen系统、分数阶Lorenz系统及分数阶Liu系统进行数值模拟,利用本文所提出的分数阶自适应滑模控制器,在系统含不确定性及外界干扰的情况下,分别实现相同分数阶混沌系统及不同分数阶混沌系统之间的同步. 3.1 分数阶Chen系统的自适应滑模控制同步 含系统不确定性项及外界干扰的分数阶Chen系统表示为: Dqx1=a(x2-x1)+Δf1+c1, Dqx2=(c-a)x1-x1x3+cx2+Δf2+c2, Dqx3=x1x2-bx3++Δf3+c3 (39) 其中,a=35,b=3,c=28,0 Dqy1=a(y2-y1)+Δg1+d1+u1, Dqy2=(c-a)y1-y1y3+cy2+Δg1+d1+u2, Dqy3=y1y2-by3+Δg1+d1+u3 (40) 其中,系统不确定性项及外界干扰项函数分别假定为Δg1=0.3sin(y1)cos(y2),d1=0.2sin(3t),Δg2=0.1cos(y1)cos(y3),d2=0.3cost,Δg3=0.2sin(y2)sin(y3),d3=-0.1cos(5t),u1,u2,u3分别为控制函数(26)的形式. 则误差系统可以表示为: Dqe1=a(e2-e1)+Δg1-Δf1+d1-c1+u1, Dqe2=(c-a)e1+ce2-x1e3-y3e1+Δg2- Δf2+d2-c2+u2, Dqe3=x1e2+y2e1-be3+Δg3-Δf3+d3-c3+u3 (41) 从数值模拟结果可以看出,在t=5s时加入控制后,e1,e2,e3在较短的时间内很快趋近于零,滑模面函数si(t)也很快地趋近于零,各控制器参数也趋近于某一定值,表明受控误差系统(41)的状态变量在所设计控制器(26)的作用下,很快地渐近收敛到零点并保持稳定.结果表明在系统含不确定性及外界干扰的情况下,驱动系统(39)和响应系统(40)能够实现同步,所提出的方法取得了较好的控制效果. 图1 误差系统(41)同步误差随时间的变化Fig. 1 Timehistory of synchronized errors of the error system (41) 图2 误差系统(41)各参数及滑模面函数随时间的变化Fig. 2 Time history of the control parameters and sliding surfaces of the error system (41) 3.2 分数阶Lorenz系统与分数阶Liu系统的自适应滑模控制同步 含系统不确定性项及外界干扰的分数阶Lorenz系统表示为: Dqx1=-a(x1-x2)+Δf1+c1, Dqx2=rx1-x2-x1x3+Δf2+c2, Dqx3=-bx3+x1x2+Δf3+c3. (42) 其中,a=10,r=28,b=8/3,0 Dqy1=a(y2-y1)+Δg1+d1+u1, Dqy2=by1-y1y3+Δg2+d2+u2, (43) 其中,a=10,b=40,c=2.5,d=4,0 则误差系统表示为: Dqe1=10e2-10e1+Δg1-Δf1+d1-c1+u1, Dqe2=40y1-y1y3-28x1+x1x3+x2+Δg2- Δf2+d2-c2+u2, Δf3+d3-c3+u3 (44) 从数值模拟结果可以看到,在t=5s时加入控制后,误差变量e1,e2,e3在较短的时间内很快趋近于零,滑模面函数si(t)也很快地趋近于零,各控制参数也趋近于某一定值,表明受控误差系统(44)的状态变量在所设计控制器(26)的作用下,很快地渐近收敛到零点并保持稳定.结果表明在系统含不确定性及外界干扰的情况下,分数阶Lorenz系统(42)和分数阶Liu系统(43)能够实现同步,所提出的方法取得了较好的控制效果. 图3 误差系统(44)的同步误差随时间的变化Fig. 3 Timehistory of synchronized errors of the error system (44) 图4 误差系统(44)各参数及滑模面函数随时间的变化Fig. 4 Time history of the control parameters and sliding surfaces of the error system (44) 本文基于分数阶Lyapunov稳定性理论,设计了一种滑模同步控制器和分数阶参数自适应律, 实现了含系统不确定项及外界干扰项的分数阶混沌系统的同步,并辨识出相应误差系统中不确定项及外界干扰项的边界.所提出的控制器针对不确定分数阶混沌系统,具有较好的同步控制效果和较强的抗干扰能力.文中构造的具有分数阶积分项的滑模面为分数阶混沌系统的滑模控制研究提供了一定的参考价值.同时,在分数阶系统稳定性分析中使用的分数阶Lyapunov稳定性理论及相关函数也可以很好地运用到其它分数阶系统同步控制方法中. 1 Petráš I. A note on the fractional-order cellular neural networks. In: The 2006 IEEE International Joint Conference on Neural Network Proceedings. Vancouver, Canada, IEEE, 2006:1021~1024 2 Bagley R L, Calico R A. Fractional order state equations for the control of viscoelastically damped structures.JournalofGuidance,Control,andDynamics, 1991,14(2):304~311 3 Sun H H, Abdelwahab A A, Onaral B. Linear approximation of transfer function with a pole of fractional power.IEEETransactionsonAutomaticControl, 1984,29(5):441~444 4 Dadras S, Momeni H R. Control of a fractional-order economical system via sliding mode.PhysicaA:StatisticalMechanicsanditsApplications, 2010,389(12):2434~2442 5 Engheia N. On the role of fractional calculus in electromagnetic theory.AntennasandPropagationMagazine, 1997,39(4):35~46 6 Metzler R, Klafter J. The random walk′s guide to anomalous diffusion: afractional dynamics approach.PhysicsReports, 2000,339(1):1~77 7 Tavazoei M S, Haeri M. Chaos control via a simple fractional-order controller.PhysicsLettersA, 2008,372(6):798~807 8 Grigorenko I, Grigorenko E. Chaotic dynamics ofthe fractional Lorenz system.PhysicalReviewLetters, 2003,91(3):034101 9 Gao X, Yu J. Chaos in the fractional order periodically forced complex Duffing′s oscillators.Chaos,Solitons&Fractals, 2005,24(4):1097~1104 10 Petráš I. A note on the fractional-order Chua′s system.Chaos.Solitons&Fractals, 2008,38(1):140~147 11 Tavazoei M S, Haeri M, Attari M, et al. More details on analysis of fractional-order van der Pol oscillator.JournalofVibrationandControl, 2009,15(6):803~819 12 Lu J G, Chen G. A note on the fractional-order Chen system.Chaos.Solitons&Fractals, 2006,27(3):685~688 13 Chen M, Han Z. Controlling and synchronizing chaotic Genesio system via nonlinear feedback control.Chaos.Solitons&Fractals, 2003,17(4):709~716 14 Chen B M, Lee T H, Peng K, et al. Composite nonlinear feedback control for linear systems with input saturation: theory and an application.IEEETransactionsonAutomaticControl, 2003,48(3):427~439 15 Radwan A G, Moaddy K, Salama K N, et al. Control and switching synchronization of fractional order chaotic systems using active control technique.JournalofAdvancedResearch, 2014,5(1):125~132 16 Mahmoudian M, Ghaderi R, Ranjbar A, et al. Synchronization of fractional-order chaotic system via adaptive PID controller.NewTrendsinNanotechnologyandFractionalCalculusApplications.SpringerNetherlands, 2010:445~452 17 Kamocki R. On the existence of optimal solutions to fractional optimal control problems.AppliedMathematicsandComputation, 2014,235:94~104 18 Ladaci S, Charef A. On fractional adaptive control.NonlinearDynamics, 2006,43(4):365~378 19 Shi B, Yuan J, Dong C. On fractional model reference adaptive control.TheScientificWorldJournal, 2014,7:521625 20 Razminia A, Baleanu D. Complete synchronization of commensurate fractional order chaotic systems using sliding mode control.Mechatronics, 2013,23(7):873~879 21 Yin C, Dadras S, Zhong S, et al. Control of a novel class of fractional-order chaotic systems via adaptive sliding mode control approach.AppliedMathematicalModelling, 2013,37(4):2469~2483 22 Dadras S, Momeni H R. Fractional terminal sliding mode control design for a class of dynamical systems with uncertainty.CommunicationsinNonlinearScienceandNumericalSimulation, 2012,17(1):367~377 23 Yin C, Zhong S, Chen W. Design of sliding mode controller for a class of fractional-order chaotic systems.CommunicationsinNonlinearScienceandNumericalSimulation, 2012,17(1):356~366 24 Faieghi M R, Delavari H, Baleanu D. A note on stability of sliding mode dynamics in suppression of fractional-order chaotic systems.Computers&MathematicswithApplications, 2013,66(5):832~837 25 Delavari H. A novel fractional adaptive active sliding mode controller for synchronization of non-identical chaotic systems with disturbance and uncertainty.InternationalJournalofDynamicsandControl, 2015:1~13 26 曹鹤飞,张若洵. 基于滑模控制的分数阶混沌系统的自适应同步. 物理学报, 2011,60(5):121~125 (Cao H F, Zhang R X. Adaptive synchronization of fractional-order chaotic system via sliding mode control.ActaPhysicaSinica, 2011,60(5):121~125 (in Chinese)) 27 潘光,魏静. 一种分数阶混沌系统同步的自适应滑模控制器设计. 物理学报,2015,64(4):40505~040505 (Pan G, Wei J. Design of an adaptive sliding mode controller forsynchronization of fractional-order chaotic systems.ActaPhysicaSinica, 2015,64(4):40505~040505 (in Chinese)) 28 Yuan J, Shi B, Ji W. Adaptive sliding mode control of a novel class of fractional chaotic systems.AdvancesinMathematicalPhysics, 2013,(4):594~603 29 Lin J S, Yan J J. Adaptive synchronization for two identical generalized Lorenz chaotic systems via a single controller.NonlinearAnalysis:RealWorldApplications, 2009,10(2):1151~1159 30 Tian X, Fei S, Chai L. Adaptive control of a class of fractional-order nonlinear complex systems with dead-zone nonlinear inputs. In: The 33rd Chinese Control Conference, Nanjing, China, IEEE, 2014: 1899~1904 31 Chen L, Wu R, He Y, et al. Adaptive sliding-mode control for fractional-order uncertain linear systems with nonlinear disturbances.NonlinearDynamics, 2015,80(1-2):51~58 32 Li Y, Chen Y Q, Podlubny I. Mittag-Leffler stability of fractional order nonlinear dynamic systems.Automatica, 2009,45(8):1965~1969 33 Li Y, Chen Y Q, Podlubny I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag-Leffler stability.Computers&MathematicswithApplications, 2010,59(5):1810~1821 34 Kilbas A A, Srivastava H M, Trujillo J J. Theory and applications of fractional differential equations. Amsterdam: Elsevier Science Limited,2006 35 Podlubny I. Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Pittsburgh: Academic Press,1998 36 Zhang F, Li C, Chen Y Q. Asymptotical stability of nonlinear fractional differential system with Caputo derivative.InternationalJournalofDifferentialEquations, 2011:635165 37 Aguila-Camacho N, Duarte-Mermoud M A, Gallegos J A. Lyapunov functionsfor fractional order systems.CommunicationsinNonlinearScienceandNumericalSimulation, 2014,19(9):2951~2957 38 Yu J, Hu C, Jiang H, et al. Projective synchronization for fractionalneural networks.NeuralNetworks, 2014,49(1):87~95 39 Zhang S, Yu Y, Hu W. Robust stability analysis of fractional-order hopfield neural networkswith parameter uncertainties.MathematicalProblemsinEngineering, 2014,(4):1~14 40 Diethelm K, Ford N J, Freed A D. A predictor-corrector approach for the numerical solution of fractional differential equations.NonlinearDynamics, 2002,29(1-4):3~22 *Project supported by the National Natural Science Foundation of China (Grant Nos. 11272242,11472202) and the Project Supported by Natural Science Basic Research Plan in Shaanxi Province of China (Grant Nos. S2014JC12575). † Corresponding author E-mail: wying36@163.com 30 November 2015,revised 20 March 2016. A METHOD OF ADAPTIVE SLIDING MODE CONTROL FOR SYNCHRONIZATION OF ONE CLASS OF UNCERTAIN FRACTIONAL-ORDER CHAOTIC SYSTEMS* Li Te Yuan Jianbao Wu Ying† (StateKeyLaboratoryforStrengthandVibrationofMechanicalStructure,SchoolofAerospace,Xi′anJiaotongUniversity,Xi′an710049,China) For one class of fractional-order chaotic system with systematic uncertainties and external disturbances, firstly, fractional calculus is applied into sliding controller, and a sliding surface with a fractional integral term is designed. Based on the theory of fractional Lyapunov stability and adaptive control,a sliding mode controller with the fractional-order adaptive laws of the parameters is proposed to achieve the synchronization of two uncertain fractional-order chaotic systems emphasizing the systematic uncertainties and the external disturbances, and the bounds of uncertainty and the disturbance in corresponding error system are estimated. It should be pointed out that the fractional Lyapunov stability theorem and functions introduced in the stability analysis of the fractional-order chaotic systems can be applied to many other control methods for fractional-order nonlinear systems. Finally, numerical examples are given to verify the effectiveness and feasibility of the proposed control method. systematic uncertainty, sliding mode control, fractional adaptive law, Lyapunov stability theorem *国家自然科学基金(11272242,11472202)和陕西省自然科学基础研究计划资助项目(S2014JC12575) 10.6052/1672-6553-2016-026 2015-11-30收到第1稿,2016-03-20收到修改稿. † 通讯作者 E-mail: wying36@163.com.
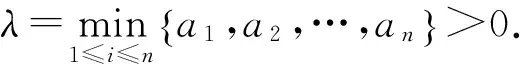
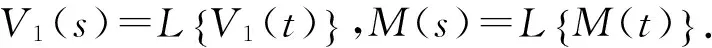
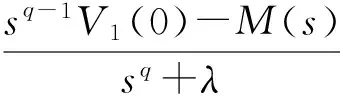
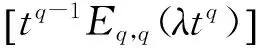
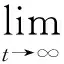











3 数值仿真







4 结论
