基于UKF参数估计的地月自由返回轨道设计

张洪礼，韩潮，胡雯婷

（1. 北京航空航天大学 宇航学院，北京 100191；2. 北京机电工程研究所，北京 100074）

基于UKF参数估计的地月自由返回轨道设计

张洪礼1,2，韩潮1*，胡雯婷2

（1. 北京航空航天大学 宇航学院，北京 100191；2. 北京机电工程研究所，北京 100074）

为快速简便地设计地月自由返回轨道，提出了一种基于UKF参数估计算法的地月自由返回轨道设计方法。该算法不仅避免了传统数值方法推导相关梯度矩阵的复杂性，而且只需基于地月系统二体模型给出猜测初值，从而显著降低了自由返回轨道设计的难度，将地月自由返回轨道对应的两点边值问题的求解转化为参数估计问题，该算法可以得到高精度模型下收敛的精确解。数值仿真结果表明：该算法结构简洁，求解效率较高，所得结果精确且具有良好的鲁棒性，可以作为地月自由返回轨道设计的一个有力工具。

地月自由返回轨道；微分修正法；无迹卡尔曼滤波；参数估计

0 引 言

自20世纪的探月工程开始，地月自由返回轨道就受到了广泛关注。当故障发生时自由返回轨道提供了乘员救生的机会，对当前及未来的探月任务具有重要的工程意义。最早的3次阿波罗任务就采用了自由返回轨道，对保证任务的成功起了重要作用。

从Apollo时代起，很多学者致力于地月系统中自由返回轨道的研究。Schwaniger利用圆形限制性三体系统的镜面对称原理，研究了具有对称特性的自由返回轨道[1]，但该方法局限于对称自由返回轨道。Jesick和Ocampo在此基础上研究了对称自由返回轨道的设计方法，并使用多点打靶和序列二次规划对其进行了优化，但这种方法计算量比较大，并且仍然局限于对称自由返回轨道[2]。Green提出了一种基于初始设计搜索自由返回轨道精确解的梯度法[3]，但此方法收敛性能不佳，并且需要人工干预。Miele利用镜像特性和微分修正法，研究了月球和火星任务的自由返回轨道的最优化问题[4]。Peng引入优化算法，提出了基于PSO和SQP算法的串行轨道设计策略，并对自由返回轨道的全局特性进行了研究，但求解效率不能令人满意[5]。Luo提出了一种基于伪状态理论的地月自由返回轨道设计方法，这种方法与基于圆锥曲线拼接的方法相比，能够极大提高初始设计解的精度，但相对来说比较复杂[6]。

地月自由返回轨道设计本质上是一个两点边值问题，一般的求解过程分为2步：首先通过解析方法和简化的地月系统动力学模型得到设计初值；然后采用数值方法或优化算法搜索完整动力学模型对应的精确解。对于自由返回轨道，由于模型的敏度和非线性程度非常高，对猜测初值的精确度和精确解求解算法的收敛性都提出了苛刻的要求。在地月自由返回轨道设计中，微分修正法是最常用的精确解求解方法，但在实际应用中会遇到一定困难。考虑到模型对初值的高度敏感性，通常需要良好的初值，作为迭代求解精确解的基础。但是在不清楚解空间结构的情况下，很难通过简单的方法获得良好的初值。

为了解决上述的问题，本文提出一种基于UKF参数估计算法（UPE）的地月自由返回轨道设计方法。该方法通过生成采样点高效地估计Jacobian矩阵，从而避免了微分修正法等传统数值方法推导相关梯度矩阵的复杂性。另外，由于该方法具有大范围收敛特性，从而只需基于地月系统二体模型给出猜测初值，就可以通过若干迭代获得收敛的精确解，从而极大地降低了自由返回轨道设计的难度。因此，该方法可用来高效准确地设计地月自由返回轨道。

1 问题描述

1.1 动力学模型

在初值设计时，本文使用二体模型。二体模型是地月系统最简单的近似模型，该模型略去其它天体引力对探测器运动的影响，探测器只在地心引力场内运动，月球是绕地心做约束圆周运动的空间几何点，这样就把地月转移轨道设计问题转化为在地球引力场中的探测器-月球交会或拦截问题。

在精确解求解时，本文使用高精度轨道预报模型。除了考虑地球和月球的中心引力，同时考虑地球的J2项非球形摄动、太阳的第三体引力和太阳光压摄动，其中，太阳和月球的真实空间位置通过DE405星历获取，太阳光压摄动模型选为圆柱阴影模型，光压系数选为1.95，光照面积选为20 m2。

1.2 约束分析

对于自由返回轨道，给定起始时刻和转移时间时，整条轨道就由初始状态决定。工程实际情况中，自由返回轨道的设计需要满足施于3个特殊点上的一系列约束条件，即起始点、近月点和再入点。

在起始点，奔月轨道倾角是由发射场决定的，奔月轨道起始点地心距是根据运载的能力或停泊轨道确定，一般要求起始点为近地点。在近月点，为保证良好的观测条件，并且能完成近月点制动，近月点月心距和到达近月点时间一般是给定的。在再入点，为满足再入时的热防护需求，再入角有严格的限制，而再入点地心距是根据稠密大气层的高度确定的。为了确保问题有解，对再入时间没有严格的要求，并且通过调整转移起始时间等其他参数来满足再入倾角和着陆场的限制。

2 初值设计

地月系统最简单的近似模型是二体模型，在二体模型下，探测器的轨迹为地心圆锥曲线，即开普勒轨道。关于开普勒轨道的两点边值问题一直以来受到人们的关注，其中Lambert问题是最受人关注的问题之一，在近地和深空轨道设计中都得到了成功的应用。

在地月转移轨道设计中，经常遇到另一种开普勒轨道的两点边值问题，要求根据给定的起始点的径向距离和飞行方向角、终止点的径向距离，求解一条在给定飞行时间内从起始点转移到终止点的开普勒轨道，例如地月自由返回轨道设计中对起始点飞行方向角和再入角的约束，这类问题被称为约束起始点飞行方向角的类Lambert问题，往往比经典的Lambert问题更为复杂。Luo提出了一种解决此问题的有效方法[7]，本文利用其中的计算方法给出自由返回轨道的初值。

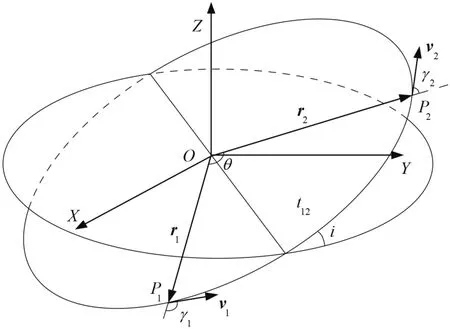
图 1 约束起始点飞行方向角的类Lambert问题Fig. 1 Quasi-Lambert’s problem with fixed flight-path angle constraint

首先，根据约束分析，给定起始点的地心距R0和飞行方向角γ1、地月转移时间TE2L和转移起始时间T0，如从近地点出发，则γ1=π/2，由T0和DE405星历可以得到地月距RL，问题归结于求解对应的约束起始点飞行方向角的类Lambert问题，如图 1所示。利用相关文献中的方法，就可以求得一条满足条件的奔月轨道，这实际上是一条对称的自由返回轨道[；最后，可以进]一步求得迭代变量的初值w0=vTLI,0ΩTLI,0ωTLI,0T，其中vTLI,0、ΩTIL,0、ωTLI,0分别为起始点的近地点速度、升交点赤经、近地点幅角，作为下一步利用UKF滤波器进行参数估计的基础。

3 精确解求解方法

在初值的基础上w0，进一步研究通过数[值方法搜索高精度轨道预报模型下的精确解对于自由返回轨道，自由变量选为：w= [vTLIΩTLIωTLI]T，约束条件为

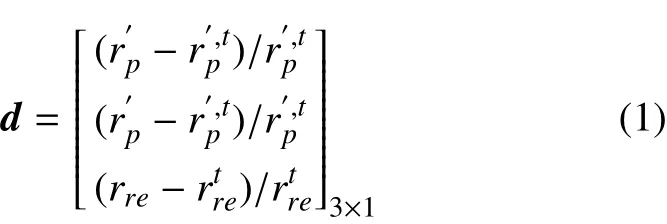
d被看作w经过非线性映射后的输出，即：

其中：F为打靶函数，实际上是从初始状态到末端状态的积分。

该问题本质上是求解一个具有三个变量和三个方程的非线性方程组F(w)=0，即寻找某个向量w∗使得F(w∗)=0。微分修正法是常用的求解非线性方程组的方法之一，迭代公式如下S={Wiχi}，使得它们的平均值等于wk，方差等于Pwk。接下来，对每个采样点进行非线性映射F，以获得新的一组投影点L={Wi,di}。输出的估计平均值dk和方差Pdkdk可以通过求投影点的带权重的平均值和方法近似获得。这样，通过以下UPE方法的迭代过程，可以获得迭代序列{wk}

本文提出一种基于UKF参数估计的算法来求解该问题。不同于微分修正法，把w看成平均值wk和方差Pwk的三维随机变量。然后，选择一组带权重的采样点

其中：Kk是卡尔曼增益矩阵。通过逐步更新wk，序列{dk}逼近于零，当和足够接近于零，认为满足施加的约束，此时的即为精确解。整个迭代过程如图 2所示，尽管形式上与微分修正法类似，但UKF方法本质上是不同的，是基于概率理论的。

图 2 UKF参数估计示意图Fig. 2 UKF parameter estimation

将原问题改写为状态空间表达式为

其中：w为待估计参数；d为输出，期望值为零；F为非线性测量；rk~N(0, Rr)为系统噪声；ek~N(0, Re)为测量噪声。

对于该确定性问题，rk和ek应该设为零，但考虑到保证数值稳定性，Rr和Re通常设为小值。这样，UPE算法可以用来求解待估计参数，如图 3所示，关于UPE算法的详细描述可参见文献[8]。尺度因子决定了采样点的分布大小，一般设为[10−4,1]，β考虑了w的先验分布，一般设为0，一般有两种常用的更新方法，其中η∈[0,1]，ρRLS∈(0,1]。UPE算法的计算复杂度受采样点的个数影响很大，当给定待估计参数的维度后，由采样策略唯一确定。考虑到地月自由返回轨道设计的高度非线性，本文选择将超球形单形采样[9]和比例采样[10]结合起来作为采样策略。通过将原问题进行合适的单位化处理，可以增强求解问题的稳定性，因此在本文研究的算例中，所有自由变量和约束条件都被处理为个位数的量级，以提高数值搜索的稳定性。

图 3 UKF参数估计流程图Fig. 3 UKF-PE flowchart

4 数值仿真

针对以上轨道设计方法，下面考虑一组仿真算例，对比微分修正法和UPE方法在地月自由返回轨道设计中的表现。本文中的微分修正法采用了目前应用最广泛的拟牛顿法-Broyden方法，并不需要推导Jacobian矩阵。由于地月几何关系对自由返回轨道设计的影响很大，本文选择了月球公转周期中的4个特殊算例，如表 1所示。

首先，通过求解相应的类Lambert问题，4个算例的初值可以在地月二体模型下生成，如表 2所示。实际上，对于每个算例都存在2个初值，分别对应着地球顺行出发和地球逆行出发2种情况。不失一般性，本文只讨论地球逆行出发这种情况。

在初值基础上，微分修正法和UPE方法用来搜索收敛精确解。迭代停止条件选为

表 1 初始条件Table 1 Initial conditions

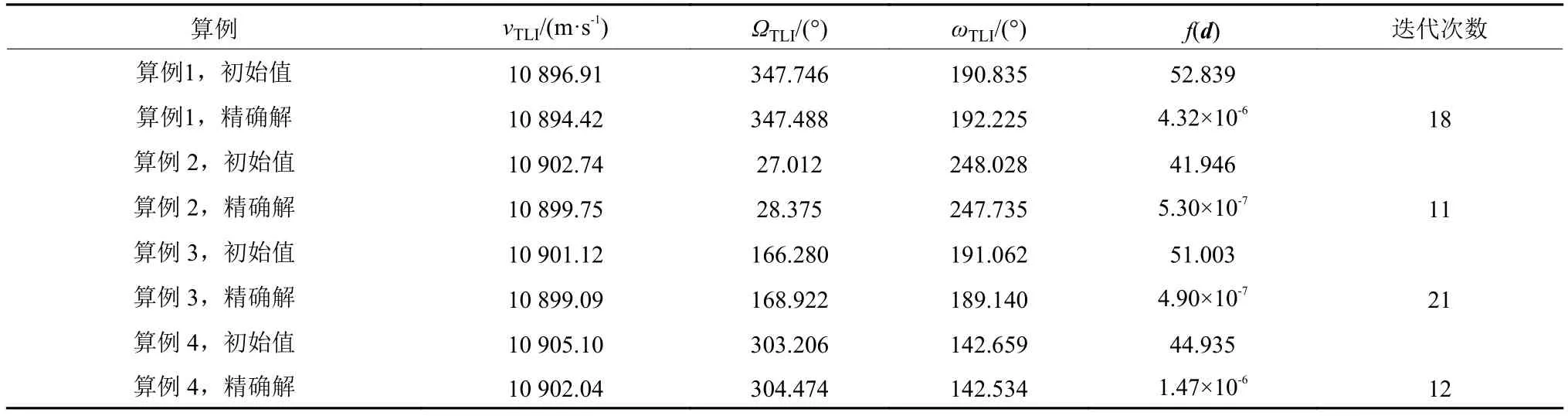
表 2 UPE方法的求解性能Table 2 Targeting performance of UPE

其中ε=10−5。另外，每种方法的最大迭代次数为300。对于UPE方法的详细设置，Pw0设为I，R0r设为10–4I，R0

e设为10–20I，W0设为0.5，尺度因子α设为5×10−4，β设为0，权重因子η设为0.5。微分修正法对于上述4个算例都无法获得收敛的精确解，而UPE方法可以通过若干迭代后搜索到收敛的精确解并且获得稳健的收敛表现。初值（IE）、最终解（FS）、约束函数值（f(d)）、迭代次数（Iter）如表 2所示，目标参数的误差如表 3所示。

从表 2可以看出，UPE方法可以在30步之内搜索到精确解，并且表现了良好的收敛特性。从表 3可以看出，高度的误差小于15 m，飞行方向角的误差小于10–4（°），这表明约束条件得到了很好的满足。因此，UPE算法在地月自由返回轨道设计中的有效性得到验证。

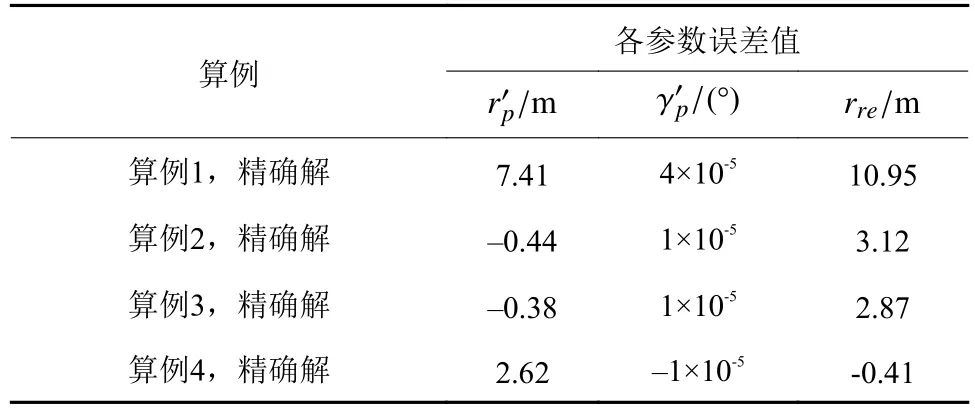
表 3 目标参数误差Table 3 Errors of the targeting parameters of UKF-PE

为了进一步研究UKF参数估计算法的收敛域，对于该算例最终解的某一个分量添加扰动，而另外两个分量保持不变。从这个扰动点出发，分别使用微分修正算法和UKF参数估计算法来搜索转移轨道的精确解，不断增加扰动量，一直到精确解搜索过程发散，由此得到这2种算法对于特性的扰动分量的收敛域，2种算法的收敛域统计如表 4。

从表 4可以看出，自由变量的单个分量收敛域与约束条件之间没有特定的规律，而仅仅有很大的变化区间，体现了该问题收敛域具有十分复杂的几何结构，这也是由于自由返回轨道的高度非线性特性导致的。另外，UKF参数估计算法的收敛范围比微分修正算法更大，在最差的情况，微分修正法的和的收敛域只有约1°，这意味着需要非常好的初值。根据进一步的算例验证，对于地月自由返回轨道设计问题，在平均水平上，UKF参数估计算法的收敛域是微分修正算法收敛域的10~15倍。

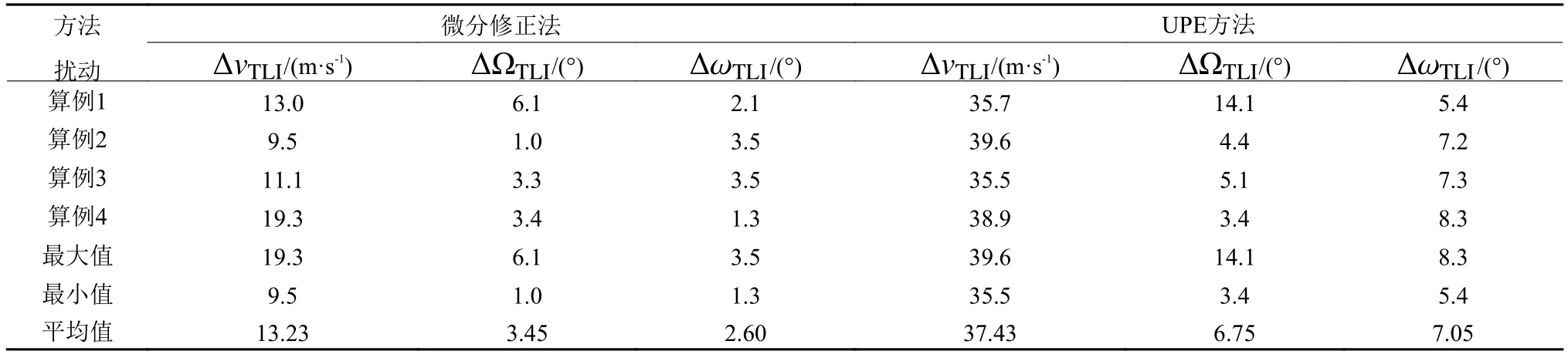
表 4 一维搜索空间中的收敛域对比Table 4 Convergence domains in the one-dimensional search space

5 结 论

本文提出了一种基于UKF参数估计的从初步设计到高精度设计的地月自由返回轨道设计方法。该方法只需要利用地月二体模型给出的初值，同时避免了传统数值方法对梯度矩阵的推导，因此极大地降低了自由返回轨道设计的难度。利用该方法求解得到的自由返回轨道，可以很好地满足探月任务的各类约束条件。数值仿真表明：该方法具有收敛域广、收敛速度较快、鲁棒性好等优点。因此，该方法可以作为地月自由返回轨道设计的一个有力工具。

[1]Schwaniger A J. Trajectories in the earth-moon space with symmetrical free return properties, Technical Note D-1833[R]. [S. l]：National Aeronautics and Space Administration，1963.

[2]Jesick M，Ocampo. Automated generation of symmetric lunar freereturn trajectories[J]. Journal of Guidance，Control，and Dynamics，2011，34（1）：98-106.

[3]Green B S，LewinN. A gradient method for obtaining circumlunar trajectories[C]// AIAA Astrodynamics conference. [S.l]：AIAA，1963.

[4]Miele A，Wang T，Mancuso S. Optimal free-return trajectories for moon missions and mars missions[J]. Journal of the Astronautical Sciences，2000，48（2-3）：183-206.

[5]Peng Q B，Shen H X，Li H Y. Free return orbit design and characteristics analysis for manned lunar mission[J]. Science China Technological Sciences，2012，54（12）：3243-3250.

[6]Luo Q，Yin J，Han C. Design of earth-moon free-return trajectories[J]. Journal of Guidance，Control，and Dynamics，2012，36（1）：263-271.

[7]Luo Q，Meng Z，Han C. Solution algorithm to a quasi-lambert's problem with fixed flight-direction angle constraint[J]. Celestial Mechanics and Dynamical Astronomy，2011，109（4）：409-427.

[8]Haykin S. Kalman filtering and neural networks[M]. New York：John Wiley &Amp Sons Inc，2001.

[9]Julier S J. The spherical simplex unscented transformation [C]//Proceedings of the American Control Conference. Denver，Colorado：[s. n.]，2003.

[10]Julier S J. The scaled unscented transformation[C]//Proceedings of the American Control Conference. Anchorage：[s. n]，2002.

通信地址：北京航空航天大学宇航学院新主楼B1110室（100191）

电话：（010）82316536

E-mail：zhanghongli@buaa.edu.cn

Design of Lunar Free-Return Trajectories Based on UKF Parameter Estimation

ZHANG Hongli1,2，HAN Chao1*，HU Wenting2
（1. School of Astronautics, Beihang University, Beijing 100191, China；2. Beijing Institute of Mechanical and Electrical Engineering, Beijing 100074, China）

A fast and convenient design-method based on UKF parameter estimation is proposed for lunar free-return trajectories. The method proposed avoids calculating the Jacobian matrix and obtains large convergence ability compared with the common differential-correction method. Given that the initial estimate of the free-return trajectory is generated under the two-body Earth-spacecraft model, the difficulty of guessing a good initial estimate is greatly reduced. Through solving the converted parameter estimation problem using the method proposed, the converged final solution can be found under a high-fidelity gravitational model by a few iterations. Despite its simplicity, the method is proves to be quite effective in finding the solution of lunar free-return trajectories with great numerical accuracy.

lunar free-return trajectories；differential-correction method；unscented Kalman filter；parameter estimation

V412.4

A

2095-7777（2017）02-0178-06

10.15982/j.issn.2095-7777.2017.02.012

张洪礼（1988– ），男，博士生，主要研究方向：航天器轨道动力学与仿真。

[责任编辑：宋宏，英文审校：朱鲁青]

张洪礼，韩潮，胡雯婷. 基于UKF参数估计的地月自由返回轨道设计[J]. 深空探测学报，2017，4（2）：178-183.

Reference format: Zhang H L，Han C，Hu W T. Design of lunar free-return trajectories based on UKF parameter estimation [J]. Journal of Deep Space Exploration，2017，4（2）：178-183.

2015-09-20

2015-12-02