叠加法在基础力学教学中的应用
2017-07-03何芝仙樊清华
何芝仙,樊清华
(安徽工程大学 建筑工程学院,安徽 芜湖 241000)
[教育·教学]
叠加法在基础力学教学中的应用
何芝仙,樊清华
(安徽工程大学 建筑工程学院,安徽 芜湖 241000)
针对基础力学的教学内容,讨论了叠加法在基础力学中应用的典型实例如求结构的约束反力、求解单自由度振动系统在任意激励力作用下的响应、画梁的弯矩图、求梁的弯曲变形、广义胡克定律计算公式的推导以及求解组合变形问题等。论述叠加法求解基础力学问题的适应条件和相对统一的求解一般步骤,结论是符合叠加法求解适应条件的问题,应用叠加法求解优势显著,基础力学教学应对叠加法给予足够的重视。
线性问题;叠加原理;适应条件;求解一般步骤
0 引 言
基础力学是高等学校工科本科专业的必修专业基础课,我校工科各专业的基础力学主要包含理论力学和材料力学。叠加原理是求解线性问题的一个非常重要的原理,应用叠加原理求解线性问题的方法即谓叠加法。基础力学中的大多数问题属于线性问题,因而叠加法在基础力学中的应用十分广泛。 材料力学教科书中有关“叠加法求梁的变形”通常这样叙述“当梁上同时作用几个载荷时,可分别求出每一个载荷单独作用时所引起的变形,然后将所求得的各个变形代数相加,即为这些载荷共同作用 时 的 变 形 ”[1]。 一 般 地 ,构 件 或 结 构 在 多 个 载 荷 同时作用下引起的响应(如约束反力、变形、应力等),应等于每一个载荷单独作用下引起的响应的和,这就是所谓的叠加法。应用叠加法求解一般步骤可以归纳为以下3步:
1.按照结构上作用的主动力将具有多个主动力同时作用的求解问题分解成只有一个主动力作用的基本单元;
2.求解基本单元的响应;
3.叠加。
基础力学中应用叠加法求解问题应满足的条件:
1.所求解的问题必须是线性问题,非线性问题叠加原理不成立;
2.在一个主动力作用下基本单元的求解应简单快捷;
3.主动力个数不宜过多,一般不宜超过 3 个。 过多的主动力会导致基本单元的求解以及叠加时计算量增加,计算出错几率增加。
基础力学中许多问题,应用叠加法求解方便快捷,有些问题甚至可以达到通过心算直接写出求解结果的神奇程度。
1 叠加法在理论力学中的应用
1.1 叠加法求约束反力
根据作用在研究对象(结构、构件)上的主动力,求解约束反力,是理论力学中刚体静力学的主要 目 的[2]。 图 1 为 具 有 集 中 力 和 均 布 力 同 时 作 用 的简支梁,其支座 A,B 处的约束反力为 FA和 FB,参见图 2(a)。 根据叠加法的求解一般步骤,首先将其分解成只有分布力q和只有集中力P作用的基本单元;求解基本单元,得到相应的 A,B 处的约束反力为; 叠加后支座 A,B 处的约束反力为这类问题由于基本单元的约束反力可以通过观察心算得到, 利用叠加法求解在省略中间过程后,可以直接写出求解结果,非常适合采用叠加法求解。文 献[3]给 出 了 一 个 利 用 叠 加 法 求 解 多 刚 体 系 统 平 衡问题的例子,如图 3所示。 尽管可以采用叠加法求解出各个约束处的约束反力,但由于主动力数量较多且在一个主动力作用下的基本单元的约束反力求解并不简便,故采用叠加法求解该问题的优势已丧失殆尽。
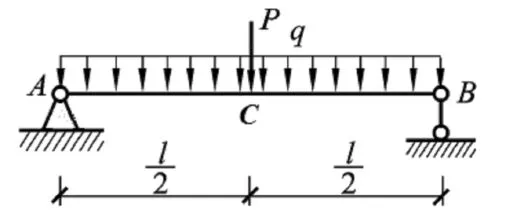
图1

图2
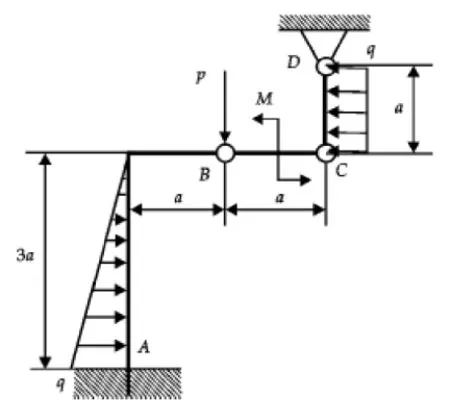
图3 多刚体平衡问题

图4 任意激励力
1.2 叠加法求解单自由度振动系统在任意激励力作用下的响应
单自由度振动系统在任意激励力作用下的响应求解问题,是一个典型的动力学问题。 其运动微分方程为

式中:m 为质量,c 为阻尼,k 为弹簧刚度系数,f(t)为任意激励力。
Duhamel在研究该问题时,巧妙地运用叠加法,得到一个完美的解答,即所谓 Duhamel积分。 其基本思路是:
1.t时刻系统的响应只取决于 t时刻以前的作用力。 在[0,t]时间段的任意激励力 f(t)可视为一系列元冲量 f( )d 组成,如图 4 所示。
2. 元冲量 f ( )d 引起的系统的动力响应为dx( ,t),可解出
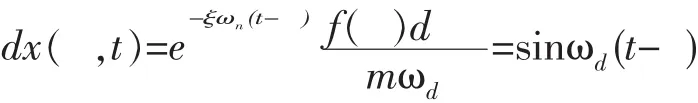
3.根据叠加原理,t时刻系统的动力响应 x(t)等于 t时刻以前的元冲量 f( )d 引起的系统的动力响应 dx( ,t)的和,即

这就是 Duhamel积分。
2 叠加法在材料力学中的应用
材料力学在小变形条件下所研究的问题都是线性问题,满足叠加原理的条件,故叠加法在材料力学中应用十分广泛,如叠加法画弯矩图、求梁的弯曲变形、广义胡克定律计算公式的推导、组合变形的求解等表现出独特的求解优势。
2.1 叠加法画弯矩图
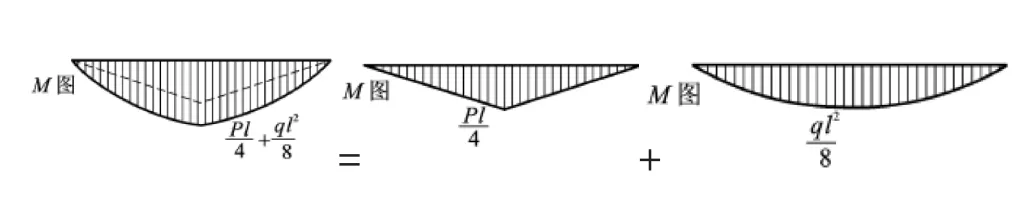
图5 叠加法画弯矩图
尽管可以应用叠加法画梁的剪力图,但求解方法并无优势,而采用叠加法画图 2(a)所示的简支梁弯矩图,则十分方便快捷,其求解过程如图 5 所示。与求解约束反力的过程类似,只不过此时的求解目标是梁的弯矩图。由于本例中基本单元的求解结果一目了然,应用叠加法画其弯矩图也可以达到直接给出结果的境界。
2.2 叠加法求梁的弯曲变形
材料力学中应用叠加法与查表法相结合,可以有效地求解梁指定截面的位移与转角。对于少学时的材料力学教学,由于学时不足不能介绍能量法求梁的弯曲变形,这种方法就显得尤其重要。图 1 所示的简支梁中点 C 的竖向位移,根据叠加原理,可以表达为

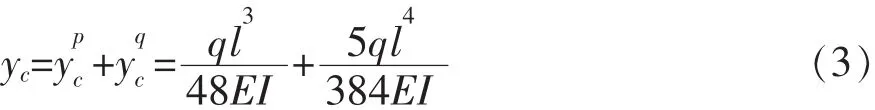
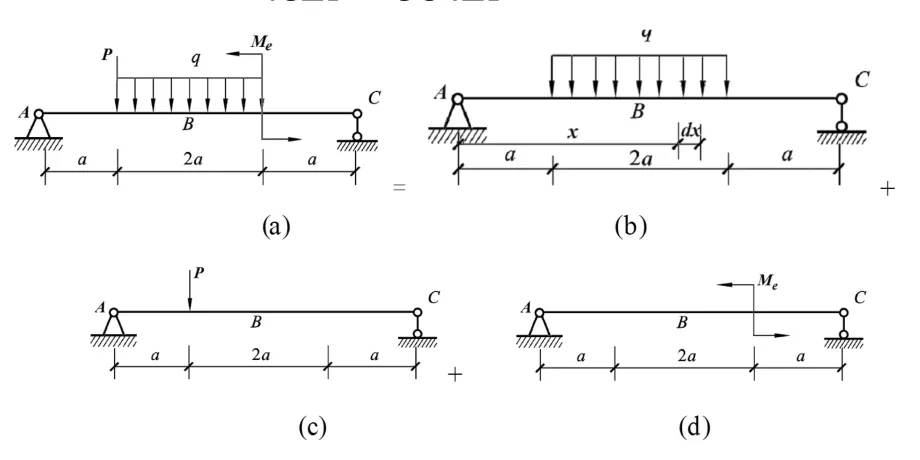
图6 叠加法求梁的弯曲变形
图6(a)所示的受到比较复杂载荷作用的简支梁,欲求中点 B 截面的挠度,可以将其分解成分布力、集中力和集中力偶单独作用的基本单元,如图 6(b)(c)(d),则根据叠加原理,中点 B 截面的挠度为

式中:yB为简支 梁 在 集 中 力 P 单 独 作用引 起的B 截 面 的 挠 度 , 由 查 表 法 可 得e为简支梁在集中力偶 Me单独作用引起的 B 截面的挠度为简支梁在均布力 q单独作用引起的 B 截面的挠度。 为了进一步求出,在距支座 A 为 x 处取 dx微段, 在 qdx 作用下 B 截面的挠度为,根据叠加原理和结构对称性代入(4)从而有
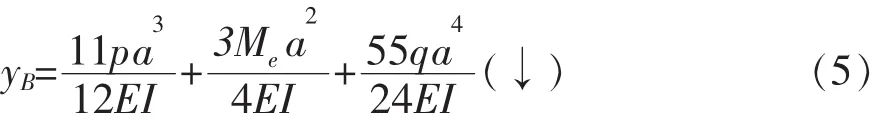
该例两次应用叠加原理求出了受载比较复杂的梁指定截面上的挠度,解法优势显著。 与积分法相比, 叠加法避免了求解挠曲线近似微分方程,只做了加减和积分运算,降低了运算级别,节省了大量的计算时间。 与图乘法相比,叠加法由于利用了查表法直接得到了基本单元的挠度,从计算工作量上看,仍具有一定的优势。 值得一提的是,叠加法求梁的弯曲变形,由于最后的结果为代数相加,对作用在梁上载荷的数目并无限制。
2.3 叠加法推导广义胡克定律计算公式
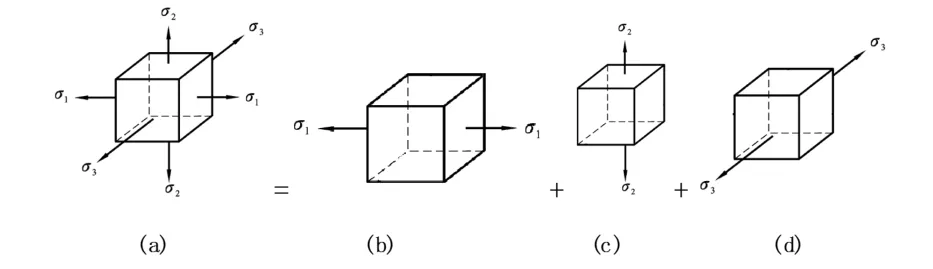
图7 叠加法推导广义胡克定律计算公式
图7(a)为具有 3 个主应力的主单元体,利用叠加法推导广义胡克定律计算公式十分方便。首先将其分解成只有一对主应力作用的基本单元,如图7(b)(c)(d)。在只有一对主应力作用下引起的 3 个主方向的应变可表示为
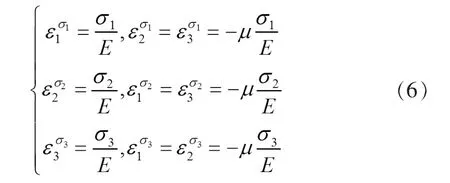
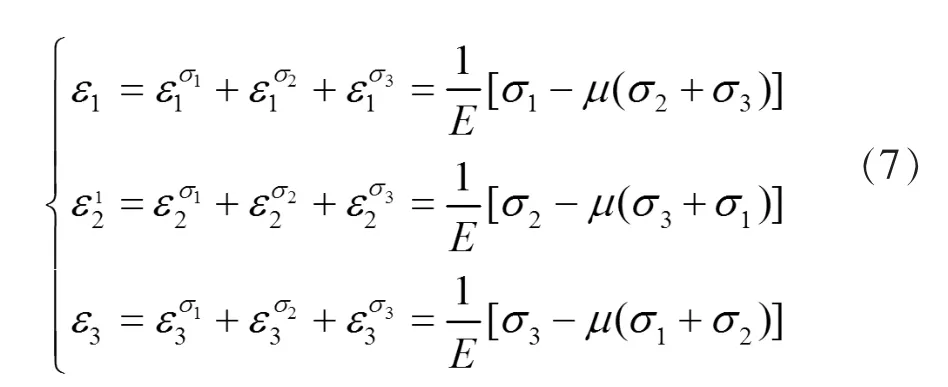
即用主应力表示的广义胡克定律。
2.4 组合变形
叠加法在材料力学中的一个重要的应用,就是建立组合变形构件的强度条件和刚度条件。承受组合变形的构件,受载复杂、组合方式多样,求解的关键就是掌握以叠加原理为基础的求解方法。叠加法将组合变形分解成基本变形,求解分解后的基本变形的应力和变形,最后通过叠加得到组合变形的求解结果,是一个应用叠加法解决材料力学问题的生动实例。 以图 8(a)所示的弯扭组合变形为例,说明其求解步骤。
1.载荷分解,将组合变形分解成若干个基本变形。 从图 8(b)所示知,所讨论的问题为弯曲与扭转组合变形。
2. 按基本变形求解每组载荷作用下的内力、应力、 位移。 力偶Me引起的扭矩图和横力F作用引起的弯矩图参见图 8(c)及(d),对应的应力分布见图 8(e)。
3.叠加求出组合变形的解。如图 8(e)所示,危险点 a 点弯曲正应力为, 扭转切应力由于危险点a点的弯曲正应力和扭转切应力方向不同,本质上应为矢量相加,即求出主应力

若采用第 3强度理论,建立的强度条件为:
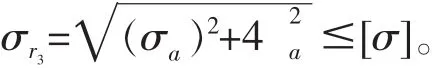
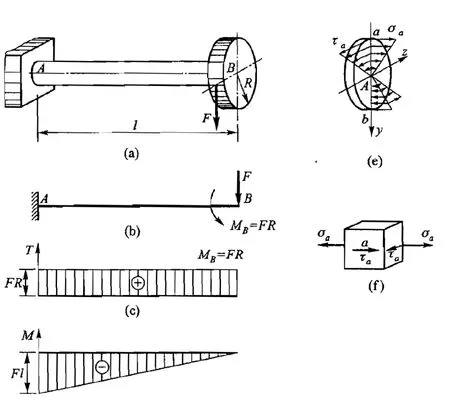
图8 弯扭组合变形
3 结 论
叠加法在基础力学中应用广泛,是基础力学中解决工程问题的一个十分有效的手段,基础力学教学中应给予足够的重视。 采用叠加法求解问题,应注重其适应条件,即所求解的问题为线性问题,基本单元的求解应简单快捷,最后的叠加求和也应容易实现。符合叠加法求解条件的基础力学中的问题,采用叠加法求解优势显著。如求解结构的约束反力、求解单自由度系统在任意激励力作用下的响应、画弯矩图、求梁的弯曲变形、广义胡克定律计算公式的推导以及求解组合变形等。特别是对于Duhamel积分的推导、组合变形的求解等这些问题,叠加法提供了求解问题的最具特色的可行方法。叠加法有相对统一的求解步骤即按照求解已知量与未知量关系分解成基本单元、求解基本单元、叠加。基础力学的教学中应对叠加法给予足够的重视。
[1]孙训方,方孝 淑,关来泰.材料力 学(I,II)(第 5 版)[M].北 京:高等教育出版社,2009:164-167.
[2]哈尔滨工 业大学理论 力学教研室.理论 力学(I,II)(第 7 版 )[M].北京:高等教育出版社,2009:45-49.
[3]杨立军,张勇.叠加原理在刚体静力 学中的应用[J].陕西科 技大学学报,2005,23(2):70-72.
[4]梁秋道.略论“叠 加法”在材料 力学中的应 用[J].洛阳大学学报,1995,10(4):49-53.
责任编辑:胡德明
The Application of Superposition Method in the Teaching of Basic Mechanics
He Zhixian,Fan Qinghua
(School of Architectural Engineering,Anhui Polytechnic University,Wuhu 241000,China)
In this paper,the application of superposition method in basic mechanics is illustrated by typical examples,involving seeking the constraints of a structure,solving the response of a single degree of freedom vibration system applied on arbitrary exciting force,drawing the bending moment diagram of a beam,computing the bending deformation of a beam,deriving generalized Hooke's law and solving combined deformation problems,etc.The suitable condition and general steps to solve problems with superposition method are discussed.The results show obvious advantages of superposition method in solving problems in basic mechanics when the problems meet the suitable condition.Superposition method should be given enough attention in the course teaching of basic mechanics.
linear problem;superposition principle;suitable condition;general steps to solve problems
G642
:A
:1672-447X(2017)03-0100-04
2017-03-01
安徽省教育厅重点教研项目(2015jyxm17)
何芝仙(1963-),博士,安徽工程大学教授,研究方向为基础力学的教学科研工作。
