装备自主定点精确投放的轨迹修正研究

许 飞，许世蒙，杜建华，曹贻鹏

(装甲兵工程学院 a.基础部； b.科研部， 北京 100072)



【基础理论与应用研究】

装备自主定点精确投放的轨迹修正研究

许 飞a，许世蒙a，杜建华b，曹贻鹏a

(装甲兵工程学院 a.基础部； b.科研部， 北京 100072)

对军用装备的投放过程建立偏微分方程组模型，确定满足投放要求的最佳投放位置和投放速度，分析了在投放位置和投放速度均存在合理误差的情况下，落地点的区域范围，并进一步对投放轨迹进行修正，以减少由于投放位置和投放速度的误差对投放精度的影响，通过采用蒙特卡罗方法进行仿真模拟，结果表明，该偏微分方程组模型以及通过对装备投放轨迹修正更加有利于实现对投放过程的精确控制。

偏微分方程；轨迹修正；投放精度；蒙特卡罗法

装备空投是指利用降落伞将人员和装备投送到指定地点以实现快速作战的一种技术，是实现兵力、装备、补给等快速、精确送达的有效手段[1]，但其受投放位置、投放速度、风速等因素影响较大，造成投放精度不高、落点分散、收集困难、损耗偏高，并且随着新军事思想研究的不断深入，未来军用装备的空投环境将更加恶劣，在一些极端天气或能见度很低的情况下，装备空投可能无法实施，因此，研究无人引导军用装备自主定点精确投放在现代战争中的应用尤为重要。

为此，本研究从装备空投的建模和仿真两个方面进行研究，首先采用偏微分方程组[2]对空投过程建立模型，确定满足投放要求的最佳投放位置和投放速度，并在投放位置和投放速度均存在误差的情况下，分析装备的投放精度，同时对投放轨迹进行修正，其次通过采用蒙特卡罗法对投放过程进行仿真模拟，结果表明，能够显著提高装备定点投放精度，有利于进一步研究投放轨迹的多次调整甚至实时调整。

1 模型建立与变量动态分析

1.1 装备投放过程分析及建模

装备空投过程在垂直方向分为3个阶段：① 降落伞打开前，装备作变加速运动；② 降落伞打开后，装备作变减速运动直至匀速运动；③ 装备作匀速运动至安全着落。在水平方向，装备始终在作变减速运动直至达到安全着落速度，即5 m/s以下。忽略降落伞完全开伞以及控制器调节轨迹所需时间。

假定装备质量、重力及阻力分别为mw、Gw、Dw，降落伞的质量、重力及阻力分别为ms、Gs、Ds，投放速度为V1=(vx,vy,0)，实时速度为Vk=(vx,vy,vz)，位移向量为S=(Sx,Sy,Sz)。根据装备受力情况，以时间t和轨迹修正参数h为参量建立偏微分方程组模型：

(1)

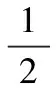
(2)

(3)

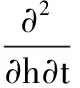
(4)

max(Vkx,Vky,Vkz)≤V0

(5)

(6)

在式(1)～式(4)中：λ为调节系数，当降落伞未打开时λ取0，打开后λ取1；τ(h)为修正函数，用于对投放轨迹与预设轨迹偏离一定误差时进行调整，式(5)与式(6)为约束条件；V0为安全落地速度；H为投放高度。

1.2 空投过程中变量的动态分析

1.2.1 气压、温度对空气密度的影响

影响空气密度的因素主要有压强和温度，其关系为[3]

(7)

p(h)=pone-1.26×10-4 h

(8)

k(h)=(1-6×10-4h)kon

(9)

式中：kon=293 K，为标准状态空气的温度；pon=101.325 kPa，为标准状态空气的压强；ρon=1.29 kg/m3，为标准状态空气的密度。

由式(7)～式(9)易知，在2 000 m高空空气密度最小，为1.007 4 kg/m3；在地面处空气密度最大，为1.289 8 kg/m3。由于相差不大，为了便于运算，这里取平均值ρ=1.142 8 kg/m3代替。

1.2.2 装备所受空气阻力的分析

装备和降落伞在空气中所受风阻取决于物体的形状、迎风面积、空气密度、风阻系数以及相对运动速度，其关系式为[2-3]

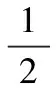
(10)

式中：f为空气阻力；c为风阻系数；s为迎风面积；v为装备相对风的速度；n的取值与装备运动速度有关，通常认为10 m/s 时n=1，10 ～311 m/s时n=2。

1.2.3 降落伞面积的选取

降落伞的面积越大，减速效果越好，但其外表面受到的风阻也就越大，不但会降低定点投放的精确度，增加装备搜寻的难度，也会为后续的投放轨迹修正带来不便；而降落伞的面积越小，也会影响装备的减速效果，为此，降落伞的选取应兼顾上述两个方面，采用适宜的降落伞进行投放，且在垂直方向受力均衡[4-5]，则

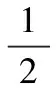
(mw+ms)g

(11)

式中：Dwz、Dsz分别为Dw、Ds在垂直方向上的分量值；c1、c2分别为降落伞和装备的风阻系数，根据文献[2]取c1=0.873，c2=1.28；s为降落伞面积；s2=22 m2为装备底部迎风面积，并假设装备质量为m=10 000 kg，通过式(10)可得降落伞面积为

s=7 826.1 m2

(12)

在此面积下，装备可减速至落地安全速度以下，并保持该速度直至降落至目标点,联合式(1)～式(12)得到装备运动微分方程组。

2 模型仿真及可靠性

利用Matlab软件，并采用蒙特卡罗法分别从无随机因素、有随机因素及对投放轨迹进行调整3个方面对装备投放过程进行仿真，结果表明：对投放轨迹进行调整能够极大修正由投放误差所引起的精确度降低的问题。

2.1 无随机因素下的Matlab仿真

2.1.1 Matlab仿真中的参数

假定装备投放高度为h=2 000 m，装备连同降落伞的质量为m=10 000 kg，装备底部、前方、侧面面积分别为s1=22 m2，s2=7 m2，s3=15 m2，装备投放时的速度为v=80 m/s，开伞时间为t=8 s，并忽略开伞对装备姿态的影响，在下降过程中装备受到水平风的影响，方向与装备滑行方向相反，且风力大小与装备所处高度有关，其关系为：U(h)=32.3-31.2e-1.256×10-4×h，h<10 000 m。

2.1.2 空投中高度、速度的实时变化曲线

由2.1.1中的参数设定，采用离散化的方法对投放过程进行Matlab仿真，可以得到装备空投过程中的实时高度和速度变化曲线。

图1是装备在水平风向状态下的投放轨迹，可以看到，降落伞打开的先后，装备的投放轨迹在1 700 m处有一个明显的突变，这是因为降落伞打开后带来较大的风阻，从而装备空投的加速度发生了较大的变化，从这刻开始，装备从变加速运动状态转为变减速运动状态，直至匀速运动至地面，从图1中还可以看到，落地点的坐标是(3 551.8，0)，装备在水平方向发生大的偏移，引起较大的投放误差，为装备的搜寻带来不便。

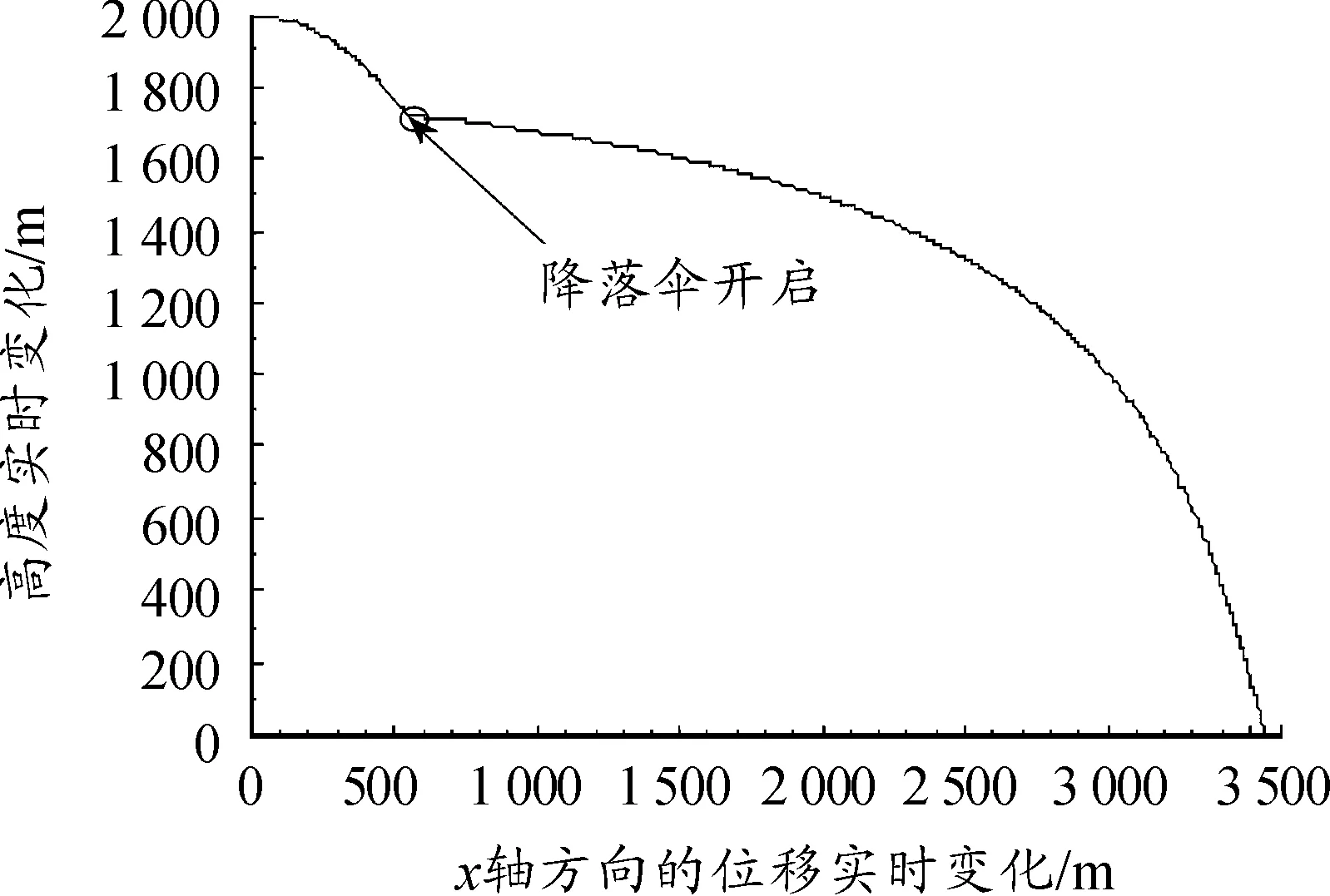
图1 空投过程中各方向位移实时变化

图2是装备空投过程中的速度实时变化，在垂直方向上，装备在很短时间内便降至5 m/s以下的安全速度，而在x轴方向，装备投放速度则变化的较为平缓，但在到达地面时，装备各个方向的速度均已降至安全速度以下[6]。

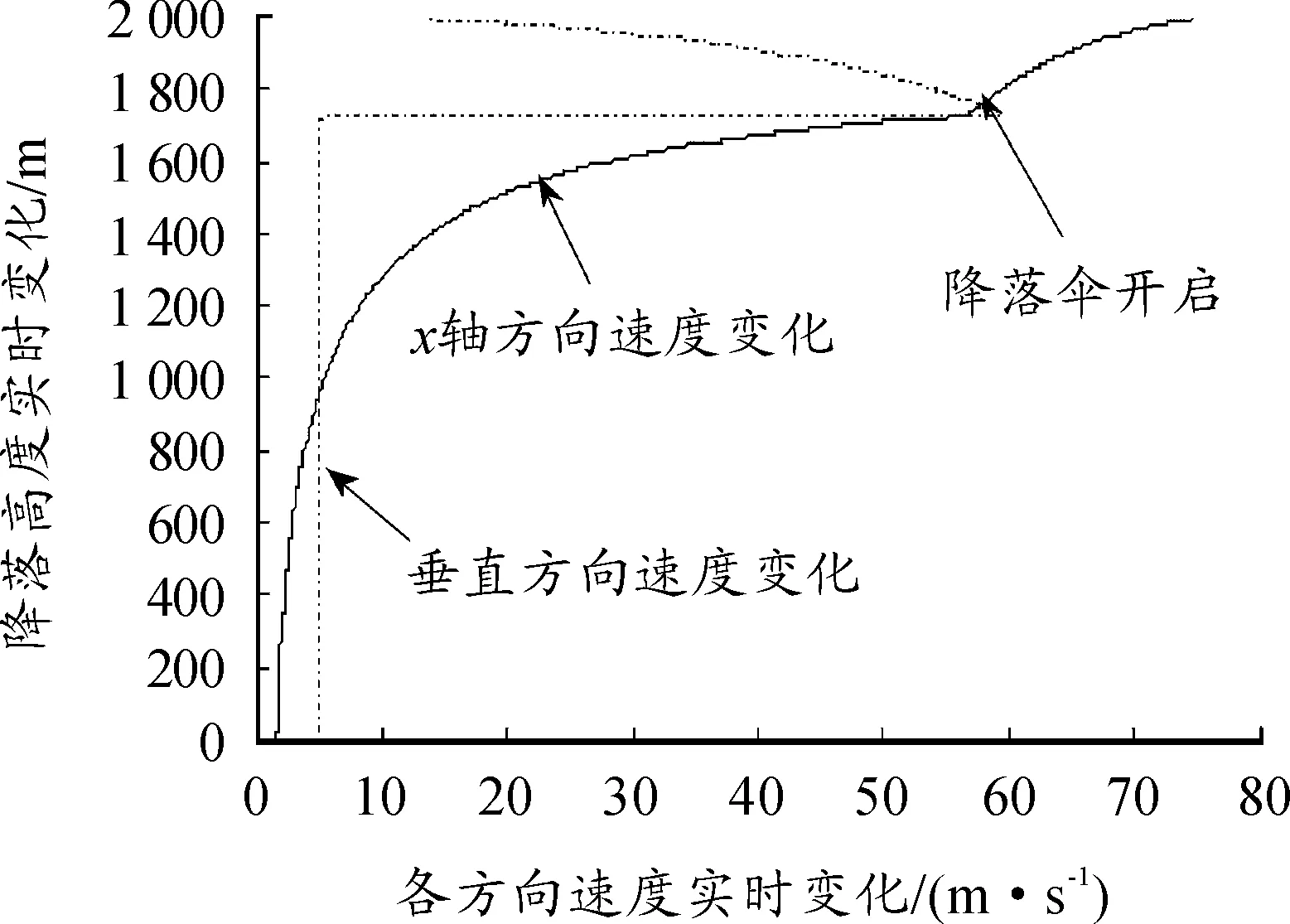
图2 空投过程中各方向速度实时变化

总之，装备投放的成功与否，不但要考虑空投的精确度，还要考虑装备空投的安全性，其中精确度的高低与装备在水平方向上的偏移有很大的关系，为此在水平方向上的轨迹调整对提高空投的精确度有着重要的意义。

2.2 添加了随机因素的Matlab仿真

2.2.1 装备空投误差设定及仿真分析

在实际的装备投放中，由于风速、风向及随机因素等影响，装备在空投位置及速度上存在一定的误差，从而使装备不能准确地落至预定点。现假定装备在投放位置的误差为10 m，投放速度的误差为10 m/s，风的方向水平不变，采用蒙特卡罗法模拟50次的空投过程[7]，其落点范围如图3所示。 图3显示出装备在投放时存在误差的情况下着落点的范围为[-10,10]×[3 350,3 750]，与理论落点坐标(3 551.8，0)对比来看，在y轴存在10 m的偏离，而在x轴则存在200 m的偏离，难以达到投放要求。若要提高装备空投的精确度，需要对空投轨迹进行调整。

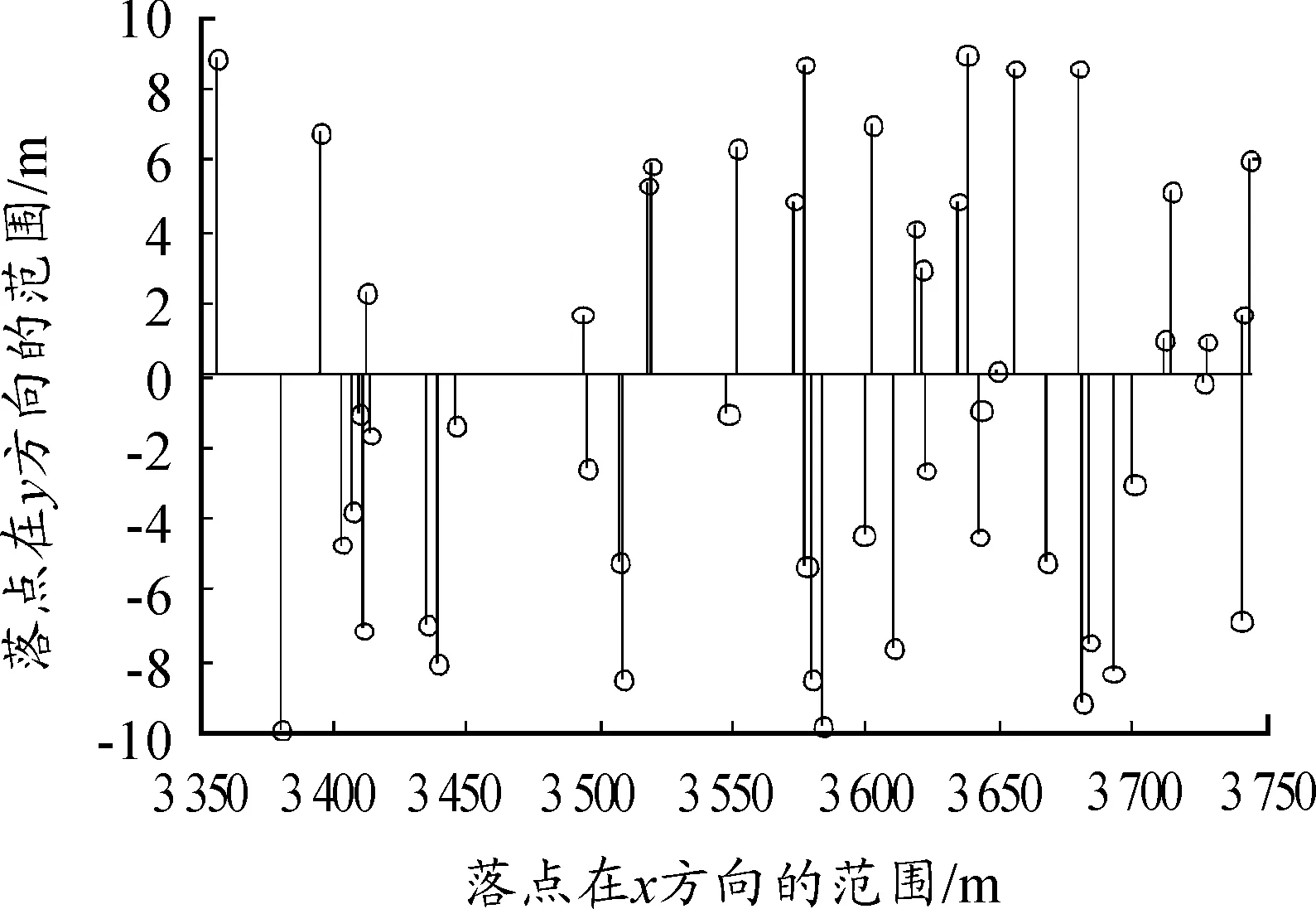
图3 装备着落点的范围

2.2.2 装备空投中的轨迹调整及仿真分析

空投轨迹调整的目标是实现准确、安全着陆，要求着陆点离目标点近、着陆速度小、控制能量在容许范围内[8-9]，调整频率可以一次、多次或实时调整，随着投放环境的不同，可以设计控制器进行自主判断调节的频率及强度，在本次仿真实验中，调整的频率为一次，调整的时机为装备在h=1 000 m处，忽略调整所需时间，具体调整过程如图4所示。

图4 投放轨迹修正流程

图4显示了装备空投轨迹调整的流程，是对1 000 m处空投状态的调整，实际中可以实时判断装备空投的轨迹状态并进行调整，从而保证装备空投的精确度，通过轨迹调整将大大提高空投的精确度，缩小装备散落范围，本次轨迹调整后的落点范围具体如图5所示。

图5 修正空投轨迹的装备着落点的范围

图5显示出轨迹调整后的装备着落点范围在y轴存在9 m 的偏离，在x轴则存在100 m的偏离，较未调整轨迹的投放范围有了明显的提升，但较实际作战仍有进一步提高精度的必要。

2.2.3 空投轨迹调整前后的对比分析

前两节从无随机因素影响、添加随机因素影响、对空投轨迹修正3个方面进行了仿真，主要目的是探索轨迹修正的参数设定及频率，其仿真对比结果如表1所示。

表1 轨迹调整后的仿真结果对比

从表中可以看到，经轨迹调整后的装备着落点范围的精确度提高了50%，投放的稳定性也有较大幅度的提升，但在实际的装备空投中，此投放效果还需进一步提高[10]，当然这完全可以通过调整轨迹修正的技术参数或增加轨迹修正的次数来满足要求，但如何设计轨迹调整的技术参数及合理的调整时间还有待进一步研究，本文是对上述问题的有益探索。

3 结论

对装备空投过程建立了偏微分方程组模型及进行了仿真模拟，并在装备投放过程中对空投轨迹进行了修正，通过采用蒙特卡罗法多次仿真模拟，结果表明，轨迹调整后的空投效果将大大提升，投放稳定性也得到进一步提高，但对不同环境下的轨迹调整的技术参数的设定和调整时间的选取，还有待进一步研究。

[1] 唐波，高军，李良春，等.精确空投系统投放点确定的辅助决策模型构建[J].装备指挥技术学院学报，2010，21(2)：123-125.

[2] 李薇，黄振华，周群，等.无风条件下军用装备定点投放的数学建模与仿真[J].火力与指挥控制，2012，37(10)：43-45.

[3] 许飞，许世蒙，杜建华，等.军用装备定点精确投放的建模与仿真[J].装甲兵工程学院学报，2016，30(1)：99-103.

[4] TANG Q G,ZHANG Q B.Perturbation Dynamics and Its Application for Parachute Munition System[J].Journal of China Ordnance，2007,3(4):272-274.

[5] ZHU Y，LIU L,WANG Z P.Flow Field Characteristics for Parachute-projectile System[J].Chinese Journal of Mechanical Engineering，2011,24(5):813-819.

[6] WANG H Y,HONG H J.Environment Adaptability Evaluation for Buffering Airbag of Heavy Equipment During Airdrop Landing[J].Journal of China Ordnance，2012,8(4):223-229.

[7] GUO Z,MIAO Q L.Prediction of the Trajectory of the Manned Spacecraft SHENZHOU-7 Deploying a Parachute Based on a Fine Wind Field[J].Science China Earth Science，2011,24(9):1413-1429.

[8] 郑成，吴庆宪，姜长生，等.基于IAGA的翼伞系统分段归航轨迹的优化[J].电光与控制，2011，18(2)：69-72.

[9] 胡海静,朱圣英,崔远平.基于Lyapunov函数的小天体软着陆障碍规避控制方法[J].深空探测学报,2015,2(2):149-154.

[10]胡容，姚敏，赵敏，等.翼伞精确空投系统归航轨迹规划与控制[J].指挥控制与仿真，2014，36(6)：111-116.

(责任编辑 杨继森)

Research on Trajectory Correction of Equipment with Autonomous Precise Fixed-Poinft Drop

XU Feia, XU Shi-menga, DU Jian-huab, CAO Yi-penga

(a. Department of Fundamental Courses; b. Department of Science Research, Academy of Armored Force Engineering, Beijing 100072, China)

A partial differential equations model is built for the drop process of military equipment, with which to determine the best placement and speed to meet the drop requirements, and discusses the regional scope of landing point in the case of reasonable error in the delivery point and speed, and corrects the drop trajectory in order to reduce the influence of drop precision by the error of delivery point and speed. Using the Monte Carlo method, we simulate the drop process. The results indicate that this partial differential equations model and the correction of the drop trajectory will help improve the accuracy of the delivery process and the drop effect significantly.

partial differential equation; trajectory correction; drop precision; Monte Carlo method

2017-03-02；

2017-03-25

国家自然科学基金资助项目(51675531)

许飞(1981—)，男，硕士，讲师，主要从事微分几何研究。

10.11809/scbgxb2017.06.036

format:XU Fei, XU Shi-meng, DU Jian-hua,et al.Research on Trajectory Correction of Equipment with Autonomous Precise Fixed-Point Drop[J].Journal of Ordnance Equipment Engineering,2017(6):165-168.

O175

A

2096-2304(2017)06-0165-04

本文引用格式：许飞，许世蒙，杜建华，等.装备自主定点精确投放的轨迹修正研究[J].兵器装备工程学报，2017(6):165-168.