基于矩估计/最小二乘法的杂波模型参数估计方法
2017-07-03吴元伟经富贵王李波
吴元伟,经富贵,2,王李波
(1.中国空空导弹研究院,河南 洛阳 471009; 2.航空制导武器航空科技重点实验室,河南 洛阳 471009)
【信息科学与控制工程】
基于矩估计/最小二乘法的杂波模型参数估计方法
吴元伟1,经富贵1,2,王李波1
(1.中国空空导弹研究院,河南 洛阳 471009; 2.航空制导武器航空科技重点实验室,河南 洛阳 471009)
针对传统杂波模型的参数估计方法无法兼顾计算效率和精度的问题,提出了一种基于矩估计和最小二乘法的杂波统计模型混合参数估计方法,以矩估计法得到模型参数的初始值,使用最小二乘法迭代优化得到参数估计的最终值,数字仿真的结果证明了此方法的有效性和准确性;该混合模型参数估计方法可以在计算量不大、原理简单的情况下实现模型参数的精确估计,且不局限于单一杂波模型的参数估计,具有很好的通用性和工程应用价值。
杂波分布模型;参数估计;矩估计;最小二乘法;混合估计
杂波统计模型的参数估计是杂波仿真、雷达信号处理与性能评估、目标检测与识别的基础[1-2]。根据雷达分辨率及地海面状况,地海杂波的统计分析可分别用瑞利(Rayleigh)分布模型、莱斯(Rice)分布模型、对数正态(Log-normal)分布模型、威布尔(Weibull)分布模型和K分布模型等来表示[3]。对不同的模型来说,杂波分布描述的准确性取决于对模型参数估计的正确性。
目前,常用的杂波统计模型参数估计方法包括矩估计法、最大似然估计法、混合估计法等[4-11]。其中矩估计法利用各阶矩的计算量与杂波幅度统计量的对比得到统计模型参数的估计值,计算方便,但精度较差;而最大似然估计是最优估计,精度高,但该方法对参数初始值敏感,且需要解高维非线性方程,计算过程复杂。常见的混合估计方法包括最大似然估计/矩估计法、矩估计/神经元网络法。相对于单一估计法,混合估计方法可在某些方面简化估计过程,提高计算精度,但仍然存在未解决:如最大似然估计/矩估计法无法避免求解非线性函数的问题;矩估计/神经元网络法虽然能很好的处理噪声问题、精度高且对初始值不敏感,但是需要较长的训练时间,实现难度较大。
针对传统估计方法无法兼顾计算效率和精度的问题,本文提出了一种基于矩估计/最小二乘法的杂波统计模型参数混合估计方法,即通过矩估计方法得到参数初始估值,再由最小二乘法对参数进行迭代优化得到精确的估计参数。数字仿真结果分析表明:该方法实现简单,精度较高,具有通用性,是一种实用的杂波统计模型参数估计方法,并且不限于特定杂波模型的参数估计。
1 算法原理
对于试验采集或仿真手段产生的雷达杂波数据,数据分析过程基于其概率密度分布的统计结果,设为p(x)。以下说明参数估计的算法流程,假设用以描述和分析数据的杂波统计模型分布的概率密度函数为f(x;a,b),其中(a,b)为模型的两个待估计参数。则有:
p(x) =f(x;a,b)
(1)
根据矩估计方法的原理,假设总体x的概率密度函数为x~f(x;θ1,θ2,…,θl),θ1,θ2,…,θl为l个待估参数。若总体x的k阶矩均存在,记为μk,则有:

(2)
将待分析数据作为数据总体x的样本,设其k阶矩为
(3)
由Ak=μk,在k≥l时可得到待估参数θ1,θ2,…,θl的矩估计量。矩估计方法计算简单方便,在模型参数估计中广泛应用。本文首先通过以上矩估计方法由式(1)得到各阶矩μk与参量a,b的关系式,并与式(2)联立形成包含k个方程的关于a,b变量的方程组,该方程的解作为杂波模型参数的值(a0,b0)。但此时计算的参数精度较差,需要进一步的优化。
将以上估计得到的参数(a0,b0)作为杂波模型参数的初始值,利用最小二乘法,控制参数的估计误差。根据最小二乘法的原理,设

[p(x)-f(x;a0,b0)]2=min
(4)
对f(x;a,b)进行泰勒展开至一阶,并由式(1),可以得到:
(5)
对式(4)变形得到:
(6)
以差分代替上式中的微分,即
(7)
最小二乘法是通过最小化误差的平方和找到实际数据的最佳函数匹配,可以简便地优化估计参数。使用多元回归的最小二乘算法,问题转化为求解使式(7)中误差函数最小的参数(a,b),采用基于梯度搜索的LMS算法求解参数,即可得到(Δa,Δb),进而得到杂波模型参数的修正值:
a1=a0+Δa;b1=b0+Δb
(8)
当误差(Δa,Δb)不满足阈值判断条件时,将修正值(a1,b1)返回,继续上述迭代优化过程,直到参数的修正值满足设置的误差阈值。
算法的流程图如图1所示。

图1 算法流程
1) 根据试验测量或者数字仿真的杂波数据,统计得到杂波概率密度函数p(x);
2) 使用矩估计的方法计算数据序列的各阶矩Ak,利用Ak与杂波模型的各阶矩μk的关系,计算参数的初始值(a0,b0);
3) 根据杂波模型参数现有估计值f(x;a0,b0),得到其余实测数据分布密度函数的差值p(x)-f(x;a0,b0)以及f(x;a0,b0)对应偏微分的近似值(差分);
4) 由最小二乘估计法的原理,结合式(7),计算杂波模型参数的修正量(Δa,Δb);
5) 判断修正量是否小于阈值ξ,如果大于阈值,重复3)~5)步骤;若修正量小于阈值,即得到杂波模型参数的最终估计值(a,b)。
对于待分析的杂波数据,在事先无法确定描述其概率密度分布的最佳模型的情况下,可利用上述方法对可能的杂波模型进行拟合。最后根据计算的结果,评估各种模型与数据的匹配度,选择出最佳的模型来描述相关数据,再进行后续的分析。
2 仿真验证
本文以K分布杂波为例,通过数字仿真说明上述杂波参数估计算法实现过程,验证其有效性。K 分布可以准确地描述高分辨雷达在低擦地角下回波幅度统计分布的拖尾现象,在雷达数据分析、地海杂波建模以及雷达信号检测与识别中具有广泛的应用,精确而快速的K分布模型参数估计方法一直是研究的热点。
2.1 K分布杂波模型
K 分布可以看作散斑分量(快变化分量)和基本幅度调制分量(慢变化分量)两个因子的乘积:前者表示大量散射体反射的相参叠加(服从Rayleigh分布),后者表示与地海大面积结构相关的散射束平均功率(服从Gamma分布),其概率密度函数为
(9)
其中, Γ(ν)为伽马函数,Kν-1为ν阶第二类修正贝塞尔函数,α为尺度参数,与杂波的强度相关,ν为形状参数。典型条件下K分布的概率密度函数如图2所示,由图2中可以发现由于概率密度积分的固定为1,因此ν越大,K分布的峰位越偏大,相同α条件下导致K分布越平缓,拖尾现象更明显;而α越大,幅度大杂波变多,相同ν条件下K分布越平缓。
使用矩估计方法,可以得到参数估计值为

=(E(x4)/2E2(x2)-1)-1
(10)
(11)
其中E(x4)与E(x2)分别为K分布的四阶矩/二阶矩样本的数量影响估值的精度。
2.2 仿真数据验证
为验证矩估计/最小二乘法混合估计算法,通过球不变随机过程法仿真得到了一组K分布杂波数据,其实部与虚部的数据如图3所示。

图2 典型的K分布概率密度函数

图3 K分布杂波数据

图4 杂波数据的概率密度函数与功率谱密度
根据算法流程,统计得到杂波概率密度函数p(x)如图4所示,并计算杂波数据的四阶矩/二阶矩。用矩估计方法根据式(10)、式(11)得到K分布参数估计初始值(v0,α0),按照本文混合估计方法的算法流程计算参数的估计值。设最小二乘法中误差的判断阈值为0.02,仿真过程中χ2随迭代次数变化情况如图5所示,从结果上看,本文提出的方法经过8次迭代就实现了数据收敛,计算的效率较高。

图5 χ2随迭代次数的变化
图6中虚线为矩估计方法得到的概率密度分布函数,与杂波数据的统计结果偏差较大;双划线为混合估计方法得到的概率密度分布函数,从中可以发现混合估计方法对杂波模型的参数进行了优化,使其能够准确地描述原始数据的统计结果。
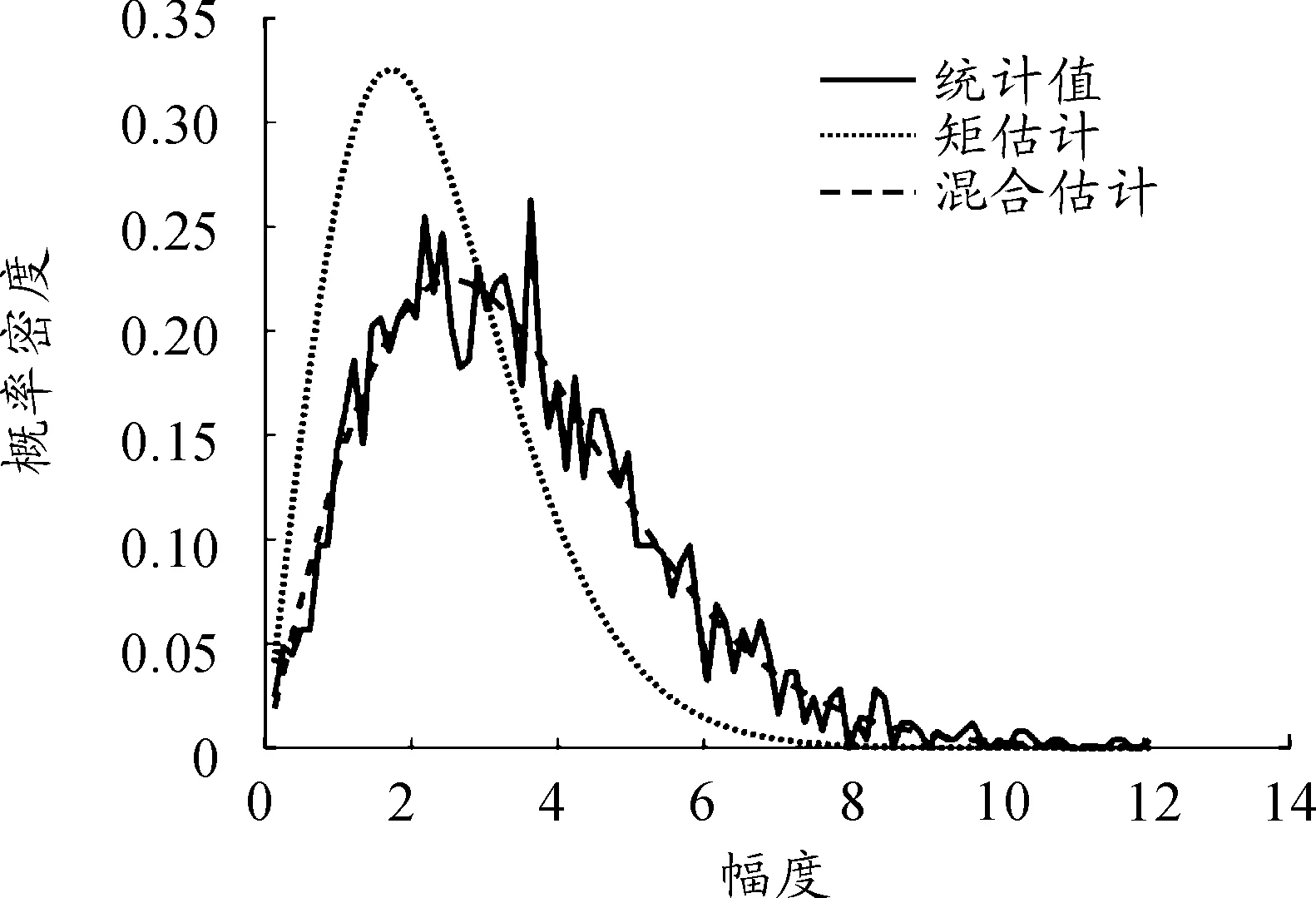
图6 不同估计方法得到的概率密度函数
3 结论
杂波统计模型的参数估计方法对杂波研究非常重要,本文提出了一种基于矩估计和最小二乘法的杂波统计模型混合参数估计方法,以矩估计法得到模型参数估计初始值,使用最小二乘法得到参数估计的修正量,通过迭代方法得到参数估计的最终值,在计算量不大、原理简单的情况下实现了参数的精确估计。数字仿真数据的分析证明了本文提出的混合估计方法的有效性和准确性,本方法不局限于单一杂波模型的参数估计,具有很好的通用性。
[1] 司文涛,童宁宁,王强.海杂波背景中小目标检测算法研究[J].信号处理,2014,30(1):106-111.
[2] 马国哲,任丽莉,曹旭东.复杂波形体制下雷达导引头地杂波分析[J].航空兵器,2011(1):38-42.[3] 斯科尔尼克.M.I.雷达手册[M].北京:国防工业出版社,1978.
[4] 石志广,周剑雄,付强.K分布海杂波参数估计方法研究[J].信号处理,2007,23(3):420-424.
[5] 徐伟,陈永森.一种K分布杂波参数估计方法[J].舰船电子对抗,2013,36(3):82-84.
[6] 苏昭斌,陈红卫.海杂波复合K分布模型的参数估计[J].计算机应用与软件,2014,31(8):273-275.
[7] 任双桥,刘永祥,黎湘,等.广义K分布杂波模型参数估计[J].电子学报,2006,34(12):2278-2281.
[8] 朱人杰,陈红卫.基于遗传算法的海杂波K分布参数估计[J].舰船科学技术,2014(10):115-118.
[9] 刘川何.求解分裂可行问题的一种松弛投影算法[J].重庆工商大学学报(自然科学版),2016,33(1):16-18.
[10]余慧,王岩飞,闫鸿慧.一种K分布杂波参数估计的快速算法[J].电子与信息学报,2009,31(1):139-142.
[11]鉴福升,曾浩.实测海杂波数据的统计拟合优度分析[J].雷达科学与技术,2013,11(3):276-280.
(责任编辑 杨继森)
A Hybrid-Estimation Method of Clutter Distribution Models Based on MOM and Least Square Method
WU Yuan-wei1, JING Fu-gui1,2, WANG Li-bo1
(1. China Airborne Missile Academy, Luoyang 471009, China;2.Aviation Key Laboratory of Science and Technology on Airborne Guided Weapons, Luoyang 471009, China)
The traditional parameter estimation methods of clutter distribution models can’t balance the calculation efficiency and accuracy. To solve this problem, a generalized hybrid-estimation method based on MOM(method of moments)and least square method is presented. MOM is utilized to obtain the initial values of model parameters, which are iteratively optimized with least square method. The simulation results confirm the validity and accuracy of the method. The hybrid method realizes the accurate estimation of clutter parameters with little computational cost, and is not confined to the parameter estimation of any particular clutter model. It can be generally used in engineering application.
clutter distribution models; parameter estimation; MOM; least square method; hybrid-estimation
2017-02-11;
2017-03-10
交叉眼干扰与抗干扰技术研究基金资助项目(2014C01407R)
吴元伟(1989—),男,硕士研究生,助理工程师,主要从事雷达目标与环境特性研究。
10.11809/scbgxb2017.06.021
format:WU Yuan-wei,JING Fu-gui,WANG Li-bo.A Hybrid-Estimation Method of Clutter Distribution Models Based on MOM and Least Square Method[J].Journal of Ordnance Equipment Engineering,2017(6):95-98.
TN957;TJ765
A
2096-2304(2017)06-0095-04
本文引用格式:吴元伟,经富贵,王李波.基于矩估计/最小二乘法的杂波模型参数估计方法[J].兵器装备工程学报,2017(6):95-98.
