直升机旋翼翼型的非定常气动特性计算方法与验证研究
2017-07-02孟微胡和平周云
孟微,胡和平,周云
中国直升机设计研究所 直升机旋翼动力学重点实验室,江西 景德镇 333001
直升机旋翼技术是直升机设计的关键,其振动载荷的准确分析对旋翼动力学设计与直升机减振有着至关重要的作用。旋翼振动载荷预估技术包括非定常气动力建模、结构动力学建模和两者之间的耦合分析研究等,其中翼型的非定常气动特性建模是该技术的关键和难题之一。翼型非定常气动特性的准确分析,对提高旋翼振动载荷分析水平、提升直升机旋翼设计能力有极为重要的作用。
翼型来流在准定常状态下,随着迎角的增加会从附着流状态转为气流分离,在非定常状态下,随着迎角的增大则会产生动态失速。该现象是限制直升机飞行性能、引起直升机振动的因素之一,也是确定旋翼总升力、推力和使用限制的主要因素[1]。然而,准确预测动态失速现象对旋翼载荷和性能的影响是十分困难的,目前国内外对该现象的研究仍以基于试验的数值分析为主[2,3]。虽然用计算流体力学(CFD)模拟动态失速问题已取得了一定的突破,但因其对计算机的硬件要求高、计算量大、计算周期长等原因仍不适用于目前的工程计算。对于工程中旋翼的设计和分析来说,国际上通常采用与试验相结合的半经验模型,该类方法的优点是计算效率高且准确性好[3,4]。
本文以Leishman-Beddoes动态失速模型为基础,进行适用于旋翼振动载荷分析的二维翼型非定常气动特性建模与验证研究。将原动态失速模型中的10个经验系数简化为4个,并分别通过翼型静态试验和动态试验数据获得非定常模型参数表。最后通过试验数据对本模型进行验证。通过与试验的相关性分析表明,本模型具有较高的计算精度,可最终应用于旋翼的振动载荷分析中。
1 翼型的非定常气动模型
本文二维翼型非定常气动模型以Leishman-Beddoes动态失速模型为基础对其进行了简化。本模型的最大特点在于适用于时域求解,对于整个非定常气动问题的物理表示更加完善,方法简单直观,相比于其他半经验模型涉及的经验系数较少(仅为4个)。整个模型系统中使用的18个非定常气动模型参数,均从翼型特性的静态、动态试验数据中获得。
翼型来流在准定常状态下,小迎角时为附着流状态,迎角的进一步增大则转为气流分离(随翼型厚度的增加分为薄翼型分离、前缘分离和后缘分离)状态;在非定常状态下,迎角在超过静失速迎角后会产生动态失速。本模型根据翼型来流的物理过程,基于翼型的准定常非线性建模进行非定常气动建模,包括翼型附着流、气流分离和动态失速三部分,即三个子模型的综合。对三个子模型附着流、气流分离和动态失速及模型间的综合与参数确定进行详细介绍。
1.1 附着流计算
在本子模型中,采用经典的指数响应计算方法进行求解,其指数函数分为随时间衰减的脉冲函数(非环量部分)和经过几个弦长时间历程后趋于稳态解的渐进函数(环量部分)两类。目前的激励为迎角和变距率两项,如果假设翼型系统是线性的,那么根据叠加原理,通过Duhamel积分就可以得到本激励下的气动力响应。
本模型中,法向力系数Cn为:
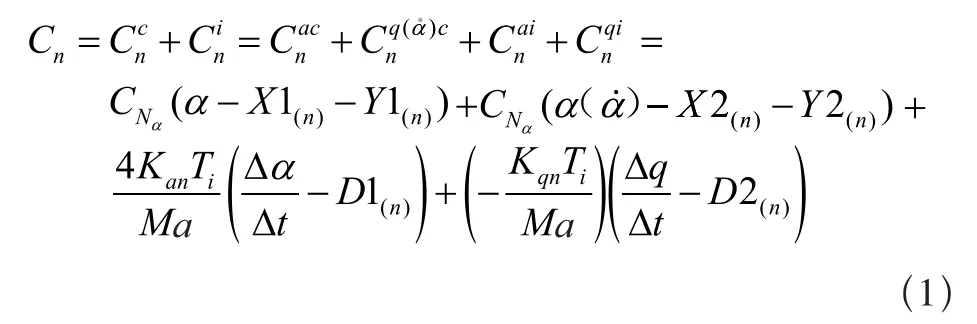
其中,各项递推公式为:
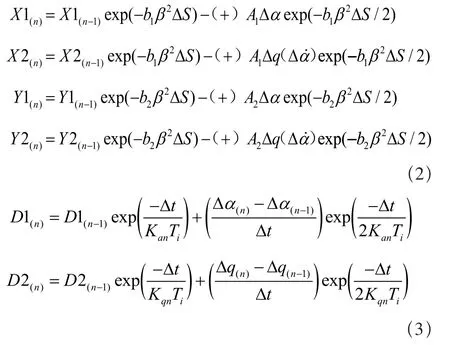
其中,CNα为法向力系数曲线斜率,c为弦长,a为声速,V为翼型剖面速度。力矩系数Cm为:
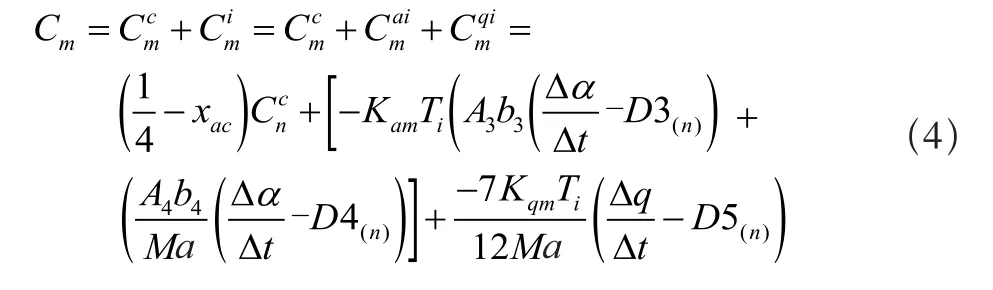
递推公式为:
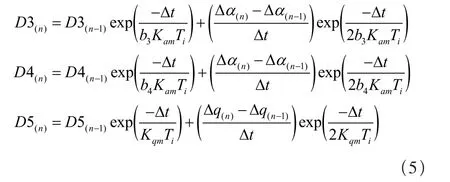
递推公式中变量为
模型简化:本模型中将以上模型计算所需的Kan、Kqn、Kam、Kqm统一简化为 Ki:
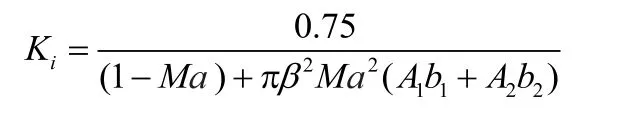
有 Kan=Ki,Kqn≈ Ki,法向力系数 Cn不变,力矩系数 Cm则转化为:
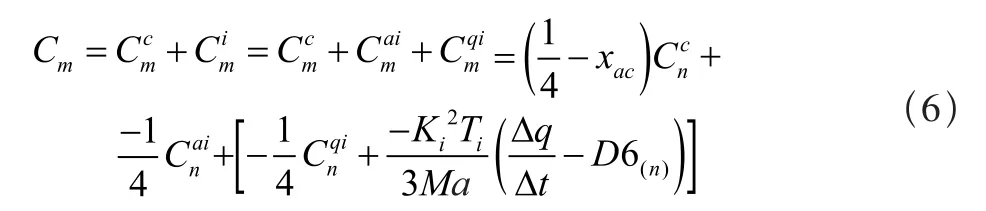
递推公式为:
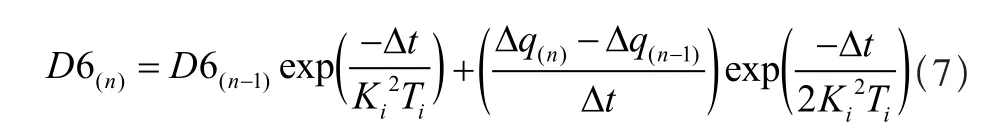
因此,本模型指数函数计算中所需的10个经验系数A1~A5,b1~b5简化为以下4个,取值为:A1=0.3,A2=0.7,b1=0.14,b2=0.53。
阻力系数Cd为:

式中:Cd0为零升阻力系数,弦向力系数Cc为:
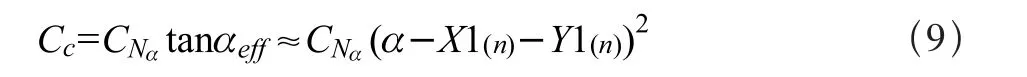
1.2 气流分离
尽管当翼型迎角随时间变化时,将临界前缘压力和压力梯度作为判断产生静态失速的准则不再适用,但是仍然可以通过与前缘压力直接相关的前缘气流分离的临界法向力系数CN1来判断翼型是否产生气流分离,该系数可由静态翼型试验得到。在非定常情况下,该模型对法向力系数做一阶滞后补偿处理,引入表明前缘分离的时间常数Tp,该参数是马赫数的函数,随翼型变化不大。分离点的确定则采用Kirchhoff-Helmholtz理论推导的后缘分离模型。该模型将翼型的法向力和迎角与后缘分离点联系起来,与翼型的静态升力失速特性试验结果相结合,从而确定等效分离点f(相对于弦长无量纲化)的变化,引入判断后缘分离的时间常数Tf。
本模型中,前缘分离修正的法向力系数为:
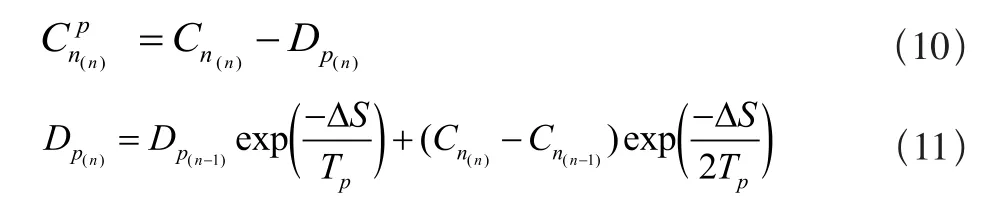
非定常情况下出现前缘气流分离的条件是Cnp> CN1,而后缘分离的法向力系数Cnf可近似为:
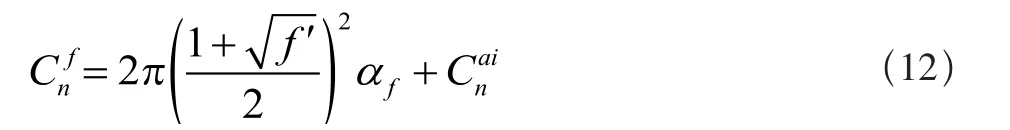
其中:
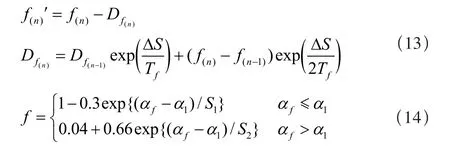
系数S1和S2定义了翼型的静态失速特性,有效迎角α1=Cn′/CNα,α1为分离点 f=0.7 时的迎角,f随迎角及 S1、S2和α1随马赫数的变化关系都可以通过静态升力数据得到。
力矩系数Cnf为:
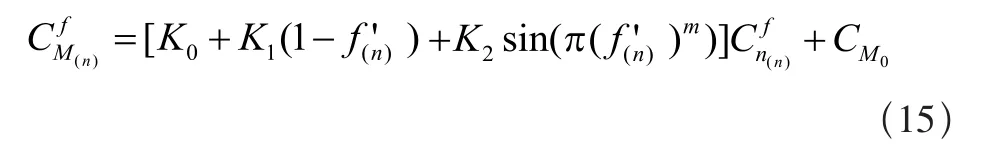
式中:K0、K1、K2都可以通过静态升力数据Cm/Cn曲线拟合得到。m对于NACA0012翼型取值为2,对于其他翼型,可以根据翼型数据选择0.5或1。
弦向力系数Ccf为:

式中:η为根据翼型系数引入的恢复因子,一般η=0.95,对于无黏流η=1。
1.3 动态失速
在非定常状态下,翼型来流随迎角的增大会产生动态失速现象。动态失速最大的特点为气流在翼型前缘产生集中涡并向后缘迁移至完全脱离后流入尾流中。虽然集中涡停留在翼型上时升力有一定的增加,但该集中涡极不稳定,很快脱离翼型使压心迅速后移,产生非常大的低头力矩,并增加了桨叶的扭转载荷,为其影响分析带来困扰。
本子模型采用公式模拟动态失速的物理过程,即涡在前缘的积累、形成集中涡、向后缘迁移和脱离翼型的整个过程。引入了涡衰减的时间常数Tv和涡沿弦长传播的时间常数Tvl,当生成涡的时间参数τv=0时分离点产生,τv=Tvl时涡到达后缘。Tv和Tvl在较大的马赫数范围内变化不大,且一般认为翼型对两者的影响不大。
在动态失速模型中,法向力系数为:
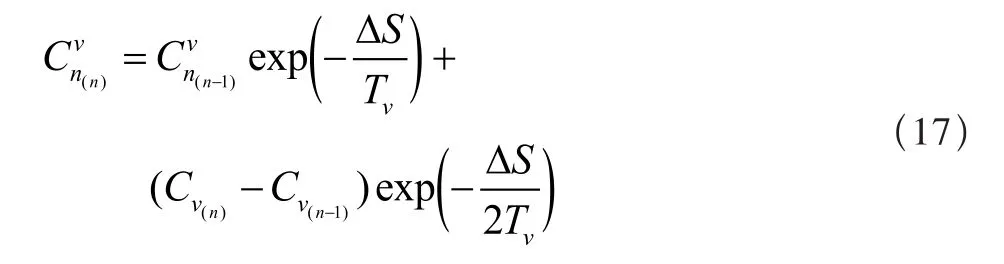
其中,动态失速集中涡产生的升力Cv为:
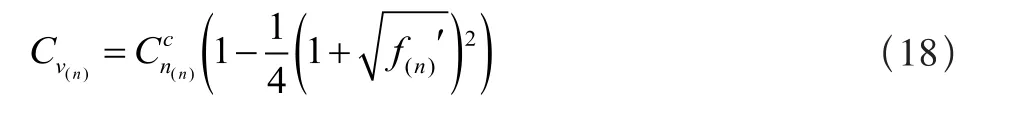
力矩系数Cmv为:
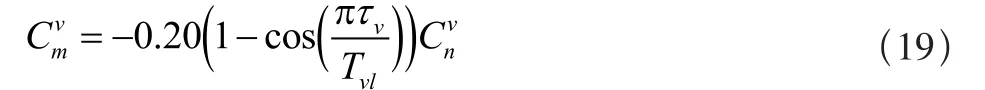
1.4 模型的综合
对以上三个子模型中各项系数进行综合,本方法的最终结果为:
(1)总法向力系数:

(2)总力矩系数:

(3)总弦向力系数:
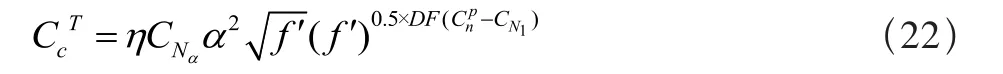
式中:DF为弦向力修正系数。
(4)总阻力系数:
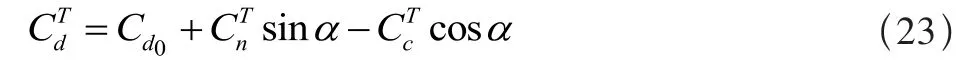
(5)总升力系数:

通过以上分析,可以看出三个子模型间互相耦合。附着流模型的输出结果作为气流分离模型的输入,而气流分离模型的输出结果作为动态失速(集中涡流出)模型的输入。附着流模型可以独立求解,但气流分离与动态失速模型之间因气流是否附着、集中涡是否脱离而产生的相互影响则要通过对时间常数的修正加以体现。为了扩大对于其他翼型的适用性,一般这种时间常数的修正仅限于Tf和Tv两个量值。为确保气流分离模型与动态失速模型中使用的时间常数准确,在每一次迭代步中时间常数都要重新修正。本模型的流程图如图1所示。
1.5 模型参数的确定
本模型中使用的4个经验系数在前面已经介绍。以下18个非定常气动模型参数根据翼型试验数据获得(见表1)。其中,前1~14项通过静态试验数据(翼型C81表)获得,后4个(15~18)表示动态失速特征的时间常数项通过动态试验数据获得,这4个时间常数项随马赫数变化较大,但随翼型的变化较小,本模型中在NACA0012翼型的时间常数项的基础上,根据本文中选取翼型的动态试验结果做微小修正后确定。
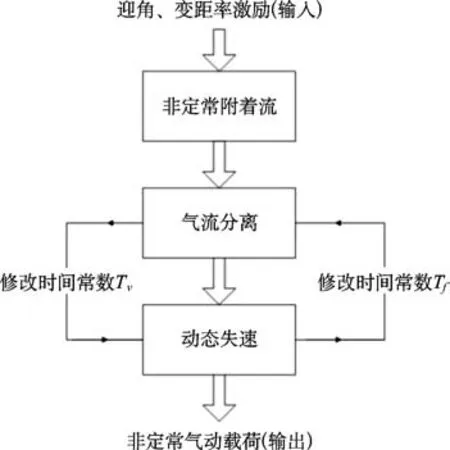
图1 非定常气动模型流程图Fig.1 Unsteady aerodynamic model fl ow
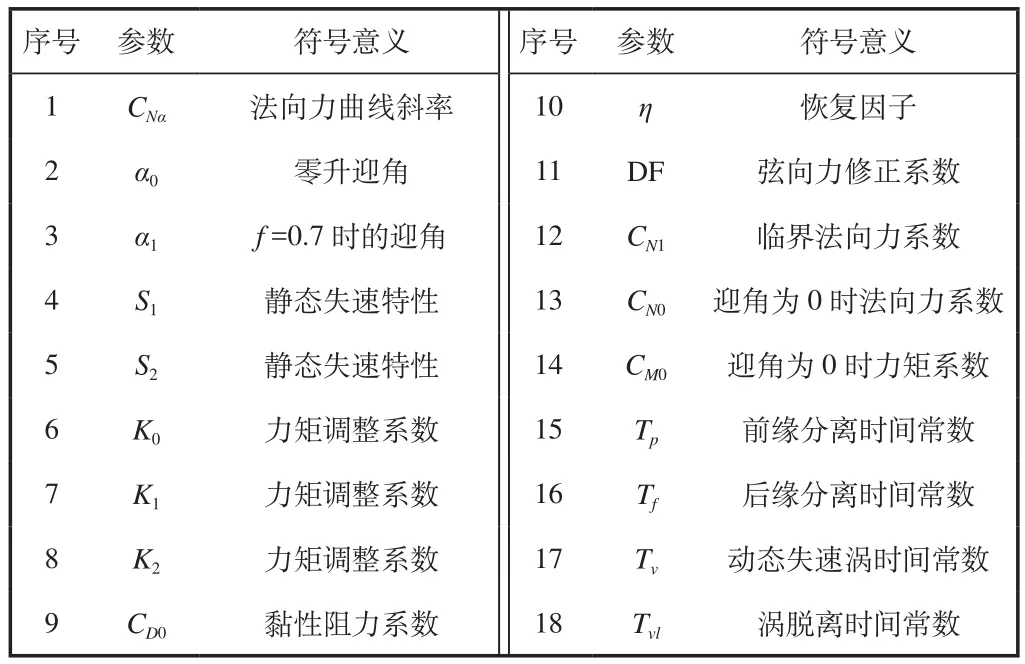
表1 非定常模型参数Table 1 The unsteady model parameters
2 计算验证
本文中的试验数据采用2011年俄罗斯中央空气流体动力学研究院(TsAGI)在TsAGI SVS-2风洞中进行的翼型动态失速特性试验数据,该翼型弦长为0.18m。在模型的验证中,分别进行Ma=0.3和Ma=0.6两个不同马赫数状态的计算与试验结果对比分析,验证本文的翼型非定常气动模型具有较好的计算精度和可靠性。
2.1 马赫数Ma=0.3
迎角α随时间t的变化分为三段。第一段迎角范围0°~6.9°,对应图中试验1和计算1;第二段迎角范围6.5°~14.6°,对应图中试验2和计算2;第三段迎角范围11.7°~22°,对应图中试验3和计算3。本状态马赫数Ma=0.3,折合频率k为0.029。如图2~图4所示。
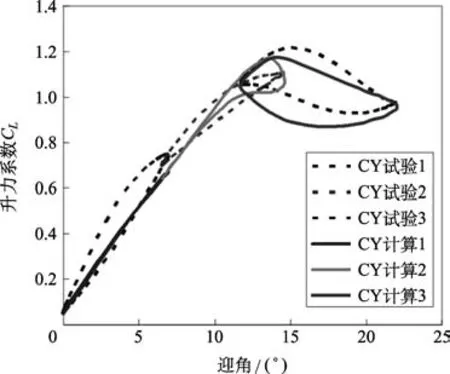
图2 升力系数随迎角变化(Ma=0.3)Fig.2 The lift coeff i cient varies with the attack angle(Ma=0.3)

图3 阻力系数随迎角变化(Ma=0.3)Fig.3 The drag coeff i cient varies with the attack angle(Ma=0.3)
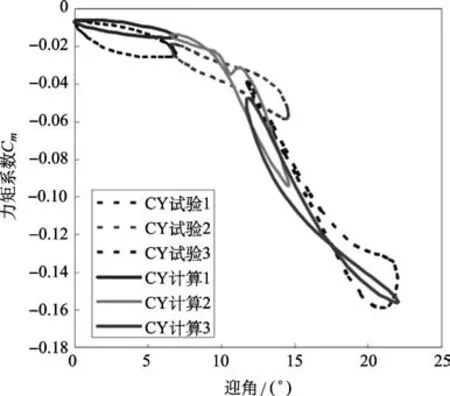
图4 力矩系数随迎角变化(Ma=0.3)Fig.4The torque coefficient varies with the attack angle(Ma=0.3)
从图中可以看出,在该状态下计算结果与试验数据符合地较为理想。升力系数的动态失速现象得以较好地捕捉;阻力系数反映出动态失速时阻力“8”字环的变化;力矩系数与试验结果符合的非常理想。总体来看,计算结果较为理想,且可以从试验数据判断出在该状态下动态失速迎角在12°附近,与计算结果基本一致。
2.2 马赫数Ma=0.6
迎角α随时间t的变化分为三段。第一段迎角范围0°~6.6°,对应图中试验1和计算1;第二段迎角范围7.4°~15.7°,对应图中试验2和计算2;第三段迎角范围13.9°~23.8°,对应图中试验3和计算3。本状态马赫数Ma=0.6,折合频率k为0.0146。如图5~图7所示。
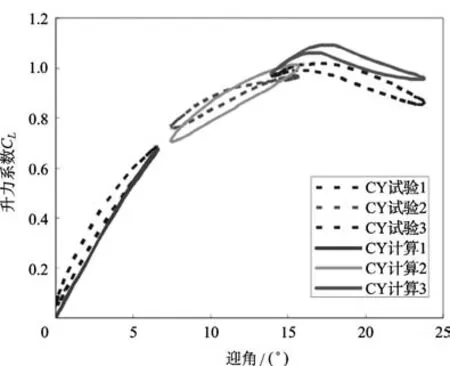
图5 升力系数随迎角变化(Ma=0.6)Fig.5 The lift coeff i cient varies with the attack angle(Ma=0.6)
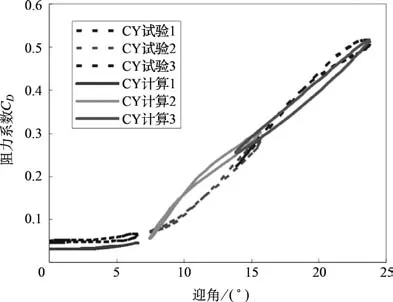
图6 阻力系数随迎角变化(Ma=0.6)Fig.6 The drag coeff i cient varies with the attack angle(Ma=0.6)
在Ma=0.6的状态下,整体来看计算结果与试验数据吻合地较好。动态失速产生的迟滞环小于计算结果,是由于折合频率较小造成的。升力系数最大值计算结果略大于试验结果,初步判断为涡的耗散时间常数Tv过小造成的;力矩系数偏差略大,可能是由于计算结果的动态失速迎角小于试验结果。根据试验和计算结果可以判断本计算中的翼型在该马赫数下的动态失速迎角为10°。
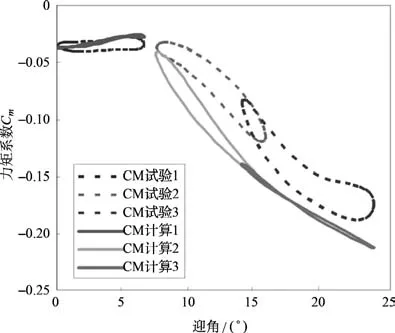
图7 力矩系数随迎角变化(Ma=0.6)Fig.7The torque coefficient varies with the attack angle(Ma=0.6)
3 结论
本文对建立可适用于直升机旋翼的振动载荷分析的翼型非定常气动模型进行研究,通过模型对模拟物理过程的阐述、模型参数的确定及模型计算与试验结果的对比分析,最终得到的如下结论:
(1)本模型在保证一定的计算精度的前提下,将原有Leishman-Beddoes模型指数函数中的10个经验系数简化为4个,且较于其他模型物理过程表述清晰,方法简单直观。
(2)本模型可以捕捉升力、阻力、力矩系数因动态失速产生的迟滞环;且计算结果准确地反映了该翼型在Ma=0.3、Ma=0.6下的动态失速迎角分别为12°、10°。
(3)本模型在不同马赫数下的计算精度都较为良好,与试验结果在变化趋势上一致性高;模型的可靠性也较高,可在旋翼的振动载荷预估分析中进行应用。
[1] Leishman J G. Principles of helicopter aerodynamics[M]. Second Edition. Cambridge: Cambridge University Press, 2006.
[2] Brain C. Modeling dynamic stall of SC-1095 airfoil athigh Mach Numbers[D]. Georgia Institute of Technology in Partial Fulfillment of the Requirements for the Degree Master of Science in the School of Aerospace Engineering, 2010.
[3] Ericsson L E, Reding J P. The difference between the effects of pitch and plunge on dynamic airfoll stall[C]// The 9thEuropean Rotorcraft Forum, 1983.
[4] Ashish B. Cobtributions to the mathematical modeling of rotor flow-fields using a pseudo-implicit free-wake analysis[D]. The University of Maryland in Partial of the Requirements for the Degree of Doctor of Philosophy, 1995.
