基于希尔伯特变换的直升机低频振动问题分析方法
2017-07-02王文涛查建平许宁
王文涛,查建平,许宁
中国直升机设计研究所,江西 景德镇 333001
随着社会的不断发展,军用/民用直升机的需求日益增加。使用环境及任务需求的多样化,使得直升机日益复杂化,机载任务设备更加多元化,大尺寸的外载外挂式设备(如桅杆式雷达、外挂吊舱等)也逐渐增多。目前,国内在装备的研制中更多地关注装备的整体性能、可靠性等,而对外挂设备外形导致的整机气动特性关注不足,可能产生额外的气动力作用到机体上;同时,由于分析和验证手段的局限性,当直升机上出现低频的振动问题时很难进行分析和处理。NH90、EH101、AH-64D“长弓阿帕奇”“科曼奇”等直升机在试飞初期均出现过“Tail shake/Buffet”等类似的低频振动现象[1,2],国内在直升机载荷测试、旋翼顶部加装大尺寸设备等项目的试飞中也多次出现过低频振动问题。
早期低频振动在对振动测试数据的常规分析中无法发现,仅靠飞行员的感受获知存在低频振动问题。飞行员的描述往往存在较大的主观性,其感受会受到个体敏感性、试飞科目、直升机状态等因素的影响产生较大的差异,同时飞行员在试飞时处于多振源的复杂振动和噪声环境中,因此仅靠飞行员描述对低频振动问题进行定位和分析无法给出解决问题的有效措施。
飞行振动测试是分析直升机振动的有效手段,直升机的振动特性[3,4]决定了振动测试数据中包含了主旋翼1Ω、kΩ(k为桨叶片数)等周期激励成分以及复杂的随机成分,数据分析发现这些成分对应低频振动的幅值相对较小,且没有明显的规律性,目前国内在直升机试飞中还没有有效的手段分析该问题。以傅里叶变换为代表的谱分析方法以周期信号为分析对象,而对非平稳信号将失去原有的意义,而希尔伯特变换(HT)是处理非平稳信号的有效方法,可用于对调制信号的解调[5],其衍生方法被广泛应用到小突变信号检测[6]、旋转机械信号分析[7]、轴承、齿轮等旋转部件的故障诊断[8,9]等。
本文通过对直升机中的低频振动现象及机理分析,基于希尔伯特变换,形成了直升机低频振动现象的分析方法,建立了飞行员描述与振动数据之间的对应关系,为低频振动问题的分析和处理提供了有效的客观评价手段。本文建立的方法已成功用于多个直升机型号的低频振动问题分析,取得了很好的效果。
1 现象及机理
直升机的振源一般包含主旋翼、尾桨、发动机及传动系统等旋转部件引起的周期激励和气动环境中的随机激励。对飞行员及乘员而言,主旋翼转速频率1Ω、一阶通过频率kΩ(k为桨叶片数)及其倍频NkΩ为其所感受到的主要振动源。
直升机的低频振动不同于上述常规的振动源,表现为“抖动”“晃动”“筛动”等现象,类似于坐船或骑马等,方向多为横侧向或垂向,有能量逐步积累然后释放的过程,无明显的规律性,时间间隔为1~5s。低频振动一般出现在某个或某些飞行状态或飞行姿态,与一个或多个因素相关联。因低频振动是无规律性的,“低频”仅指单位时间内发生的次数较少。
参考文献[9]指出直升机存在一种特殊的振动问题,其来源于主桨毂等区域的脱落涡对尾部结构的气动影响,如图1所示。影响因素有主桨毂、发动机进气及排气、整流罩等位置的气动外形以及旋翼到机身的距离等,表现为机体侧向一阶弯曲模态下的响应。而机体侧向一阶弯曲模态频率一般大于5Hz,这时需要与时间间隔1~5s建立关联,为分析低频振动问题的机理,引入经典的“拍现象”[10]。两个频率相近、幅值相同的简谐振动用式(1)来描述:

其中:a、ω和φ分别为简谐振动的幅值、频率和相位,其合成振动可以写成调制波形的形式:
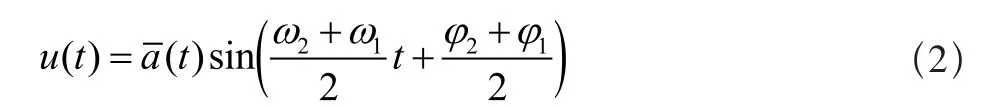
其中:
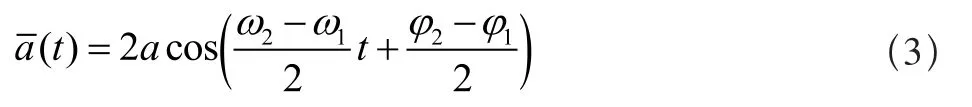
即合成振动是频率为(ω2+ω1)/2的变幅振动,其幅值为以频率(ω2-ω1)/2变化,是典型的幅值调制过程,实际呈现出的是幅值调制函数(t)的特性,即幅值包络线,如图2所示。
考虑任意非周期函数a(t)对频率为ω0的简谐振动调制的情况,即:

可描述典型的低频振动现象,其中被调制信号sin(ω0+φ)的频率ω0为机体侧向和垂向一阶弯曲固有频率。
因此,直升机中的低频振动为非周期调制函数对周期振动的调制,周期振动的频率为机体低阶固有频率,飞行员所感受的为非周期调制函数的变化规律,即周期函数的幅值包络。低频指单位时间内超出某一阈值的次数相对较少,时间间隔相对较长,如图3中出现幅值超出0.1g的时间间隔为2~3s。
图1 脱落涡对尾部干扰示意Fig.1 Turbulent wake effects on tail
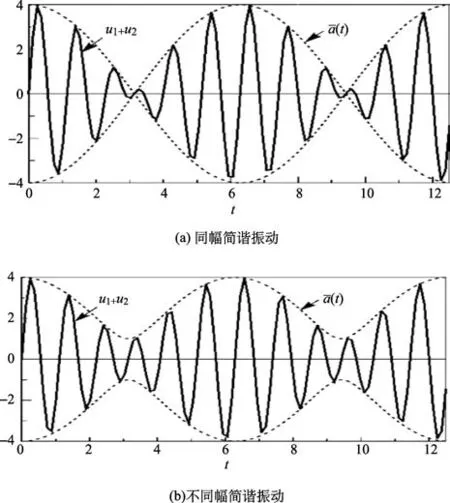
图2 两个同幅简谐振动合成的拍Fig.2 Beats with two simple harmonic vibrations
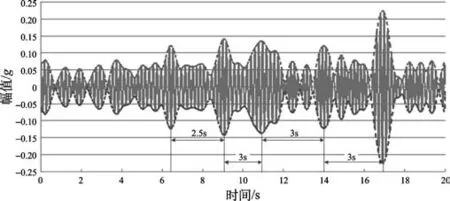
图3 典型低频振动信号Fig.3 Typical low frequency vibration signal
2 分析方法
2.1 希尔伯特变换
设实函数 x(t),t(-∞,∞),其希尔伯特变换[11,12]为函数x(t)与 1/πt的卷积,即:
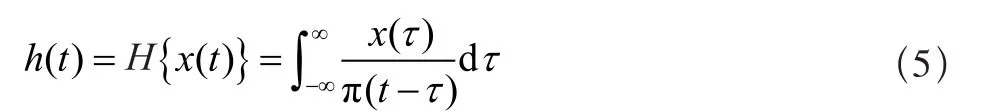
由傅里叶变换的性质可知,函数h(t)的傅里叶变换为函数x(t)的傅里叶变换X( f )与1/πt的傅里叶变换F(1/πt)的乘积,即:
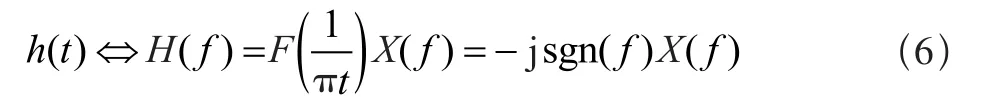
其中
引入解析函数:

即:

式中:A(t)为希尔伯特变换的包络
φ(t)为瞬时相位瞬时频率定义为
考虑式(4)所示的调制波形函数,根据希尔伯特变换的性质有:
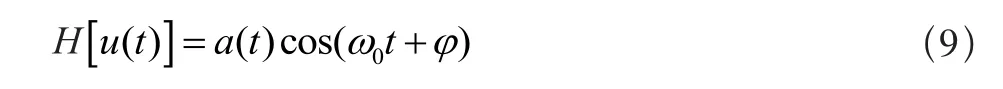
解析函数:

其包络为:
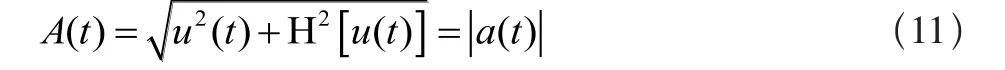
因此,通过希尔伯特变换,可以得到低频振动的幅值包络。
2.2 参数ü幅值图
直升机低频振动现象由飞行员提出,一般为直升机在某个特定的飞行状态或飞行姿态下出现,如某个速度下平飞、某个姿态爬升等,其感受为主观的,随飞行员的状态、关注点不同而有所差异。
为相对客观地反映低频振动与飞行状态、直升机姿态等参数的关系,建立参数p与振动幅值A之间的关系,形成参数ü幅值(püA)图,其中参数p可以为飞行状态参数如速度、压力高度、升降率等,可以为俯仰角、滚转角、侧滑角等直升机姿态参数,亦可为总距、周期变距等操纵量,同时根据需要可以为几个量的组合;振动幅值A为利用希尔伯特变换得到的幅值包络。通过püA图能够直观地看出振动幅值A随参数p的变化关系。
3 实例验证
为证明本文方法的适用性和有效性,应用本文方法对某型机试飞中的横侧向抖动问题进行分析。某型机调整试飞过程中,机组人员反映在速度170~220km/h平飞状态下机体存在较为明显的抖动现象,方向为横侧向,在1~2s出现一次,并存在类似能量累积然后释放的过程。利用本文方法分析,确定该低频振动现象为桨毂整流罩后部无规律的脱落涡引起了机体侧向一阶弯曲模态下的响应,是无规律激励对周期振动的调制,典型时间段低频振动数据如图4所示,利用希尔伯特变换获得振动幅值的包络如图5所示。对桨毂整流罩进行优化设计后,该低频振动现象得到明显改善。
利用本文方法对整个架次数据进行处理,以飞行速度作为参数p,得到速度与振动幅值(püA)的关系图,如图6所示。图中显示在速度170~220km/h状态,振动峰值的分布明显大于其他速度状态,与飞行员反映的规律一致。更改后的püA的关系如图7所示,图中显示在速度170~220 km/h状态,振动幅值明显小于初始状态,与飞行员所述“低频振动现象明显改善”相吻合。
由此可以证明,基于希尔伯特变换得到振动幅值的包络,然后与参数p形成的püA图,能够直观地呈现飞行员所反映的低频振动现象。püA图建立了振动测试数据与飞行员主观感受的对应关系,能够客观地描述直升机的低频振动现象,可以作为分析、定位和解决低频振动问题的有效手段。
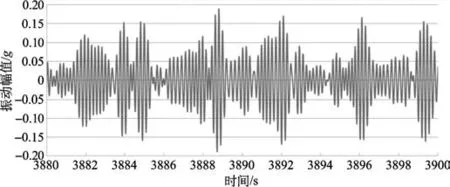
图4 低频振动信号Fig.4 Low frequency vibration signal
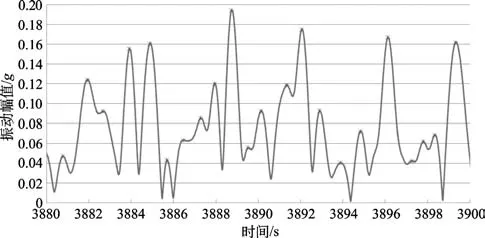
图5 低频振动的幅值包络Fig.5 Envelope of low frequency vibration signal
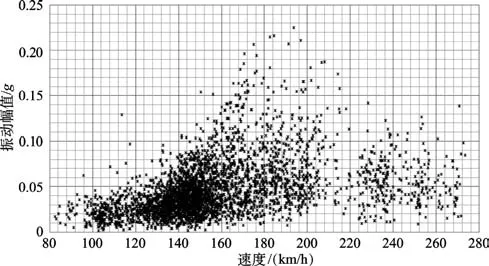
图6 初始状态püA关系图Fig.6 p-A relationship in initial status
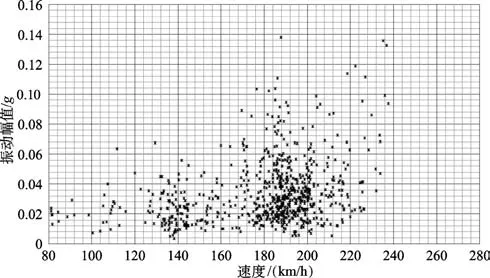
图7 更改状态püA关系图Fig.7 p-A relationship in improved status
4 结论
直升机中的“抖动”“晃动”“筛动”等低频振动现象为直升机低阶模态下响应的幅值包络。通过分析直升机低频振动的现象和机理,基于希尔伯特变换,引入püA图,形成了直升机低频振动现象的分析方法,相对客观地反映出机组人员的主观感受,为分析、定位和解决直升机的低频现象提供有效的手段。通过对某直升机横侧向抖动问题的分析,证明本文方法在分析直升机低频振动现象的适用性和有效性。
[1] Pieter D W, Michel T. Tail shake vibration in fl ight: objective comparison of aerodynamic configurations in a subjective environment[C]// AHS 52nd Annual Forum, Montreal, Quebec,1999: 2306-2316.
[2] Hassan A A, Thompson T, Duque E P, et al. Resolution of tail buffet phenomena for AH-64D Longbow Apache: a case study on the application of a modern CFD analysis tool for improved helicopter aerodynamic design[C]// AHS 53rd Annual Forum,Virginia Beach, Virginia, 1997: 1028-1048.
[3] 航空航天工业部科学技术研究院.直升机动力学手册[M].北京:航空工业出版社,1991.Science and Technology Institute in Ministry of Aerospace Industry. Handbook in helicopter dynamics[M]. Beijing:Aviation Industry Press, 1991.(in Chinese)
[4] 张晓谷.直升机动力学设计[M].北京:航空工业出版社,1995.ZHANG Xiaogu. Helicopter dynamics design [M]. Beijing:Aviation Industry Press, 1995.(in Chinese)
[5] 胡异丁,任伟新,杨栋,等.基于希尔伯特变换的非平稳调幅信号解调 [J].振动与冲击,2013,32(10):181-183.HU Yiding, REN Weixin, YANG Dong, et al. Demodulation of nonstationary amplitude modulated signal based on Hilbert transform [J]. Journal of Vibration and Shock, 2013, 32(10):181-183.(in Chinese)
[6] 王帮峰,林剑祥,芦吉云.基于EEMD-HT的飞行数据小突变信号检测 [J].振动、测试与诊断,2013,33(3):388-392.WANG Bangfeng, LIN Jianxiang, LU Jiyun. Detection of small mutation in fl ight data based on EEMD-HT [J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(3):388-392.(in Chinese)
[7] 胡劲松,杨世锡,吴昭同,等.基于EMD和HT的旋转机械振动信号时频分析[J].振动、测试与诊断,2004,24(2):106-110.HU Jingsong, YANG Shixi, WU Zhaotong, et al. Timefrequency analysis of vibration signal in rotating machinery[J].Journal of Vibration, Measurement & Diagnosis, 2004, 24(2):106-110.(in Chinese)
[8] 杨宇,于德介,程军圣.基于Hilbert边际谱的滚动轴承故障诊断方法 [J].振动与冲击,2005,24(1):70-72.YANG Yu, YU Dejie, CHENG Junsheng. Roller bearing fault diagnosis based on Hilbert marginal spectrum [J]. Journal of Vibration and Shock, 2005, 24(1):70-72.(in Chinese)
[9] 夏均忠,刘远宏,李树珉,等.应用Hilbert变换和ZFFT提取变速器齿轮故障特征[J].振动与冲击,2013,32(6):63-66.XIA Junzhong, LIU Yuanhong, LI Shumin, et al. Gearbox fault detection using Hilbert transform and ZFFT [J]. Journal of Vibration and Shock, 2013, 32(6): 63-66.(in Chinese)
[10] Bramwell A R, George D, David B. Bramwell’s helicopter dynamics[M]. Oxford: Butterworth-Heinemann, 2001.
[11] 胡海岩,孙久厚,陈怀海.机械振动与冲击[M].北京:航空工业出版社,1998.HU Haiyan, SUN Jiuhou, CHEN Huaihai. Mechanical vibration and shock[M]. Beijing: Aviation Industry Press, 1998.(in Chinese)
[12] Hahn S L. Hilbert transform in signal processing[M].Boston:Artech House, 1996.
