关于互感元件教学的三个问题
2017-07-01陈希有刘凤春李冠林
陈希有, 刘凤春, 齐 超, 李冠林
(1.大连理工大学 电气学院,辽宁 大连 116023;2.哈尔滨工业大学 电气学院, 黑龙江 哈尔滨 150001)
关于互感元件教学的三个问题
陈希有1, 刘凤春1, 齐 超2, 李冠林1
(1.大连理工大学 电气学院,辽宁 大连 116023;2.哈尔滨工业大学 电气学院, 黑龙江 哈尔滨 150001)
本文阐述了“电路”课程互感元件教学中的三个问题:消去互感前后磁链的变化;含有漏感和理想变压器的电路模型;工程上具有特殊工作条件的互感电路模型。在阐述这些问题时,运用了电磁学原理,衔接前后知识,联系工程案例,呼应后续课程。
互感;去耦;漏感;案例
0 引言
互感元件始终是电路理论教学中的重点和难点,这不仅是因为这种元件的理论作用,更是因为它与工程实际密切相关。在互感元件中,同时发生着电到磁和磁到电的双重转换,还涉及到电磁学的两大重要定律:安培环路定律和法拉第电磁感应定律。因此,对互感元件的教与学需要下大功夫。例如,文献[1]研究了全耦合互感并联,指出:当L1≠L2时,互感等效为短路;当L1=L2时,互感等效为L1;文献[2]用受控源转移法来消去互感,方法有趣且巧妙,等等。
本文阐述了笔者对互感元件的某些教学理解,深化了互感教学内容,联系了工程案例,做到了知识的前后贯通,并呼应了后续课程,可供因材施教时参考。
1 消去互感前后磁链变化对比
如何消去互感,使其成为简单的自感电路,是互感元器件教学的重要内容之一。但在消去互感的过程中,细心的学生会对磁链的变化产生疑惑。现举例如下。
利用消去互感原理,将图1(a)所示电路等效为图1(b)电路。图中La=M,Lb=L1-M,Lc=L2-M。再利用电感的并联、串联等效,又得到图1(c)。其中,
(1)

图1 互感的去耦等效
针对图1(a)—图1(c)三个电路,一些学生按下述方法分别计算三个电路各自的总磁链:
ψa=(L1i1+Mi2)+(L2i2+Mi1)
=(L1+M)i1+(L2+M)i2
(2)
ψb=La(i1+i2)+Lbi1+Lci2=L1i1+L2i2
(3)
(4)
学生通过计算发现,上述三个磁链彼此不相等,因此对消去互感的电路是否对磁链也等效产生疑惑。
初看起来,上述计算都有依据,即各个电感的磁链总和就是这部分电路的总磁链。但仔细分析发现,这种计算磁链的方法,不符合磁链的含义。对某线圈来说,磁链等于各线匝磁通的总和,磁通是闭合曲线围成区域的磁感应强度的通量,即面积分,如图2所示。所以,在计算总磁链时,要明确一个回路,不能不分青红皂白地把所有电感上的磁链加在一起。非同一回路内电感的磁链相加无意义。

图2 磁通的含义
对图1中的三个电路取相同回路,再把回路的总磁链进行比较,结果就相同了。例如:

(5)

(6)
图1(c):ψc=Leqi=ψa1=ψa2=ψb1=ψb1
(7)
然而,可以验证,图1中三个电路的磁场储能是一样的,并且可以用每个电感的能量之和作为总能量,这是符合能量守恒规律的。即,
=0.5Leqi2
(8)
上述回路总磁链与各电感磁链的关系,还可以用对偶的电容电路来理解,如图3所示。若计算电荷,需要指定节点,例如a点。简单地将三个电容上的电荷加在一起是没有意义的。

图3 与图1(b)对偶的电容电路
2 考虑漏感的互感元件等效电路
课堂上讲授互感去耦等效时,会出现负电感,负电感的物理意义难以解释,使得这种方法只具有计算意义。工程上往往更加关心耦合线圈的漏感,所以帮助学生建立含有漏感的互感电路模型,更加符合工程需要,也能与后续的电机与拖动课程相呼应。为说明这一过程,需要先建立全耦合互感的含理想变压器电路模型。
2.1 含理想变压器的全耦合互感元件的电路模型
初级线圈和次级线圈紧密并绕在一起时可以将其近似为全耦合。但为了便于标注,仍画成图4所示的分离形式,忽略漏磁通,就成为全耦合互感。它可以用图5所示的含理想变压器的电路模型来表示。模型中的变比n和励磁电感Lm与L1、L2的关系,可以基于端口方程一致的等效含义,在数学层面上进行分析。对此,一些教科书已有所阐述[3,4]。在此从略。但是,如果能借助物理现象得出n及Lm与L1、L2的关系,在教学上则能够更加突出物理概念。下面是这种方法的思路。
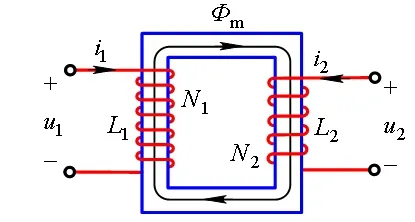
图4 全耦合互感

图5 全耦合互感的含理想变压器电路模型
在全耦合条件下,每匝线圈的磁通都相同,因此不难理解,端口电压之比(或电动势之比)等于匝数之比。同时,两个线圈的自感又分别正比于各自的匝数的平方(物理学中已有这样的结论),且比例系数相同。因此,理想变压器的变比可以用匝数和自感计算如下:
(9)
在图4的全耦合互感中,次级开路时,初级侧的等效电感就是初级的自感 。在图5的电路模型中,次级开路时,从初级侧得到的等效电感是Lm。因为两个电路等效,所以必然存在Lm=L1。在此关系下,当初级侧开路时,从图5的次级得到的等效电感为Lm/n2=L2,这正是图4的初级开路时,从次级得到的等效电感。由此验证了Lm=L1的正确性。
2.2 含漏感和理想变压器的互感元件的电路模型
非全耦合互感磁通分布如图6所示,分为三部分:单独与初级交链的磁通Φσ1,产生初级漏磁链;单独与次级交链的磁通Φσ2,产生次级漏磁链;同时与初级和次级交链的公共磁通即主磁通Φm,起到能量传递的作用。主磁通就是全耦合时所考虑的磁通,因此可以用全耦合互感表示主磁通与初级和次级的交链关系。然后在全耦合基础上,通过增添两个线圈,分别表示初级和次级的漏磁通,这样的模型就可以表示非全耦合互感,结果如图7所示。这完全是依照磁通的实际分布进行的,合情合理。

图6 非全耦合互感的磁通分布
设对应漏磁通的自感即漏感分别为Lσ1和Lσ2,则全耦合互感中的两个自感就变成了L1-Lσ1和L2-Lσ2,电路模型如图8所示[3]。

图7 用两个自感和全耦合互感表示非全耦合互感

图8 非全耦合互感的一种电路模型
(10)
上式符合k=1时无漏磁的结论。根据2.1节对全耦合互感的阐述,图8可以用图9所示的含理想变压器和漏感的电路模型来等效。根据全耦合互感的结论并考虑到式(10)的关系,图9中变比为
(11)
结果仍然是两个自感之比的平方根。

图9 非全耦合互感含漏感和理想变压器电路模型
图9中的各个元件对应的物理现象是明确的:Lσ1、Lσ2对应漏磁;理想变压器对应能量传递;Lm对应耦合电感建立的磁场。
实施上述教学须在学完理想变压器之后,再前瞻到互感元件,因而加强了前后内容的有机联系。

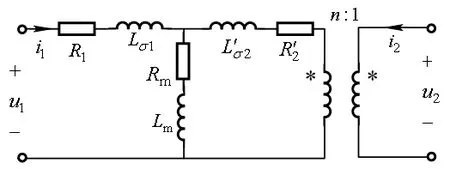
图10 变压器初级回路的T形等效电路
3 依赖于工作条件的互感电路-工程案例
工程上存在一些互感,它们有特殊的工作条件。针对这些特殊条件,可以建立相应的电路模型。下面举出两例,可用于案例教学。
3.1 四线圈共模变压器
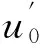

图11 电力传动中共模电压抑制电路
下面着重分析共模变压器部分。根据图11中的耦合方式,可以建立共模变压器的电压与电流相量关系。相对双线圈互感,共模变压器虽然相互耦合的线圈为四个,但独立的线圈电流仍然是两个,它们与线圈电压的关系如下:
(12)
根据这些关系可以得到图12所示的共模变压器电路模型。这样的教学,可以使学生初步了解建模过程,扩展学生对磁耦合器件的认识广度。图中出现的受控源,可以让学生理解受控源在电路建模中的作用,用它来表示不同端口电压与电流之间的依赖关系。
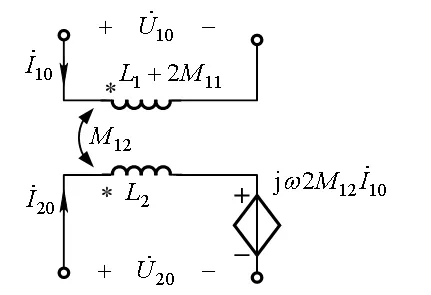
图12 含受控源的共模变压器电路模型
3.2 Z源逆变器中的互感
图13是可用于新能源发电和电力传动中的Z源逆变器简化电路。在电路设计中已保证L1=L2,并且i1=i2。由于这两个电感存在上述参数关系和电流关系,因此,可以把它们缠绕在同一个磁路上,构成耦合互感,如图14所示。对电压电流关系分析如下:

图13 新能源发电与电力传动中的Z源逆变器

图14 Z源逆变器中电感的实现
(陈希有等文)
(13)
因为图13和图14中的电压和电流不是正弦量,因此上面使用了微分方程。
4 结语
本文介绍了针对重要的互感元件知识点,需要深入挖潜教学内容、教学方法和工程案例,使学生能够从不同的角度,加深对互感元件的认识。深究概念、前后衔接、联系实际、联系后续课程,这些方法都可以起到很好的教学效果。
[1] 于歆杰,许军,朱桂萍.关于全耦合的一道习题的讨论[J]. 南京. 电气电子教学学报. 2012,34(3):1-3.
[2] 李盛才,李新. 消去互感的一种新方法[C]. 电工理论与新技术2004年学术研讨会论文集. 北京. P. 284-286.
[3] 李瀚荪. 简明电路分析基础(M). 高等教育出版社,北京。2002.7.
[4] 胡翔骏.电路分析(第2版)(M). 高等教育出版社,北京. 2001.6.
[5] 孙建忠,刘凤春. 电机与拖动(第2版)(M). 机械工业出版社. 北京. 2013.4.
Three Issues about the Mutual Inductor Teaching in Circuit Course
CHEN Xi-you, LIU Feng-chun, QI Chao,LI Guan-lin
(1.SchoolofElectricalEngineeringofDalianUniversityofTechnology,Dalian116023,China;2.SchoolofElectricalEngineeringofHarbinInstituteofTechnology,Harbin150001,China)
This paper described three issues in the Circuit course teaching: the variations of magnetic flux before and after mutual inductance eliminated; the circuit models of coupling inductor which contains the leakage inductance and ideal transformer; the circuit models of coupling inductor working at the special conditions. In the introduction of these issues, the principles of electromagnetism are used, pre order and subsequent knowledge is joined, the engineering cases are demonstrated, and the follow-up courses are echoed.
mutual inductor; decoupling; leakage flux; case
2016-05-17;
2016-06-12
陈希有(1962-),男,博士,教授,主要从事电能变换的教学与科研,E-mail:chenxy@dlut.edu.cn
TM13
A
1008-0686(2017)02-0099-05
