10 kV内胶装瓷柱式绝缘子优化选型

安 帅，吴 昊，柴 俊

(国网上海市电力公司市北供电公司，上海 200072)

10 kV内胶装瓷柱式绝缘子优化选型

安 帅，吴 昊，柴 俊

(国网上海市电力公司市北供电公司，上海 200072)

10 kV配电线路绝缘子是实现配电线路与地电位之间电压隔离的重要电力设备。研究了10 kV内胶装瓷柱式绝缘子的长度、表面伞裙形状、内电极和外电极等几个影响内胶装瓷柱式绝缘子电场强度分布的典型因素，得出以下结论：绝缘子伞群对绝缘子表面最大电场强度影响很小；绝缘子的长度影响绝缘子表面最大电场强度，绝缘子越长，其表面最大电场强度越小；绝缘子内电极球半径对绝缘子表面最大电场强度影响很小，而绝缘子内电极杆径越大，绝缘子表面最大电场强度越大。这些计算的结果可以为10 kV内胶装瓷柱式绝缘子的设计提供依据并且可以优化设计方案。

10 kV配电线路；瓷柱式绝缘子；电场强度

随着我国经济的日益发展，配电网日益复杂，配线电路中10 kV线路绝缘子使用量也越来越多。运行过程中，由于绝缘子两端承受了导线和大地之间的电压，绝缘子在不同部位会分布有电场强度[1-3]，电场强度最大的地方容易发生电晕并且引起绝缘子沿面闪络甚至引起绝缘子整体击穿，对配电线路的安全运行造成一定的影响。因此，在绝缘子承受电压不变的情况下，如何降低绝缘子表面最大电场强度成为一个迫在眉睫的问题[4-6]。本文主要以10 kV内胶装瓷式绝缘子(以下简称绝缘子)为例，从绝缘子结构入手，经过一些简化进行建模，然后利用有限元分析的方法对各个模型进行计算分析，寻求绝缘子的最佳外形。

1 模型的建立

有限元法是将需要计算的区域利用某种方法分割成为有限个小区域，这些小区域一般叫做“单元”，分割好小区域之后通过求解边界问题的原理将各个小区域进行计算，最后将各个小区域的结果进行总和得到整个求解区域的结果[7-9]。

本文主要利用Ansoft Maxwell仿真软件进行建模，在进行仿真前需对研究对象进行简化处理[10-11]。为了更加方便地利用Ansoft Maxwell进行电场计算提供条件，进行如下简化。

(1)以轴截面一半代替整个绝缘子。由于绝缘子是具有轴对称特征的三维体，故将模型简化为轴截面的一半并设置轴对称等条件建立模型。

(2)导线的空间影响忽略不计。导线与绝缘子贴合的部分对绝缘子电场强度影响大，而导线其他远离绝缘子的部分经计算验证对绝缘子表面电场强度影响不大，所以忽略。

(3)以有限边界代替无穷远边界。就是将无穷远处的边界，移位到靠近负荷绝缘子的一定距离位置。这样简单处理后，绝缘子附近的电场将有所增强，由于绝缘子的整体尺寸很小，距离其不远处的电场线就稀疏了，所以带来的误差不大。

本文只考虑影响绝缘子最大电场强度的因素[2-6]，因此主要考虑绝缘子的伞群形状及数量；绝缘子长度；绝缘子的电极布置型式及形状这3个因素。

根据这些简化，在Ansoft Maxwell中建立的一个绝缘子模型见图1。

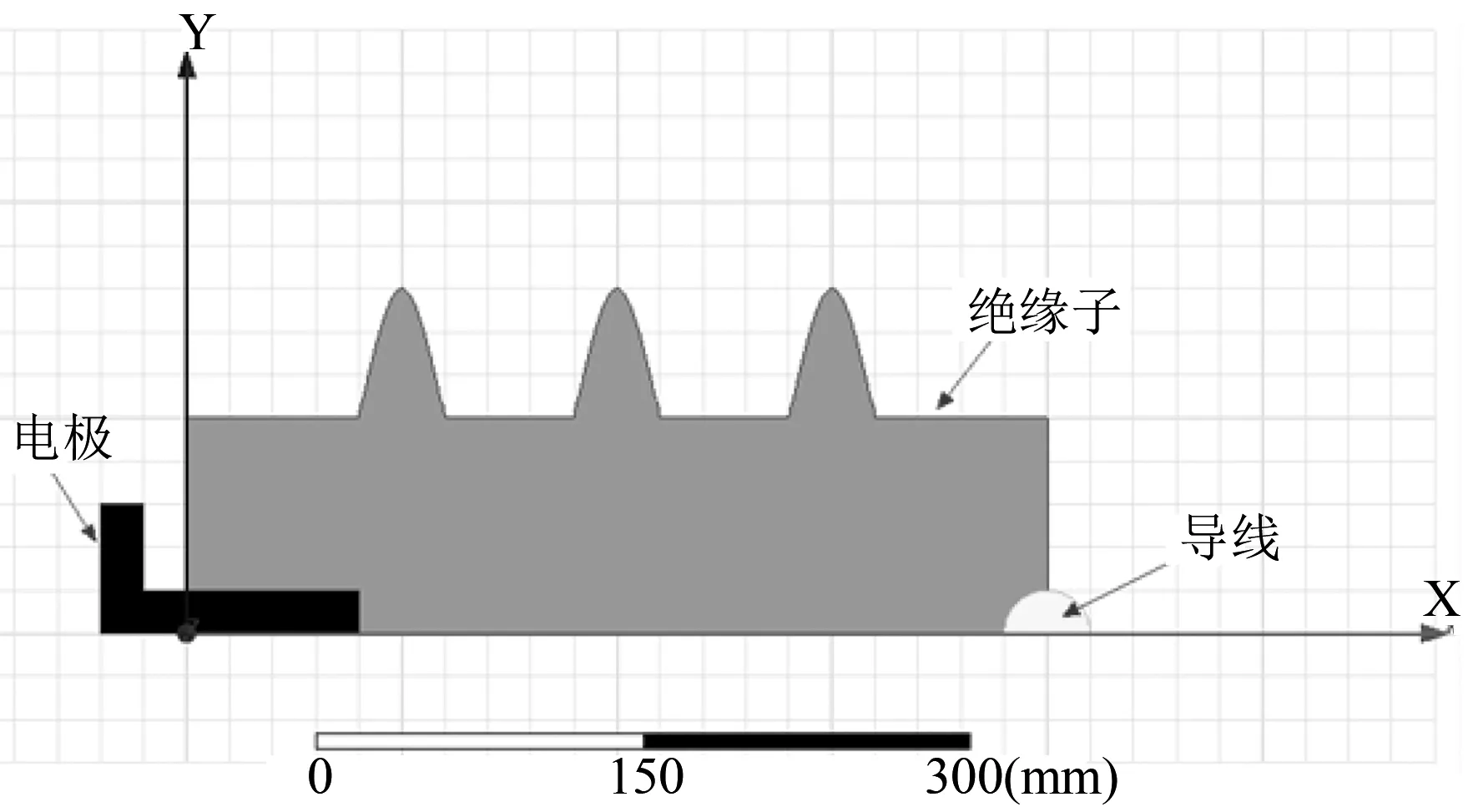
图1 绝缘子模型示意图

图1中，绝缘子长度为400 mm的绝缘子材料定义为glass,介电常数为5.5，导线材料定义为aluminum，电极材料定义为stainless steel。

在建立完模型后，对空气的外围定义气球边界条件，导线定义激励源为8.16 kV，电极定义为接地电压0 V。其中，所取激励源8.16 kV是指10 kV线电压转换为相电压的最大幅值[12-13]。

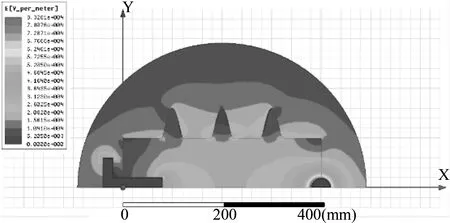
图2 绝缘子电场强度分布云图

对模型进行计算，整个绝缘子的电场强度的分布见图2，箭头所指之处电场强度越大。

绝缘子最大电场强度为0.83 kV/cm，整个绝缘子附近最大电场强度出现的位置见图3。

图3 绝缘子最大电场强度出现位置示意图

2 伞棱形状及数量的影响

根据提出的简化和假设，在Ansoft Maxwell中建立不同伞棱形状的绝缘子模型，见图4，其中绝缘子长度均为400 mm。

图4 不同伞群形状绝缘子模型示意

经过计算得到7个绝缘子模型表面最大电场强度见表1。

表1 伞棱形状不同的绝缘子模型最大电场强度

从表1可以看出，由于伞棱形状的改变，导致绝缘子表面电场强度发生了相应的变化：从1号至5号5个模型中可以看出，绝缘子伞棱形状会影响绝缘子最大电场强度，但是并无规律性；从1号、5号、6号模型的计算结果可以看出，绝缘子伞棱越多绝缘子最大电场强度越大，虽然绝缘子伞棱的增多会增大绝缘子的爬距，但是最大电场强度的增大不利于绝缘子抑制沿面放电，因此增加绝缘子伞棱数对防止绝缘子沿面放电不一定有益。总的来说，绝缘子伞棱对绝缘子最大电场强度有一定的影响，但影响不大，并且无规律性。从设计角度来看，从伞棱这一因素来有效降低绝缘子最大电场强度是比较困难的。图5为以上7个模型电场分布云图。

图5 不同伞群形状绝缘子电场分布云图对比示意

从图5可以看出，伞棱的大小、形状、数量等均会影响到绝缘子周围电场强度的均匀程度。经过对比可以得出：模型1附近的电场强度最均匀；从模型2和3的对比可以看出，伞棱越大电场强度越不均匀；从模型5和6可以看出，相同形状的伞棱越多电场强度与不均匀。伞棱的形状和长度决定了绝缘子的爬距，因此伞棱的存在是必然的，但是如何在保证爬距的情况下让绝缘子附近的电场强度保持均匀还有待进一步研究。

3 绝缘子长度的影响

在Ansoft Maxwell中建立不同长度的绝缘子模型，见图6。其中，4个模型具有相同的伞棱形状和数量。

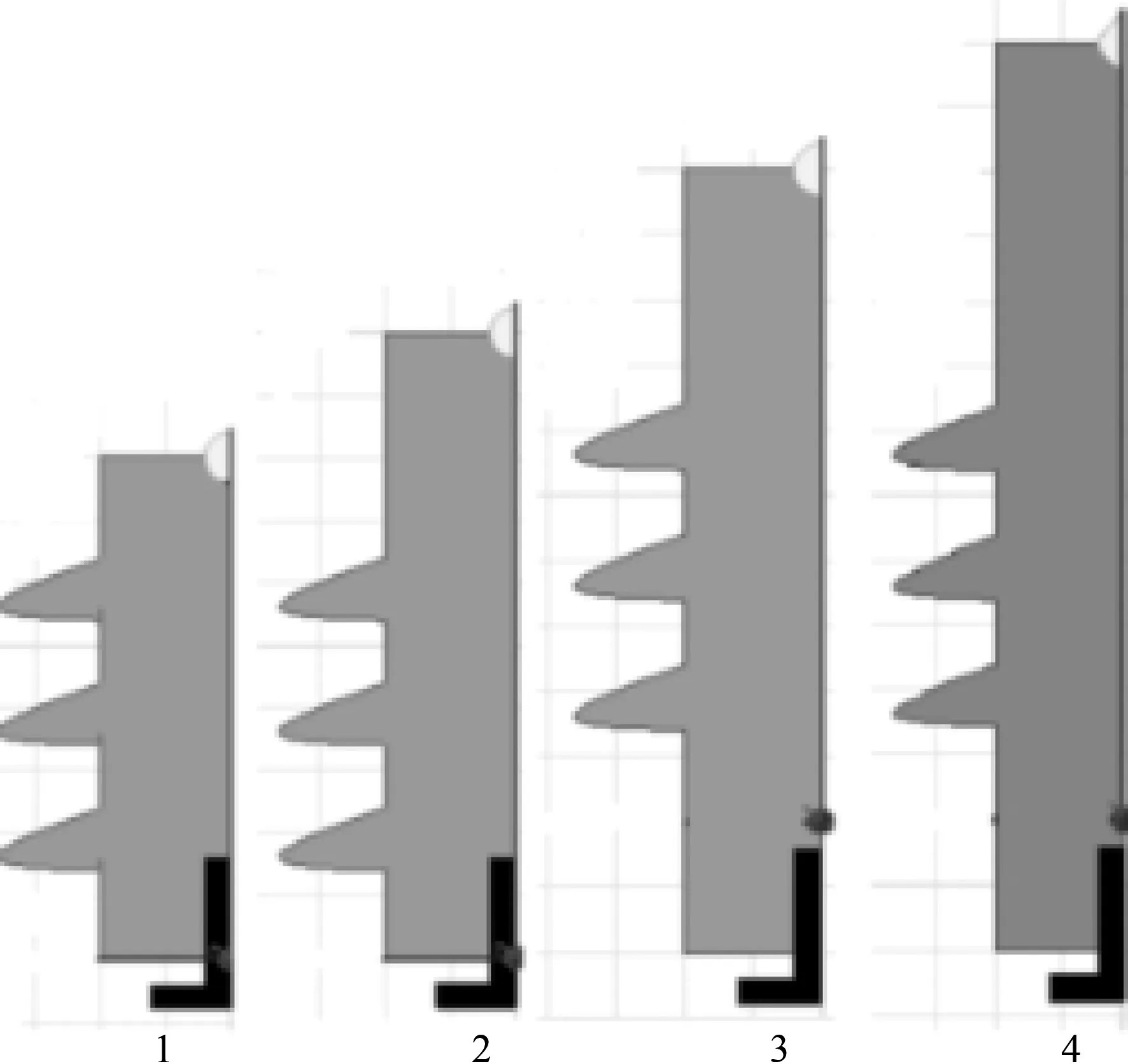
图6 不同长度绝缘子模型示意

对4个模型进行仿真计算，4个模型中有相同的伞棱，最终得出各自最大电场强度，见表2。

表2 长度不同的绝缘子模型最大电场强度

不同长度绝缘子最大电场强度分布见图7。

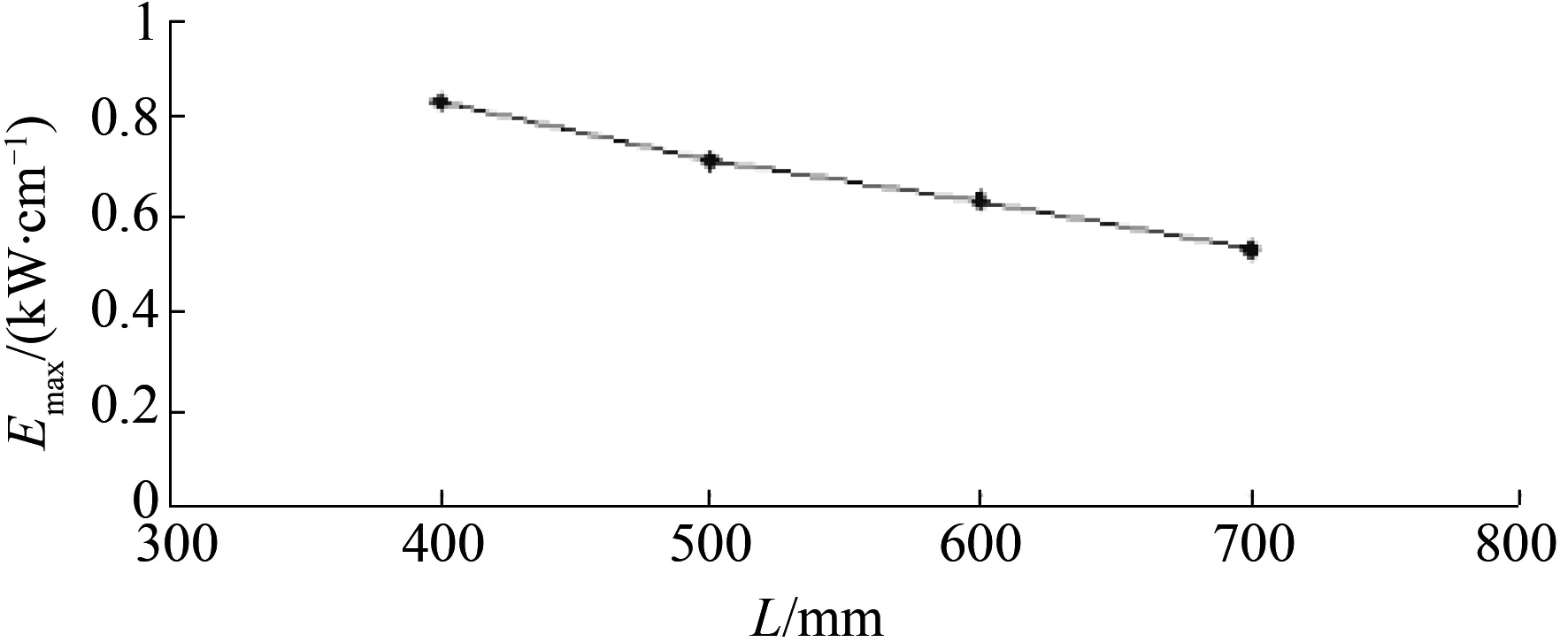
图7 不同长度绝缘子最大电场强度分布

不同长度绝缘子模型附近电场强度分布云图见图8。

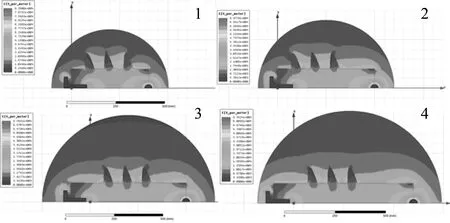
图8 不同长度绝缘子最大电场强度分布

从表2以及图8可以得出，绝缘子长度越长，绝缘子表面最大电场强度越小。从图8可以得出，伞棱相同的情况下，绝缘子越长，绝缘子附近的电场强度越均匀。

在研究的基础上，对不同长度无伞群的绝缘子进行计算，模型如图9所示。

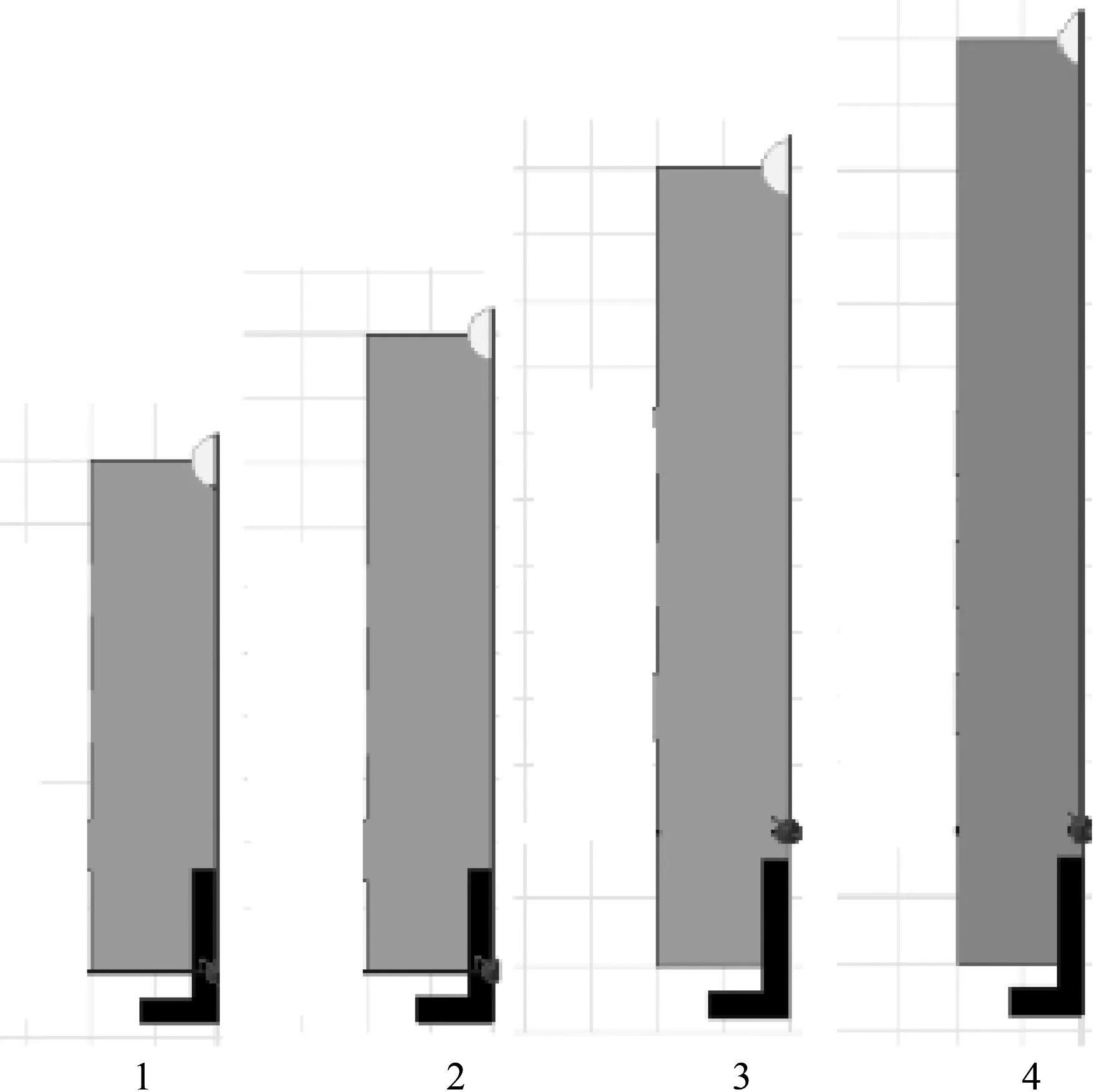
图9 无伞群不同长度的绝缘子模型示意图

经计算，4个绝缘子模型最大电场强度见表3。

表3 无伞群长度不同的绝缘子模型最大电场强度

这组绝缘子附近电场强度分布云图见图10。

图10 无伞群不同长度绝缘子模型场强分布云图

从图10可以看出，依然存在绝缘子越长其表面最大电场强度越小的情况。不同长度、没有伞棱情况下，绝缘子电场强度均匀程度相差不大，也就是说没有伞棱的情况下，绝缘子的长度对绝缘子附近平均电场强度影响不大。这2组模型中，绝缘子模型的长度是从400～700 mm。虽然600 mm及其以上的长度已经超出了10 kV绝缘子的最大长度，已经不具有实际意义了，但只是做可行性研究，仅验证结论的正确性。根据这个结论，如果条件允许，设计人员可以适当增加绝缘子长度，这样既能增加绝缘子爬距，又有效降了低绝缘子最大电场强度，达到了绝缘子优化的目的。

下面将相同长度的绝缘子有伞群和无伞群时，其表面最大电场强度进行了比较，比较结果见图11。

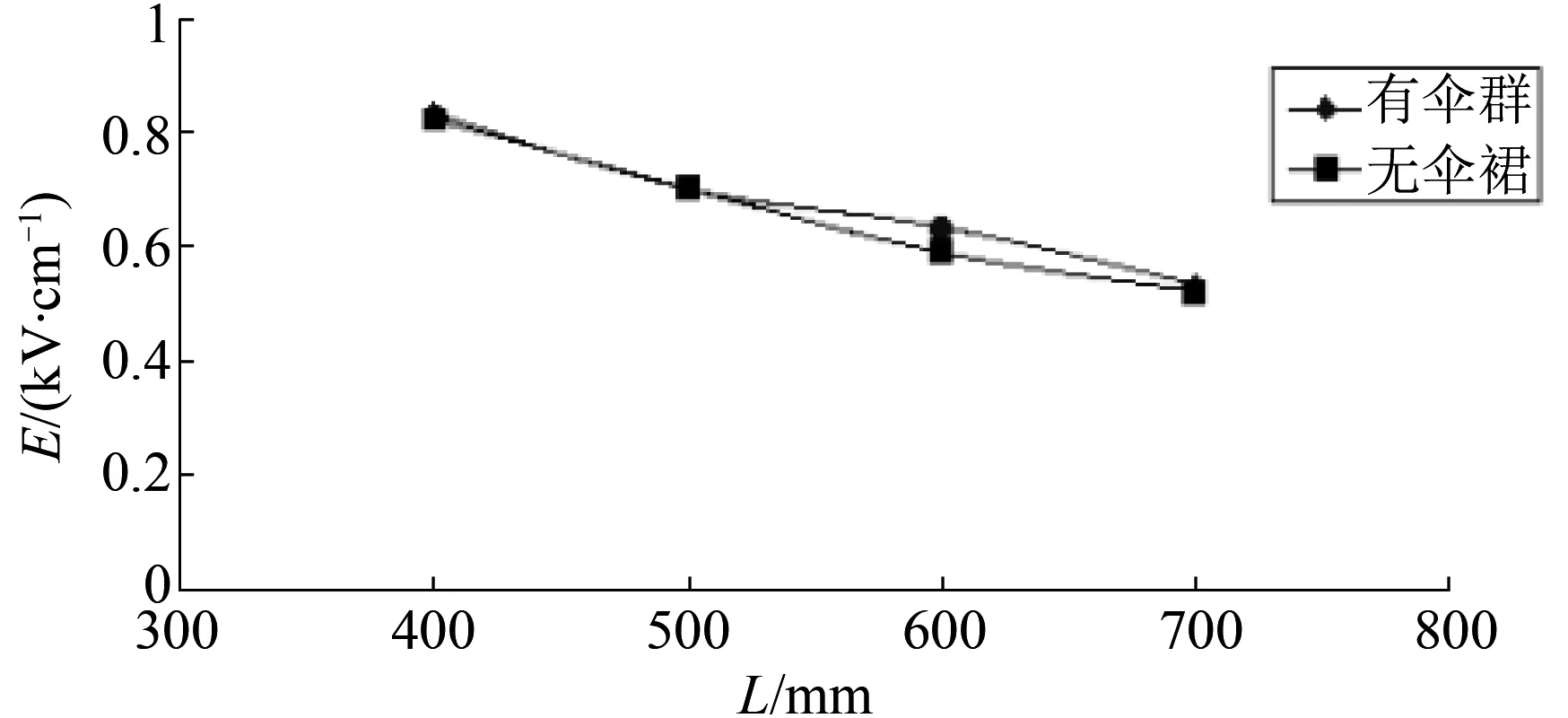
图11 相同长度有无伞群模型最大电场强度比较结果

从图11可以看出，两条曲线基本重合，也就是伞棱的有无对绝缘子最大电场强度影响不大，但有伞棱的情况下表面电场强度略大。如果设计绝缘子时要降低绝缘子的表面的最大电场强度，不应从伞棱角度出发。

4 绝缘子电极布置型式及形状的影响

下面主要研究绝缘子内电极对最大电场强度的影响。内电极从内电极球半径以及内电极杆径来考虑。

4.1 不同半径内电极球的影响

相同长度的绝缘子(400 mm)按照相同杆径(均为20 mm)，不同内电极球半径建立的绝缘子模型如图12所示。

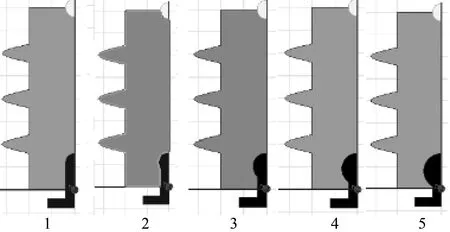
图12 内电极球半径不同的绝缘子模型示意图

内电极球半径不同的绝缘子模型最大电场强度，仿真结果见表4。不同半径内电极球最大电场强度分布见图13。

表4 内电极球半径不同的绝缘子模型最大电场强度

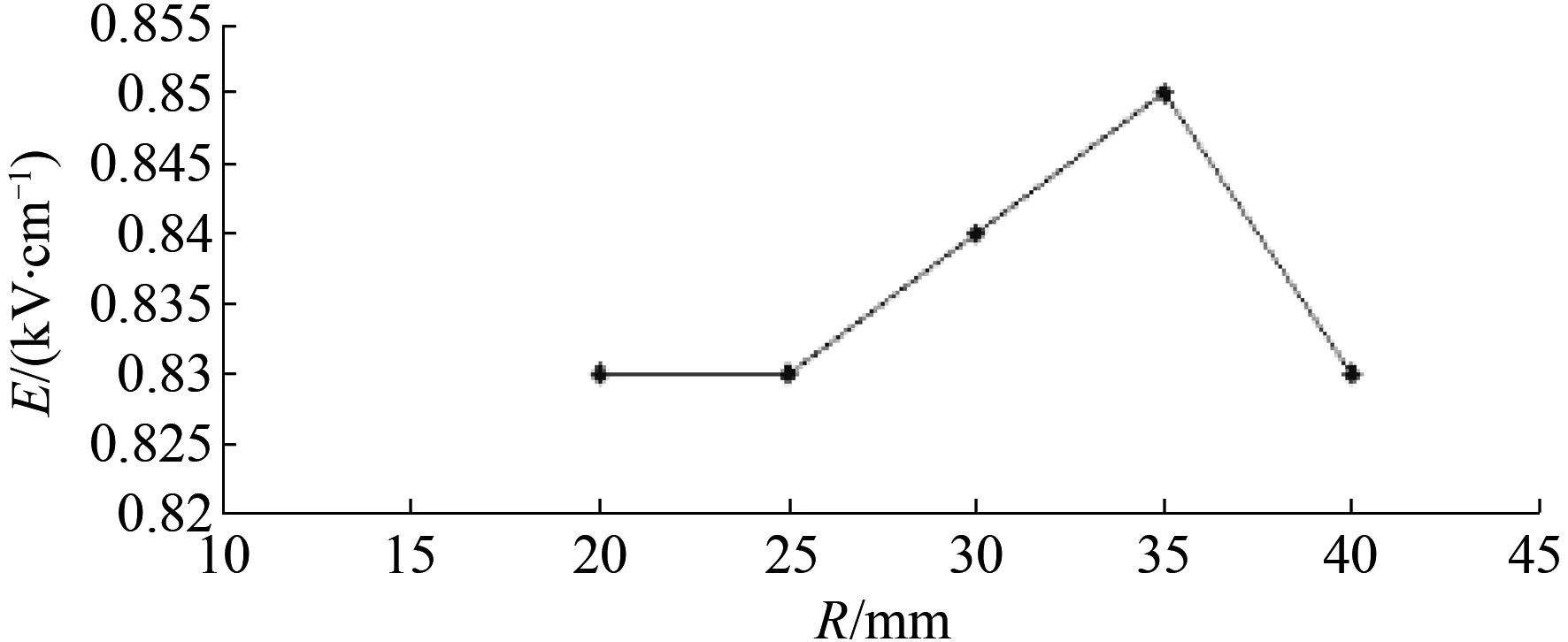
图13 不同半径内电极球最大电场强度分布图

不同半径内电极球绝缘子模型附近电场强度分布云图见图14。

图14 不同半径内电极球绝缘子电场强度分布云图

从表4和图13中可以看出，绝缘子内电极球半径增大，绝缘子附近最大电场强度变化很小，也就是说绝缘子内电极球半径不是影响绝缘子附近最大电场的关键因素。从图14可以看出，绝缘子内电极球半径的变化对绝缘子外部电场强度均匀程度影响不大，其主要影响绝缘子内部的电场强度大小以及均匀程度，内电极球半径越大绝缘子内部平均电场强度越大，这对绝缘子来说是不利的，因此内电极球半径不可以太大，其大小应当控制在一定的范围内，具体范围的确定有待进一步研究。

4.2 内电极杆半径的影响

建立如图15所示的绝缘子模型，其中内电极杆半径不同，内电极球半径相同，均为20 mm，仿真结果见表5。

图15 内电极的杆径不同的绝缘子模型示意图

仿真计算结果见表5。

表5 内电极的杆径不同的绝缘子模型最大电场强度

从表5数据可以得出，杆径越大绝缘子表面电场强度越大，虽然变大幅度不是很大，但是依然对绝缘子来说是不利的，太细的杆径可能无法承受导线以及绝缘子的作用力，因此设计时两者都得保证。

内电极杆径不同的绝缘子模型附近电场强度分布云图见图16。

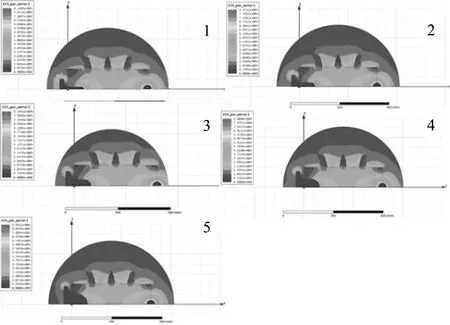
图16 内电极的杆径不同的绝缘子模型电场强度分布云图

从图16可以得出，绝缘子内电极杆径对绝缘子附近平均电场强度影响不大。

5 结语

(1)绝缘子伞棱的形状对其表面电场强度影响不大，但伞棱的多少及其有无影响绝缘子附近平均电场强度的大小。绝缘子伞棱越少，绝缘子附近电场强度越均匀。

(2)内、外电极同时使用对绝缘子表面电场分布确有改善但效果有限，且耗费材料更多，使用时应虑及经济性确认是否需要。

(3)绝缘子长度越长，最大电场强度明显减小，同时绝缘子附近平均电场强度也会减小，并且对靠近杆塔侧的绝缘子承担电压降低效果比导线侧更明显。

[1]司马文霞，杨庆，孙才新.基于有限元和神经网络方法对超高压合成绝缘子均压环结构优化的研究[J]. 电机工程学报，2005,25(17):115-120.

SIMA Wenxia, YANG Qing, SUN Caixin, et al. Optimization of corona ring design for EHV composite insulator using finite element and neural network method[J]. Proceedings of the CSEE,2005,25(17):115-120.

[2]邓铭, 王世山, 李彦明, 等.基于非对称故障条件的复合绝缘子电场分析[J].电瓷避雷器，2004(3):4-7.

DENG Ming, WANG Shishan, LI Yanming， et al. Electric analysis of composite insulator based on asymmetrical faulty condition[J].Insulators and Surge Arresters,2004(3):4-7.

[3]曾庆禹,特高压输电线路电气和电晕特性研究[J].电网技术，2007,31(19):1-8.

ZENG Qingyu. Study on electric characteristic and corona performance of UHV AC transmission line[J].Power System Technology,2007,31(19):1-8.

[4]张忠亭. 架空输电线路设计原理[M]. 北京：中国电力出版社, 2010.

[5]CEI/IEC 60826(2003). Design criteria of overhead transmission lines[S]. Geneva, Suisse.

[6]GB 50061—2010 66 kV及以下架空电力线路设计规范[S]. 中国电力企业联合会.

[7]屠志健，张一尘. 电气绝缘与过电压[M]. 北京：中国电力出版社, 2009.

[8]许颖，徐士珩. 交流电力系统过电压防护及绝缘配合. 北京[M]：中国电力出版社, 2006.

[9]Shigeru Yokoyama, Lightning Protection of Overhead Power Distribution Lines[J]. IEEE Transactions on Electrical and Electronic Engineering. 2007,2(5):491-496.

[10]交流电气装置的过电压保护和绝缘配合：DL/T 620-1997[S].

[11]武利会. 影响绝缘子雷电冲击特性的因素分析[J]. 广东电力 2008,21(5)：23-25.

WU Lihui. Analysis of factors affecting lightning impulse characteristic of insulators[J]. Guangdong Electric Power,2008,21(5):23-25.

[12]严璋，朱德恒. 高电压绝缘技术[J]. 北京：中国电力出版社，2007.

[13]刘国强，赵凌志，蒋继娅. Ansoft工程电场场有限元分析[M]. 北京：电子工业出版社，2005.

(本文编辑：赵艳粉)

Optimum Selection of 10 kV Inside Cementing Porcelain Insulator

AN Shuai, WU Hao, CHAI Jun

(State Grid Shibei Power Supply Company, SMEPC, Shanghai 200072, China)

The 10 kV distribution line insulator is an important equipment that can form the isolation between lines and the ground potential. This paper studied some the typical factors influencing the electric field intensity distribution of 10 kV inside cementing porcelain insulator, such as the length of the insulator, insulator sheds′ number and shape , the shape of the inner electrode. In conclusion, the insulator sheds had a very small influence on the maximum electric field intensity of insulator; the length of the insulator influences the insulator′s maximum electric field intensity: the longer the insulator is, the smaller maximum electric field intensity the insulator has; the inner electrode′s radius of insulator had a very small impact on the maximum electric field intensity of insulator, however, the bigger the rod diameter of the inner electrode of insulator is, the larger the maximum electric field intensity on the surface of the insulator became. These calculation results can provide theoretical basis for the inside cementing porcelain insulator designer and help optimize design scheme.

10kV distribution line; porcelain insulator; electric field intensity

10.11973/dlyny201703010

安 帅(1987—)，男，硕士，工程师，从事电网电磁场研究。

TM854

A

2095-1256(2017)03-0258-05

2017-02-15