煤粉通气料仓的优化设计
2017-07-01陆海峰郭晓镭
付 琳, 陆海峰, 郭晓镭, 龚 欣
(华东理工大学煤气化及能源化工教育部重点实验室,上海市煤气化工程技术研究中心,上海 200237)
煤粉通气料仓的优化设计
付 琳, 陆海峰, 郭晓镭, 龚 欣
(华东理工大学煤气化及能源化工教育部重点实验室,上海市煤气化工程技术研究中心,上海 200237)
料仓通气技术具有成本低、噪音小的优势,被广泛应用在黏附性粉体下料过程中。为确定黏附性煤粉下料过程的最优通气条件,在自行搭建的有机玻璃料仓上进行煤粉的通气下料实验。实验结果表明,通气可以显著促进煤粉下料,但通气高度和通气气速对下料过程的影响存在耦合作用。以气泡运动理论为基础,结合气泡与颗粒间的相对运动关系,建立了煤粉通气下料模型。基于实验数据关联气泡尺寸与通气高度及通气气速间的关系,通过模型分别计算了最优相对通气高度H/D=12.25和最优通气气速Ug=2.4Umf。模型计算值与实验值的吻合效果良好,当5.56
煤粉料仓; 优化; 通气气速; 通气高度; 下料流率
下料过程广泛地存在于粉体的气力输送领域,也是气流床煤粉加压技术中的重要单元[1]。其中,通气是常用的辅助下料方式,尤其适用于含水量较低的粉体。粉体的下料过程涉及气固相互作用,使粉体的流动表现出高度的复杂性。对于粒径较小、流动性较差的粉体,颗粒间的黏聚力也成为影响下料的因素[2],增加了理论研究的难度。文献[2-3]分别从通气流动方向及颗粒受力角度,建立了适用于无黏性粉体的通气下料预测模型。Lu等[4]利用上述模型计算黏附性煤粉下料流率时发现计算结果偏大。Barletta等[5]通过测量团聚体的相关特性,修正了Donsi方程,使之适用于黏附性粉体的通气下料情况,但模型计算所需的粉体团聚参数较难获得。Huang等[6]通过实验得出适用于煤粉通气下料的经验方程,但当物料改变时,方程的计算误差较大。
文献[7]通过对通气位置及气速的合理选择的研究发现,在一定气速范围内,下料流率随气速的增加而增大;当气速超过一定程度时,下料流率不再提高。对于锥形料仓,较大的气速还会出现下料停滞,即产生气压平衡拱[8]。Huang等[6]指出,通气高度越低,出现气压平衡拱的频率越高,强度越大。Du等[9]认为提高通气高度可以增大出料口附近的压力梯度,增大下料流率,但通气高度过高容易使通气位置上方的床层崩塌,造成出料口的堵塞。
通气下料过程存在最优通气条件,但目前尚缺少相应的方法给出明确的最优值。本文基于有机玻璃料仓下料系统,研究了通气高度、气速对煤粉通气下料过程的影响;另外基于实验现象提出以壁面气泡关联通气速度、通气高度的优化方法;对于本实验系统,模型能够预测实验点的变化趋势,并能确定煤粉的最佳通气条件。
1 实验部分
1.1 实验装置
图 1(a)所示为实验流程,主要包括供气、下料、接料3个部分。下料前通过气体质量流量计控制进入有机玻璃料仓的气速,所用气体为干燥过的压缩空气,待床层状态稳定后开启下料阀,使物料落至钢质接料罐中,下料完成后,向接料罐中通气充压至70 kPa,开启输送阀,物料再次被输送到料仓中。
料仓的结构尺寸如图 1(b)所示,出料口直径D=40 mm、半锥角θ=15°。P代表壁面上的压力传感器,用L代表料仓锥部的线式通气结构,L1~L5代表由低到高的不同位置。线式通气由锥部壁面上处于同一高度的6个通气孔组成。

1—Air compressor;2—Drying machine;3—Gas distributer;4—Gas mass flowmeter;5—Receive vessel;6—Pressure transducer;7—Dust filter; 8—Load cell;9—Fluidization hopper图 1 实验流程与料仓结构示意图Fig.1 Experimental process and structure of the hopper
1.2 实验物料
以晋城煤为实验物料,其基本物性参数如表1所示。图2展示了晋城煤的粒径分布情况,主要分布于粒径小于100 μm的范围内。根据Geldart等[10]有关颗粒密度和粒径间的相互关系,将粉体划分为A、B、C、D 4大类。结合表 1中的煤粉的颗粒物性参数可知,本文所用晋城煤属于A类粉体,流化状态较为稳定,充气时不容易出现沟流、节涌等问题。此外,本文还采用HR (Hausner Ratio)指数来描述粉体的流动状态。表1中晋城煤HR指数为1.67,处于1.4~2.0之间,表明其流动性较差且具有一定黏附性[11]。
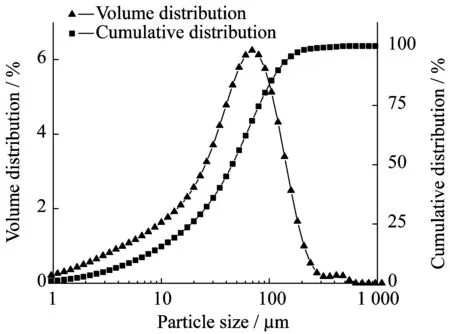
图2 晋城煤粉粒径分布Fig.2 Particle size distribution of Jincheng coal

Pulverizedcoaldv/μmρp/(kg·m-3)ρb/(kg·m-3)w(Totalmoisture)/%HRGeldartgroupJinchengcoal66.361627.5580.61.271.67A
2 结果与分析
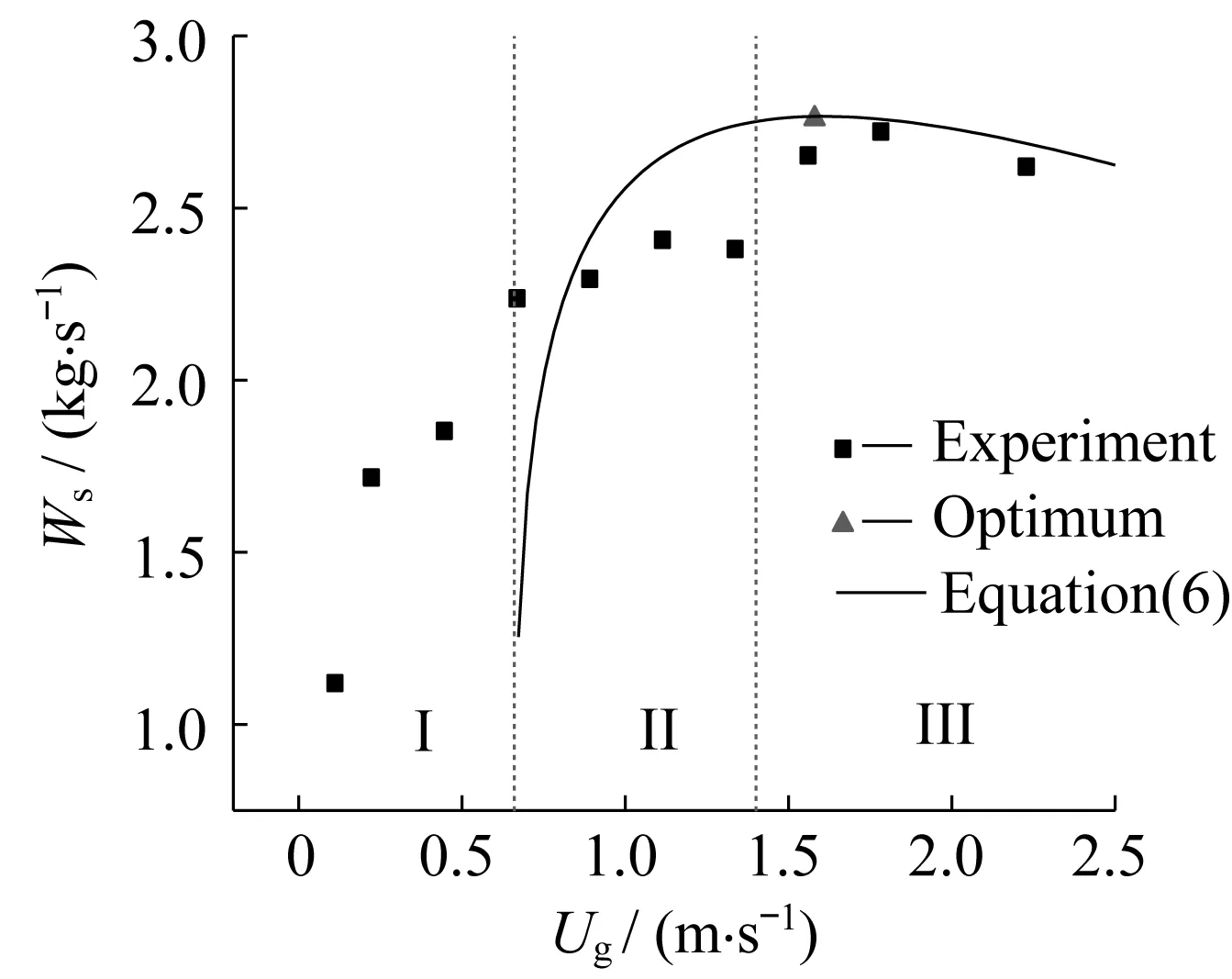
实验通过调节通气气速Ug及通气高度H控制通气条件进行煤粉料仓通气下料。图3显示了当通气条件改变时晋城煤在通气料仓内下料流率的变化情况。可以看到Ug与H对下料流率Ws的影响具有一定耦合性,单独提高Ug总体表现出对下料的促进作用,提高H则表现出对下料的抑制作用,两者共同作用导致在高位低速及高位高速通气情况下煤粉的流动性质没有明显的改善。
整体而言,通过分析Ws随Ug的变化规律可将图3分为3个区域:在I区内Ug增大,Ws快速增加;II区内Ws趋于平稳,Ug对下料的影响减弱;在III区内,Ug的升高总体表现为对下料的抑制作用。依据Lu等[12]对不同区域煤粉下料特性的分析可知,上述分区反映出通气后床层分别经历了局部流化、拟整体流化及鼓泡流化3种状态。参考流态化的相关理论,依据图3中I、II区及II、III区域间的临界Ug可近似地给出晋城煤的相关特征气速,即:最小流化速率Umf=0.67 m/s、最小鼓泡气速Umb=1.40 m/s。需要说明的是,上述特征气速可有效反映煤粉通气下料的状态特征,但尽管通气料仓与流化床具有一定的相似之处,然而两者并不相同,因此该特征气速并不能代表其在流化床内的实际状态。

图 3 不同通气位置处煤粉的下料曲线Fig.3 Discharge rate of pulverized coal at different aeration locations
3 最优值理论分析
3.1 最优通气高度的计算
Brown等[13]、Donsi等[2]认为下料时在出料口上方存在理想拱面,下料流型在拱面处发生改变:拱面上方为颗粒流区,下方为悬浮流区。陶顺龙等[14]通过实验证明在通气下料过程中同样存在流型转变的理想拱面。假设该拱面稳定于仓内某一高度HG,拱上方颗粒向下流动,与悬浮流区存在相对运动,颗粒流过拱面速率为Us;若假设拱上方颗粒为静态,则悬浮流区域在仓内相对上升,上升速率为u,该速率与颗粒流过拱面的速率Us大小相同、方向相反。参考气泡在床层内的上升过程,可以得到锥形料仓的下料流率表达式:

(1)

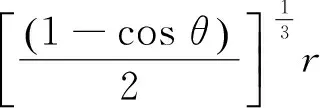
(2)
料仓内煤粉重力下料流率为0.89kg/s,代入式(1)得到r=10.30cm,dq约为2.65cm。对于锥角及出口直径较小料仓,HG近似与r相等。通气高度H与料仓出口直径D的比值(H/D)可以表示通气高度的相对位置[6,21],则理想拱面的相对高度HG/D为2.57。
图3表明煤粉通气下料的最优通气位置为L3,对应拱面上方的颗粒流区。分析式(1)可知Ws增加时,r必然增加,说明相比于重力下料过程,通气使仓内悬浮流区域扩大,上表面积S增加,从而促进下料。Cannavacciuolo等[17]认为,通气能引起仓内稳定结构的崩溃,提升理想拱面高度直至达到新的平衡条件。因此,设想在通气均匀及颗粒间无作用力的理想条件下,通气后动态拱面上升至通气孔所在高度,通气的流化作用使颗粒流向悬浮流转变。
下料时粉体料仓内的颗粒速率分布不均匀,靠近中部流速最快,靠近壁面流速最慢[18],与管道中理想流体层流流动的速率分布相似,类比管道中流体层流流动平均速率的计算方法,颗粒流过理想拱面的平均速率Us等于中心速率的1/2[19]。实验证明过量通气对下料起阻碍作用。假设这是由于通气在通气孔附近壁面上产生气泡,压缩下料转换面区域导致的。由此可知,在通气孔所在高度上,靠近壁面处气泡在静止的颗粒床层中上升,靠近中部颗粒在静止的气体中下落。在料仓的壁面与中部,气体与颗粒间的相对运动是一致的。可近似认为壁面气泡的上升速率uw等于中心颗粒的下落速率。图3给出了理想条件下,通气后仓内粉体的床层状态:拱面由S上升至S′;通气产生壁面气泡,提高颗粒下落速率的同时限制拱面大小。由上述分析,对式(1)的S及Us进行修正,最优通气高度上下料流率的计算方法为:
(3)


图 4 理想化的煤粉床层最佳下料状态Fig.4 Idealized optimal discharging condition of pulverized coal bed
式(3)可表示成与rw有关的形式,在确定rw与通气条件及Ug的关系式后,可对通气条件进行定量选择。首先确定H对Ws影响,表2所示为所选下料的工况,气速满足Ug>Umf。表3给出了由表2中的下料流率反推得到的rw,拟合rw与H平均值间的关系得到:
rw=0.157H1.73

表2 典型气速下不同高度的实际下料流率

表3 典型气速下不同位置的计算壁面气泡半径
图 5所示为拟合结果,可以看到式(4)对实验值的拟合效果良好,满足定量计算要求。联立式(3)、(4)得到Ws。
Ws=1 599.8(0.268H+0.02-0.309H1.73)2H0.86
(5)
求导式(4)得到最优相对通气高度H/D=12.25,对应最大下料流率3.07 kg/s。实验得到的最优相对通气高度H/D=12.15,最大下料流率2.69 kg/s。最优相对通气高度与实验值的偏差为1.23%。模型预测相对高度与Lu等[12]的建议相对高度(11.40)偏差为6.17%,与Huang等[6]通过实验确定的最优相对高度(10.25)偏差为16.23%,说明模型所提供的通气高度优化方法对黏附性粉体较为适用。
式(5)将Ws与H间离散的实验点表示成连续的变化关系,图6给出了模型预测的总体结果,可以看到模型得到的最优相对通气高度与实验最优值接近。模型曲线与H/D轴交于0、21两点,分别代表无通气及气泡完全封闭下料空间中两种不能下料的情况。当0 3.2 最优通气气速的计算 分析相对高度H/D=12.15处(图3中L3)的通气下料结果可知,在最优通气高度上,增加Ug可提高Ws,以Ws作为衡量煤粉下料的标准,可判断其最优气速出现在III区内,即Ug>1.40 m/s。利用Darton等[20]方程可确定rw与Ug的关系,方程的适用条件为Ug>Umf。选择H/D=12.15的系列实验中气速Ug>Umf(Umf=0.67 m/s)部分的数据,结合式(3)计算实际下料过程中的rw。表 4示出了计算结果,拟合其中rw与Ug的关系写成Darton[20]方程的形式得到: 图5 rw与H变化关系的拟合结果Fig.5 Fitting results of the relation between rw and H 图6 最优通气高度计算值与实验值的比较Fig.6 Comparision between calculated and experimental of optical aerated height rw=0.025(Ug-Umf)0.55g-0.2 (6) 表4 壁面气泡尺寸的计算结果 将式(6)代入式(2),结合料仓结构参数及煤粉物性,最优通气高度上的下料流率可表示为: (7) 对式(7)中的Ug进行求导可得到方程的极大值点为:Ug=1.58 m/s=2.4Umf,Ws=2.72 kg/s。处于Lu等[21]、Huang等[6]实验确定的黏附性煤粉下料最优气速分布区间(2.0Umf 图7 L3通气位置处模型预测值与实验值的比较Fig.7 Comparison between model predictions and experimental values on the locations of L3 3.3 模型的优化效果 为客观体现模型的优化作用,将通气条件的模型优化值与实验最优值(文献[6,21]数据、本研究体系)进行比较。由表5可知,模型预测的最佳通气相对高度(量纲为一的H/D)和最佳气速(量纲为一的Ug/Umf)与实验值吻合效果良好,能够有效预测煤粉料仓下料的通气条件。此外,将模型预测值和文献[6,21]的研究结果进行对照同样发现具有较好的吻合度,预测的最佳通气相对高度偏差不超过20%,而最佳气速也在实验范围内。由此可见,模型能够准确预测黏附性煤粉下料时的最优通气条件。 表5 煤粉通气料仓下料最优条件预测 (1) 煤粉的通气下料实验结果表明,气速超过煤粉的最小流化气速后,下料流率的变化趋于平稳,并在L3处出现最大下料流率。由下料流率分区模型分析出煤粉的最小流化速率Umf=0.67 m/s、最小鼓泡速率Umb=1.40 m/s。 (2) 实验证明煤粉的通气下料存在最优通气高度,即L3位置(H/D=12.15)。气速增加有助于提高下料流率,最优气速满足Ug>Umf,实验确定煤粉最小流化气速为Umf=0.67 m/s。 (3) 通过锥口处气体与颗粒间相对运动建立煤粉重力下料模型,得到下料时的动态拱相对高度HG/D=2.57。由观察到的通气下料截面流型,发现通气对颗粒流动的限制作用,引入壁面气泡概念建立煤粉通气下料模型,对比实验结果后发现,对于满足Ug>Umf,5.56 (4) 通过拟合气泡尺寸rw与通气高度H及气速Ug的关系,得到煤粉料仓最优通气条件:最优通气相对高度H/D=12.25,位于动态拱上方的颗粒流区内,与实验值偏差为1.23%;最优气速为Ug=2.4Umf=1.58 m/s,处于实验确定的最优气速区间(1.56~2.22) m/s。 符号说明: dq——悬浮流区的等体积球直径,m dv——体积平均粒径,μm H——通气高度,m HG——悬浮流区高度,m r——理想拱面径向半径,m rw——壁面气泡半径,m S——悬浮流区表面积,m S′——通气后悬浮流区表面积,m2 u——悬浮流区相对上升速度,m/s Ub——颗粒最小鼓泡气速,m/s Ug——通气气速,m/s Umf——颗粒最小流化气速,m/s Us——颗粒流过动态拱面的平均速度,m/s uw——壁面气泡上升速度,m/s Wcal——下料流率计算值,kg/s Wexp——下料流率实验值,kg/s Ws——下料流率,kg/s θ——料仓半锥角,(°) ρb——煤粉的堆积密度,kg/m3 ρp——煤粉的真实密度,kg/m3 [1] 陆海峰,郭晓镭,陶顺龙,等.电容层析成像在煤粉料仓下料中的应用[J].化工学报,2014,65(2):422-429. [2] DONSI G,FERRARI G,POLETTO M,etal.Gas pressure measurements inside an aerated hopper[J].Chemical Engineering Research and Design,2004,82(1):72-84. [3] ALTINER H K.Flow of solids from aerated hoppers:Effect of aeration methods[J].American Institute of Chemical Engineers Symposium Ser,1983,222:55-59. [4] LU Haifeng,GUO Xiaolei,GONG Xin,etal.Study on the fluidization and discharge characteristics of cohesive coals from an aerated hopper[J].Powder Technology,2011,207(1):199-207. [5] BARLETTA D,DONSI G,FERRARI G,etal.Solid flow rate prediction in silo discharge of aerated cohesive powders[J].American Institute of Chemical Engineers Journal,2007,53(9):2240-2253. [6] HUANG Wanjie,GONG Xin,GUO Xiaolei,etal.Discharge characteristics of cohesive fine coal from aerated hopper[J].Powder Technology,2009,194(1):126-131. [7] FERRARI G,BELL T A.Fluidized state processes——Effect aeration on the discharge behaviour of powders[J].Powder Handling and Processing,1998,10(3):269-274. [8] 郑利娇,郭晓镭,代正华,等.粉煤在流化料仓中的下料特性[J].化工学报,2007,58(9):2375-2381. [9] DU S W,LIU T C,CHUNG Y H.A rate model for the discharge of pulverized coal from a pressurized aerated-tank[J].Powder Technology,1989,57(1):69-75. [10] GELDART 1D,ABDULLAH E C,HASSANPOUR A,etal.Characterization of powder flowability using measurement of angle of repose[J].China Particuology,2006,4(3-4):104-107. [11] CARNAVAS P C,PAGE N W.Particle shape factors and their relationship to flow and packing of bulk materials[J].Mechanical Engineering Congress,1994,2:241-246. [12] LU Haifeng,GUO Xiaolei,GONG Xin,etal.Experimental study on aerated discharge of pulverized coal[J].Chemical Engineering Science,2012,71:438-448. [13] NEDDERMAN R M.Statics and Kinematics of Granular Materials[M].New York:Cambridge University Press,2005. [14] 陶顺龙,陆海峰,郭晓镭,等.煤粉料仓通气下料流动行为[J].化工学报,2014,65(4):1186-1193. [15] DONG Liang,ZHAO Yuemin,LUO Zhenfu,etal.A model for predicting bubble rise velocity in a pulsed gas solid fluidized bed[J].International Journal of Mining Science and Technology,2013,23(2):227-230. [16] 洪勇.粉体力学与工程[M].北京:化学工业出版社,2003. [17] CANNAVACCIUOLO A,BARLETTA D,DONSI G,etal.Arch-free flow in aerated silo discharge of cohesive powders[J].Powder Technology,2009,191(3):272-279. [18] SNIDER D M.Three fundamental granular flow experiments and CPFD predictions[J].Powder Technology,2007,176(1):36-46. [19] 黄卫星,李建明,肖泽仪.工程流体力学 [M].北京:化学工业出版社,2009. [20] DARTON R C.Bubble growth due to coalescence in fluidized bed[J].Chemical Engineering Research & Design,1977,55:274-280. [21] 陆海峰.煤粉在通气料仓中的下料及其影响因素研究[D].上海:华东理工大学,2012. Optimization Design of Pulverized Coal Discharged from an Aerated Hopper FU Lin, LU Hai-feng, GUO Xiao-lei, GONG Xin (Key Laboratory of Coal Gasification and Energy Chemical Engineering of Ministry of Education,Shanghai Engineering Research Center of Gasification Technology,East China University of Science and Technology,Shanghai 200237,China) The silo aeration technology,which has the advantage of low cost and low noise,has been widely used in discharging adhesive powder.The experiment of aerated discharging of pulverized coal was carried out in the self-built plexiglass hopper for determining the optimal aerated condition during the pulverized coal discharging.The result showed that aeration could promote the discharging remarkably,however,the influence of aerated height and velocity existed coupling effect.On the basis of the theory of bubble motion,the model of pulverized coal discharging was built considering the relative motion between bubbles and particles.The relationship between bubble size and aerated condition was associated based on the experiment.The calculated optimal height wasH/D=12.25 and the optimal velocity wasUg=2.4Umf.There was a good agreement between calculation and experiment.The deviation of calculated discharging rate was less than ±20% while 5.56 pulverized coal hopper; optimization; aerated velocity; aerated height; discharging rate 1006-3080(2017)03-0297-07 10.14135/j.cnki.1006-3080.2017.03.001 2016-10-11 国家自然科学基金(21206041);中央高校基本科研业务费专项资金资助(222201717004);上海市科委科研计划项目(15dz1200802) 付 琳(1991-),男,黑龙江鸡西人,硕士生,研究方向为煤气化。E-mail:pof_lin@foxmail.com 陆海峰,E-mail:luhf@ecust.edu.cn TQ536 A



4 结 论
