一种复杂机电系统LE-SVDD异常监测方法

2017-07-01亚森江加入拉高建民高智勇姜洪权陈子胜

振动、测试与诊断 2017年3期

关键词：漏报降维样本

亚森江·加入拉，高建民，高智勇，姜洪权，陈子胜

(1.西安交通大学机械制造系统工程国家重点实验室西安，710049)(2.新疆大学机械工程学院乌鲁木齐，830046)

一种复杂机电系统LE-SVDD异常监测方法

亚森江·加入拉1，2，高建民1，高智勇1，姜洪权1，陈子胜1

(1.西安交通大学机械制造系统工程国家重点实验室西安，710049)(2.新疆大学机械工程学院乌鲁木齐，830046)

复杂机电系统生产过程监测数据具有明显的高维非线性和复杂分布特点，针对传统的方法难以满足复杂系统异常辨识的要求，提出一种拉普拉斯特征映射-支持向量数据描述(Laplacian eigenmaps-support vector domain description，简称LE-SVDD)的异常监测方法。由于高维特征空间中距离很近的点投影到低维空间后距离应该很近，因此改进的LE方法使用一个有权无向图来描述一个流行，用嵌入的方式找到高维数据的低维嵌入，从而能够发现高维数据内部的地位流行结构。通过标准的田纳西-伊斯曼过程(Tennessee Eastman process，简称TE过程)测试和训练数据进行仿真实验，给出了在非线性特征提取和不同时段异常辨识的准确结果。平均漏报率和误报率都比较低，分别为6.063，6和5.625，3.125，这表明LE-SVDD方法在状态监测中具有良好的非线性和高维数据处理能力，适用于工程系统的监测诊断。

复杂机电系统；异常监测方法；特征提取；拉普拉斯特征映射-支持向量数据描述(LE-SVDD)；田纳西-伊斯曼(TE)过程

引言

化工生产系统是有诸多大型机电和化工设备组成的庞大且分布式复杂系统，是典型的流程工业系统。对生产过程状态有效地进行监测并及时排除故障因素是保证企业安全生产、提高产品质量和经济效益的重要手段。在复杂机电系统这一特殊的设备群中，使用一种有用而合适的状态监测方法具有非常重要的研究意义。

国内外学者提出的状态监测方法很多。Frank以先验知识为基础，将故障诊断方法分为三大类，分别为基于解析模型、基于专家知识的定性分析方法以及基于数据驱动的分析方法[1]，但是针对的都是特定的问题，未能考虑到系统的复杂性特性。对于复杂机电系统，由于难以建立准确的数学模型，因此限制了基于模型的监测诊断方法的应用。在理论上，目前数据挖掘理论逐渐成熟，神经网络、支持向量机、一致性预测与支持向量随机描述等方法逐渐在故障诊断领域被应用[2-4]。文献[5]提出了基于SVDD的机械故障的单分类新方法。如果目标分类是有效的，该方法在离群值类未知情况下能够区别离群值对象和目标对象。文献[6]对凝汽器结污(condenser fouling,简称CdF)和制冷剂泄漏(refrigerant leakage，简称RfL)两种故障情况提出了主成分分析-残渣-支持向量数据描述(principal component analysis-residual-support vector domain description，简称PCA-R-SVDD)基础模型。与传统的方法相比较，提出的方法具有更好的故障数据分布和更严格的统计检测能力。其他相关的研究成果同样采用基于改进的SVDD方法，由于使用领域和设备不同，因此改进的优化方法也有所不同[7-10]。虽然这些方法充分考虑了非线性因素并较好地解决了因相关性造成的信息冗余，但是针对的是单台设备或较简单的工业过程，未能充分考虑到流程工业系统的复杂性特性。

复杂机电系统生产过程监测数据具有明显的高维非线性和分布复杂的特点，因此传统的线性方法PCA和基于高斯分布假设核主元分析方法(kernel principal component analysis，简称KPCA)的故障监测方法难以满足复杂机电系统异常状态监测的要求。虽然KPCA能够有效提取原始数据的非线性特征，但是核方法处理效果的好坏一方面依赖于核函数的类型，另一方面受核参数的影响。核函数通常选取常用的几类核函数形式，核参数的选取无科学的理论指导，目前尚未出现有效的解决方法。

为了适应复杂机电系统模式的复杂性和多样性，解决非高斯分布样本的异常监测问题，笔者提出一种基于特征样本建模的复杂机电系统LE-SVDD异常监测方法。对海量数据进行降维，用获得的特征样本来建立监测模型，从而判断系统的故障模式。

1 拉普拉斯特征映射

拉普拉斯特征映射(LE)是一种流行学习方法[11]，是局部线性嵌入(locally-linear embedding,简称LLE)方法的一个变种，其基本思想是在高维特征空间中距离很近的点投影到低维空间后距离也应该很近，使用一个有权无向图来描述一个流形，通过图嵌入的方式找到高维数据的低维嵌入。流形属于拓扑学上的一个概念，表示一个局部处于欧几里得的空间，该空间上任意一点都存在一个邻域，在该邻域内，拓扑结构与空间中的单位圆相同。假设高维空间Rd中的样本数据集X={x1,x2,…,xn}，xi∈Rd(i=1,2,…,n)，xj∈Rd(j=1,2,…,n)，且xi≠xj，高维样本数据点xi和xj在原始空间中是距离较近的两个样本点，即xj是xi的k个近邻点之一，点xi和xj之间的欧式距离定义为d(i,j)。LE方法基于图谱理论，使用一个正的权值Wij来联系点xi和点xj，通常使用热核函数来设置权。热核函数定义如下

(1)

其中：σ2为比例参数。

LE构造的低维空间嵌入目标函数为

(2)

在满足流形结构对域的约束yTDy=1和单点约束yTDy=0基础上，最小化目标函数，求解步骤相当于求解式(3)的最小特征值问题

Ly=λDy

(3)

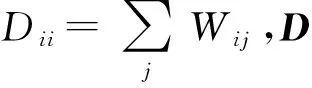
LE算法计算步骤总结如下。

1) 输入样本X={x1,x2,…,xn}，xi∈Rd(i=1,2,…,n)，近邻点数为k，计算每个点xi的k个最近邻点，1≤i≤N。

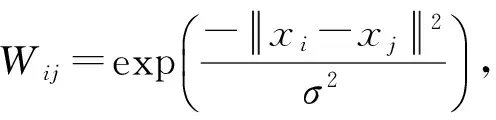
3) 求解目标函数的最小误差，相当于求解拉普拉斯算子的广义特征向量问题：求得式(3)最小r个非零特征值对应的特征向量{φ1,φ2,…,φr}，嵌入结果表示为T=[φ1,φ2,…,φr]T。

从拉普拉斯特征映射的算法推导可知，拉普拉斯特征映射只需要很少的计算量，因此算法速度在流形学习的若干算法中最快。Belkin和Niyogi在理论上证明了LE算法的收敛性。流形学习的目标是寻找数据集中的内在关系，发现高维数据集存在的低维流形特征，将观测数据在低维嵌入空间中进行展开，在保证数据流形结构不变的前提下实现数据降维。在目前常用的流形学习算法中，仅需要指定几个变量即可实现数据的非线性降维，同时参数对于降维效果的影响较小，这样就避免了核方法参数选取困难的问题。

2 SVDD算法

SVDD是Tax[12]基于支持向量机(support vector machine,简称SVM)提出的一种单类数据分类算法。其思想是将目标样本作为整体，在特征空间寻找一个超球面对目标样本全部或尽可能多的包裹，以结构风险为目标对超球面大小进行优化，并对未知数据进行分类。

假设Rd空间存在样本集X={x1,x2,…,xn}，n为样本数目，存在这样一个非线性的映射函数φ，可以将样本x映射为高维特征空间F中的Φ(x)，即

φ:x→Φ(x) (x∈Rd,Φ(x)∈F)

(4)

目标是最小化结构风险，即在特征空间F中寻找一个最小的超球面，使得该超球面能够尽可能地包裹{Φ(xi)}(i=1～n)中的特征样本点。图1为SVDD算法示意图。

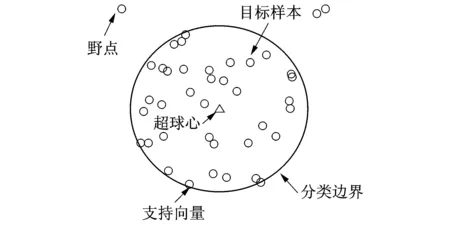
图1 SVDD算法示意Fig.1 SVDD Algorithm diagram

SVDD算法与SVM类似，可以定义误差函数最小化

F(R,a)=R2

(5)

约束为

‖xi-a‖2≤R2, ∀i

(6)

为了允许异常值在训练集总存在，从xj到a的中心距离与R2不应该完全一样。大一点的距离应该不利计算和辨识。因此这里引入松弛变量ζi≥0，最小化问题改为

(7)

其中：C为控制错分的惩罚参数。

球体之内所有对象的约束条件为

‖xi-a‖2≤R2+ζi(ζi≥0，∀i)

(8)

其中：a为超球心坐标；R为超球心到边界距离；ζi≥0为松弛变量。

约束条件(8)使用拉格朗日泛函(Lagrange multiplier)并入式(7)得到

(9)

其中：ai≥0；λi≥0。

考虑到R,a,ζi时，L应该是最小化；考虑到αi,γi时，L应该是最大化。

SVDD中通常选取高斯核。在计算时，处于超球面上的样本点满足条件0≤ai≤C，这些点就是支持向量(support vector,简称SV)，超球球心a与半径R由这些SV确定。

对于一个测试样本点xtest，首先计算该点与超球心的距离

(10)

如果D≤R2，则接受测试点为目标点，否则拒绝为目标点。

3 基于特征样本的LE-SVDD监测方法

针对实际系统中存在的信号含噪和高维两种问题，对降噪后的数据采用流行学习LE方法进行降维，提取特征样本，以特征样本代替原始数据进行建模，降低SVDD算法的复杂度。通过LE和SVDD组合应用，并基于特征样本的监测方法应用于本研究中。

3.1 SVDD训练样本降维的必要性

实际工业系统监测点位众多，为了保证计量数据的正确性，同一监测点位可能安装若干计量设备，因此采集到的历史数据集中就产生了大量的冗余信息。当以这样一种数据集进行建模时，训练样本的采样总数可能数以万计，且单一训练样本又具有较高维度，这时冗余信息及对特征影响小的分量信息就会对建模产生较大影响，从而影响识别效果。

对训练样本降维存在若干好处，其中最重要的一点是会使算法建模复杂度减少并提升识别效果。这是因为约简训练样本维度不仅会消除冗余信息造成的影响，同时会解决海量数据带来的维数灾难问题。另外，维度约简过程可获取设备状态的主要影响因素，使得模型能够更好地被理解。

分析现有的数据挖掘模型，用于数据维数约简的方法可归纳为两种：特征选择及特征提取。特征选择能剔除不相关或冗余的特征，从而达到减少特征个数、提高模型精确度的目的。其计算过程是在全部特征集中产生一个特征子集，然后用评价函数对特征子集进行评价，采用模拟退火、遗传算法等算法对过程进行优化，直到挑选出符合评价指标的结果。但是该方法计算时间较长，且提取的特征并非是一成不变的，因此不适应于在线监测。流形学习等数据特征提取方法是对原始数据进行空间投影，把n维原始数据映射为m维特征数据，计算时间短，能够处理非线性数据，因此在SVDD建模过程前的训练样本维数约简采用特征提取方法处理。

SVDD方法的训练过程实际上就是求解凸二次规划问题，凸二次规划问题的计算复杂度为O(n3)，因此降低训练样本维度将会大大减少模型训练时间，降低了算法对计算机内存和运算时间的要求。

3.2 特征样本LE-SVDD建模步骤

特征样本建模的LE-SVDD异常监测方法与原始SVDD异常状态监测方法的不同之处在于：新方法使用了流形降维后的特征样本建立监测模型；而传统SVDD方法直接使用原始数据。

离线训练时，首先，对训练样本进行小波包分解重构，消除高斯噪声影响，对消噪后的数据进行指数加权移动平均；然后，对处理得到的数据归一化，消除量纲影响，记录训练样本的均值和方差，对归一化后的数据进行非线性降维，减少SVDD算法的计算复杂度，节省计算和存储资源；最后，使用降维得到的特征样本进行LE-SVDD建模，对异常样本进行监测。

在线监测时，采集新的数据样本，进行归一化，利用LE算法的线性近似映射矩阵求得降维后的低维样本点，计算低维样本点与SVDD超球中心的距离。若处在SVDD超球面外，则可判定为系统状态发生异常，后续转入系统异常状态识别阶段；否则认为系统处于正常工况条件，继续对系统状态进行监测。基于特征样本SVDD的系统状态在线监测流程如图2所示，可分为离线建模及在线监测两部分。

图2 特征样本LE-SVDD状态监测流程图Fig.2 Characteristic sample LE-SVDD condition monitoring flow chart

算法步骤如下：

1) 获取训练样本X={x1,x2,…,xn}，xi∈Rd，小波包分解去噪，进行指数加权移动平均，归一化消除量纲影响；

2) 使用LE对处理后的数据进行非线性降维，获取特征样本集，计算线性近似映射矩阵T；

3) 在特征样本集上进行SVDD建模；

4) 对于新进数据进行归一化处理，投影后得到特征空间样本Y=Tx，监测是否超出判定值。

3.3 状态监测结果评价标准与指标

为了保证复杂机电系统状态监测效果的准确性和有效性，首先要确定评价标准。笔者通过对比选用最优的参数作为标准，参考的数据信号包括温度、压力、振动和流量等。

流程工业复杂系统状态监测模型的建立依赖于预先提取的系统正常工况下的离线历史数据。为了给出一种可信的综合性故障或异常监测评价指标，兼顾统计学中的两种错误类型，使用异常状态下的漏报率(missed detection rate，简称MDR)及正常工况下的误报率(false alarm rate，简称FAR)作为衡量监测结果可信度的指标。

MDR和FAR的数学表达式为

(11)

其中：NN,F为测试样本集中正常状态数据被判定为异常点的个数；NM为测试样本集中异常状态数据被判定为正常点的个数；NN为测试样本集中正常样本总数；NF为测试样本集中异常样本总数。

4 仿真实验

4.1 TE过程故障模式

TE过程是以Eastman化学公司的一个实际生产流程为基础提出的一个标准测试过程[13]，它是一个分布式复杂机电系统的典范，包括5个主要操作单元：反应器、冷凝器、汽液分离器、循环压缩机和汽提塔(解吸塔)。

TE过程一共预设了21种故障模式。这些故障模式内故障(identity value，简称IDV)中的IDV(3)，IDV(9)，IDV(15)对于数据变化影响较小，多元统计方法对于这几种故障的检出率很低，本研究就不再将这几种故障模式作为仿真对象。TE过程故障如表1所示。

表1 TE过程故障

4.2 异常监测效果对比

本研究仿真中选取了故障5，10，16和20共计4种故障模式作为研究对象，进行若干组实验，对比组合方法和单一方法在异常状态识别效果上的差别。由于训练样本进行归一化并消除量纲影响，因此以下分析图中均无量纲。

1) 图形对比。首先，使用传统SVDD方法进行异常状态监测。核函数采用高斯核函数，核参数取值为18，各故障模式的异常检出效果如图3所示。从图中可以看出，传统SVDD方法对于第5类故障能够在故障出现的第一时刻监测到异常状态的发生，但是过了一段时间之后，又无法监测到异常；而对于故障10，16，20的识别效果很不理想。

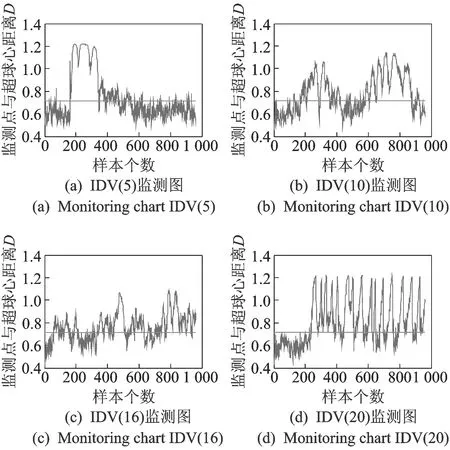
图3 基于SVDD的故障监测效果图Fig.3 SVDD-based fault monitoring effect picture

出现上述结果是因为故障5由冷凝器冷却水入口温度发生阶跃性变化引起的。故障5是一类对过程影响较小的故障模式。控制系统通过调节冷却水的流量变化对系统进行补偿控制。大约在第360个采样点开始，补偿起到调节作用，将变量值恢复到正常值，但是故障确实是存在的，因此故障5的异常监测失效。其他几类故障模式的监测虽未失效，但漏报率和误报率均较高。综上所述，单独使用SVDD方法对TE过程进行异常监测未取得良好效果。

为了得到更准确的异常状态识别结果，按照以上提到的特征样本LE-SVDD监测方法步骤，重新对上述所选故障模式进行状态预测。这里SVDD仍然选取与之前相同的核函数形式及核参数大小，数据处理及消噪方法也完全相同。

实际工业过程监测变量因存在关联性，使得当前时刻的系统状态会收到历史数据影响，因此，在系统出现异常或故障时，异常状态会随着时间进行推移。指数权重移动平均(exponentially weighted moving average，简称EWMA)是一种常见的处理工业系统动态行为的方法。对数据进行EWMA处理，可以提高监测结果的准确性及可靠性，减少误报和漏报。EWMA若选择较大的权重，可对当前状态进行及时反应；若选择小的权重，可监测系统变化趋势。本研究中权重系数选为0.5。

采用本方法对选定故障类型进行监测，统计量预先进行EWMA处理，监测效果如图4所示。

2) 参数对比。为了更清晰的比较两种降维方法对于监测结果的影响，计算出了两种故障模式下分别采用局部保持投影(locally preserving projection，简称LPP)和LE降维后SVDD监测方法的漏报率和误报率，结果如表2所示。从图表中可以看出，对于具有很强非线性的故障5和故障16，LE降维方法的优势体现在其非线性特征提取之上，LPP算法在非线性数据的处理方面则略有不足。

虽然LE的漏报率偏高，但是误报率远远小于LPP方法。因此，本研究选择LE方法进行非线性降维，提取数据特征。选定的故障类型漏报率及误报率见表3。

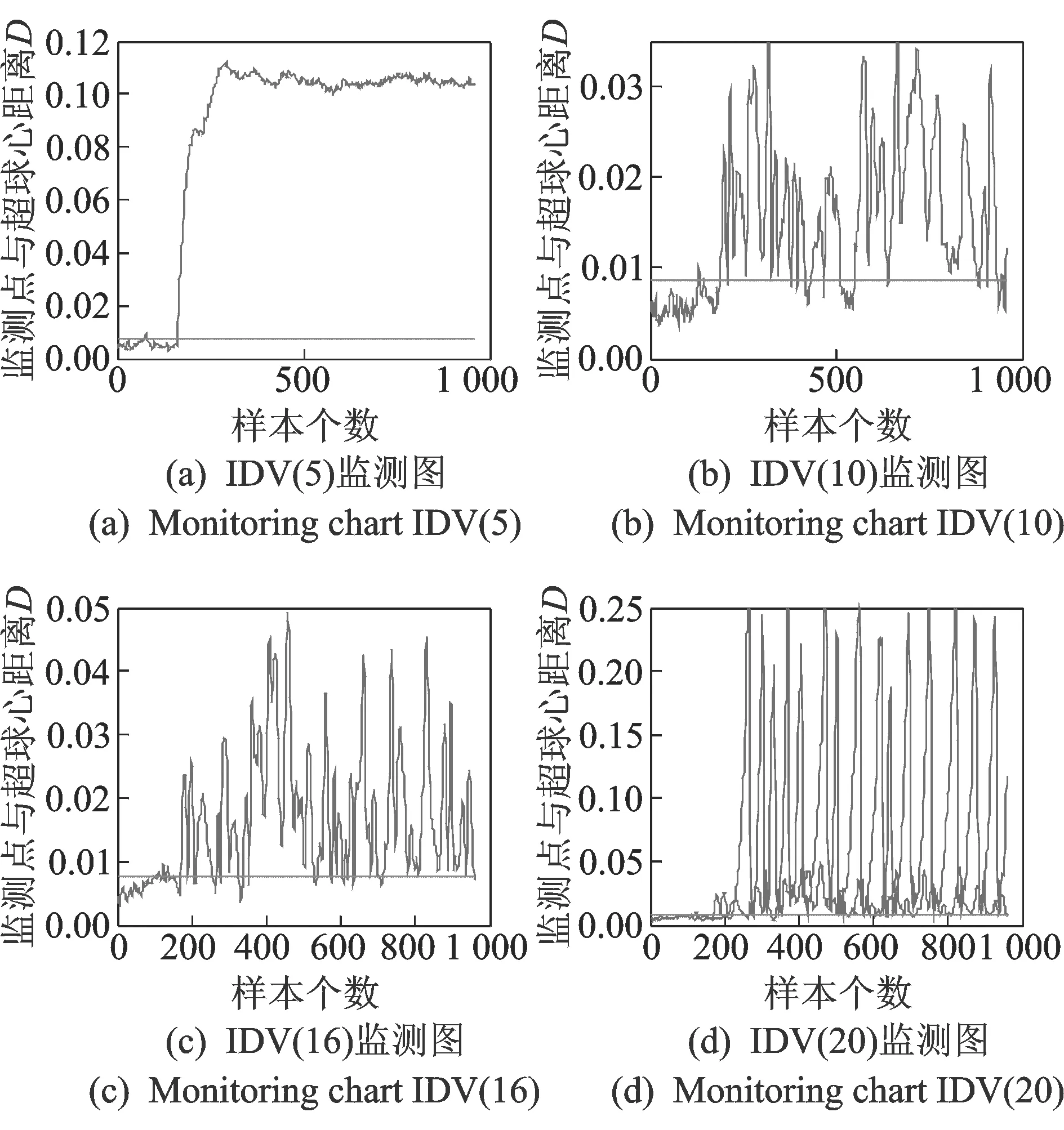
图4 提出方法的监测效果图Fig.4 Proposed method’s monitoring effect picture

Tab.2 Comparisons of monitoring results of LPP and LE dimensionality reduction methods

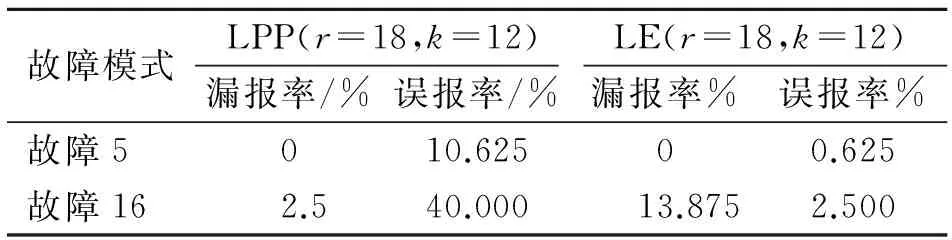
故障模式LPP(r=18,k=12)LE(r=18,k=12)漏报率/%误报率/%漏报率%误报率%故障5010.62500.625故障162.540.00013.8752.500

表3 特征样本LE-SVDD监测结果

根据经验，在复杂机电系统故障监测过程中，如果大部分情况下漏报率和误报率低于10%，则可以得出准确的结果。分析结果可知，对于TE过程几种类型的故障模式，笔者提出的方法的漏报率和误报率均较低，说明该方法具有很好的应用效果。

为了说明所采用方法的适用性，笔者对比了其他异常检测方法在TE过程数据中的结果。文献[14]提到了两种异常数据监测分析方法，即多维主成分分析-支持向量数据描述(multidimensional PCA-SVDD,简称MDPCA-SVDD)和局部切空间算法-特征样本的支持向量数据描述(local tangent space alignment-feature samples SVDD,简称LTSA-FSSVDD)的混合模型。将本研究方法的监测结果与以上两种方法结果进行对比，以漏报率作为评价标准，得到了对比结果如表4所示，其中：Ω为统计量。

表4 TE过程故障监测结果(漏报率)的对比

Tab.4 Comparison of fault monitoring results in TE process (false negative rate) %

文献[15]提出了一种基于集成熵的核主成分分析(integrated entropy kernel principal component analysis,简称IEKPCA)故障监测方法，以误报率和漏报率作为评价指标进行对比，得到对比结果如表5所示。虽然故障IDV(11)的LE-SVDD方法的误报率比IEKPCA方法偏高，但是比重小，不能影响总体的比率。

表5 IEKPCA与LE-SVDD对比结果

以上对比得到的结果均显示了本研究方法在复杂机电系统异常监测上的有限性和优越性，即单独使用SVDD方法具有一定的局限性，漏报率升高，效果不佳。LE方法具有很好的降维能力，降维后通过SVDD进行监测能够得到很好的故障识别效果，并能够显示出识别的优越性。这说明降维和异常点监测方法的组合技术是合理的，能够大大提高故障监测的准确性。

5 结束语

提出了一种基于特征样本的复杂机电系统LE-SVDD状态监测方法。通过在TE仿真过程中进行实验，结果表明该方法在状态监测中具有良好的非线性和高维数据处理能力。同其他方法对比表明，该方法具有一定的优越性。笔者以异常状态监测和故障模式识别方法为基础，研究了系统异常状态监测诊断集成模型构建方法。以调研企业压缩机组系统为研究对象，以生产设备长期运行的集散控制系统的监测数据为基础，根据企业记录的事故案例建立异常案例库，采用LE-SVDD集成方法研究复杂机电系统异常状态监测问题，结果表明组合式异常状态识别方法可以有效监测到系统运行过程中异常事件的发生。

[1] Frank P M. Fault diagnosis in dynamic systems using analytical and knowledge-based redundancy: a survey and some new results[J]. Automatica, 1990, 26(3): 459-474.

[2] Bansal S, Sahoo S, Tiwari R, et al. Multiclass fault diagnosis in gears using support vector machine algorithms based on frequency domain data[J]. Measurement, 2013, 46(9): 3469-3481.

[3] Naimul M K, Riadh K, Imran S A, et al. Covariance-guided one-class support vector machine[J]. Pattern Recognition, 2014, 47(6): 2165-2177.

[4] Diego F F, David M R, Oscar F R, et al. Automatic bearing fault diagnosis based on one-class v-SVM[J]. Computers & Industrial Engineering, 2013, 64(1): 357-365.

[5] Jiang Zhiqiang, Feng Xilan, Feng Xianzhang, et al. A study of SVDD-based algorithm to the fault diagnosis of mechanical equipment system[J]. Physics Procedia，2012, 33: 1068-1073.

[6] Li Guannan, Hua Yunpeng, Chen Huanxin, et al. An improved fault detection method for incipient centrifugal chiller faults using the PCA-R-SVDD algorithm[J]. Energy and Buildings, 2016, 116 (15): 104-113.

[7] Issam B K, Claus W, Mohamed L. Kernel k-means clustering based local support vector domain description fault detection of multimodal processes[J]. Expert Systems with Applications, 2012, 39(2): 2166-2171.

[8] 陈伟，贾庆轩，孙汉旭. 利用小波包和 SVDD的分拣机轴承故障诊断[J]. 振动、测试与诊断，2012，32(5)： 762-766.

Chen Wei，Jia Qingxuan，Sun Hanxu. Bearing fault detection for forting machine using wavelet packet and SVDD[J]. Journal of Vibration，Measurement & Diagnosis，2012，32(5)：762-766. (in Chinese)

[9] 孙文柱，曲建岭，袁涛，等. 基于改进 SVDD 的飞参数据新异检测方法[J]. 仪器仪表学报，2014，35(4)： 932-939.

Sun Wenzhu，Qu Jianling，Yuan Tao， et al. Flight data novelty detection method based on improved SVDD[J]. Chinese Journal of Scientific Instrument, 2014，35(4)：932-939. (in Chinese)

[10]Zhao Yang, Wang Shengwei, Xiao Fu. Pattern recognition-based chillers fault detection method using support vector data description (SVDD)[J]. Applied Energy, 2013, 112: 1041-1048.

[11]Belkin M, Niyogi P. Laplacian eigenmaps for dimensionality reduction and data representation[J]. Neural Computation, 2003, 15(6): 1373-1396.

[12]Tax D M J, Duin R P W. Support vector data description[J]. Machine Learning, 2004, 54(1): 45-66.

[13]Downs J J, Vogel E F. A plant-wide industrial-process control problem[J]. Comuters & Chemical Engineering, 1993,17(3): 245-255.

[14]张少捷，王振雷，钱锋. 基于 LTSA 的 FS-SVDD 方法及其在化工过程监控中的应用[J]. 化工学报，2010, 61(8)：1894-1900.

Zhang Shaojie，Wang Zhenlei，Qian Feng. FS-SVDD based on LTSA and its application to chemical process monitoring[J]. CIESC Journal，2010，61(8)：1894-1900. (in Chinese)

[15]梁银林. 基于集成熵KPCA-SSVM的复杂机电系统状态监测诊断方法研究[D]. 西安：西安交通大学，2014.