灯泡贯流式水轮发电机热流耦合温度场分析

王 亮，王建明，龚海峰，何 涛，陈 柱

(1.重庆理工大学 机械工程学院，重庆 400054；2.重庆水轮机厂有限责任公司，重庆 400054)



灯泡贯流式水轮发电机热流耦合温度场分析

王 亮1，王建明2，龚海峰1，何 涛2，陈 柱2

(1.重庆理工大学 机械工程学院，重庆 400054；2.重庆水轮机厂有限责任公司，重庆 400054)

对型号为SFWG6176-36/3800的灯泡贯流式发电机温度场，运用传热学与流体力学理论，综合考虑温度场、流场的共同作用，进行热流耦合数值仿真研究。通过分析原结构各零部件温度场分布情况，总结了定子线圈存在局部温度过高的原因。对比分析数值计算结果、现场实测数据和热路法计算结果，表明采用热流耦合的数值计算方法是合理可行的。提出的改进措施将定子线圈最大温升降至67.1 K，满足要求，为解决机组的通风散热问题提供方案。

热流耦合；温度场；通风散热；数值分析；灯泡贯流式水轮发电机

水轮发电机温度场问题一直是发电机设计中的难题。自20世纪90年代，许多专家学者就开始利用数值计算方法来解决发电机温度场问题。张大为等[1]利用有限元数值计算方法法对水轮发电机定子最热段温度场进行了计算。张静等[2]研究了大型水轮发电机主要部件表面散热系数的模拟测试及计算方法。孔祥春等[3]采用直三棱柱单元有限元法深入研究了股线绝缘对水轮发电机定子绕组最热段温度的影响。J.Muggiestone等[4]考虑了复杂的电机端部通风系统，提出了端部计算的等效模型，利用有限元法进行了流场和温度场的联合计算。随着近10年来计算机软硬件水平的提高，水轮发电机温度场的数值计算研究已经向多物理场耦合发展。温嘉斌等[5]对大型水轮发电机通风系统以及转子三维温度场进行了综合分析，为该类型电机的热变形及冷却技术研究提供了理论依据。韩力等[6]通过对风路、热路和三维温度场3方面的研究，对大型灯泡贯流式水轮发电机的温升问题进行了全面的计算分析，并利用算例验证了分析和计算方法的有效性。Miao Lijie等[7]为了解决电机中可能出现局部过热和形变的问题，对电机内电磁场、流体场、温度场、变形场进行了综合的分析和研究。

目前，对于大型水轮发电机利用数值分析方法都能得到合理的结果，而中小型灯泡贯流式水轮发电机组空间结构紧凑，发电机布置在灯泡体内，且受水力设计的限制(灯泡体不能过大)，使得径向尺寸较小，轴向尺寸较大，通风条件尤其不佳。另外，灯泡贯流式机型直径小、转速低，转子自身不能产生散热冷却所需要的风压，必须采用外鼓风强迫循环的通风方式。受风路和自身结构影响发电机轴向温度分布不均匀，通风散热问题显得尤为突出。

采用仿真模拟可以在研发阶段提前了解产品性能，进而提出优化方案[8]。本文以型号为SFWG6176-36/3800的灯泡贯流式水轮发电机通风系统为研究对象，借助ANSYS FLUENT数值仿真分析平台，采用热流耦合的数值计算方法，对定子散热冷却问题进行分析计算，结合现场实测数据结果对通风结构提出了局部改进措施。为解决类似机组的通风散热问题提供方案。

1 理论分析

在热源一定的情况下，水轮发电机冷却介质流过电机内部将热源所产生的热量带走，电机内部温度分布的优劣就完全取决于冷却介质的分布[9]。由于发电机是由多种材料零部件组成，它们各自的损耗密度和冷却强度差异较大，因而各部件之间有热交换。在一定时间内，当发电机各部件之间及冷却介质之间的热交换达到平衡时，运行温度就稳定于某一数值。在运行中，发电机各部件发热后的热交换一般是以热传导和热对流的方式进行的。

能量守恒定律表明：流进任意体积单元中的热量等同于流出体积单元的热量加上体积单元中保留的热量，保留的热量导致了体积单元内温度的变化[10]。在守恒定律的基础上结合傅里叶定律可以得到笛卡尔坐标系下的三维稳态热传导微分程[11]：

(1)

式中：λx、λy、λz分别为x、y、z方向上的导热系数；qv为物体单位体积在单位时间内发出的热流量。

对于对流换热问题，在进行数值计算时主要是求解质量连续性方程、动量守恒方程以及能量守恒方程[12]：

质量连续性方程

(2)

动量守恒方程

(3)

能量守恒方程

(4)

式(2)～(4)中：cp为固体比定压热容；ρ为材料密度；λ为材料热传导系数。

1.1 发电机内温度场损耗分析

发电机运行中，所有的损耗几乎都以发热的形式表现出来，其内部的温度场分布主要指定子和转子区域热源的温度分布。定子温度场的热源来自于定子铁芯和定子线圈上产生的损耗，表现为在额定电流时定子线圈的基本铜耗和附加铜耗、空载额定电压时定子轭部和齿部的铁耗、三次谐波在定子齿中引起的附加损耗。转子温度场的热源主要来自于转子磁极线圈的铜耗和以及分布在转子磁极表阻尼绕组中的附加损耗。为得到发电机在运行时定子线圈部位温度数据，定子线圈层间垫条中部埋设有测温元件。

所研究的SFWG6176-36/3800型灯泡贯流式水轮发电机的基本参数和损耗见表1。

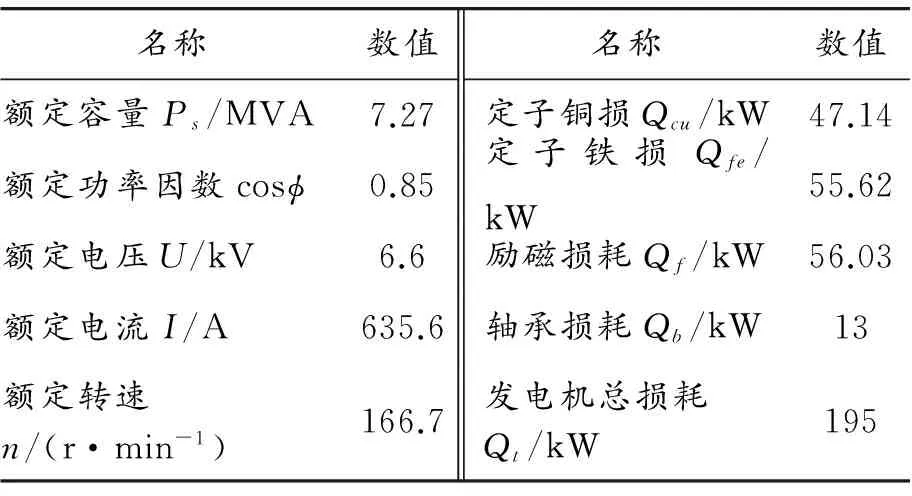
表1 发电机基本参数及损耗

1.2 发电机内流场分析

本文模拟的灯泡贯流式水轮发电机的通风散热系统示意图如图1所示。发电机的额定容量为7.27 MVA，额定转速为166.7 r/min，定子通风系统为铁芯贴壁式密闭强迫循环空气冷却系统。发电机上游端装设有2台混流风机作为通风系统的压力源，冷却发电机的空气从鼓风机的出口流出，进入发电机内部，在电机内不停地进行循环，吹拂发电机发热部分。冷却空气将发电机内的大部分热量带到空气冷却器内与水进行热交换后由冷却水将热量带至发电机外，另一部分热量通过铁芯传导到机座上由机座体表面传导给河水带走。

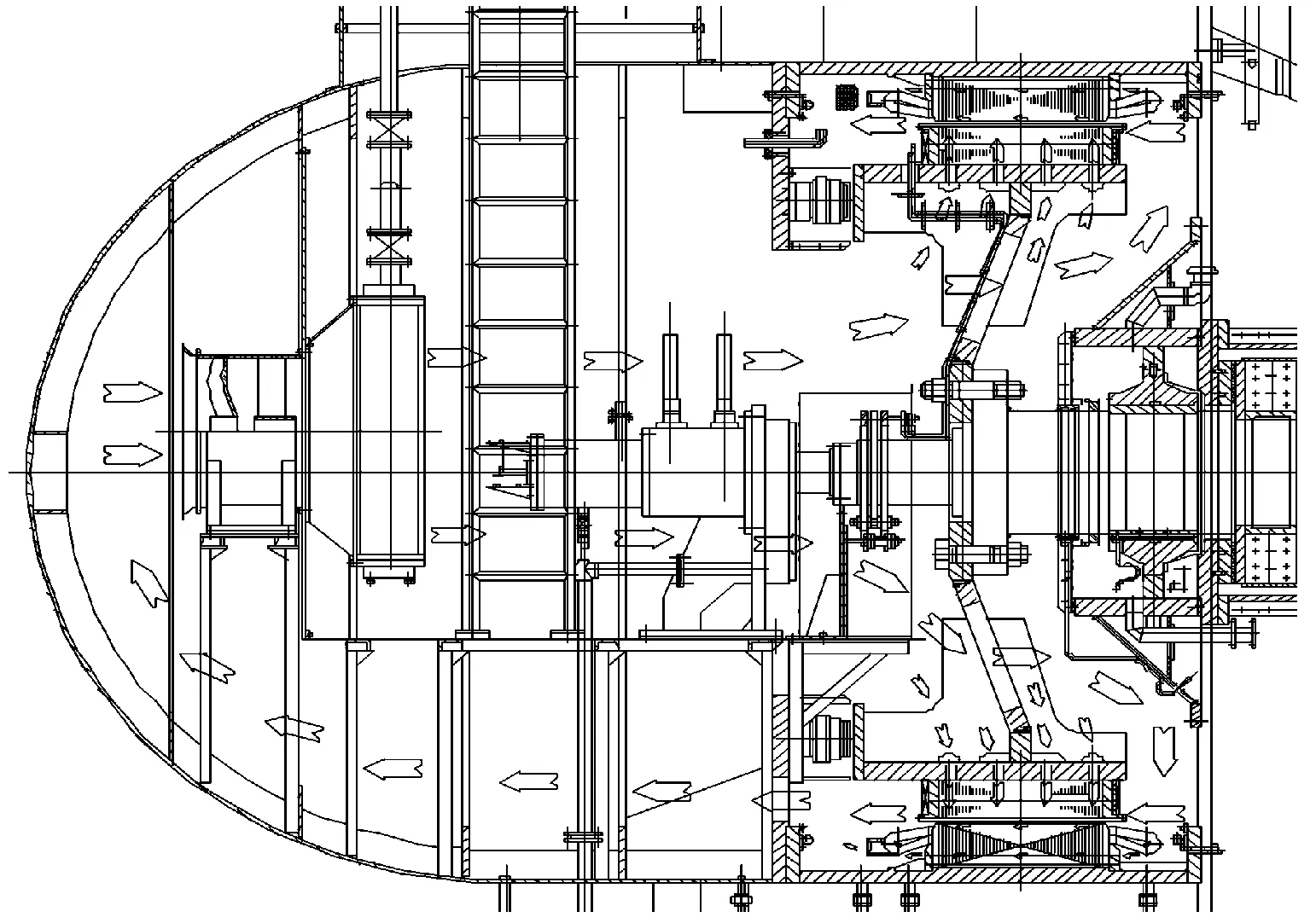
图1 通风散热系统示意图

2 数值分析

2.1 模型的简化

在满足计算精度、确保热流耦合计算能得出合理的数值结果的前提下，对原物理模型做必要简化和假设，主要包括：

1) 由于灯泡贯流式发电机本体具有周期对称性，分析时选取360°/18局部定、转子求解域模型。

2) 定子的发热源自定子铁损和铜损，主要分布在定子铁芯和定子线圈。分析时忽略线圈槽部与端部之间的热交换[13]，定子线圈槽部简化为包裹着一层绝缘层的长方体形状铜芯，不考虑线圈端部的散热。

3) 转子发热主要源于励磁绕组的铜损，主要分布在磁极线圈和极靴的表面处。由于该机组磁极线圈匝间的绝缘平均厚度仅为0.33 mm，故忽略其层间绝缘对散热的影响，建模时转子的磁极线圈结构简化为实心长方体环状结构。

4) 由于定、转子是相对运动的，转子的转动会搅动流体域的运动，故假设以气隙高度的一半划分旋转域和静止域模型。

5) 假设线圈、绝缘、铁芯、导热胶和机座等各零部件之间是紧密接触相连的。

2.2 模型的建立

根据以上模型的简化和假设，在NX三维建模软件中，建立了如图2(a)所示的发电机通风散热的几何模型，其中：定子部分由定子铁芯、定子线圈(含绝缘)、机座等组成；转子部分由磁极线圈、磁极铁芯(含磁极压板)等部件组成。

将几何模型导入ANSYS MESH网格划分模块中。鉴于发电机定转子结构特征较为复杂，采用自适应能力较强的非结构化网格进行单元划分。为了满足计算精度要求，对定子、转子之间的气隙以及线圈、绝缘、导体部分进行网格局部加密处理，最终获得整个通风散热求解域的网格模型，如图2(b)所示。

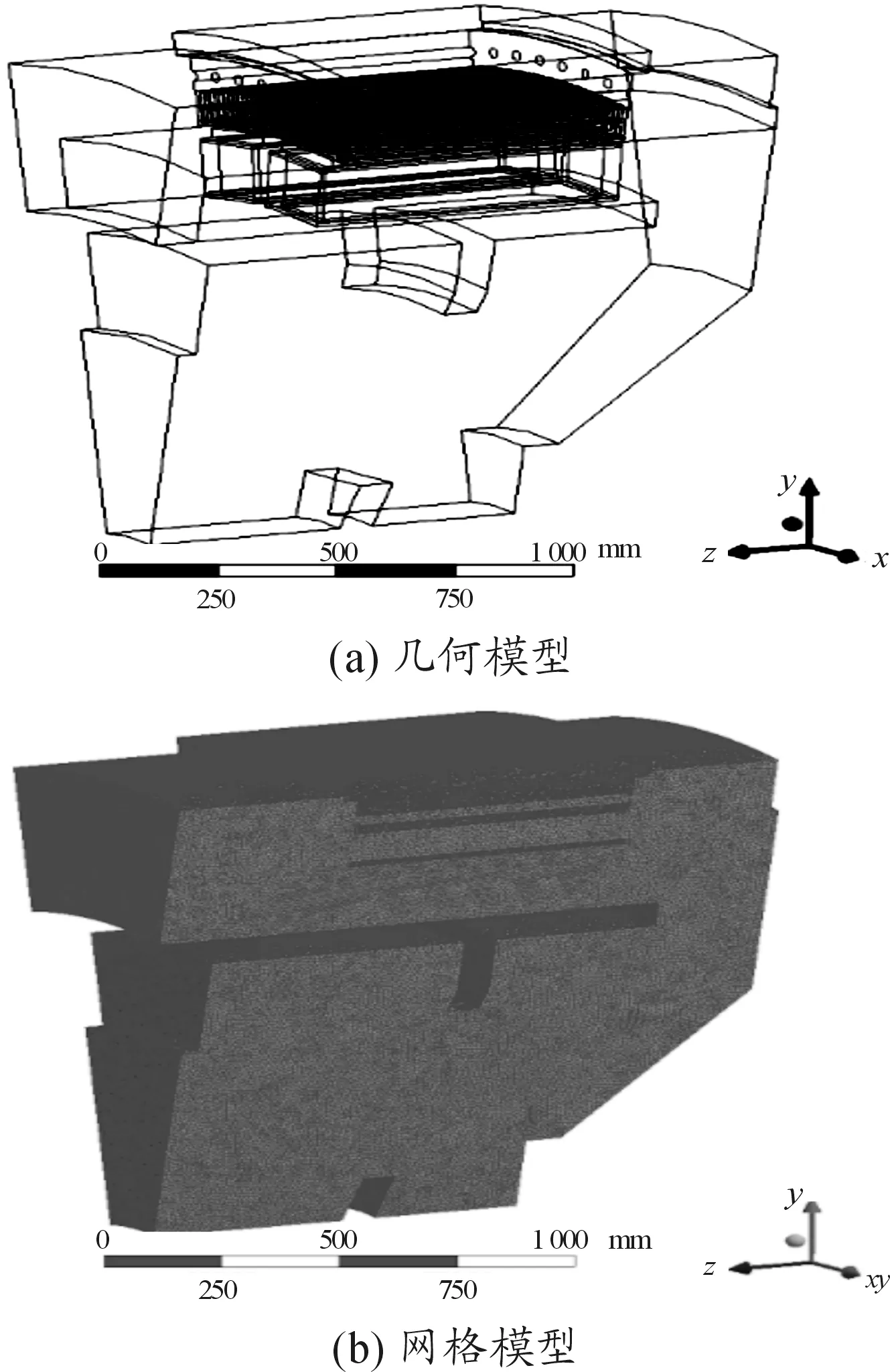
图2 通风散热系统分析模型

2.3 边界条件的设定

根据该发电机的结构特点和仿真模型的建立方法设定边界条件：

1) 发电机转子外圆处在额定工况时最大线速度仅为29.4 m/s，定、转子气隙局部流道内的空气流速也远小于声速，即马赫数很小，故将其作为不可压缩流体来处理。

2) 根据传统计算方法判断流动状态的雷诺数Re=261 226>>4 000，可知空气的流动为湍流流动。

3) 由于发电机定子铁芯为叠片式结构，故铁芯材料的导热系数设置为各向异性，其他部件(见表2)的导热系数按各向同性设置。

4) 旋转域与静止域相连接的边界条件采用interface交界面，对气隙上壁绝对速度设置为0，其他壁面为标准壁面函数。

5) 考虑定子线圈热态电阻的变化，线圈上产生的铜耗由UDF自定义文件给定。

6) 流体域的入口为速度进口，出口为压力出口。

7) 发电机冷却器出风温度为40 ℃，机座外壁水温为30 ℃，环境基准温度为40 ℃。

表2 材料导热系数 W/(m·K)

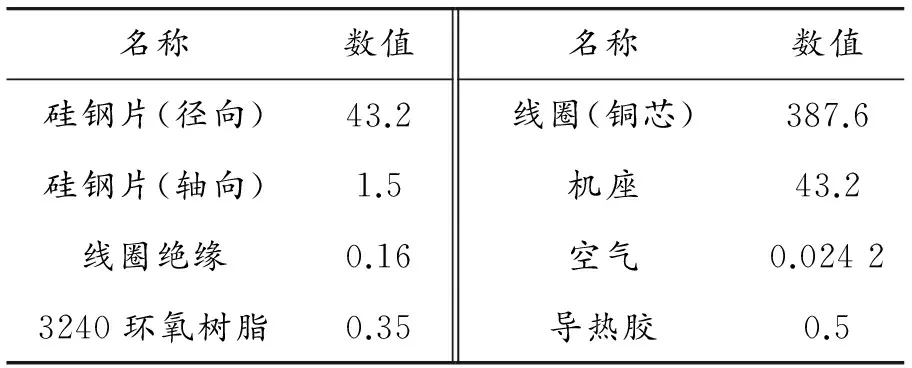
名称数值名称数值硅钢片(径向)43.2线圈(铜芯)387.6硅钢片(轴向)1.5机座43.2线圈绝缘0.16空气0.02423240环氧树脂0.35导热胶0.5

2.4 分析结果

在ANSYS FLUENT分析软件平台上，采用RNGk-ε湍流模型，运用SIMPLEC计算方法，对该灯泡贯流式水轮发电机定转子通风散热系统模型进行热流耦合数值仿真分析，获得空气速度分布，定子铁芯、定子线圈、定子线圈层间垫条中部以及转子线圈的温度场分布，分别如图3、图4所示。

图3 流体域空气速度分布

图3为流体静止域和旋转域风速分布，发电机运行时，其最大速度为36.89 m/s，沿定转子气隙顺时针方向分布。图4所示为原结构温度场分布计算结果：当发电机在额定工况运行时，定子、定子线圈和转子线圈整体沿发电机轴向温度分布不均匀，最高温度出现在发电机上游侧，其中转子线圈最高温升为58.9 K，定子最高温升为69.9 K，定子线圈层间垫条中部测温处的温升最高达95.1 K，温升最高为定子线圈，达到103.3 K，远高于国家标准80 K温升限值。其原因在于原结构定子线圈电流密度过高并且齿部散热不佳，因此必须对原定子结构进行优化改造。

以上数值计算结果与传统热路法计算相比(温升比较数据见表3)，定子铁芯温升最大相差35.9 K，定子线圈温升相差49.7 K，其原因在于：热路法计算结果为平均温升，并不能准确反映温度场的真实分布情况。原结构定子线圈层间垫条数值计算温升与现场实测数据相比仅相差2.7 K，表明分析结果与实测数据基本一致。

3 改进措施

根据定转子温度场的数值计算分析，温升最高处位于定子线圈上游侧，因此在原结构的基础上，仅对定子部分通风系统结构进行局部改造，具体措施如下：

1) 在定子齿部增加5 mm×90 mm矩形轴向通风槽(简称增加轴向通风槽)，每齿布置一个，槽内冷却空气将直接带走定子部分的热量。

2) 原结构定子绕组电密为3.48 A/mm2，高于同类型机组，因此在上述措施的基础上，增加定子线圈的截面积(简称增大线圈截面)，由原线圈截面积507.6 mm2增至593.45 mm2，降低定子线圈截面上的电流密度。

改造后定子处空气速度分布、定子温度场数值计算结果分别如图5、图6所示，主要零部件温升数据见表3，定子线圈层间垫条中部温度数据对比如图7。定子齿部增加轴向通风槽和增大定子线圈截面后，定子线圈最大温升分别为79.9 K和67.1 K，与改造前相比分别降低23.4 K和36.2 K，满足相关技术规范要求，达到预期改造目的。

图5 改造后定子处空气速度分布

图6 改造后定子温度场

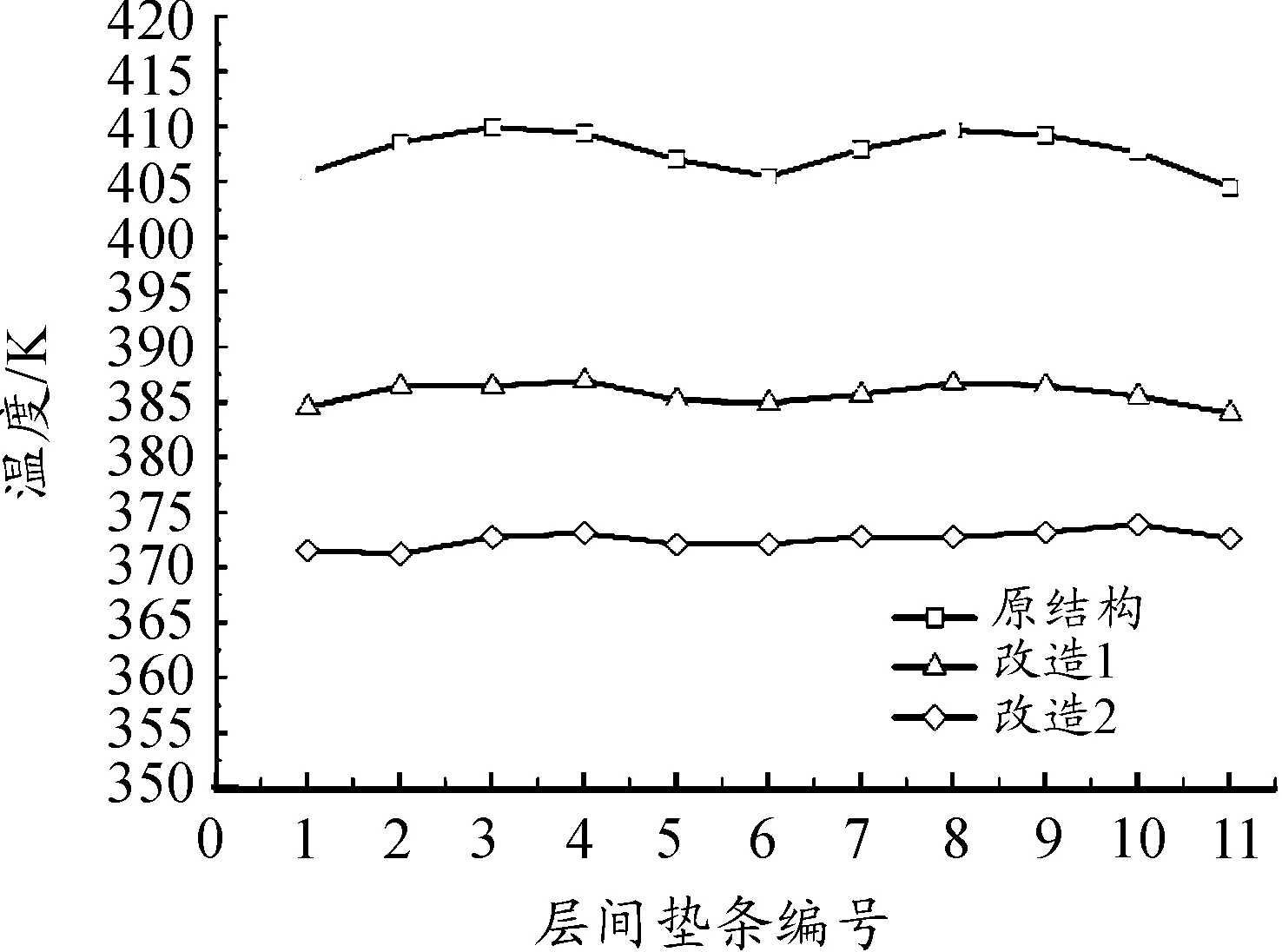
图7 层间垫条中部测温点数据

K

4 结束语

本文对型号为SFWG6176-36/3800的灯泡贯流式水轮发电机定转子温度场进行了热流耦合数值仿真分析，并根据仿真结果对定子通风散热结构提出了两种优化改进方案，将定子线圈最大温升降至67.1 K。仿真结果与现场实测数据的对比分析表明：热流耦合仿真得到的结果与实际测量结果误差仅为3%，在可接受的范围内。仿真结果能较为真实地反映出发电机内部各部件的温度分布，同时能为该类型发电机通风散热系统的设计和改进提供依据。

[1] 张大为,汤蕴璆,迟速,等.大型水轮发电机定子最热段三维温度场的有限元计算[J].电机与控制学报,1992(3):186-194.

[2] 张静,魏永田,刘荣林.大型水轮发电机主要部件表面散热系数的模拟测试与分析[J].电机与控制学报,1994(2):136-145.

[3] 孔祥春，李伟力．股线绝缘对水轮发电机定子绕组最热段温度的影响[J].电机与控制学报,1997(4):228-230.

[4] MUGGIESTONE J，PICKERING S J，LAMPARD D.Prediction of the Heat Transfer From the End Wingding of a TEFC Strip-wound Induction Motor[C]//International Conference on Electric Machines and Drives，IEMD’99.1999:484-486.

[5] 温嘉斌,孟大伟,周美兰,等.大型水轮发电机通风发热场模型研究及通风结构优化计算[J].电工技术学报,2000,15(6):1-4.

[6] 韩力，李辉，马辉，等．大型灯泡贯流式水轮发电机的通风与温升[J]．大电机技术，2000(5)：1-5.[7] MIAO L J，LIU T Y.The Application of FEM in the Physical Field Computation[C]//Proceedings of the Fifth International Conference on Electrical Machines and System，ICEMS2001.Shenyang:[s.n.],2001:1081-1084.

[8] 凌智勇,缪友谊,邢雷杰.电动摩托车控制器的散热性能分析[J].重庆理工大学学报(自然科学),2015(5):1-5.

[9] 熊斌．大型水轮发电机内部流体场和温度场的数值计算[D].哈尔滨：哈尔滨理工大学,2006.

[10]巴纳·萨伯，伊沃·巴布斯卡．有限元元分析的数学建模、校核与验证[M]．北京：航空工业出版社，2013.

[11]宋厚彬．基于多场耦合计算的水轮发电机冷却通风特性分析与优化[D].哈尔滨：哈尔滨理工大学，2014.

[12]朱殿华,郭伟,张雪.水轮发电机通风散热系统的耦合仿真与参数分析[J].水力发电学报,2009,28(4):176-180.

[13]李伟力,宋厚彬,杨逢瑜.水轮发电机通风散热系统多场耦合的数值分析[J].电机与控制学报,2013,17(10):85-90.

(责任编辑 杨文青)

Heat-Fluid Coupling Temperature Distribution Analysis of the Bulb Turbine Generator

WANG Liang1，WANG Jian-ming2，GONG Hai-feng1, HE Tao2，CHEN Zhu2

(1.College of Mechanical Engineering, Chongqing University of Technology, Chongqing 400054, China; 2.Chongqing Water Turbine Works Co.,Ltd., Chongqing 400054, China)

According to the theory of heat transfer and fluid mechanics, considering the joint effect of temperature and fluid-flow field, this study analyzes the temperature distribution of a bulb turbine generator (SFWG6176-36/3800) by using heat-fluid coupling method. By Analyzing the temperature distribution of different parts of the original structure, it finds out the reason why some local temperature of the coil of stator is too high. Comparing the results of numerical analysis, measured data and classical calculation,it finds that the heat-fluid coupling temperature distribution analysis is reasonable and feasible. The proposed improvement is helpful to reduce the temperature rise of the coil of stator to 67.1K, which meets the requirement and provides a scheme for solving ventilation and heat dissipation of other bulb turbine generators.

heat-fluid coupling; temperature distribution; ventilation and heat dissipation; numerical analysis; bulb turbine generator

2016-09-08 基金项目：重庆市自然科学基金资助项目(cstc2015jcyjA90018)

王亮(1990—)，男，硕士研究生，主要从事中小型灯泡贯流式水轮发电机温度场研究，E-mail:myueo@126.com;王建明(1963—)，男，高级工程师，主要从事水轮发电机组产品设计、制造及电站成套技术研究。

王亮，王建明，龚海峰，等.灯泡贯流式水轮发电机热流耦合温度场分析[J].重庆理工大学学报(自然科学)，2017(5):156-161.

format：WANG Liang，WANG Jian-ming，GONG Hai-feng,et al.Heat-Fluid Coupling Temperature Distribution Analysis of the Bulb Turbine Generator[J].Journal of Chongqing University of Technology(Natural Science)，2017(5):156-161.

10.3969/j.issn.1674-8425(z).2017.05.026

TM312

A

1674-8425(2017)05-0156-06