关于k-错位全排列性质的注记
2017-06-29孙玲琍
孙玲琍
(华中农业大学 理学院, 湖北 武汉 430070)
关于k-错位全排列性质的注记
孙玲琍
(华中农业大学 理学院, 湖北 武汉 430070)
探讨k-错位全排列个数的性质,指出已出版教材中关于该性质的错误,并给出正确的证明.
组合数学; 错位全排列;k-错位全排列
MSC 2010:05A15
1 预备知识
定义1[1]对1,2,…,n进行全排列,若每个元素都不在原来的位置,则称为“错位全排列”,记错位全排列的个数为Dn.注:D1=0,D2=1,D3=2.
定理1[1]当n≥2时,Dn=nDn-1+(-1)n.
定义2[1]对1,2,…,n进行全排列,若其中恰好只有k个元素不在原来的位置,则称为“k-错位全排列”,记k-错位全排列的个数为Pn(k).注:Pn(0)=1,Pn(1)=0.




2 主要结果
教材[1]关于k-错位全排列的个数Pn(k)给出了以下性质定理:



但教材[1]对定理6中的(Ⅱ) (Ⅲ) 并没有给出证明,而我们很容易利用n=4进行验证,发现以上两个结论并不成立.
由P4(0)=1,P4(1)=0,利用定理2,可得:
再利用定理1,可得:
从而
因此,本文通过严格证明,修正以上结论如下:


定理6′(Ⅱ) 的证明


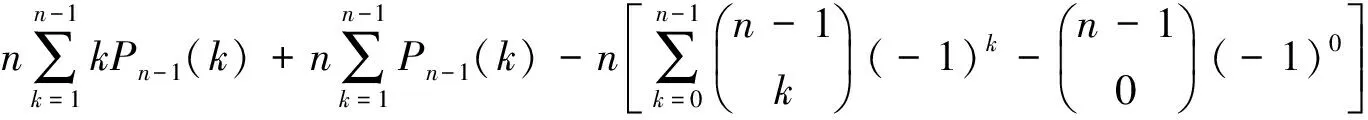


(1)

即
证毕.
定理6′(Ⅲ) 的证明


n(n-1)(1-1)n-2(利用定理4、定理5)=

n(n-1)(n-2)(n-1)!-n(n-1)(n-3)(n-2)!+
n(n-1)[(n-1)!-1]-n(n-1)[(n-2)!-1](利用定理6′(Ⅱ) 、(Ⅰ) )=
(n2-3n+3)n!.
证毕.
利用n=4进行验证:
[1]张秀平.组合数学[M].北京:北京师范大学出版社,2011.
[2]曹汝成.组合数学[M].广州:华南理工大学出版社,2012.
MSC 2010:05A15
[责任编辑 高俊娥]
On the Properties ofk-heterogeneousFullPermutation
SUN Lingli
(College of Science, Huazhong Agricultural University, Wuhan 430070, China)
In this paper, we study the properties ofk-heterogeneousfullpermutation,correcttherelatederrorsinthepublishedtextbookandgivethedetailedproofs.
combinatorics; heterogeneous full permutation;k-heterogeneousfullpermutation
2017-03-18
中央高校基本科研业务费专项资金资助项目(2662017PY091).
孙玲琍,博士,副教授,研究方向:组合数学.E-mail:sunlingli@mail.hzau.edu.cn
O
A
1009-1734(2017)04-0001-04
