棉纱线溶胀动力学模型研究

王方方，徐维敬

(青岛大学纺织服装学院，山东青岛 266071)



棉纱线溶胀动力学模型研究

王方方，徐维敬

(青岛大学纺织服装学院，山东青岛 266071)

为研究棉纱线的溶胀性能，通过显微镜观测记录棉纱线在一定浓度渗透剂的溶液中的动态溶胀过程，对试验数据进行曲线拟合，建立了棉纱线溶胀动力学方程，通过分析论证，二元件开尔文模型可以准确地描述棉纱线在加入渗透剂的水溶液中的溶胀行为，并证明上述所建立的棉纱线溶胀动力学方程是可靠的。

棉纱线 溶胀 动力学 曲线拟合

针织服装向着内衣外穿、高档化、个性化的方向发展，因此对针织物的强力、手感、弹性等提出了更高的要求。棉纬平针织面料作为最常见的针织服装面料之一，为使其更好成为高档外衣面料，要求解决织物布面的平整性。棉纬平针织物在练漂、染色等工艺中易产生褶皱，这不仅受棉纬平针织物自身结构的影响，还与棉针织物在练漂前处理效果有着密切的联系，虽然可以通过防皱整理消除布面的褶皱，但是后整理能源消耗大、污染严重、费用昂贵。棉纬平针织物在练漂液中溶胀对布面平整有很大的影响，所以研究棉纱线溶胀问题对解决棉纬平针织物在染整工艺中易产生褶皱的问题有重大意义，建立合适的棉纱线溶胀模型是研究棉纱线溶胀问题的基础。棉纤维是一种吸水性较高的纤维，它能在多种溶液中吸湿溶胀。在高浓度碱液中，棉织物能够快速溶胀，使织物获得良好的尺寸稳定性，织物强力、延伸性发生一定的变化[1]，在水溶液中棉纱线能发生轻微的溶胀，一定浓度的渗透剂溶液能大大改善棉纱线的溶胀性能。棉纱线从溶胀开始到溶胀平衡的过程称之为溶胀动力学过程。

本文主要通过观察在一定浓度渗透剂的溶液中棉纱线的溶胀行为，建立溶胀动力学方程，并应用模型模拟棉纱线的溶胀，并证明建立的动力学方程的可靠性。

1 试验部分

1.1 试验材料

1.2 试验仪器及方法

1.2.1 试验仪器

LEICA DM2700M型显微镜(德国莱卡)

1.2.2 试验方法

配置不同质量分数的NaOH溶液和一定质量浓度的渗透剂溶液作为溶胀液。

在标准状态的环境中放置棉纱线24小时，然后将纱线均匀的缠绕在载玻片上，将载玻片放在显微镜下，同时在棉纱线上滴1-2滴溶胀液(渗透剂JC-1浓度为2g/L的溶液)，每隔30s用显微镜拍照记录棉纱线的直径变化。

在显微镜图像中的两条棉纱线上选择6个固定的点，用LAS EZ软件测量该纱线直径，然后经过换算比例尺得到棉纱线溶胀前后平均直径。由于棉纤维吸湿横向膨胀大纵向膨胀小[2]，因此可以用棉纱线吸湿溶胀后直径的变化来表示其溶胀的程度即溶胀率

2 试验结果与分析

未溶胀前的棉纱线，经渗透剂处理溶胀30s、60s、90s后的棉纱线，显微镜图像分别如下图1。

图1A、B、C、D分别为棉纱线未溶胀前、溶胀后30s、60s、90s的显微镜图像(50)

测量得到的棉纱线溶胀前后平均直径如下图2所示。

图2 棉纱线直径与溶胀处理时间的关系

棉纱溶胀率随处理时间的变化见表1。

表1 棉纱溶胀率与处理时间的关系

由实验数据绘制时间-溶胀率变化曲线，并用origin软件进行曲线拟合。结果见图3。

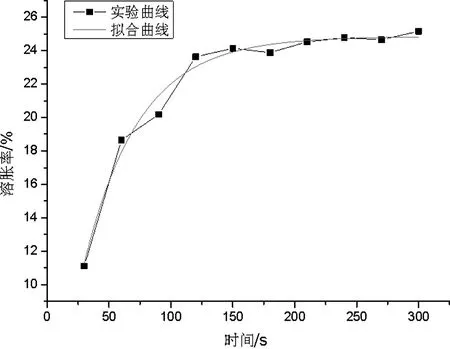
图3 棉纱线溶胀率与处理时间的关系

由图3建立的棉纱线溶胀率随处理时间变化的拟合方程式为：

y=24.83[11.07exp(t/53)]

(1)

该拟合方程R2为0.9808，各指数标准误差不超过5%，所以该方程能够较为准确的反映该试验中棉纱线溶胀率与处理时间的关系。

由长链分子聚集起来的纤维，在受力变形时除了有键长和键角的变化外，还有大分子次价键断裂，导致分子链的逐渐伸展，所以纺织纤维兼有弹性固体和粘性流体的变形特征，也就是具有粘弹性力学性能[3]。对棉纤维而言，其粘弹性力学性能表现为蠕变和应力松弛。

Hearle(1958)提出用缨状原纤理论来解释棉纤维大分子结构，纤维素大分子通过整齐排列形成微原纤，若干微原纤相互组合形成原纤。原纤在不同的位置分裂出来，有的进入棉纤维的无定形区，有的重新进入其他的原纤组织中，连续的缨状原纤形成结晶区。棉纤维在水溶液中发生溶胀，水分子渗入纤维素大分子无定形区，使纤维素大分子体积膨胀，纤维发生溶胀。

当在水溶液中加入适量的渗透剂，加速水分子进入棉纱线芯层，使纤维间充满水，水渗透进入到纤维素无定形区，使纤维素大分子构象发生一定的变化，就相当于纤维受到较小外力时，纤维大分子链段的运动，在这个过程中纤维素无定形区部分氢键断裂，分子链逐渐伸展，纤维分子结构重排，纤维素大分子体积膨胀，整个纤维发生溶胀，这一过程纤维的溶胀变形具有时间效应和时间依赖性。水分子向纤维内部扩散，纤维大分子无定形区部分氢键断裂，在新的位置重排，产生溶胀，纤维形变随时间的缓慢变化，并发生部分不可逆的形变，这相当于粘壶的运动。水分子进入棉纱线纤维间，使纱线溶胀，这一过程中的形变随时间变化，相当于弹簧运动。

三元件模型由一个牛顿粘壶和两个虎克弹簧组成，该模型能够较好的描述纺织品在较小的变形条件下的粘弹性力学性能。三元件模型有两种形式，它们是等效的，我们任选其中一个，如下图4示。

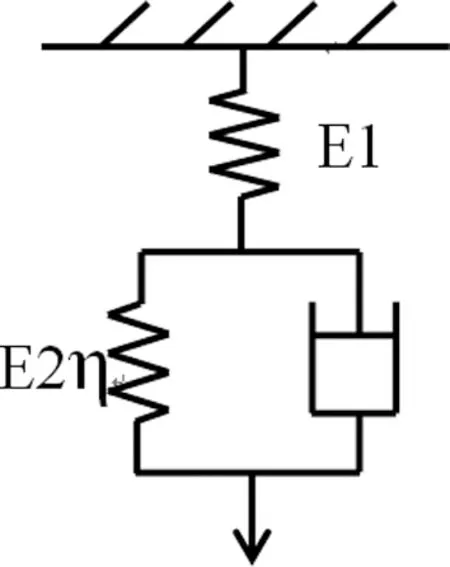
图4 三元件模型

该图中E1，E2分别为弹簧1,2的弹性系数，η为牛顿粘壶的粘滞系数。该模型的的变形特点是弹簧1和弹簧2的变形相等，由此可得其结构关系式如下：

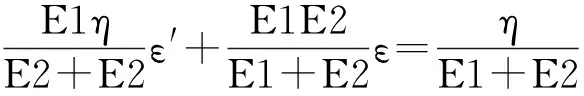
(2)

当б=бc为常数时，其蠕变方程为：

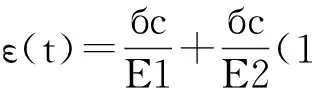
(3)

依据三元件蠕变方程形式，利用origin软件函数添加自定义函数(4)，应用该函数对表1中的实验数据进行曲线拟合，并求得该函数各项参数。

y=бc/E1+бc/E2бc/E2*exp(x/t)

(4)

应用函数(4)对实验数据拟合，结果如下图5所示。

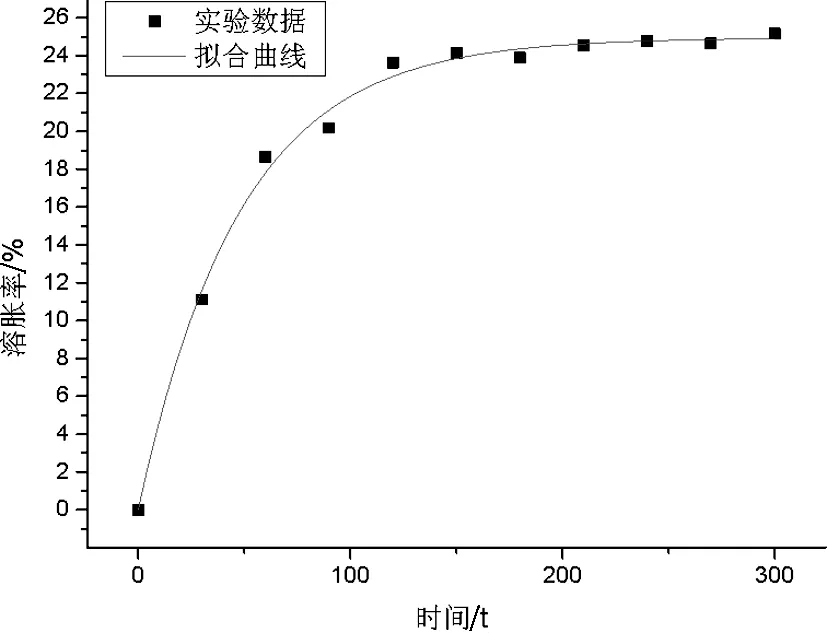
图5 棉纱线溶胀率与处理时间的关系

利用origin求解得到的函数(4)中的各参数值及参数标准误差如下表2。

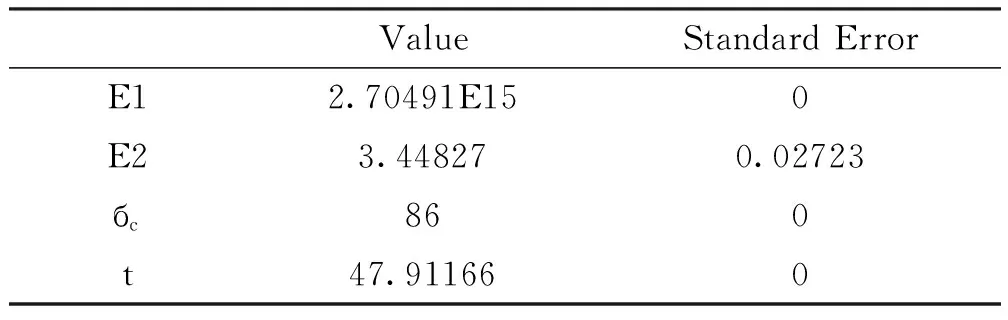
表2 参数值及标准误差值

将表2中的参数带入函数(4)中，得到方程(5)，该拟合方程R2为0.9950，各参数标准误差不超过1，所以该曲线拟合置信度高，参数值合理。

y=3.18E14+24.94(1

(5)

表2中E1，E2分别为三元件模型中弹簧1和弹簧2的弹性系数，水分子在纤维大分子中，纤维间扩散，纤维大分子链运动，相当于受力运动，бc就表示这个力的大小，бc与E2的比值表示该过程中棉纱线的平衡溶胀率，与实验数值吻合度较高。t为推迟时间，即达到平衡溶胀形变63.2%时所需的时间。

可以看出三元件模型中弹簧1与弹簧2的弹性系数相差很大，也就是说在该模型中，相对弹簧2来说，弹簧1完全可以看作刚体；从方程(5)中也可以看出，该方程第一项数值太小，对方程的y值影响可以忽略不计，因此弹簧1可以去掉，也就是在模拟棉纱线溶胀问题中，三元件模型可以简化为二元件开尔文模型。

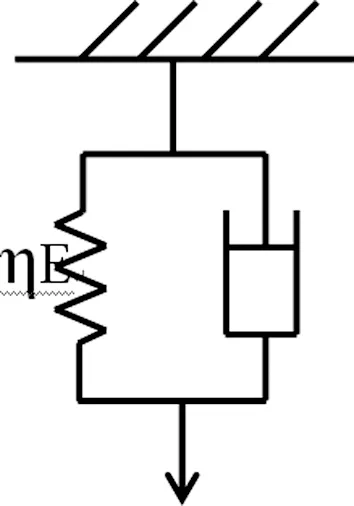
图6 二元件开尔文模型

该模型的结构关系式如下：

(6)

由蠕变变形条件б=бc=常数，初始条件t=0时，ε=0，得到蠕变方程为：

(7)

依据溶胀试验，我们将拟合方程(1)可以简化为以下形式，如式(8)所示。

D(t)=D(∞)[1k*exp(t/τ)]

(8)

D(t)表示棉纱线溶胀率，D(∞)表示纱线达到溶胀平衡时的溶胀率，τ表示棉纱线的溶胀运动的松弛时间，k是系数，由实验误差带来。式(7)与式(8)非常相似，表1中试验所得的棉纱溶胀率在150s到300s时维持在24-25之间，式(8)中D(∞)为24.83，与试验数据非常接近；τ为推迟时间，即形变达到平衡形变值(1)倍所需的时间，由图3中的实验曲线可以估算出，当棉纱线达到平衡溶胀率的63.2%时所需的时间在50s～60s，式(8)中τ值为53s，在实验数据范围内；系数k是一个无限接近于1的数值，主要是由实验误差所造成，也可以理解为一个修正值，式(8)中k值为1.07，在可接受的误差范围内。综上所述，本文建立的棉纱线溶胀动力学方程(1)是合理的、可靠的。

3 结论

通过显微镜观测记录棉纱线吸水溶胀行为，建立棉纱线吸水溶胀动力学方程，并通过对三元件模型的分析，简化为二元件开尔文模型，证明该二元件模型可以准确的描述棉纱线吸水溶胀行为，本文中建立的棉纱线吸水溶胀动力学方程是可靠的。

[1] 闫克璐.染整工艺与原理(上册)[M].中国纺织出版社，2009.

[2] 于伟东.纺织材料学[M].中国纺织出版社.2006.

[3] 于伟东，储才元. 纺织物理[M].东华大学出版社.2009.

[4] 张洪弟，骆成军.三元件模型理论及其在纺织上的应用[J].北京纺织，2004，25(2)：57-59.

Swelling Dynamic Model of Cotton Yarn

WANGFang-fang,XUWei-jing

(College of Textile & Clothing,Qingdao University,Qingdao 266071)

In order to study the swelling property of cotton yarn,the dynamic swelling process of cotton yarn monitored by microscope was recorded,test data was conducted curve fitting and swelling dynamic equation of the cotton yarn was established. The results showed that binary kelvin model could accurately describe the swelling behavior when the cotton yarn was in aqueous solution with penetrant,and it also justified that the established swelling dynamic equation of cotton yarn was reliable.

cotton yarn swelling dynamics curve fitting

2017-02-10

王方方(1991-)，男，硕士研究生，研究方向：纺织工程。

徐维敬(1964-)，男，副教授，硕士生导师。

TS101.92

A

1008-5580(2017)02-0062-04