电能信号降噪研究

庄志惠, 张绪红, 梁远博

(1. 广东技术师范学院 自动化学院， 广东 广州 510665；2. 广东工业大学 实验教学部， 广东 广州 510006)

电能信号降噪研究

庄志惠1, 张绪红1, 梁远博2

(1. 广东技术师范学院 自动化学院， 广东 广州 510665；2. 广东工业大学 实验教学部， 广东 广州 510006)

基于小波信号的变换原理，增加小波重构，提高电信号的精确度，同时增加反馈环节。先对电信号进行小波分解，查看是否有较多的暂态突变，假如有较多的暂态突变，或者电力系统部件有什么故障，可获得实时修正，使最后得到的降噪后信号更加精确。将重构的信号与真实信号相减，得出降噪方式处理后的实验结果发现：强制降噪范围比默认阈值降噪与给定阈值降噪大6～8倍，降噪后的信号与原信号相比差别太大，说明把较多有用信号去除了，这就违背了降噪的初衷，强制降噪后的信号精度不够。在实际工程应用中，可以根据情况选择给定阈值降噪方式以及默认阈值降噪方式。

电能质量；降噪；小波分析

随着大功率电力电子装置的普及应用,电力系统中电能质量问题越加凸显[1-3]。要净化电力环境,解决电能质量问题,就需要准确直观地检测出各类反映电能质量问题的技术数据,但这类技术数据受电磁干扰或检测传感器非线性的影响,往往含有大量的噪声信号[4-8]。去除电能信号中的噪声是更好解决电能质量问题的前提。信号处理是信息科学发展中比较重要的一门学科。信号处理是对信号进行提取、转换、分析、重构等过程的统称,包含信号去噪、特征提取和边沿提取。信号去噪的方法多种多样,传统有线性滤波、非线性滤波及Fourier变换去噪,新发展的有小波变换、小波包分析、EMD分解、高斯滤波、奇异值分解及小波神经网络等[9-11]。

在应用数学的基石上，小波分析方法逐步发展起来，成为一门新的学科，是一种非常好的数学分析工具。近年来，小波分析在电力系统中，特别是暂态信号的处理和分析中的优势越发明显，因此小波分析受到了电力系统分析方面的学者越来越多的关注。本文基于上述背景，设计了电能信号降噪的小波分析方法。

1 小波信号的变换设计

1.1 小波变换

小波变换是信号时频分析和处理的重要理想工具之一，它是延续并且改进了的短时傅里叶变换。因为短时傅里叶变换“时间-频率”窗口不能随频率改变，不具有局部化的特点，导致了灵活性较弱[5]。在对电能信号分解时，它的主要特点是能对时频的局部化分析，在小波变换中，通过伸缩平移运算(即如下式子中a、b值)对电能信号逐步进行多尺度细化，能适应时频域信号分析的要求，并且可以照顾到电信号波形的所有细节，提高电能质量，这是以往用傅里叶变换来分析信号中做不到的。

电信号连续小波变换为：

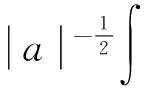
其中:ψ为可选择的母小波；f(t)为信号函数；a为尺度因子；b为平移因子[7]。

根据帕塞瓦尔定理：小波变换中对于确定的小波函数和它的尺度因子以及平移因子，平面坐标内可看成一个矩形的时间-频率窗口，a值决定了时域频域窗口的大小，当a变小时，时间窗口变窄，而频率窗口高度加高；当a变大时，时间窗口加宽，频率窗口高度变低[7]。因此可以观察出信号是在什么时刻变化以及频率大小的变化，体现小波变换局部化特性。

1.2 小波降噪原理

降低信号噪声是小波变换分析在信号处理领域的主要用途之一，电信号降噪可以有效提高电能质量。在电信号的小波降噪中，一个含有噪声的电信号的数学计算模型可以由下式表示：

s(i)=f(i)+σ(i)·e(i),i=(0,1,2,…,n-1)

其中，s(i)为含噪声的电信号，f(i)表示有用信号，e(i)表示混入的噪声信号，σ(i)表示噪声信号的比例系数。

一般情况，噪声存在于有稍高频率的细节中，电信号经过小波分解、阈值处理、最后再进行小波重构之后，提取出有用信号，得到的电信号比以往的方法更接近实际电信号。这是因为通过小波降噪处理以后，更容易地分离出因各种因素夹杂在电信号里面的噪声，而且较之以往的方式，可以体现信号的非平稳特征以及获得信号的相关性。电能信号降噪过程见图1。

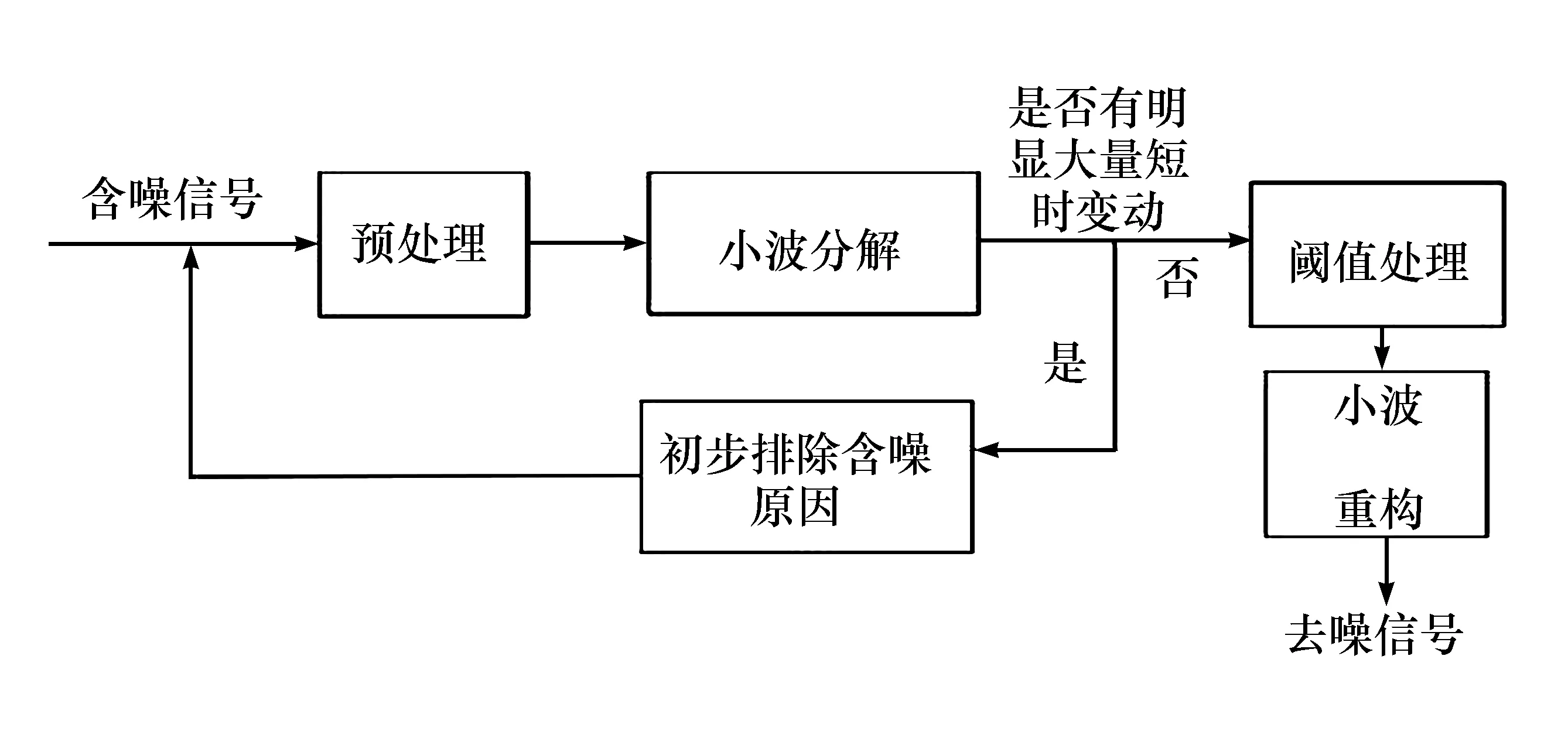
图1 电能信号降噪过程

为了增加小波重构后电信号的精确度，本文增加反馈环节，先对电信号进行小波分解，查看是否有较多的暂态突变，假如有较多的暂态突变，比如电信号暂升、暂降等时，则查看检测时是否错误，或者电力系统部件有什么故障，可获得实时修正，使最后得到的降噪后信号更加精确。

2 实验效果分析

信号突变时，信号的频率也会突变，由于这个特点利用小波变换局部化特性可以检测出某些暂态突变信号的位置，从源头上先排除一些干扰源，比如电信号的暂升、暂降或冲击脉冲等，在小波降噪处理前进行反馈处理，使得小波降噪最终得到的结果更加接近需要的真实信号，也利于分析电信号的特点。以往的检测突变信号的方法，比如傅里叶变换，只能得出信号有哪些频率，即只能知道有突变信号，及大概这些突变信号在什么频段，但是并不能知道突变信号的位置，不利于排除一些干扰源，以含有突变尖峰脉冲信号为例。

图2给出了设计信号的降噪结构，电信号去除噪声的过程一共有3个步：第一，将含有噪声的电信号进行小波变换，选择一个合适的小波并确定分解的层数，再进行小波分解的计算；第二，将小波分解高频系数进行阈值的量化处理，阈值处理共有3种方式，即改进阈值处理、软阈值处理和硬阈值处理，下文将进行对比；第三，将电信号进行小波重构，将小波分解后的低层的低频系数以及高层的高频系数进行小波重构。决定电信号降噪的质量的取决于第二步，选择阈值以及阈值量化处理对小波降噪进行改进。

使用正弦波信号，并在信号中加入高斯白噪，结果见图3。降噪后的波形基本还原了原始波形，并且基本消除了信号中的噪声。

为了真实反映降噪后信号与原信号的差异，将重构的信号与真实信号相减，得出三种降噪方式处理后的重构信号与原信号的差值见图3，从纵轴的范围大小可以看出，对比3种降噪方式，改进的阈值处理纵轴的范围比硬阈值降噪和软阈值降噪大6～8倍，降噪后的信号与原信号相比差别太大，说明把较多有用信号去除了，这就违背了降噪的初衷，改进的阈值处理后的信号精度不够，在实际工程应用中，可以根据情况选择硬阈值降噪和软阈值降噪方式。

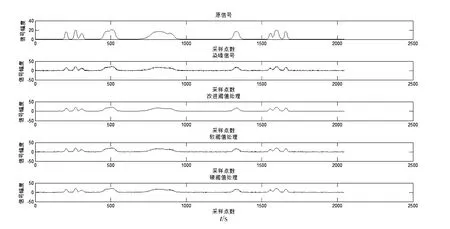
图2 信号的降噪结构

图3 改进后拟合结果

3 结论

综上所述，通过对比FFT与小波变换处理正弦信号，小波变换具有明显的优势，即有很好的反馈效果，可以在电信号降噪前对信号进行处理，使得最后得到的信号还原度高。比较了集中阈值处理方式，分析出比较好的阈值处理方式，也说明了小波降噪的确可以应用于工程实践。

References)

[1] 范媛媛,桑英军,胡光,等.基于小波变换的电能质量监测[J].沈阳工业大学学报,2014(6):681-687.

[2] 林琳,杨金成,张卫辉,等.基于S变换与全局最优阈值的暂态扰动信号降噪[J].电测与仪表,2015,52(23):48-51.

[3] 陈茜,马永杰. 基于小波分析的电能扰动研究[J].大电机技术,2015(5):7-10.

[4] 宋平岗,文发.基于LMS形态滤波和Hilbert变换的电能质量扰动定位[J].华东交通大学学报,2015(1):86-92.

[5] 王燕,李群湛,高洁,等.电能质量扰动信号的自适应去噪方法[J].电力系统自动化,2016,40(23):109-117.

[6] 姜鸿羽,马宏忠,姜宁,等.变电站噪声智能预测及其主动控制[J].电工电能新技术,2014(9):74-80.

[7] 陈晓娟,王文婷,李楠,等.小波熵自适应阈值的电能质量信号去噪新方法[J].电测与仪表,2014(15):68-73.

[8] 杨蒙薇,陈晓英,贾书文,等.基于零空间追踪算法的电压波动与闪变检测方法的研究[J].中国电力教育,2014(33):212-214.

[9] 赵宏飞,马宏忠,陈楷,等.用于变电站噪声有源控制的一种算法研究[J].电工电能新技术,2014,33(10):70-75.

[10] 杨挺,尚昆,袁博,等.基于压缩感知的盲源信号分离检测方法[J].天津大学学报,2016,49(11):1138-1143.

[11] 郝晓弘,魏莹.基于改进EEMD的电能质量扰动检测研究[J].电子设计工程,2017,25(2):88-92.

Research on noise reduction of electric energy signal

Zhuang Zhihui1, Zhang Xuhong1, Liang Yuanbo2

(1. School of Automation, Guangdong Polytechnic Normal University, Guangzhou 510665, China；2. Experimental Teaching Department, Guangdong University of Technology, Guangzhou 510006, China)

Based on the transformation principle of the wavelet signal, the wavelet reconstruction is increased and the accuracy of the electrical signal is improved. At the same time, by increasing the feedback links, the wavelet decomposition is carried out on the electrical signal to see if there are more transient mutations. If so, or there are some faults in the components of the power system, the real-time correction is completed, which can make the final noise-reduced signal more accurate. By subtracting the reconstructed signal from the real one, the experimental results show that the forced noise reduction range is 6-8 times bigger than that of the tacitly approved noise-reduced threshold and the given noise-reduced threshold. The noise-reduced signal is greatly different from the original one, indicating that more useful signals are removed, which is against the original intention for the noise reduction, and the forced noise-reduced signal is not accurate enough. In practical engineering application, the given noise-reduced threshold method and the tacitly approved noise-reduced threshold method can be selected according to the real situation.

quality of electric energy; noise reduction; wavelet analysis

10.16791/j.cnki.sjg.2017.06.018

2016-12-13 修改日期：2017-02-24

广东省自然科学基金项目“超导限流器与电力系统继电保护配合的研究”(S2013010015007)

庄志惠(1980—)，男，广东揭西，硕士，实验师，主要从事计算机控制技术和电气新技术研究.

TM76

A

1002-4956(2017)06-0074-03