铁路货物快运服务网络鲁棒性优化方案

刘欣萌

(西安航空学院经济管理学院，陕西 西安 710077)



【交通运输】

铁路货物快运服务网络鲁棒性优化方案

刘欣萌

(西安航空学院经济管理学院，陕西 西安 710077)

针对计划期间货运需求的波动情况，构建了铁路货物快运服务网络设计鲁棒优化模型。通过对比传统铁路货物快运服务网络设计基础模型，以总运输成本最小为目标，决策内容隐含车流的中转方案和摘挂方案、列车编组计划、运到期限等运输服务约束，采用和声搜索算法对模型求解，循环迭代至获取较优结果。研究结果表明，鲁棒优化模型对运输需求变动的适应性较强，且运到期限增大，总成本减少。

货物快运；列车服务网络设计；鲁棒性；和声搜索

我国铁路的货运组织改革，对货物运输提出了更高的要求。社会物资品类和结构的细化，又进一步增加和诱发了新的货运需求[1]。铁路货物快运是铁路货运产品中以运输高附加值货物为主的货物运输方案，向货主承诺货物运到时间，具有安全、快速、准时、便捷等特点，体现快捷和限时送达等优势。如何开展货物快运列车服务网络优化设计，使货物列车更好地适应市场发展，满足货主需求，同时降低运输成本、提高运输收益，已成为该领域亟待解决的问题[2]。

运输服务网络通常是指在物理网络的基础上，由节点和联弧组成[3]，运输主体通过决策确定的运输服务方案，具体包括车流径路、场站节点、服务频率等。国内外学者对此进行了深入的研究，例如在服务网络研究方面， Maia等[4]针对多通道网络货运业务，以普通货运和公铁联运为例，提出了一种创新的分配模型。Bai等[5]设计的随机服务网络，主要解决不确定因素对目标函数的影响，提出了一个新的随机货运服务网络设计模型与车辆路径选择方法，主要增强了模型的灵活性。Hajiaghaei-Keshteli等[6]针对铁路运输的综合调度问题进行算法对比，模型以总成本最小为目标，得出Keshtel算法(KA)相比于遗传算法(GA)应用于铁路综合调度问题具有更好的求解效果的结论。刘杰等[7]采用节点拆分的方式构建了既有繁忙干线货运产品网络。

服务网络的研究给规划者提供了规划依据，可是在实际运输中，运输需求会因季节、周期、天气、政策等各种因素导致运输中发生不可控的情况。针对不确定因素的研究，比较成熟的方法是鲁棒模型[8]，该方法强调的是在优化开始时就考虑模型的不确定性，使优化的结果达到对不确定因素不敏感及性能指标最优的统一，可以有效解决众多行业对不确定优化问题的需求，因此考虑鲁棒性以后的结果被认为是更稳定的，而相对其他模型却不一定是值最优的。对于鲁棒性的研究， Najafi等[9]针对自然灾害的应急预案，提出了在地震发生后救援物资的输送方案。定义救助条件为不确定的，即需求和供给是不确定的，建立了多目标鲁棒优化模型。李婷婷等[10]考虑城镇化发展阶段客运需求的不确定性，构建了基于有能力限制的层级选址模型和遗憾鲁棒优化模型。

长期以来铁路运输需求很难准确预知，也容易受各种因素的影响，给铁路货物快运服务网络设计带来了诸多不确定的条件。因此，构建多场景需求变动下货物快运服务网络设计的鲁棒优化模型，可以有效解决目前铁路货物快运过程中面临的问题，对提高经营质量和效益，适应市场、扩大市场，实现可持续发展都具有深远的意义。现阶段鲁棒性在服务网络设计中的应用尚处于空白，本文借鉴鲁棒性在枢纽选址[11]、中转班列开行方案[12]等方面的应用，建立了货物快运服务网络设计鲁棒优化模型，最后采用和声搜索算法对模型进行求解。

1 铁路货物快运服务网络设计鲁棒模型的分析

铁路货物快运服务网络模型，其核心是确定候选车流集，根据运输需求、通道能力，运输时限等，确定开行方案、开行频度、运行路径。对所有车流合理合并，可以有效压缩网络规模，提高运输效率。在此基础上，考虑到实际货运量和计划货运量间存在偏差，会影响基础模型最终设计的结果，使得所求结果的抗干扰性较差，因此，本文提出了铁路货物快运服务网络设计鲁棒优化模型(简称鲁棒优化模型)。

在鲁棒优化模型中，鲁棒优化理论中的不确定因素通常对应离散的场景(scenario)或连续的区间范围[13]，最优解可以使得所有的确定性参数的稳定性最高，从而实现鲁棒优化模型的抗干扰性。本文的鲁棒优化模型中，选择场景来表示不同时段的货运需求量。鲁棒优化模型的决策思路流程图如图1所示。

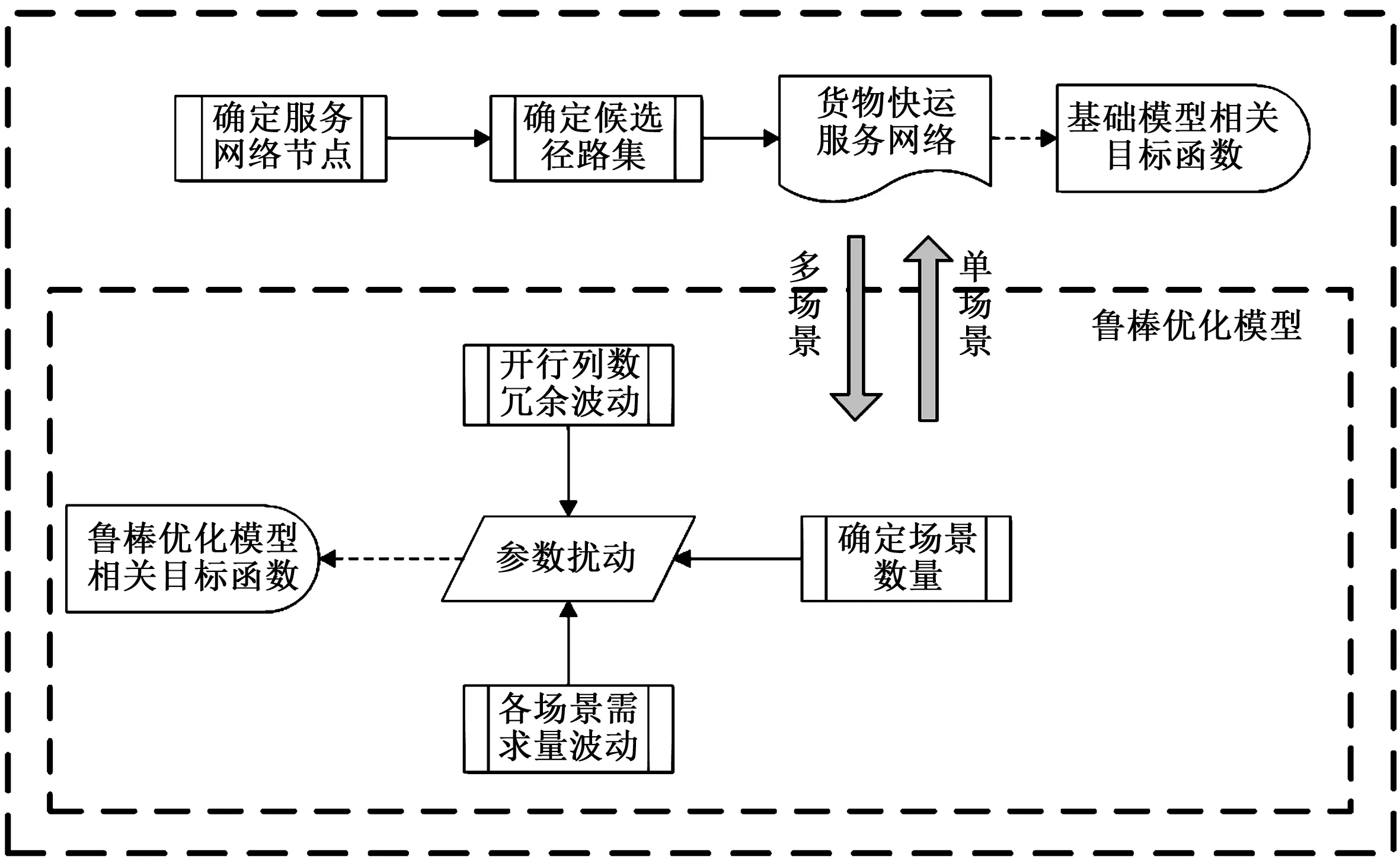
图1 铁路货物快运服务网络模型决策思路流程图Fig.1 Decision flow chart of railway freight transportation service network model

1.1 确定车流径路的候选车流集

车流径路是求解货物快运服务网络设计的核心要素[14]，对于货物快运服务网络设计而言，为货流确定可行路径(即车流径路)，将货流分配在其所在路径上，是编组的首要任务。因此，考虑到实际情况，运输企业总成本最小，车流需要和其他车流合并运行至终点。提前定义好供流量分配时选择的候选径路集，可以提高每个车流的选择速度。由于货物快运通常是干线运输，其运行路径规定为特定路径，在这里视为已知。

1.2 建模思路

考虑多场景条件下鲁棒优化问题的优化模型的一般形式[15]：

minZ=Z1(X)+Z2(X,S) s.t.X∈Ω ,

(1)

其中

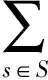
(2)

2 铁路货物快运服务网络设计鲁棒模型的建模与求解

2.1 符号定义

(1)集合

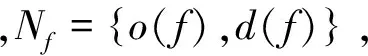
(2)参量

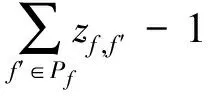
(3)决策变量

xf为0-1变量，车流f是否开车，若是则xf=1，否则xf=0。yf为整数变量，表示车流f所开行铁路货物快运班列的列数。zf,f′为0-1变量，车流f是否并入f′，若并入zf,f′=1，否则zf,f′=0。yf,s为整数变量，表示场景s下，车流f所开行铁路货物快运班列的列数。

2.2 模型构建

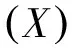
(3)

除此以外还需要考虑服务网络在各个场景下的偏离程度，偏离程度会存在正偏离和负偏离两种情况，因此在求解的过程中需要取绝对值处理，所以总偏离程度可以理解成是开行列数的波动导致固定成本的变动数额。具体表示为：

(4)

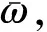
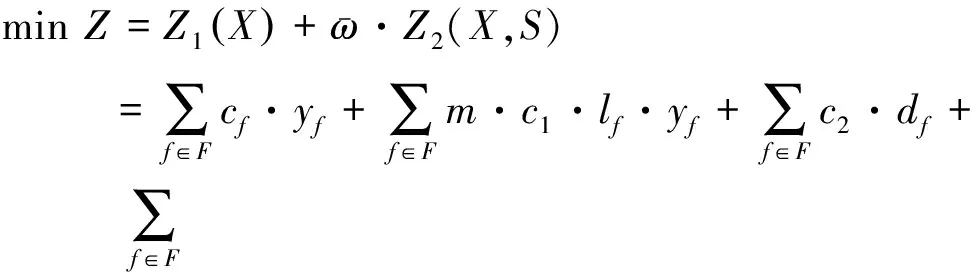
(5)

约束条件如下：

xf+zf,f′≤1 , ∀f∈F,f′∈Pf,

(6)

zf,f′≤xf′ , ∀f∈F,f′∈Pf,

(7)

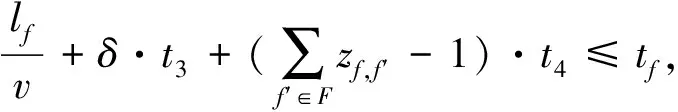
(8)

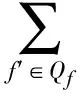
(9)

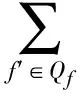
(10)

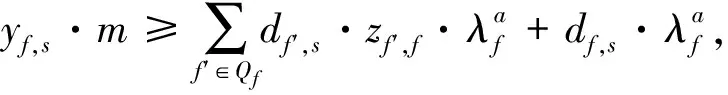
(11)

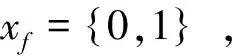
(12)

yf∈N+, ∀f∈F ,

(13)

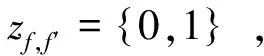
(14)

yf,s∈N+, ∀f∈F,s∈S 。

(15)

式(6)为车流合并约束，对于任意一条车流，或者自行开车，或者并入其他车流；(7)为并入条件约束，被并入的车流必须开车且是并入车流的候选径路集；(8)为运到期限约束，运输时间和途中作业时间的总和应小于等于运到期限；(9～10)为开行列车数冗余范围约束，开行的班列数大于需求的最小值，小于需求的最大值；(11)为各个场景下的运能约束：任意路段上的流量之和不超过服务区段的最大编成辆数；(12～15)为变量取值约束。

由于铁路货物列车的开行方案是比较长远期的规划，因此在优化开行方案的过程中考虑计划期内各个场景(阶段)的预测货运量更具有实用价值。

3 求解算法

货物快运服务网络设计鲁棒优化模型为整数规划模型，智能优化中的和声搜索算法在求解大规模复杂问题中具有适应度强、编码简单、类比清晰、步骤明确等优势[16]。本文采用该算法进行求解。具体步骤如下：

Step 1 和声编码

货物快运服务网络设计鲁棒优化模型的编码和决策变量相关。每个和声的编码形式如下：

(17)

Step 2 生成初始解和初始化和声记忆库

根据以上分析，和声记忆库(HM)有保存初始可行解和在迭代过程中获得较优解的作用。而初始化和声记忆库，需要求得初始可行解，由于路网的复杂性，且约束条件较多，使得求解难度增大，可能产生较多不可行解，对求解效果产生影响。因此,本文给出了两阶段的可行解的生成办法，可以较好地得到初始可行解，如图2所示。

Step 3 生成新的和声

进行音调微调操作后，多场景需求变动下铁路货物快运服务网络设计的鲁棒优化模型需要检验结果是否满足约束条件，如满足则进行下一步操作，如不满足则按照可行解的生成办法重新生成新和声。

Step 4 更新和声记忆库

利用式(5)对模型生成的新解进行评估，如果其评估结果好于和声记忆库中最差的可行解，那么就将新生成的解更新至和声记忆库中。

Step 5 算法终止条件

不断更新和声记忆库中的可行解与最优目标函数，直到迭代次数达到规定的最大迭代次数，则算法终止，认为此时算法已经收敛到最优，并输出最优解与最优函数值。

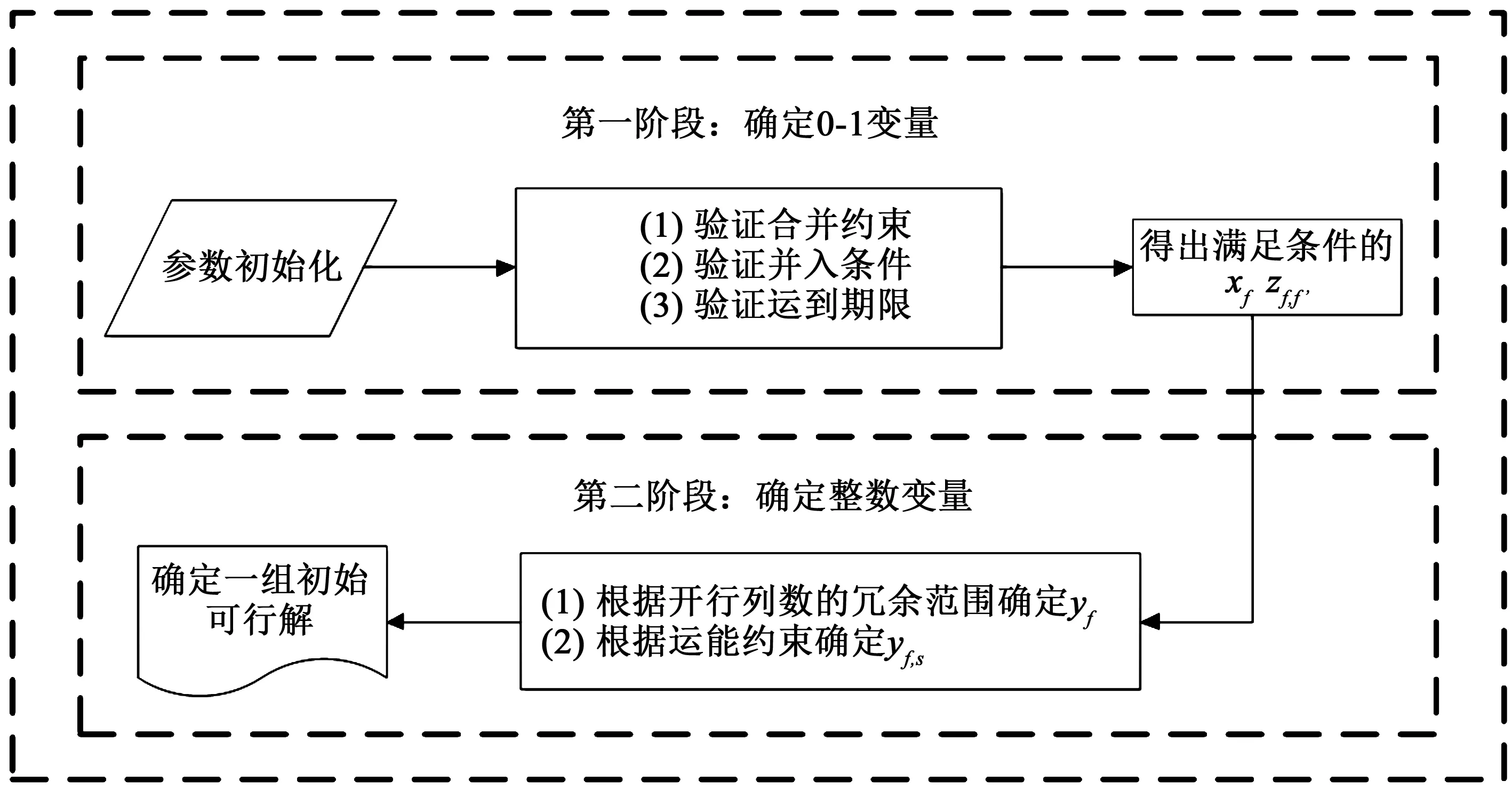
图2 初始可行解生成示意图Fig.2 Schematic diagram of initial feasible solution

图3给出了和声搜索算法流程图。

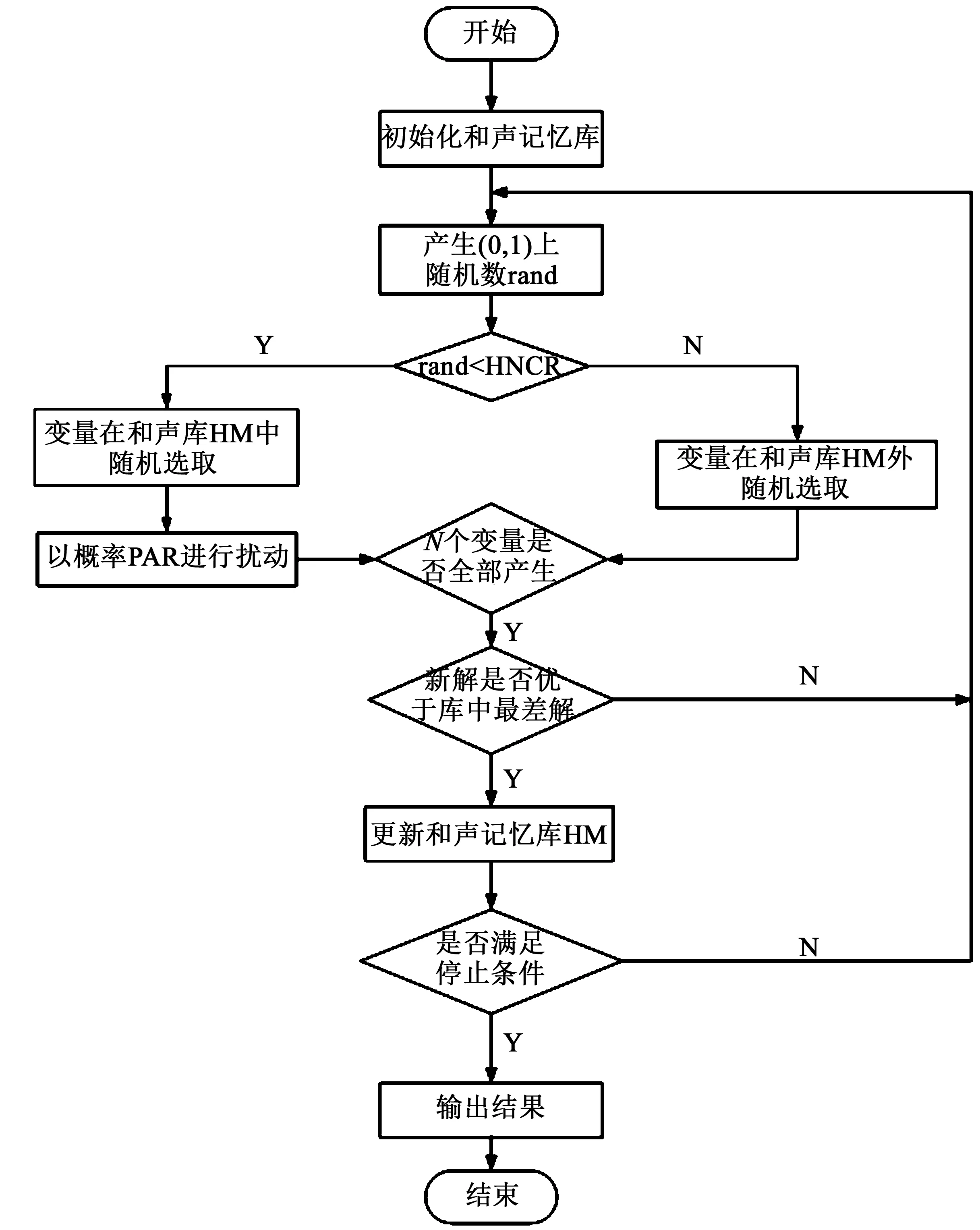
图3 和声搜索算法流程图Fig.3 Flow chart of harmony search algorithm

3 算例分析

为验证求解结果的准确性和可行性，使用算例进行分析。构建服务网络结构，所有节点间均可以双向服务，铁路运输网结构如图4所示。节点间OD需求量和固定成本见表1，各参量取值见表2。

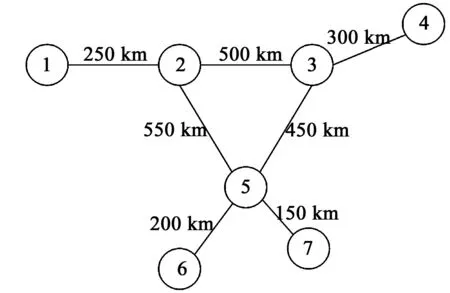
图4 铁路运输网结构图Fig.4 Railway transport network structure diagram

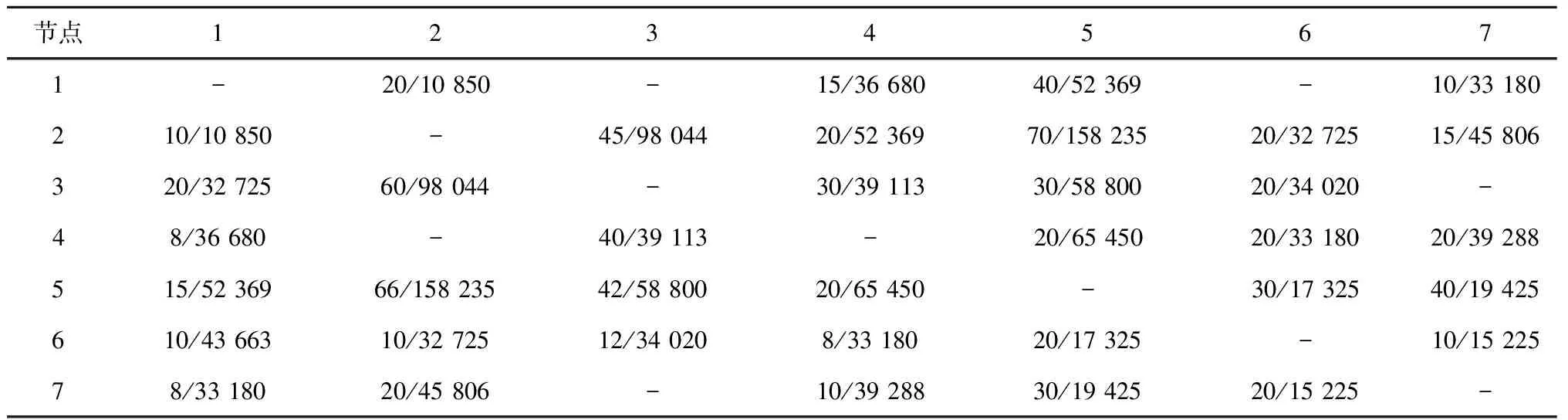
节点12345671-20/10850-15/3668040/52369-10/33180210/10850-45/9804420/5236970/15823520/3272515/45806320/3272560/98044-30/3911330/5880020/34020-48/36680-40/39113-20/6545020/3318020/39288515/5236966/15823542/5880020/65450-30/1732540/19425610/4366310/3272512/340208/3318020/17325-10/1522578/3318020/45806-10/3928830/1942520/15225-

注：以上数据满足递远递减规律，参考运行线始末站间的距离、成本车辆使用费用以及租用运行线的费用等进行估算。

表2 各参量取值

注：以上数据依据铁路货物快运的统计值和运输付费清算标准，以及参考文献[10-11]中对于参数取值的情况等进行估值。

采用和声搜索算法对模型求解，算法由C#语言在Visual Studio 2010平台下实现，在Inter(R)Core(TM)i5-3210M CPU和2 GB内存环境下运行。和声记忆库大小取80，记忆库取值概率取值在0.9，微调概率0.3，经过测试，取最大迭代次数为4 500，场景数选择12个。为了对比运到期限对模型的影响，选择运到期限1取值13.8 h，运到期限2取值9.9 h。

经过多次计算，在运到期限1时，经过3 106次收敛，收敛值为27 121 152元，也就是总成本和总偏离程度的加权值，其中总成本5 806 423元，总偏离程度21 314 729元；运到期限2时，经过3 781次迭代收敛，收敛值为29 181 330元，其中总成本5 452 476元，总偏离程度23 728 854元。平均运行时间125 s。收敛图如图5所示。

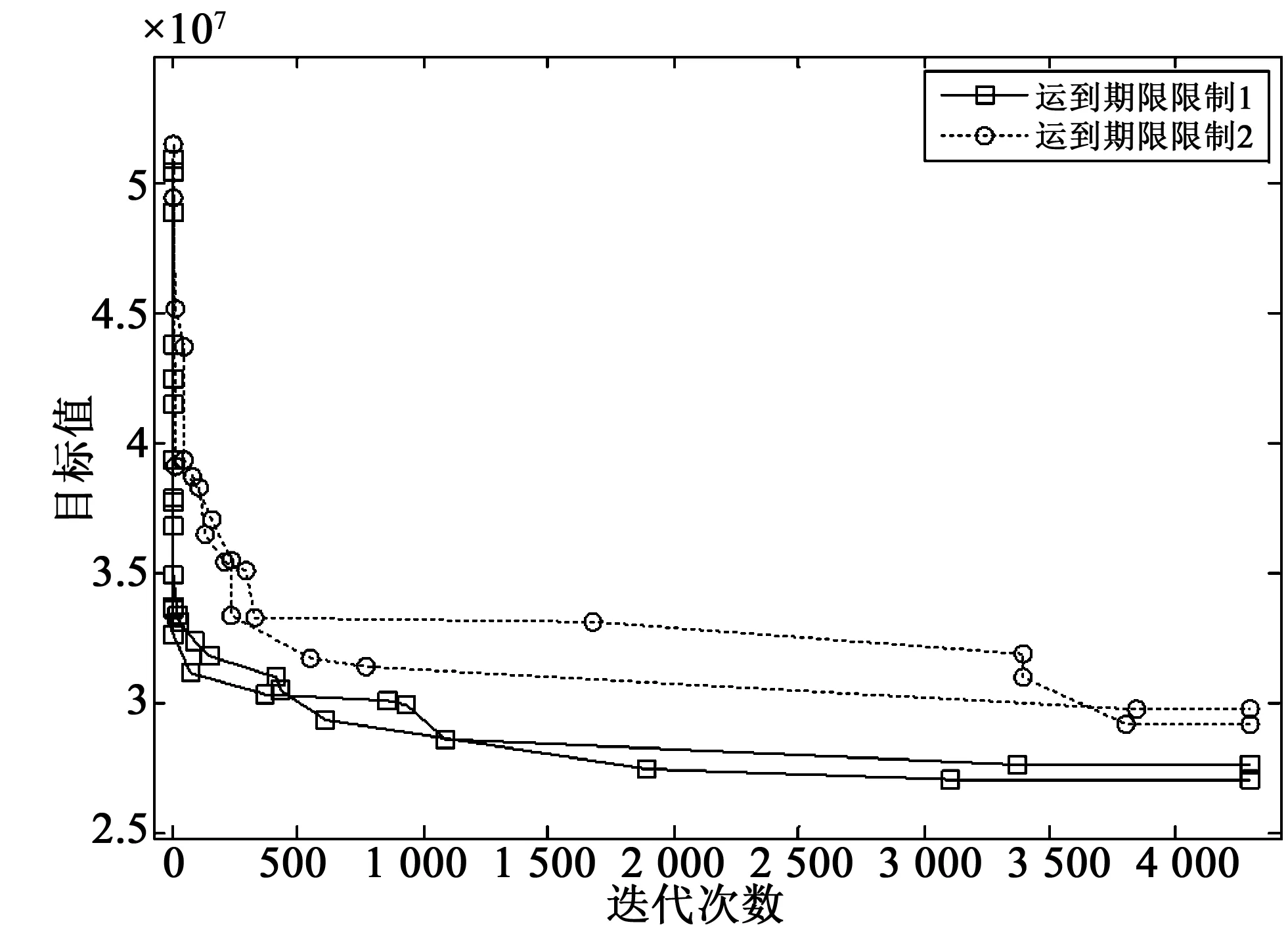
图5 和声搜索算法收敛过程示意图Fig.5 Convergence process of harmony search algorithm

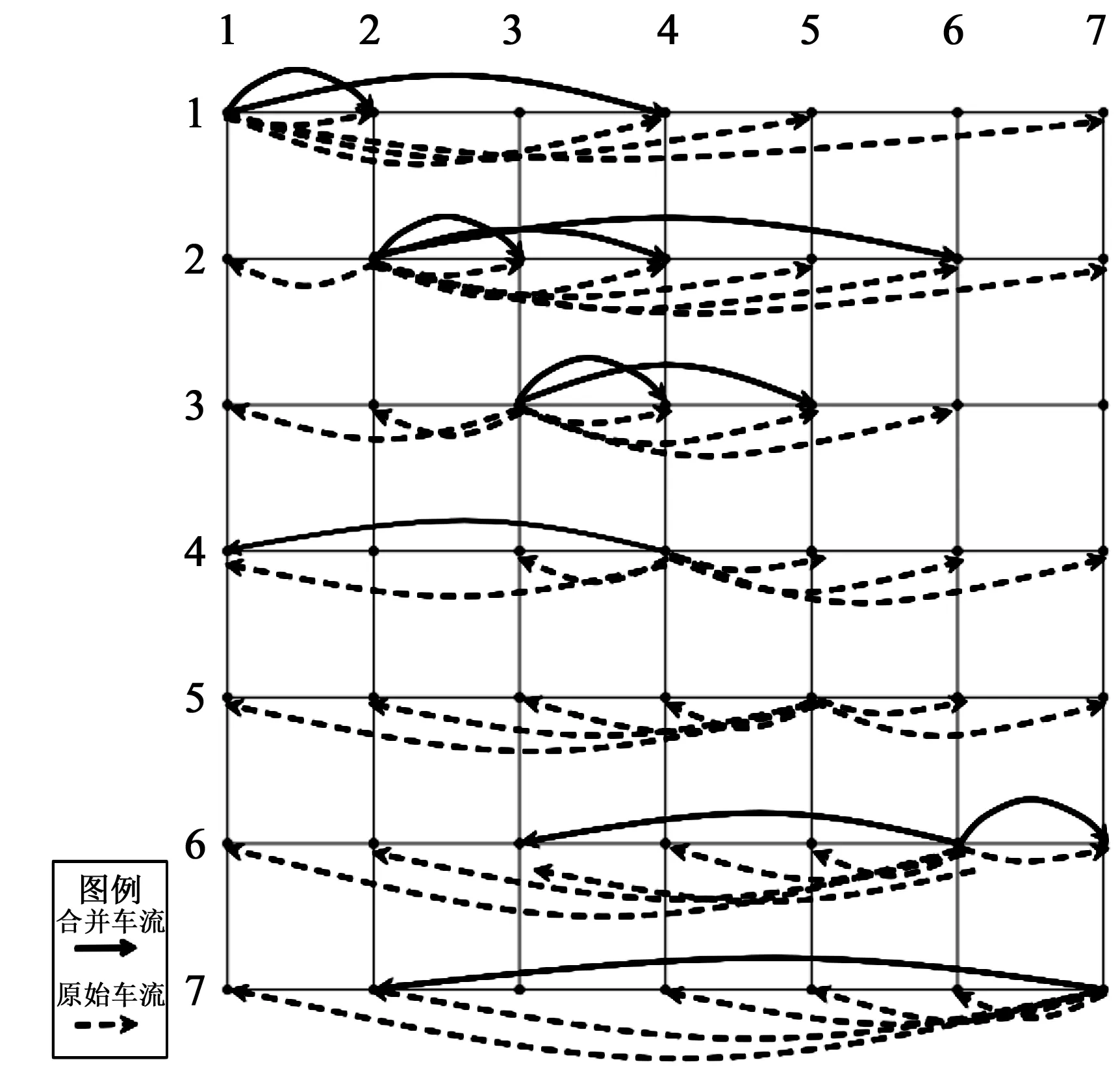
图6 车流合并情况示意图(运到期限1)Fig.6 Traffic flow merging situation (shipped to a period of 1)

以运到期限限制1为例作解释说明，原来的37条车流，经过车流组合，部分车流在途中进行了中转和摘挂作业。运到期限限制1条件下实际开行列车11条，如表3所示。车流合并情况如图6所示。运到期限限制2同理，在此不再赘述。规律显示，运到期限增大，模型的总成本减小。结果表明，当运到期限减小时，会导致某些开车的长车流因为不能满足开行条件而不能开车，因此在一定程度上增加了开行列数，也进一步导致开行成本的增加。

表3 货物快运服务网络鲁棒优化模型求解结果(运到期限1)

4 结语

铁路货物快运服务网络设计可以满足市场对铁路快运发展的要求，在实际铁路运输中，运输需求往往不能用一个定值去衡量，本文考虑到实际铁路货物快运需求的波动性，借鉴鲁棒优化思想，构建了铁路货物快运服务网络设计鲁棒优化模型，以提高求解结果的适用性，并采用和声搜索算法对模型进行求解。算例分析表明，本文采用的构模方式可以有效压缩网络规模，收敛速度快。本文给出的方法，能够为货物快运列车服务网络设计提供决策支持。但是，由于文中未考虑空车车底的回送可能会增加的运输成本，在下一步的研究中可以结合铁路货物快运服务网络设计和空车调配的问题进行综合考虑。

[1]张静. 我国铁路快捷货运班列开行方案研究[D]. 北京:北京交通大学, 2011.

[2]兰劲棕. 我国铁路快捷货物运输组织相关问题研究[D].成都:西南交通大学, 2011.

[3]许旺土. 综合快捷货运服务网络运输能力计算方法研究[D]. 北京:北京交通大学, 2010.

[4] MAIA L C, do COUTO A F. An innovative freight traffic assignment model for multimodal networks[J]. Computers in Industry, 2013, 64(2):121-127.

[5] BAI R B, WALLACE S W,LI J P, et al. Stochastic service network design with rerouting[J]. Transportation Research Part B Methodological, 2014, 60:50-65.

[6] HAJIAGHAEI-KESHTELI M, M AMINNAYERI. Solving the integrated scheduling of production and rail transportation problem by Keshtel algorithm[J]. Applied Soft Computing, 2014, 25:184-203.

[7]刘杰, 何世伟, 宋瑞,等. 铁路既有繁忙干线货运产品布局优化模型及算法[J]. 北京交通大学学报, 2013, 37(6):91-98.

[8]SOYSTER A L. Convex programming with set-inclusive constraints and applications to inexact linear programming[J]. Operations Research, 1973, 21(5):1154-1157.

[9] NAJAFI M,ESHGHI K,DULLAERT W. A multi-objective robust optimization model for logistics planning in the earthquake response phase[J]. Transportation Research Part E Logistics & Transportation Review, 2013, 49(1):217-249.

[10]李婷婷, 宋瑞. 国家层面综合客运枢纽分层布局鲁棒优化模型[J]. 东南大学学报(自然科学版), 2015, 45(1):189-195.

[11]LIU X C, HE S W, SONG R, et al. Robust optimization model and algorithm for railway freight center location problem in uncertain environment[J]. Computational Intelligence & Neuroscience, 2014, 2014:607159.

[12]郭玉华, 何世伟, 王保华. 铁路中转班列开行方案优化研究[J]. 铁道学报, 2011, 33(5):8-13.

[13]王保华, 何世伟. 不确定环境下物流中心选址鲁棒优化模型及其算法[J]. 交通运输系统工程与信息, 2009, 9(2):69-74.

[14]王莹, 刘军. 铁路行包快运专列开行方案优化编制方法的研究[J]. 交通运输系统工程与信息, 2007, 7(3):125-129.

[15]KHAN M B, ZHOU X S. Stochastic optimization model and solution algorithm for robust double-track train-timetabling problem[J]. IEEE Transactions on Intelligent Transportation Systems, 2010, 11(1):81-89.

[16]许越. 集装化运输模式下快捷货运服务网络优化设计研究[D]. 北京:北京交通大学, 2015.

DOI:10.3976/j.issn.1002-4026.2017.03.015

Robustness optimization model for freight express service network design scheme

LIU Xin-meng

(School of Economic Management, Xi′an Aeronautical University, Xi′an 710077, China)

∶As freight demand is prone to volatility during the planning period, robustness optimization model for freight express service network design was constructed in this paper. By comparing the robustness optimization model with the traditional basis model, and aiming at minimizing total transportation cost, the objective function has the implication of transportation services constraints, such as train transfers and train detaching as well as attaching plan, train marshaling plan, and delivery time, etc. The harmony search algorithm was used in this paper to solve the model with loop iteration to get better results. The results reveal that the robustness optimization model is well accustomed to the change in transportation demand, and it can also postpone freight delivery deadline while the transportation cost is reduced.

∶freight express; train service network design; robustness; harmony search

10.3976/j.issn.1002-4026.2017.03.012

2016-08-24

陕西省社会科学基金项目(2016D051)

刘欣萌(1990—)，女，助教，研究方向为交通运输现代组织管理理论与方法。E-mail：13120872@bjtu.edu.cn

U292.3

A

1002-4026(2017)03-0065-08