关于非平面图染色的一个猜想
2017-06-28张祥波
张祥波
(德州市临邑县临盘中学,山东 德州 251507)
关于非平面图染色的一个猜想
张祥波
(德州市临邑县临盘中学,山东 德州 251507)
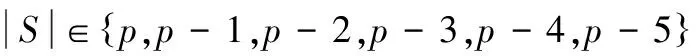
四色问题;顶点染色数;图的厚度;平面图

1 引言及预备知识
平面图的染色由于四色问题的计算机证明[3-5],而倍受国内外学者的广泛关注。而非平面图的染色由于缺少这样一个有价值和意义的问题,至今尚无进展。对于非平面图的染色,文献[6]猜想:χ(G)≤4θ(G)+θ2(G)-1。文献[7-9]证明了下述定理。
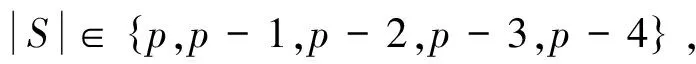
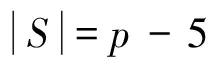
以下给出本文证明中用到的引理和定义。
定义1[2]如果图G含有的所有最大团存在公共顶点,且公共顶点的个数为k,则称此图为第k类图。
引理1[10]图G是二部图,当且仅当G中不含奇圈。
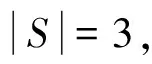
①若该公共顶点与图G-V′中的一个顶点不相邻,则χ(G)=3。
②若该公共顶点与图G-V′中的所有顶点相邻,且图G-V′存在奇圈,则χ(G)=4。
③若该公共顶点与图G-V′中的所有顶点相邻,且图G-V′不存在奇圈,则χ(G)=3。
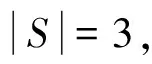
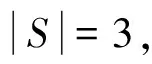

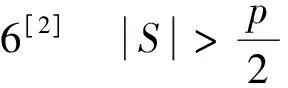
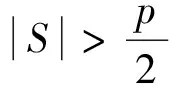
(1)V′(Gs)中任意一个顶点与V(G-V′)中的所有顶点相邻;
(2)图G是第p-4类图或第p-6类图;
则χ(G)=p-3。
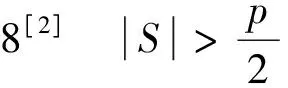
(1)V′(Gs)中任意一个顶点与V(G-V′)中的所有顶点相邻;
(2)图G是第p-5类图;
若图G-V′中不存在奇圈,则χ(G)=p-3;若图G-V′中存在奇圈,则χ(G)=p-2。
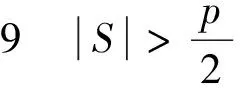


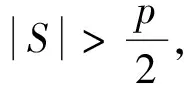
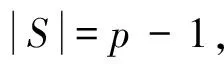
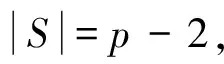
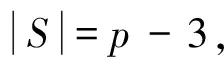
2 主要结果及证明
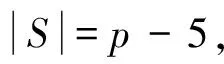
(1)p=7时,图G是顶点数等于7,含最大团K2的图。将图G中一对不相邻顶点u和v删掉后,必能得到一个顶点数是5,含最大团K2的图G1或仅有5个顶点的无边图。若图G1不存在奇圈,由引理1知,则图G1是二部图。于是χ(G1)=2,将u和v添上,色数最多增加1,故χ(G)≤3。若图G1存在奇圈,则图G1是一个5-圈,于是χ(G1)=3。而u至多和图G1中2个不相邻顶点相邻,于是u可以用图G1中的颜色染之。v的情况同u,v与u不相邻,故χ(G)≤3。
(2)p=8时,图G是顶点数等于8,含最大团K3的图。将图G中2个不相邻的顶点u和v删掉,必能得到顶点数是6,含最大团K3的图,记作G1。考虑图G1的色数,若图G1中所有最大团K3存在1个公共顶点,由引理2情况①或③知,则χ(G1)=3。于是χ(G)≤4。由引理2情况②知,χ(G1)=4。设图G1中所有最大团K3的公共顶点是w,若u与w相邻,则u至多与图G1-w中2个不相邻顶点相邻。而图G1-w是5-圈,故χ(G1-w)=3。所以u一定可以用图G1-w中的一种颜色染之。若u与w不相邻,则u与w可染同一种颜色。由于u与v不相邻,顶点v的情况与u相同,故顶点v的染色不影响图G的色数,所以χ(G)=4。若图G1中所有最大团存在2个公共顶点,由引理3知,χ(G1)=3,故χ(G)≤4。若图G1所有最大团K3不存在公共顶点,由引理4知,χ(G1)=3。故χ(G)≤4。
(3)p=9时,图G是顶点数等于9,含最大团K4的图。将图G中2个不相邻顶点u和v删掉,必能得到顶点数是7,含最大团K4的图,记作图G1。由定义1和引理9知,图G1有且仅有以下几类图:第1类图、第2类图、第3类图及只含有一个最大团K4的图。考虑图G1的色数,不外乎以下几种情况:若图G1分别满足引理5、引理6、引理7的条件,则由引理5、引理6、引理7分别知,χ(G1)=4;将顶点u和v添上,故χ(G)≤5。若图G1满足引理8的条件,则G1-V′是顶点数为5,含最大团K2的图。若图G1-V′不存在奇圈,故χ(G1)=4,将顶点u和v添上,于是χ(G)≤5。若图G1-V′存在奇圈,故χ(G1)=5。考虑顶点u,若u与V′中所有顶点相邻,则u至多与G1-V′中2个不相邻顶点相邻,从而u可以用图G1-V′中的颜色染之。若u与V′中至少一个顶点不相邻,则u总可以用V′中的颜色染之。v与u不相邻,v的情况同u,故χ(G)=5。
(4)p=10时,图G是顶点数等于10,含最大团K5的图。将图G中2个不相邻顶点u和v删掉,必得到顶点数是8,含最大团K4或K5的图G1。若图G1含最大团K4,由引理10知,χ(G1)≤5。添上顶点u和v,就得到原来的图G。而顶点染色数最多增加1,故χ(G)≤6。若图G1含最大团K5,分别由引理5、引理6、引理7知,χ(G1)=5。添上顶点u和v,故χ(G)≤6。若图G1满足引理8条件,G1-V′不存在奇圈,则χ(G1)=5。于是χ(G)≤6。G1-V′存在奇圈,则χ(G1)=6。u和v的情况同(3),于是χ(G)=6。
综上,定理为真。证毕。
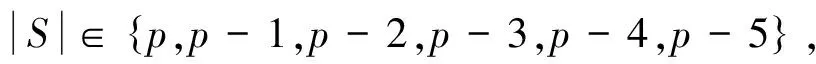
证明 考虑以下几种情况:
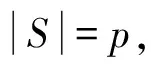
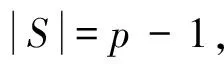
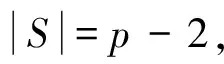
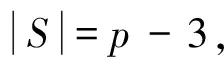

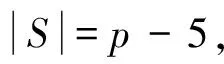
3 结语

[1]BONDY J, MURTY U. Graph theory[M]. Berlin: Springer, 2008.
[2] 张祥波. 一类特殊图的顶点染色数[J]. 安庆师范学院学报(自然科学版), 2015, 21(3): 11-13.
[3] APPEL K, HAKEN W. The solution of the four-color map problem[J]. Sci Amer,237(1977):108-121.
[4] APPEL K, HAKEN W, KOCH J. Every planar map is four-colorable. I: Discharging[J]. Illinois J Math, 1977 (21):429-490。
[5]APPEL K, HAKEN W. Every planar map is four-colorable. Ⅱ: Reducibility[J]. Illinois J Math, 1977 (21):491-561.
[6] 张祥波. 研究四色问题的意义及理论构想[J]. 数学理论与应用,2012,32(3):24-28.
[7] 张祥波, 魏志芹.关于图的色数与厚度的一些新结果[J]. 高师理科学刊,2013,33(5):35-37.
[8] 张祥波. 一类特殊图的顶点染色及其猜想的证明[J].重庆工商大学学报(自然科学版),2015,32(9):66-70.
[9] 张祥波.与图的顶点染色数有关的几个问题[J]. 高师理科学刊,2016,36(3):17-20.
[10] 谢政,戴丽. 组合图论[M]. 长沙:国防科技大学出版社,2003.
[11] 卜月华,吴建专,顾国华,等. 图论及其应用[M]. 南京:东南大学出版社, 2002.
A conjecture about coloring of non-planar graphs
ZHANG Xiang-bo
(Linpan Middle School,Dezhou 251507,China)

∶four-color problem; vertex coloring number; thickness of a graph; planar graphs
10.3976/j.issn.1002-4026.2017.03.016
2016-04-27
张祥波(1978—),男,研究方向为图的染色。E-mail:lpzx2010@126.com.
O157.5
A
1002-4026(2017)03-0094-04
