球形颗粒在含纤维幂律流体中沉降速度预测模型

刘庆岭，田守嶒，李根生，沈忠厚，许争鸣，庞照宇，王友文

中国石油大学(北京)油气资源与探测国家重点实验室，北京 102249

石油化学

球形颗粒在含纤维幂律流体中沉降速度预测模型

刘庆岭，田守嶒*，李根生，沈忠厚，许争鸣，庞照宇，王友文

中国石油大学(北京)油气资源与探测国家重点实验室，北京 102249

在石油工业中，纤维被广泛应用于提高钻井液和压裂液的固相运移能力，研究颗粒在含纤维流体中的沉降速度可以为纤维钻井液及压裂液性能评价与优化设计提供依据。本文针对球形颗粒在含纤维幂律流体中的沉降速度进行研究，拟建立一个考虑不同雷诺数与纤维浓度的颗粒沉降速度预测模型。开展了球形颗粒在含纤维幂律流体中沉降速度全参数实验，考虑的变量参数有：颗粒粒径、颗粒密度、基液流变性及纤维浓度。结果表明：在实验条件下，加入纤维使基液的表观黏度有少量增加；随着纤维浓度的增大，颗粒沉降速度逐渐降低，表明纤维对颗粒产生一个机械阻力作用，定义为纤维阻力。与黏性阻力系数类似，本文定义无因次纤维阻力系数来定量表征纤维阻力的大小；定义与颗粒沉降速度无关的阿基米德数为总阻力系数(纤维阻力系数与流体阻力系数之和)与颗粒雷诺数的函数。基于实验数据，发现在实验沉降速度下，颗粒雷诺数与无因次阿基米德数在双对数坐标系中符合线性关系，据此拟合得到了最终的颗粒沉降速度预测模型。与实验数据相比，该模型平均相对误差为12.39%，符合精度要求。该模型适用的雷诺数范围为(0.002～324)，纤维浓度范围为(0.02%～0.1%)。本研究对纤维在石油工程中的应用具有一定的指导意义。

球形颗粒；纤维；幂律流体；沉降实验；沉降速度；预测模型

0 引言

纤维在石油工业中应用广泛。在大斜度井及水平井钻井过程中，岩屑清洁十分困难，钻井液携岩能力差会降低机械钻速，增大扭矩，并造成卡堵和钻头磨损等问题[1]。纤维在钻井液中充分分散后，能够在不增加钻井液黏度的情况下显著增强其携岩能力，减少井下复杂工况和事故的发生[2-3]。在水力压裂过程中，一方面，压裂液携砂能力不足会导致裂缝闭合前支撑剂集中在裂缝底部，不能完全充填裂缝，影响产能[4]；另一方面，压裂施工后排液时，支撑剂回流现象普遍，不仅降低储层的改造效果，而且支撑剂在高速返排液的携带下会冲蚀井口阀门和地面管线，影响安全生产[5-6]。支撑剂回流产生的管线冲蚀问题对于压力高、流速快的气井更为突出[7]。纤维在压裂液中分散能够避免支撑剂的快速沉降，促进支撑剂完全均匀分布到整个裂缝中，提高产能[8]。压裂液返排过程中，纤维与支撑剂之间相互作用形成空间网状结构，增强支撑剂的内聚力，从而将将支撑剂稳定在原始位置，预防支撑剂的回流[9]。

研究颗粒在含纤维流体中的沉降速度可以为纤维钻井液及压裂液性能评价与优化设计提供依据。国内外学者对于颗粒在纯幂律流体中的沉降规律进行了大量研究，提出了多种模型，如Chhabra模型[10]，Kelessidis模型[11]，Shah模型[12]等。然而，针对颗粒在含纤维幂律流体的沉降问题国内外研究较少，并且主要为定性研究，缺乏定量评价。

笔者采用室内实验方法，测试球形颗粒在不同粒径、密度、纤维浓度与不同基液流变性条件下的沉降速度，进而对实验数据进行回归分析，最终得到了考虑不同颗粒雷诺数与纤维浓度的颗粒沉降速度预测模型。

1 实验装置及方法

1.1 实验装置

如图1所示，进行实验的沉降装置为有机玻璃圆筒，其内径为200 mm，高度为1 500 mm。使用高速摄影(Phantom v310)记录颗粒沉降过程，记录频率为100桢/秒。

图1 实验装置Fig. 1 Experimental setup

1.2 实验材料

实验所使用的球形颗粒材质为铝(Al)、钛(Ti)、钢(St) 3种，密度分别为2 680 kg/m3、4 450 kg/m3和 7 960 kg/m3，颗粒直径为1～10 mm。使用不同材质的颗粒一方面为了扩大颗粒的雷诺数范围(0.002～324)，另一方面为了能使所建立的模型对不同密度的颗粒均具有适用性。实验使用羧甲基纤维素(CMC)水溶液作为幂律流体基液，质量浓度范围为0.75%～1.75%，流变参数如表1所示。实验使用的纤维为美国FORTA公司生产，长度为3.175 mm，比重为1。

1.3 实验方案和步骤

实验为全参数实验，变量为：颗粒密度、颗粒直径、CMC浓度和纤维浓度。实验研究[3]及现场应用[8]表明，流体中加入少量的纤维(质量浓度≤0.1%)即可达到所需的固相运移效果。纤维含量超过临界值时会使得表观悬浮液黏度显著升高[13]。因此，本实验测试选用的纤维浓度范围为0.02%～0.1%。实验方案如表2所示，共需进行630(3×7×5×6)组实验。实验步骤如下：

(1)将所需的CMC粉末与清水在容器中混合，使用搅拌器以300 r/min的转速均匀搅拌至充分溶解，然后静置水化12 h。

(2)将一定质量的纤维加入CMC溶液中，边加边低速搅拌，直至纤维充分分散，形成稳定的悬浊液。

(3)使用流变仪(Hakke Rheostress 6000)测试流变参数。

(4)将配置好的实验溶液倒入沉降装置，静置15 min待气泡排出。

(5)颗粒在进行沉降实验前应首先在测试流体中浸泡12 h，以确保在实验过程中颗粒和流体能够充分接触。进行沉降实验时，颗粒应从圆筒容器中心液面之下投入。整个实验过程中温度应保持恒定。

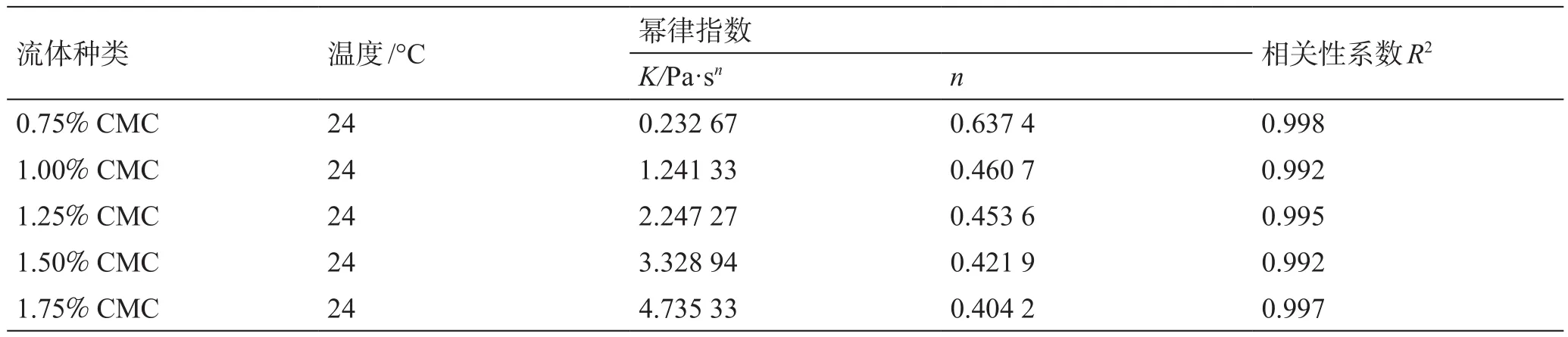
表1 不同浓 度CMC溶液的流变性Table 1 Rheological properties of fl uids with different CMC concentrations

1.4 数据处理方法

高速摄影的记录范围设置为距圆筒上端700 mm以下到下端300 mm以上，在这个范围内既能确保颗粒已经达到沉降速度，又能避免壁面的边界效应对沉降速度的影响。如图2所示，在高速摄影记录范围内，T时刻到T+ΔT时刻范围内球形颗粒下降了ΔL距离，则颗粒的沉降速度为V=ΔL/ΔT。每组实验至少重复三次，直至有三组数据平均相对误差小于5%。

表2 实验方案Table 2 Experimental scenarios

2 实验结果和讨论

2.1 纤维对流体流变性的影响

图3所示为0.75% CMC溶液不同纤维浓度下流变性测试及幂律拟合曲线，相关性系数R2均大于0.99，表明含纤维悬浮液流变方程符合幂律模式。选用剪切速率γ=511 s-1，由公式(1)计算不同纤维浓度下表观黏度。拟合得到的幂律指数和计算得到的表观黏度如表3所示。对比不同纤维浓度下的表观黏度，发现纤维质量浓度小于等于0.06%时，表观黏度相对于基液有上下波动，但变化较小，相对改变量Δμn小于3%；纤维质量浓度为0.08%和0.10%时，表观黏度相对于基液有少量增加，相对改变量Δμn分别等于9.09%和9.92%。

其中：τ为剪切应力，Pa；γ为剪切速率，s-1。

2.2 纤维对颗粒沉降速度的影响

如图4所示，取出部分含纤维流体，选用高速摄影高放大倍数镜头拍摄，发现纤维细丝分散在流体中，相互交叉缠绕，呈现稳定的网状结构。如图5所示，对于不同直径的颗粒，随着纤维浓度的增加，颗粒沉降速度均平缓下降,表明分散在流体中的纤维网络对颗粒施加了附加的阻力作用，定义为纤维阻力，且随着纤维浓度的升高，阻力逐渐增大。实验中还发现，CMC浓度大于等于1.25% 时，随着纤维浓度的增加，粒径较小的铝颗粒(dp=1 mm，2 mm)逐渐趋向于完全悬浮，其原因在于纤维网状结构相当于使流体产生了静切力[14]，粒径较小的铝颗粒浮重较小无法克服静切力，因而悬浮在含纤维流体中，沉降速度为零。

图2 球形颗粒沉降过程中捕捉图片Fig. 2 The settle-capture photographs of sphere

图3 0.75% CMC溶液不同纤维浓度下流变性测试Fig. 3 Rheologies of 0.75% CMC fl uids with different fi ber concentrations

表3 0.75%CMC溶液不同不同纤维浓度下幂律指数和表观黏度Table 3 Fitted power-law parameters and apparent viscosity of 0.75% CMC fl uids with different fi ber concentrations

图4 纤维网状结构微观图像Fig. 4 The microscope image of fi ber network structure.

3 沉降速度计算模型

3.1 颗粒受力分析

如图6所示，球形颗粒在含纤维流体中自由沉降时，受到三个力的作用：一是颗粒在流体中的浮重，Fw0(重力与浮力之差)；第二是流体作用于颗粒表面的阻力，称为流体阻力Fdv；第三类是纤维作用于颗粒表面的阻力，定义为纤维阻力Fdf。

颗粒在流体中的浮重，Fw0，只取决于颗粒的重度和流体的重度，与颗粒速度无关，其表达式为：

其中：dp为颗粒直径，m；ρp为流体密度，kg/m3；ρf为流体密度，kg/m3；g为重力加速度，m/s2。

颗粒受到的总阻力为纤维阻力和流体阻力之和：

体阻力表达式为：

其中：v为颗粒瞬时速度，m/s；Cdv为流体阻力系数。

Rida Elgaddaf i等[15-16]通过实验研究表明，纤维阻力与流体阻力存在共性，纤维阻力Fdf可以表达为与流体阻力Fdv类似的形式。与流体阻力系数Cdv形式类似，本文定义纤维阻力系数Cdf表达式为：

定义总阻力系数Cdt为纤维阻力系数与流体阻力系数之和：

将公式(4)、(5)、(6) 带入公式(3)，得到颗粒所受的总阻力Fdt表达式为：

颗粒受到的总阻力Fdt与颗粒浮重FW0相等时，颗粒加速度为0，达到沉降速度，即v=V，联立公式(2)和(7)，从而得到颗粒达到沉降速度V时的总阻力系数表达式：

3.2 模型建立

对于幂律流体，颗粒雷诺数Rep表达式为：

Chahabra等[10]通过将颗粒在纯幂律流体中达到沉降速度时的雷诺数Rep与流体阻力系数Cdv结合，提出一个与颗粒沉降速度无关的无因次数，称之为阿基米德数，用Ar表示：

通过对400多组实验数据进行拟合，最终回归得到颗粒在纯幂律流体中的沉降速度预测方程，如式(11)所示，与实验数据平均相对误差为14.1%，

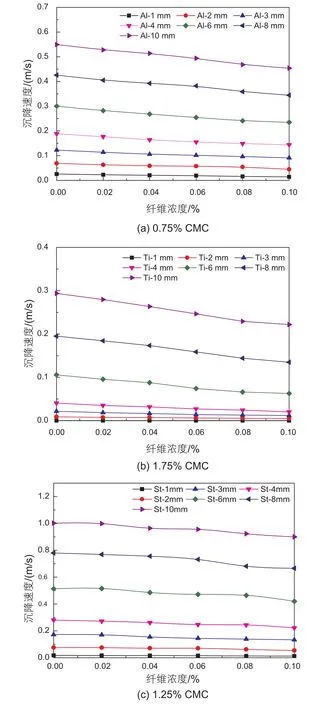
图5 不同纤维浓度下颗粒沉降速度Fig. 5 Settling velocity vs. fi ber concentration in test fl uids.

本文借鉴该模型处理方法，将颗粒在含纤维幂律流体中达到沉降速度V时颗粒雷诺数Rep与总阻力系数Cdt结合得到：

将式(8)、(9)带入式(12)，最终得到与颗粒沉降速度无关的阿基米德数Ar表达式：

基于实验测得的颗粒沉降末速V，根据公式(9)计算颗粒雷诺数Rep，并计算对应的阿基米德数Ar。如图7所示，在双对数坐标系中，阿基米德数Ar与颗粒雷诺数Rep符合线性关系，拟合曲线可由方程(14)表示，平均相关系数R2为0.99。不同的CMC浓度和纤维浓度Cf组合条件下，参数A和B的拟合结果分别为表4(a)、4(b)所示，平均相对误差为10.4%，

从表4(a)、4(b)可以看出，参数A、B随纤维浓度Cf和CMC浓度变化而变化，不同的CMC浓度可由无因次流性指数n表征。因而，A、B为流性指数n和纤维浓度Cf共同确定的二元函数，即：

其中：f、g均为函数符号。

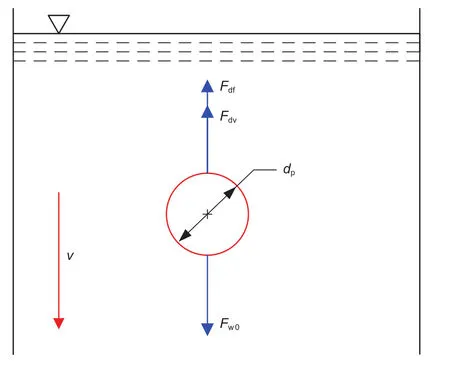
图6 球形颗粒在含纤维幂律流体中自由沉降示意图Fig. 6 Schemadic diagram of sphere settling in fi ber containing power-law fl uid

图7 不同纤维浓度和CMC浓度条件下颗粒雷诺数Rep随阿基米德数Ar变化Fig. 7 Ar number vs. Repwhen particles reach settling velocity

首先确定参数A、B和纤维浓度之间的函数关系。图8所示为参数A和B随纤维浓度Cf变化及最小二乘拟合曲线。 A随纤维浓度Cf的增加线性下降，平均相关性系数R2为0.97。B随纤维浓度Cf的增加线性增大，平均相关性系数R2为0.95。拟合曲线可分别由公式(17)、(18)表示，A1，A2，B1和B2均为关于流性指数n的一元函数。

表4 不同测试流体下参数A和B拟合结果Table 4 Fitting results of parameter A and B for different test fl uids (a)参数A拟合结果

表5 参数A1和A2线性拟合值Table 5 Fitting results of parameters A1and A2

表6 参数B1和B2线性拟合值Table 6 Fitting results of parameters B1and B2

图9 参数A1和A2随n变化Fig. 9 Parameter A1and A2vs. n

不同CMC浓度条件下，线性拟合参数A1，A2的值如表5所示，平均相对误差为3.73%，最大相对误差为5.95%。

不同CMC浓度条件下，线性拟合参数B1，B2的值如表6所示，平均相对误差为2.61%，最大相对误差为5.94%。

然后，基于表5和表6，分别拟合参数A1、A2、B1、B2与流性指数n的函数关系。图9所示为A1和A2随n变化及最小二乘拟合曲线，相关性系数R2分别为0.96和0.99，得到公式(19)、(20)，

图10所示为B1和B2随n变化及最小二乘拟合曲线，相关性系数R2分别均为0.93，得到公式(21)、(22)，综合公式(14)、(17)、(18)、(19)、(20)、(21)、(22)，最终得到沉降速度预测公式：

图10 参数B1和B2随n变化Fig. 10 Parameter B1and B2vs. n

图11所示为根据预测模型计算得到的沉降速度与实验测得的沉降速度对比，平均相对误差为12.39%，最大相对误差为36.73%。分析认为误差来源有两方面：一方面为测量产生的误差。颗粒沉降速度较小时，沉降时间较长，易受环境影响，不易获得准确的沉降速度；另一方面为数据拟合过程产生的误差。基于实验数据拟合得到的经验模型，同样存在一定的偏差。

3.3 算例

算例所采用的颗粒和流体性质如表7所示。将基础参数代入公式(23)，计算得到：A=-2.533 9，B=2.057 4，Ar=3.053 9，从而V=0.012 2 m/s。实验测得该颗粒沉降速度为0.011 6 m/s，与实验数据相比，模型预测相对误差为5.17%。

图11 预测沉降速度与实验沉降速度对比Fig. 11 Comparison of measured and predicted settling velocity calculated using explicit equation.

表7 颗粒和流体性质Table 7 Fluid and sphere properties

4 结论

本文采用室内实验的方法，研究了球形颗粒在不同粒径、密度、纤维浓度与CMC浓度条件下的沉降规律，进而通过对实验数据进行回归分析，最终得到了颗粒沉降速度预测模型，获得了以下几点认识：

(1)纤维质量浓度≤0.06% 时，表观黏度相对于基液有上下波动，但变化较小，相对改变量小于3%；纤维质量浓度为0.08%和0.10%时，表观黏度相对于基液有少量增加，相对改变量别等于9.09%和9.92%。

(2)球形颗粒沉降速度随纤维浓度增大逐渐降低，表明纤维网络对颗粒施加了附加的阻力作用，且随纤维浓度的增加，附加阻力增大。

(3)定义了无因次纤维阻力系数来定量表征纤维阻力的大小；定义了与颗粒沉降速度无关的阿基米德数为总阻力系数(纤维阻力系数与流体阻力系数之和)与颗粒雷诺数的函数。基于实验数据，发现颗粒雷诺数与无因次阿基米德数符合幂律关系。

(4)通过回归分析建立颗粒沉降时的雷诺数与无因次阿基米德数的关联方程，最终得到了颗粒沉降速度预测模型。

(5)与实验数据相比，该模型平均相对误差为12.39%，最大相对误差为36.73%。该模型适用的雷诺数范围为(0.002～324)，纤维浓度范围为(0.02%～ 0.1%)。

符号说明

符号

希腊字母

[1] CAYEUX E, MESAGAN T, TANRIPADA S, et al. Real-time evaluation of hole-cleaning conditions with a transient cuttings-transport model[J]. Spe Drilling & Completion, 2014, 29(1)： 5-21.

[2] 艾贵成, 王卫国, 穆辉亮, 等. 超级纤维清扫液工艺的应用[J]. 钻井液与完井液, 2008, 25(6)： 85-6. [AI G C, WANG W G, MU H L, et al. The application of super fi ber sweeps techniques[J]. Drilling Fluid & Completion Fluid, 2008, 25(6)： 85-86.]

[3] AHMED R, TAKACH N. Fiber sweeps for hole cleaning[J]. Spe Drilling & Completion, 2009, 24(4)： 564-573.

[4] 刘彝, 吴均, 刘京, 等. 纤维基压裂液[J]. 钻井液与完井液, 2009, 26(6)： 88-90. [LIU Y, WU J, LIU J, et al. A cellulosic fracturing fl uid[J]. Drilling Fluid & Completion Fluid, 2009, 26(6)： 88-90.]

[5] 赵建平, 何世云, 宋永华, 等. 高压高产气井预防砂刺的综合措施研究[J]. 石油钻采工艺, 2007, 29(4)： 51-54. [ZHAO J P, HE S Y, SONG Y H, et al. Comprehensive measures to prevent sand thorn in high pressure and high production gas well[J]. Oil Drilling & Production Technology, 2007, 29(4)： 51-54.]

[6] 任斌, 刘国良, 张冕, 等. 苏里格气田加纤维压裂技术的应用研究[J]. 西南石油大学学报(自然科学版), 2014, 36(1)： 121-128. [REN B, LIU G L, ZHANG M, et al. Application research of fi ber fracturing technology at sulige gas fi eld[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2014, 36(1)： 121-128.]

[7] 任山, 向丽, 黄禹忠, 等. 纤维网络加砂压裂技术研究及其在川西低渗透致密气藏的应用[J]. 油气地质与采收率, 2010, 17(5)：86-89. [REN S, XIANG L, HUANG Y Z, et al. Study on fi ber network sand fracturing technique and application in the low permeablereservoir of chuanxi area[J]. Petroleum Geology and Recovery Eff i ciency, 2010, 17(5)： 86-89.]

[8] ENGELS J N, MARTINEZ E, FREDD C N, et al. A mechanical methodology of improved proppant transport in low-viscosity fl uids：application of a fi ber-assisted transport technique in east texas[C]. SPE Eastern Regional Meeting. Charleston, West Virginia：Society of Petroleum Engineers, 2004.

[9] 周林刚. 纤维加砂压裂工艺研究及应用[J]. 西部探矿工程, 2010, 22(11)： 92-95. [ZHOU L G. Study and application of fi ber sand fracturing technology[J] West-China Exploration Engineering, 2010, 22(11)： 92-95.]

[10] CHHABRA R P, PERI S S. Simple method for the estimation of free-fall velocity of spherical particles in power law liquids[J]. Powder Technology, 1991, 67(3)： 287-290.

[11] KELESSIDIS V C. An explicit equation for the terminal velocity of solid spheres falling in pseudoplastic liquids[J]. Chemical Engineering Science, 2004, 59(21)： 4 437-4 447.

[12] SHAH S N, FADILI Y E, CHHABRA R P. New model for single spherical particle settling velocity in power law (visco-inelastic) fl uids[J]. International Journal of Multiphase Flow, 2007, 33(1)： 51-66.

[13] GEORGE M, ELGADDAFI R, AHMED R, et al. Performance of fi ber-containing synthetic-based sweep fl uids[J]. Journal of Petroleum Science and Engineering, 2014, 119： 185-195.

[14] SWERIN A. Rheological properties of cellulosic fi bre suspensions fl occulated by cationic polyacrylamides[J]. Colloids and Surfaces A：Physicochemical and Engineering Aspects, 1998, 133(3)： 279-294.

[15] ELGADDAFI R, AHMED R, GEORGE M, et al. Settling behavior of spherical particles in fi ber-containing drilling fl uids[J]. Journal of Petroleum Science and Engineering, 2012, 84： 20-28.

[16] ELGADDAFI R, AHMED R, GROWCOCK F. Settling behavior of particles in fiber-containing Herschel Bulkley fluid[J]. Powder Technology, 2016, 301： 782-793.

Prediction model for settling velocity of solid spheres in fi ber containing power-law fl uids

LIU Qingling, TIAN Shouceng, LI Gensheng, SHEN Zhonghou, XU Zhengming, PANG Zhaoyu, WANG youwen
State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum-Beijing, Beijing 102249, China

In petroleum industry, fi ber containing fl uids are widely used to improve solid transport capacity of drilling/fracturing fl uids. The settling velocity of particle in fi ber containing fl uids is studied to provide basis for the evaluation and optimization of the fi ber drilling/fracturing fl uid performance. The purpose of current study is to develop the prediction model, suitable for different particle Reynolds numbers and fi ber concentrations, for settling velocity of solid spheres in fi ber containing power-law fl uids. Settling tests were conducted in fi ber containing power-law fl uids, and 4 crucial factors were considered, involving fl uid rheology, sphere diameter, particle density and fi ber concentration. Results show that adding a small amount of fi ber makes a minor increase in the apparent viscosity of the base fl uids under the experimental condition, and sphere settling velocity drops slowly with fi ber concentration increasing. It indicates that an additional drag force, def i ned as fi ber frag force, is applied to the sphere by fi ber network. Similar to the def i nition of the viscous drag coeff i cient, the fi ber drag coeff i cient is def i ned to quantify the fi ber drag force. the dimensionless number known as Archimedes number is def i ned by combining total drag coeff i cient (sum of the fi ber drag coeff i cient and viscous drag coeff i cient) and Reynolds number. The Archimedes number and Reynolds number follows linear relationship in the log-log plot. Finally, the prediction model for settling velocity of solid spheres is obtained by the regression equation of the Archimedes number and particle Reynolds number. The model predicts settling velocity in good agreement with measured settling velocity, with average relative difference of 12.39%. The model is valid for a range of particle Reynolds number (0.002-324) and fi ber concentration (0.02%-0.1%). This study is with the guiding signif i cance for the better application of fi ber in petroleum engineering.

sphere; fi ber; power-law fl uid; settling experiment; settling velocity; prediction model

10.3969/j.issn.2096-1693.2017.02.028

(编辑 马桂霞)

刘庆岭, 田守嶒, 李根生, 沈忠厚, 许争鸣, 庞照宇, 王友文. 球形颗粒在含纤维幂律流体中沉降速度预测模型. 石油科学通报, 2017, 02： 298-308

LIU Qingling, TIAN Shouceng, LI Gensheng, SHEN Zhonghou, XU Zhengming, PANG Zhaoyu, WANG Youwen. Prediction model for settling velocity of solid spheres in fi ber containing power-law fl uids. Petroleum Science Bulletin, 2017, 02： 298-308.doi：10.3969/ j.issn.2096-1693.2017.02.028

*通信作者, tscsydx@163.com

2017-01-17

国家自然科学基金石油化工联合基金重点基金项目(U1562212)和国家自然科学基金面上项目(516742745)联合资助