煤层气水平井压力饱和度关系及半解析生产预测模型
2017-06-28钟子尧吴晓东韩国庆
钟子尧,吴晓东,韩国庆
中国石油大学(北京),北京 102249
煤层气水平井压力饱和度关系及半解析生产预测模型
钟子尧,吴晓东*,韩国庆
中国石油大学(北京),北京 102249
煤层气藏数值模拟是煤层气水平井历史数据拟合以及生产预测的有效工具,但是计算耗时长,所需参数多。为了得到一个简单而精度足够的生产预测方法,由稳态解析的产能方程结合非稳态的边界条件可以得到煤层气井在线性流下的半解析模型。根据煤层气水平井的数值计算结果以及前人的研究成果,煤层在一维(线性或径向)非稳态渗流阶段流体饱和度和压力的关系随时间、空间变化不明显。本文通过煤层渗流控制方程推导了压力和饱和度的计算模型,并给出了由地层压力近似计算含水饱和度的方法,为气水两相渗流模型提供了计算基础。通过半解析模型与数值计算结果的对比,以及对沁水盆地两口水平井的历史数据拟合,验证了半解析模型的正确性和实用性。
煤层气;两相拟压力;生产预测;吸附解吸;两相渗流
0 引言
煤层气开采技术日趋成熟,产气量不断提高,成为一种重要的非常规油气资源,但同时也面临着低渗透的挑战。水平井及其配套压裂技术成为低渗煤层气藏开发的必要手段。低渗条件下渗流过程存在很长一段非稳态流动阶段[1],并且当地层压力高于煤层基质解吸压力时,地层流动为单相水渗流,随着排水作业的进行,地层压力下降到解吸压力以下,煤层气从基质中解吸出来,进入裂缝,这时流动变为气水两相渗流。为了预测一套排水降压制度的开发效果,油气藏数值模拟器常被用来模拟煤层气井产量变化以及地层气水动态分布。但是数值模拟方法建模工作量大,模型计算耗时长,不利于对多个排水制度进行优选。所以需要一种更为简单而且精度足够的方法,用来预测煤层气井生产动态或者根据气井目前的生产数据进行生产动态分析。
Clarkson(2015)在凝析气藏和黑油油藏半解析渗流模型的基础上[1],忽略气液两相间物质交换,并考虑煤层岩石对气体的吸附特性,建立了煤层气水平井的生产预测模型[2]。Clarkson研究表明煤层在不稳定渗流阶段,压力和饱和度之间存在一定关联,并通过数值模拟方法给出了压力和饱和度的关系曲线,用以计算气水产量。但是使用数值模拟方法给半解析模型提供计算参数,使得半解析方法失去其优势和意义。本文将从煤层气藏的一维渗流控制方程出发,推导压力和饱和度关系的解析方程,并与煤层气水平井数值模拟结果进行对比,最后应用半解析模型对实际气井进行生产数据拟合和预测。
1 气水两相半解析模型的建立
1.1 拟稳态模型
调查距离(Distance of investigation, DOI)在油气井测试中表征压力波瞬时传播的距离,常用来研究井与边界的距离以及与边界、邻井之间的相互影响[1]。根据调查距离的概念可知,调查距离以内地层为向油气井提供流体的区域,而调查半径以外的油气水不会受到此井的影响。随着生产的进行,调查距离从近井地带向地层深处移动,本文使用动态调查距离来表征地层中非稳态渗流过程,其随时间移动的位置可由(1)式计算得到[1]。对于水平井生产而言,地层中线性流占主导地位,因此可以假设由调查距离确定的地层区域内流体以垂直水平井方向流入井筒,如图1所示,调查区域的大小,平均压力以及平均饱和度随时间的变化是影响水平井生产的地层因素。

式中:xinv为调查区域的外边界随时间移动的距离,m,如图1所示;ki为煤层裂缝初始渗透率,md;φ为初始裂缝孔隙度,小数;μwi为水相黏度,mPa·s;cti为初始压力下的综合压缩系数,MPa-1;t为生产时间,d;Wattenbarger(1998)给出了在定流量生产和定井底流压生产下系数δ分别为0.416和0.588[3]。δ作为可拟合参数,在变井底流压以及气水、油气两相渗流情况下,Clarkson(2015)继续使用了0.588的值,并给出了根据数值方法计算系数δ的方法[4]。
Musket(1937)提出将地层中一段时间内的复杂瞬时流动,视为简单的拟稳态流动,整个渗流过程由一个个拟稳态过程连接而成[5]。Lee(1998)使用拟稳态的处理方法给出了气藏衰竭开采条件下,水平井生产的动态预测模型,他的模型中地层为单气相流动[6]。Clarkson(2015)通过引入油气两相拟压力,建立了煤层气水平井的半解析模型[2],如式(2)~(5)所示。水平井半解析模型假设地层为一维流动,地层中存在单相以及两相流动,由于地层渗透率低,泄油区域向外波及的速度慢,并未到达边界。根据这四个非线性方程使用Newton-Raphson迭代方法便可求解每一时间步上的平均压力和含水饱和度,以及水平井产气量qg和产水量qw[2]。


图1 调查区域内非稳态线性渗流Fig. 1 Unsteady linear fl ow in the investigation area

式中:krw和krg分别为水相相对渗透率和气相相对渗透率;μw和μg分别为水相和气相黏度,mPa·s;k为不同压力下的渗透率,md;Z为气体压缩因子。
1.2 压力与饱和度关系
在拟压力表达式(6)(7)的积分项中,除了与压力相关的变量(流体物性和渗透率)外,还有由饱和度决定的相对渗透率。根据Clarkson(2015)[2]等人的研究,低渗煤层在非稳定流状态下,压力、饱和度的关系随时间变化不大。从煤层气井的数值模拟结果(如图2和图3所示)中也能得到这样的结论。为了简化模型,可以认为压力和饱和度的关系是固定的。
Bφe等人(1989)[10]和Behmanesh(2015)[11]分别给出了径向流和线性流下压力和饱和度之间的关系表达式。参照他们的推导过程,线性流条件下,煤层气渗流控制方程如下(为了避免单位换算,下面公式均使用国际标准单位):
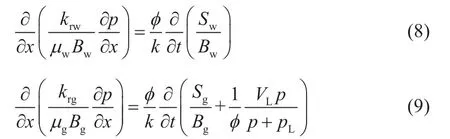


由于ds/dp=K/N,当0a>时由(10)、(11)两式可以消去dN/dy项得到(12)式,当=0a即气体渗透率为0时,若地层压力高于解吸压力,认为水相饱和度为1,若压力小于等于解吸压力,由式(9)左端等于0以及,可以得到(13)式。

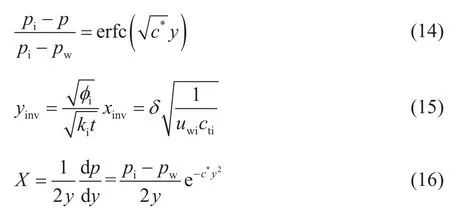
为了验证(12)(13)式的正确性,将计算得到的压力和饱和度关系与数模结果进行对比,如图2和图3所示。图中实线为式(12)(13)计算结果,散点为使用数值模型计算地层中不同位置在不同时间下的压力和饱和度结果。计算模型为小节2中所建立的数值实例井,并通过改变地层含气量(如图2所示)和气井井底流压(如图3所示)验证了在不同条件下,煤层中含水饱和度与压力存在对应关系。地层兰氏体积越大,则一定地层压力下解吸气体越多,对应的含气饱和度也越高。从图3看出,井底流压降低,也能提高含气饱和度,但不同井底流压下的曲线在高压段重合,只在低压段饱和度出现变化。在实际应用时式(16)中pw取最终稳定生产阶段的井底流压。
2 模型求解与应用

图2 不同含气量下压力和含水饱和度的关系Fig. 2 The relationship between pressure and water saturation under different gas content

图3 不同井底流压下压力和含水饱和度的关系Fig. 3 The relationship between pressure and water saturation under different bottom hole fl owing pressure
为了验证模型精度,使用文献[4]中的虚拟井参数将模型计算结果与数值方法计算结果进行了对比,并选择了沁水盆地柿庄南地区的两口水平井,根据本文建立的水平井半解析模型进行了历史拟合。式(1)中的参数δ、地层渗透率k可以用来快速拟合生产数据,缩小气水产量与实际产量的差距,而气水的相对渗透率曲线可以用来进一步调整气水产量的相对大小。表1和表2给出了煤层条件,水平井参数和流体物性。根据图4~图6中的井底流压,使用半解析模型式(2)~(5)计算煤层水平井排水初期的生产动态。图4中虚线为使用油气藏数值模拟软件ECLIPSE的煤层气模块计算得到的水平井生产动态,计算模型为盒状地层中心一口水平井,地层中气体吸附解吸特性满足Langmuir方程,并且吸附解吸为瞬时过程。从图中看出,半解析模型结果与数值结果的误差在10%以内,因此半解析模型可以认为是理论解的有效近似。
图5与图6为现场实例井生产数据以及根据式(2)~(5)计算的产气产水量,其中W1井为高含气井,产气压力为3.9 MPa,见气前排水作业以0.02 MPa/d的速度降压生产,见气后加快排水速度到0.033 MPa/d。W1井开井326天后产气量为7 466 m3/d,根据(6)(7)式拟合得到煤层物性参数,随后气井的生产按定井底流压进行预测,在生产380天左右达到最大产气量7 780 m3/d。W2井为低含气井,地层含气量低,生产资料显示解吸压力只有2.19 MPa,产气量低于1 000 m3/d,生产320天以后,将井底流压从1 MPa降到0.5 MPa,产气量增大到2 000 m3/d。如图5、6所示,半解析模型计算的产气速度与气井不同井底流压阶段的实际产量总体相符,计算结果与实际生产数据之间的平均误差可由式(17)进行计算,两口井日产气量平均误差分别为6.1%和9.9%,最终累计产气量误差分别为2.7%和2.3%,说明半解析模型可以满足应用要求。

表1 气水两相半解析模型历史拟合储层参数Table 1 Input parameters of reservoir for the semi-analytical model
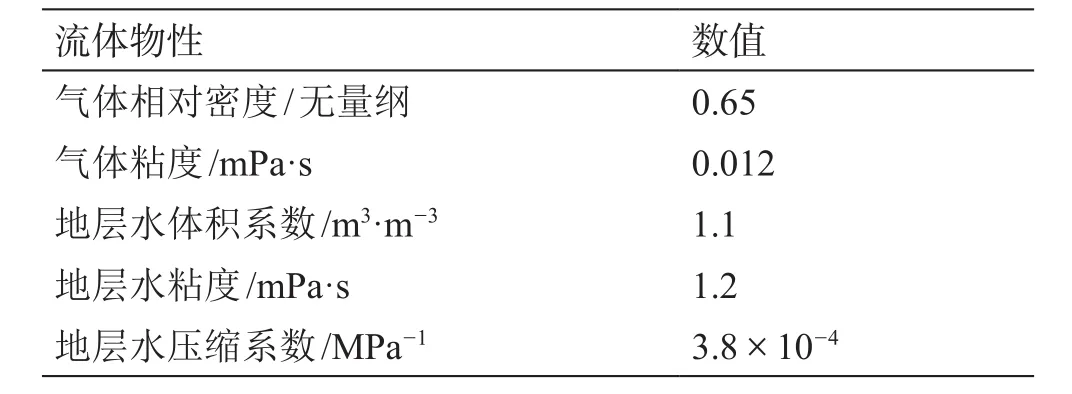
表2 模型计算流体物性参数Table 2 Fluid property parameters for the semi-analytical model

图4 数值计算结果与模型计算结果对比Fig. 4 The result contrast of numerical and semi-analytical method

图5 W1井生产数据分析与模型拟合结果Fig. 5 W1 well production data analysis and history match
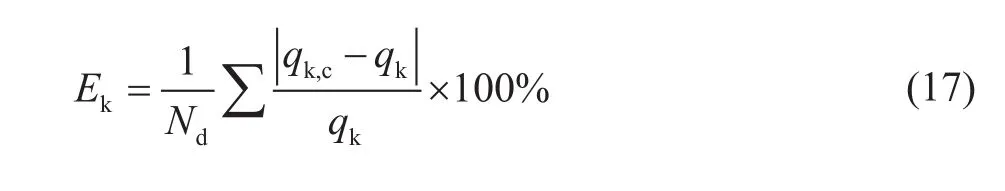
式中:E为计算误差,%;下标k={l,g}分别表示气水两相;qk为实际生产的气水产量,下标c表示半解析模型计算得到的气水产量,m3/d;Nd为气井生产天数,d。

图6 W2井生产数据分析与模型拟合结果Fig. 6 W2 well production data analysis and history match
3 结论
(1) 根据煤层气水平井数值模拟结果可知,在煤层气水平井生产过程中地层各点的压力和饱和度存在对应关系,并且随时间变化不大。
(2) 通过煤层气渗流控制方程推导出压力和饱和度关系的计算模型及其近似求解方法,计算结果与数值结果误差较小。
(3) 使用煤层气水平井半解析模拟对实际井生产动态进行拟合和预测,计算结果与实际生产数据的误差在可接受范围内,煤层气水平井半解析模型具有合理性和实用性。
[1] CLARKSON C R, QANBARI F. History matching and forecasting tight gas condensate and oil wells by use of an approximate semianalytical model derived from the dynamic-drainage-area concept[R]. Spe/csur Unconventional Resources Conference, 2015.
[2] CLARKSON C R., QANBARI F. A semi-analytical method for forecasting wells completed in low permeability, undersaturated cbm reservoirs[J]. Journal of Natural Gas Science & Engineering. 2016, 30: 19-27.
[3] WATTENBARGER R A, EL-BANBI A H, VILLEGAS M E, et al. Production analysis of linear fl ow into fractured tight gas wells[R].SPE Rocky Mountain Regional/Low-Permeability Reservoirs Symposium, 1998. .
[4] CLARKSON C R, QANBARI F. Transient fl ow analysis and partial water relative permeability curve derivation for low permeability undersaturated coalbed methane wells[J]. International Journal of Coal Geology, 2015, 152: 110-124.
[5] SHAHAMAT M S, MATTAR L, AGUILERA R. A physics-based method to forecast production from tight and shale petroleum reservoirs by use of succession of pseudosteady states[J]. Spe Reservoir Evaluation & Engineering, 2015, 18(4): 508-521.
[6] LEE K S, MILLER M A, SEPEHRNOORI K, et al. Succession-of-states model for calculating long-time performance of depletion reservoirs[J]. SPE Journal, 1996, 3(3): 279-284.
[7] 郝斐, 张公社, 刘东, 等. 用广义拟压力法确定产液气井流入动态[J]. 石油钻采工艺, 2003, 25(6): 54-56. [HAO F, ZHANG G S, LIU D, et al. Computing gas well inf l ow performace relationship by generalized pseudo-pressure[J]. OIL DRILLING & PRODUCTION TECHNOLOGY. 2003, 25(6): 54-56.]
[8] 冯其红, 舒成龙, 张先敏等. 煤层气井两相流阶段排采制度实时优化[J]. 煤炭学报. 2015, 40(1): 142-148. [FENG Q H, SHU C L, ZHANG X M, et al. Real-time optimization of drainage schedule for coalbed methane wells at gas-water two-phase fl ow stage[J]. Journal of China Coal Society, 2015, 40(1): 142-148.]
[9] 陈振宏, 陈艳鹏, 杨焦生, 等. 高煤阶煤层气储层动态渗透率特征及其对煤层气产量的影响[J]. 石油学报, 2010, 31(6): 966-969. [CHEN Z H, CHEN Y P, YANG J S, et al. Reservoir dynamic permeability of high rank coal bed methane and its effect on the coalbed methane output[J]. ACTA PETROLEI SINICA. 2010, 31(6): 966-969.]
[10] BØE A, SKJAEVELAND S M, WHITSON C H. Two-phase pressure test analysis[J]. Spe Formation Evaluation, 1989, 4(4): 604-610.
[11] BEHMANESH H, HAMDI H, CLARKSON C R. Production data analysis of liquid rich shale gas condensate reservoir[J]. Journal of Natural Gas science and Engineering. 2015(22): 22-34.
Pressure and saturation relationship in CBM reservoir and the semi-analytical production forecast model for the horizontal well
ZHONG Ziyao, WU Xiaodong, HAN Guoqing
China University of Petroleum-Beijing, Beijing 102249, China
Coalbed Methane (CBM) reservoir numerical simulation is an effective tool for history match and production forecast of CBM horizontal wells, while the calculation methods of numerical model are often complex and require many input parameters. In order to get a simple and accuracy of production prediction method, the steady-state analytical productivity equation combined with unsteady boundary conditions can deduce a semi-analytical model of coalbed methane horizontal wells in linear fl ow. According to the numerical calculation results of CBM horizontal wells and the predecessors’ research, the relationship between saturation and pressure does not vary signif i cantly with time and space during transient fl ow and can be assumed to be unique for practical purposes. The corresponding approximate calculation of the water saturation can be made of formation pressure, and gas-water two phases pseudo-pressure can be obtained according to the relative permeability curve. The pressure and saturation calculation model arededuced in this paper based on the fl owing control equation of CBM, and the calculation method of water saturation by formation pressure is given. It provides a calculation basis for the gas-water two phase seepage model. Compared with the results of numerical method, and the history match of two horizontal wells in Qinshui Basin, the correctness and practicability of the semi-analytical model for CBM horizontal well is verif i ed.
CBM; two phases pseudo-pressure; production forecast; adsorption and desorption; two phases fl ow
10.3969/j.issn.2096-1693.2017.02.023
(编辑 马桂霞)
钟子尧, 吴晓东, 韩国庆. 煤层气水平井压力饱和度关系及半解析生产预测模型. 石油科学通报, 2017, 02: 251-257
ZHONG Ziyao, WU Xiaodong, HAN Guoqing. Pressure and saturation relationship in CBM reservoir and the semi-analytical production forecast model for the horizontal well. Petroleum Science Bulletin, 2017, 02: 251-257.doi:10.3969/j.issn.2096-1693.2017.02.023
*通信作者, wxd_308@163.com
2016-11-11
国家自然科学基金资助项目(51574256)资助
