基于响应曲面法某汽车前侧窗玻璃振动约束条件建模与分析
2017-06-28贺银芝石子豪
贺银芝,石子豪,吕 越
(1.同济大学 汽车学院,上海 201804;2.上海市地面交通工具空气动力与热环境模拟重点实验室,上海 201804)
基于响应曲面法某汽车前侧窗玻璃振动约束条件建模与分析
贺银芝1,2,石子豪1,2,吕 越1,2
(1.同济大学 汽车学院,上海 201804;2.上海市地面交通工具空气动力与热环境模拟重点实验室,上海 201804)
汽车行驶时,车内的气动噪声与侧窗玻璃的声振特性密切相关。不同的侧窗玻璃密封边界约束条件会导致其声振特性差别很大。因此对玻璃边界密封系统合理建模是研究以上问题的基础与前提。然而由于侧窗密封条的结构、变形问题复杂,直接建立真实的侧窗密封系统模型较困难。以某试验车左前侧窗系统为研究对象,根据功能等效原理以及密封条压缩线性假设,将侧窗密封条简化为矩形截面条状弹性体。利用响应曲面法与有限元方法,以试验结果的各阶固有频率为目标响应值,求解找到合适的矩形条等效刚度,建立简化模型。将仿真与试验结果进行对比,发现各阶振型吻合良好,证明该车型侧窗玻璃边界约束简化模型的可靠性。
振动与波;前侧窗玻璃;边界约束;密封条简化;响应曲面法
汽车行驶过程中,车内驾驶员耳旁的风噪声,与侧窗玻璃的声振特性密切相关[1]。车身周围气流分离形成的湍流压力脉动会激励侧窗玻璃振动,向车内辐射噪声。侧窗玻璃边界约束条件的不同会导致其振动特性差别很大。因此,研究侧窗玻璃的边界约束条件,并进行合理建模,可以为后续研究侧窗玻璃的声振特性奠定基础。
汽车车窗由密封条约束,它具有支撑车窗玻璃、提高车身密封性、防水防尘、隔声降噪等功能,结构形状与特性复杂。由于密封条大多使用超弹性橡胶材料,其约束具有几何非线性、材料非线性及边界条件非线性[2],因此车窗玻璃边界约束模型的建立较为困难。为了研究侧窗玻璃约束条件,便于后续工作的开展,需要将密封条进行等效简化处理。
国内外学者就侧窗密封条简化处理问题已进行了较多的相关研究。Francois Van Herpe等将侧窗密封条简化为截面为矩形的条状模型,计算车内的振动声学响应。但并没有给出具体简化过程以及对应等效模型参数[3]。Junhong Park等将密封条支承约束简化为黏弹性支承约束,研究了气流引起矩形平板振动的模型,并找到了能最大程度减小平板振动响应的最优支承刚度[4]。朱文峰等从功能等效原理出发,将侧窗密封条简化成弹簧的支撑约束,通过对比试验与仿真的玻璃系统在相同激励下的位移量,证明了所用方法的有效性[5]。
本文以某车型左前侧窗为研究对象,首先根据功能等效原理以及密封条压缩作用力-位移关系可以近似用一次函数表示的假设[6],将侧窗的密封条约束简化成矩形截面条状模型弹性约束。再利用响应曲面法与有限元方法,以弹性体等效刚度为设计变量,样本点仿真频率为响应值,构建响应曲面模型。以试验结果的前4阶固有频率为目标响应值,计算出最合适的等效刚度,建立等效简化模型。最后对比仿真与试验结果的各阶模态振型,发现等效简化约束模型与该车型侧窗密封系统约束效果相同,可作为下一步流固耦合情况下侧窗声振特性分析工作的基础边界条件。
1 侧窗玻璃系统模态试验
为获取某车前侧窗玻璃系统的结构动态特性,对真实约束条件下的前侧窗玻璃进行模态试验。首先在侧窗玻璃外表面合理布置测点。综合考虑试验效率以及试验结果的准确性,共布置了34个测点,如图1所示。
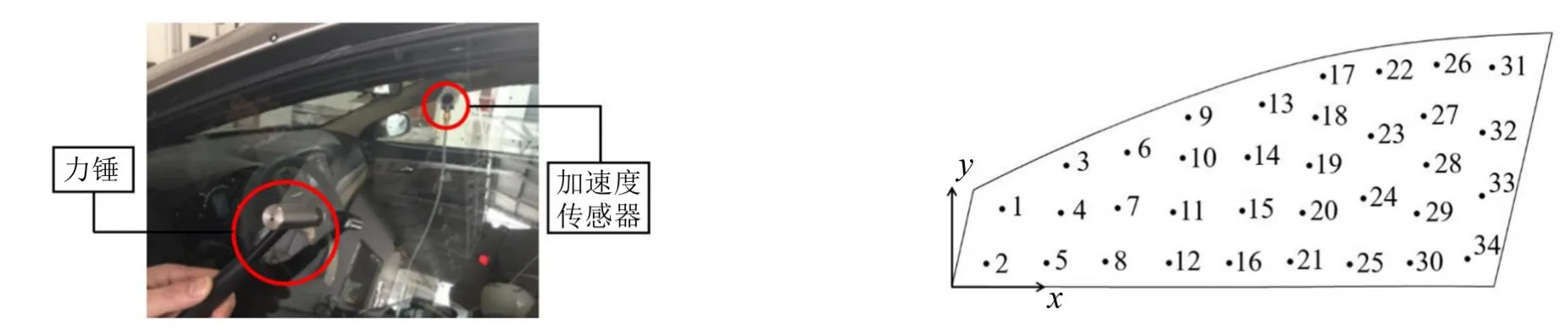
图1 侧窗系统模态试验及玻璃表面测点分布
试验应用锤击法,采用多点激励单点响应的方式,即在31点布置加速度传感器,依次用力锤激励所有测点,测得在不同位置激励下31点的加速度响应,从而获取一系列的传递函数。最后进行数据拟合,获得整个侧窗系统的前几阶固有频率以及对应的振型,为后续工作建立合理的目标响应值。本文列取前4阶的固有频率及模态振型,如表1、图2所示。

表1 侧窗系统前4阶试验固有频率
从试验结果所得模态振型可以看出,1阶固有频率下,侧窗玻璃绕着下方两个支撑销钉(图中未画出)进行前后摆动,类似于结构的刚体位移,但也有局部的变形。2阶固有频率下,侧窗玻璃绕着近似中线位置进行扭转变形。而3阶与4阶固有频率对应的振型则为弯扭组合变形。
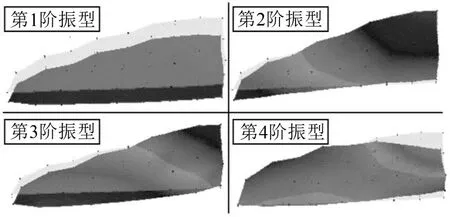
图2 侧窗系统前4阶试验模态振型
2 建立侧窗密封条等效简化模型
2.1 密封条的简化
图3为某车型侧窗密封条截面,它位于车门导槽内,结构比较复杂。在受到外力后,压缩变形过程存在弹性变形与塑性变形,具有非线性,直接建立真实模型进行分析计算比较困难。所以,可根据功能等效原理以及密封条压缩作用力-位移关系可以近似用一次函数表示的假设,将密封条支撑约束简化为弹性支撑约束。
如图4所示,将密封条简化为矩形条弹性体。通过简化处理,可忽略侧窗密封条的复杂形状,仅从密封条的作用效果来得到汽车侧窗玻璃边界约束条件。

图3 某车型侧窗玻璃密封条截面
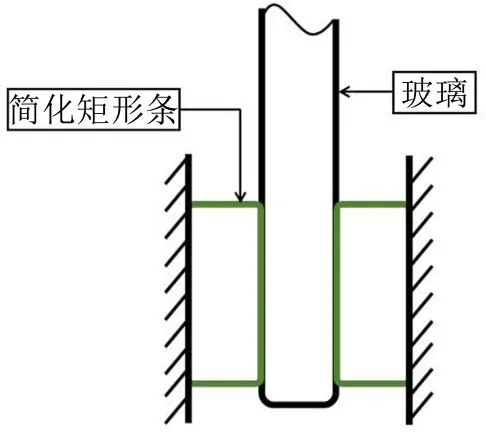
图4 密封条的简化模型截面
2.2 响应曲面法
响应曲面法是一种统计学试验设计方法,通过对给定的设计点集合进行试验,得到目标函数的响应曲面模型,来预测目标响应值对应的样本点[7]。模型关系式的一般表达形式为
波形PBL连接件试件的破坏形态表现为混凝土侧板首先出现裂缝,然后随着荷载的增加,裂缝开始至下向斜上方开展直至裂缝贯通,当裂缝到达顶部的时候又开始向连接件布置的位置延伸,当接近到极限荷载时,试件底部也开始出现混凝土压碎的现象.

式中C为统计误差,均值为0且满足正态分布;n为设计变量的个数。
响应面的近似函数通常使用2阶多项式,形式如下
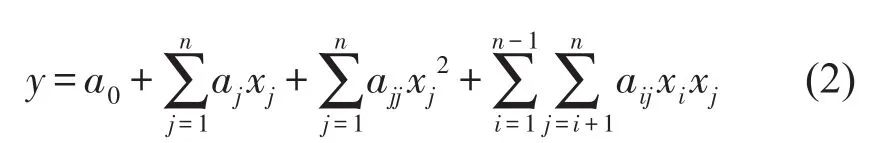
式中a为2阶多项式的系数,可通过最小二乘法计算得到。响应曲面法的具体过程如图5。
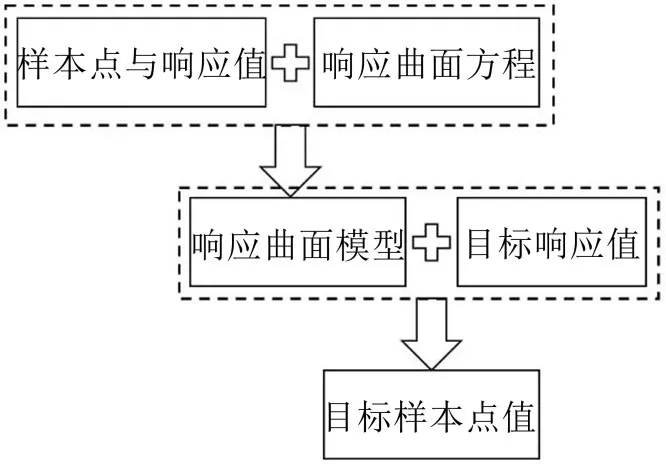
图5 响应曲面法流程
2.2.1 设计变量样本点的选取
样本点是响应曲面法计算中重要的初始参数,合理地选取样本点,可以有效减少样本点数量,并提高响应曲面的准确性。
优化空间填充法是样本点选取中常用的方法,它能保证样本点均匀地分布于样本空间中,在目标样本点位置不确定的情况下,能较快速且准确地寻找到目标值。如图6(a)为两个设计变量时的情况,样本点位置坐标为样本点的值。优化空间填充首先保证每个样本点与其他点在不同行,不同列的位置上。在此基础上,再调整样本点位置,使各个点之间的距离达到最大,均匀布满设计空间,如图6(b)。

图6 两变量优化空间填充法样本点分布
2.2.2 响应值的测量
响应值是响应曲面模型构造中的另一重要初始参数,其数值的准确性,将决定响应曲面模型的可靠性。
响应值有两种测量方法,试验法和有限元仿真法。试验法能够得到准确的数值,但是需要设计试验,适用于样本点少且模型简单的情况;有限元仿真法可以快速计算多样本点、复杂模型的响应值,但计算结果与真实值之间存在一定的误差。根据具体的情况选用合适的测量方法,可快速准确地获得响应值。
2.2.3 响应曲面模型评估
响应曲面生成后,需要对模型进行评估来确定其可靠性。一般用可决系数R2和均方根误差e来判断。它们的表达式如下。

式中n为设计变量个数;yi为第i个样本点的输出参数为第i个样本点的回归模型;为yi的算术平均值。
可决系数R2表示回归平方和在总变差中所占的百分比,可以作为综合度量回归模型对样本观测值拟合优度的度量指标,最优值为1。
均方根误差e表示样本点回归方法计算得到的数值与直接计算数值之间的误差,最优值为0。
2.3 建立等效简化模型
根据密封条压缩作用力-位移一次函数关系假设,密封条变形满足胡克定律,在外部载荷相同的情况下,等效刚度与变形量成反比关系。从图1可以看出侧窗边缘位置测点与密封条位置接近,为得到密封条各处的变形量,可用边缘测点的玻璃法向位移近似替代。
从试验振型可以知道,侧窗玻璃的1阶模态振型近似于刚体位移,玻璃自身变形量较小,密封条各位置受到的载荷差别较小,根据胡克定律,可以利用不同测点在1阶振型的位移量来探究等效刚度之间的关系。
将侧窗边缘位置测点划分为上下左右四个部分,图7为各部分测点位移-位置坐标曲线以及拟合曲线。从图中可以看出,各部分位移量线性度良好,且拟合曲线斜率接近于0,即同一部分各测点位移相等,则等效刚度也相等。所以,根据等效刚度的关系,可以将密封条简化成如图8所示的4个等效刚度未知的等效矩形条弹性体。
根据简化模型,建立如图9所示的有限元模型,有限元网格的尺寸为5 mm,各等效矩形条的外侧表面、玻璃下方的销钉孔内表面,均设置为固定支撑约束,与真实侧窗系统被约束的情况保持一致,图9深色框内为被约束位置。

图7 侧窗各部分测点位移-位置曲线及拟合曲线
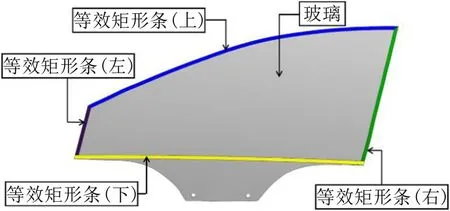
图8 前侧窗玻璃系统的简化模型

图9 前侧窗玻璃系统的有限元模型
将简化模型等效矩形条的等效刚度作为设计变量,样本点有限元仿真的前4阶固有频率作为响应值,试验测得的侧窗前4阶固有频率作为目标响应值,利用响应曲面法,得到目标样本点值,即等效矩形条的等效刚度,如表2。
采用两种方法验证响应曲面模型的可靠性:对模型进行评估,评估参数如表3,从表中可以看出各响应方程可决系数均达到最优值1,均方根误差接近最优值0;将响应曲面法得到的等效刚度参数代入有限元模型,仿真得到等效简化模型的前4阶固有频率,与试验测量值对比,如表4,发现二者之间的误差较小。两种方法均证明响应曲面模型可靠。

表2 各矩形条等效刚度

表3 响应曲面评估参数
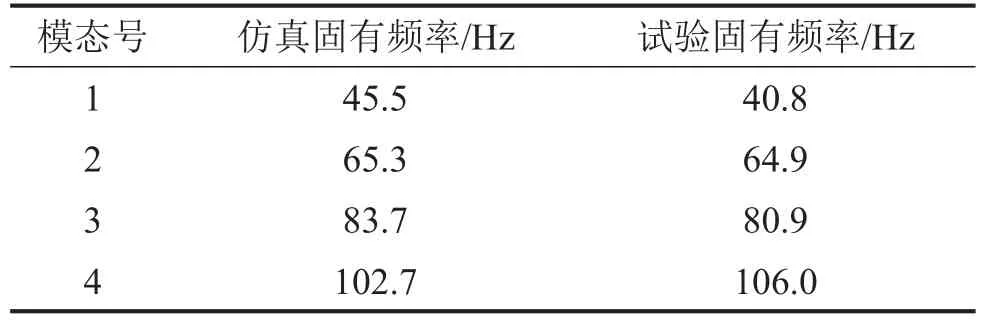
表4 仿真与试验固有频率对比
3 仿真与试验结果比较
通过上述方法,构建得到等效简化模型。为验证简化模型功能等效于此车型侧窗模型,将简化模型有限元仿真与实车侧窗模态试验的前4阶模态振型进行对比,如图9所示。

图9 侧窗系统试验(左)与仿真(右)前4阶振型对比
从试验及仿真模态振型的对比可以看出,各阶模态振型基本一致,验证了简化模型与此车侧窗密封系统作用效果相似,可作为下一步流固耦合情况下侧窗声振特性分析工作的基础边界模型。
4 结语
(1)根据功能等效原理以及密封条压缩线性假设,可以将某车侧窗密封条简化为矩形条弹性体。
(2)利用响应曲面法与有限元方法,以某车侧窗系统固有频率为响应目标值,可以较准确地计算得到矩形条弹性体的等效刚度,构建简化模型。通过对比仿真结果与试验数据,发现各阶固有频率下的模态振型吻合良好,证明了该玻璃约束边界条件简化模型的有效性,为下一步该车声振特性等相关问题的研究奠定了基础。
[1]NAOKI H,YASUHIKO O,KAZUO Y.Investigation for the effect of the external noise sources onto the interior aerodynamic noise[C].SAE paper,2013-01-1257.
[2]冯海星,高云凯.考虑压缩负荷的密封条传递损失分析[J].同济大学学报(自然科学版),2014,42(1):97-102.
[3]FRANCOIS V H,DIEGO D'U,JONATHAN J,et al. Vibro-acoustic simulation of side windows and windshield excited by realistic CFD turbulent flows including car cavity[C].SAE paper,2012-01-1521.
[4]JUNHONG P,THOMAS S,LUC M.Analysis of the flowinduced vibrations of viscoelastically supported rectangular plates[J].Journal of Sound and Vibration, 2003,(261):225-245.
[5]朱文峰,林佩剑,周辉,等.基于非线性刚度拟合的车窗系统约束分析与建模[J].机械工程学报,2015,51(20):171-176.
[6]朱文峰,林佩剑,周辉.高速流固耦合效应下车窗密封机理建模与分析[J].汽车工程,2015,37(12):1395-1399.
[7]熊俊涛,乔志德,韩忠华.响应面方法在跨声速翼型气动优化设计中的应用研究[J].西北工业大学学报,2006,24 (2):232-236.
[8]LIN C L.Robust design of glass run-channel seal[C].SAE paper,2004-01-1687.
[9]PARK J,MONGEAU L,SIEGMUND T.An investigation of the flow- induced sound and vibration of viscoelastically supported rectangular plates:experiments and modelverification[J].JournalofSoundand Vibration,2004,(275):249-265.
Modeling andAnalysis of Vibration Constraint Condition of Vehicle’s Front Side Window Glass Based on Response Surface Method
HE Yin-zhi1,2,SHI Zi-hao1,2,LYU Yue1,2
(1.School ofAutomotive Studies,Tongji University,Shanghai 201804,China; 2.Shanghai Key Lab of VehicleAerodynamics and Vehicle Thermal Management Systems, Shanghai 201804,China)
The aerodynamic noise in a travelling car is closely related to the vibro-acoustic characteristics of the side window glass.Different sealing constraint conditions of the side window glass can lead to great difference of the vibroacoustic characteristics.Hence,establishing a reliable and pertinent model for the boundary constraint condition of the front side window glass is the basis and precondition for the above mentioned problem.However,since the structure and deformation of the side window sealing are quite complex,it is difficult to directly establish its really practical model.In this paper,the front left side window of a sample car is studied.Based on the principle of functional equivalence and the assumption of linear Hooke’s law for the sealing in compression,the sealing is simplified as an elastic rod with rectangular cross sections.Using response surface optimization method and finite element method,and with the natural frequencies from the experiment as the target response values,the equivalent stiffness of the sealing is found and the simplified model is built. The results of the simulation agree well with those of experiment.The correctness and reliability of the simplified model for the boundary constraint condition of the side window are verified.
vibration and wave;front side window glass;boundary constraint;sealing simplification;response surface optimization
O327
:A
:10.3969/j.issn.1006-1355.2017.03.025
1006-1355(2017)03-0126-04
2017-03-07
国家自然科学基金资助项目(51575394)
贺银芝(1972-),女,安徽省砀山县人,副教授,研究方向为汽车噪声与振动控制、气动声学。
石子豪,男。E-mail:szh3483@163.com
