汽车发动机悬置系统多目标设计优化研究

张志强，徐 铁，陈丹华，蒋伟康

（1.上海交通大学 振动、冲击、噪声研究所机械系统与振动国家重点实验室，上海 200240；2.上汽通用五菱汽车股份有限公司，广西 柳州 545007）

汽车发动机悬置系统多目标设计优化研究

张志强1，徐 铁2，陈丹华2，蒋伟康1

（1.上海交通大学 振动、冲击、噪声研究所机械系统与振动国家重点实验室，上海 200240；2.上汽通用五菱汽车股份有限公司，广西 柳州 545007）

动力总成悬置系统对于汽车振动与噪声控制十分重要，通过考虑车身耦合因素，建立动力总成悬置系统十五自由度耦合模型，以扭矩轴解耦率和总传递振动力为综合优化目标进行优化，并将整车常用行驶工况考虑在内，以整车实测数据辨识出发动机激振力作为系统实际输入，应用粒子群算法对悬置系统刚度参数进行优化。计算表明选择合适的刚度参数可以有效降低汽车的传递振动力，并提高扭矩轴解耦率，从而改善汽车乘坐的舒适性。

振动与波；发动机悬置系统；舒适性；多目标优化；粒子群算法

近年来国内自主品牌汽车的市场占有率不断提升，但是在振动与噪声控制方面与国外高端产品相比还存在一定的差距。市场的激烈竞争使得以改善汽车乘坐舒适性为目的的汽车NVH的研究变得越来越重要[1]。发动机动力总成作为汽车行驶中的主要激励源，对驾驶员和乘客的舒适性及车辆运行的平顺度有着很重要的影响，因此，作为直接影响到汽车综合NVH性能的悬置系统，其优化设计具有非常实际的工程意义。

目前，对于汽车动力总成悬置系统的优化国内外学者做出了很多研究，一般可采用能量解耦法[2–3]、扭矩轴TRA（Torque Roll Axis）解耦法[4–7]以及振动响应或支反力最小[8]等方法进行优化设计，在应用能量解耦法时也可同时对悬置系统固有频率进行合理配置来进一步改善悬置系统隔振性能[9–10]。但是，上述设计方法常采用传统六自由度模型进行分析，忽略了与车身处的耦合，往往不能准确反映动力总成在整车下的实际振动情况[11]。采用能量解耦方法也具有一定的局限性，解耦率高也并不是隔振一定要追求的目标[12]。另外，由于动力总成绕曲轴线的倾覆力矩作用下产生的实际运动是绕扭矩轴的转动，因此考虑在扭矩轴坐标系的能量解耦更具有实际意义[7]，但国内有关研究相对较少。同时，汽车动力总成不同布置方式与传动系统多样性等条件也对动力总成悬置系统优化提出了不同的设计要求[13]，而在悬置系统优化设计中，常采用模拟激励作为动力总成的激振力输入，考虑到不同的动力传动系统等因素，使得上述方法在应用时不一定能满足优化设计要求。

因此，本文以某国产直列四缸发动机汽车为例，将车身耦合因素考虑在内，建立了动力总成悬置系统耦合模型，并推导出了动力总成传递到车身传递力表达式。同时，以整车测试为基础辨识出了汽车行驶工况下的实际发动机激振力。在扭矩轴坐标系下建立动力学方程，以扭矩轴能量解耦率和总传递振动力作为综合优化目标函数，对发动机动力总成悬置系统进行多目标优化设计。

扭矩轴能量解耦率可对动力总成系统耦合度进行约束，传递振动力可将动力总成与车身耦合考虑在内。经过优化后，与初始系统相比，动力总成传递到驾驶室座椅处的振动力有了很大的改善，同时能量解耦率增大，提高了悬置系统的隔振降噪性能。

1 系统力学模型

1.1 动力总成悬置系统耦合模型

本文中研究对象采用三个悬置，为了考虑动力总成和车身的耦合，此处将悬置安装点视为弹性节点，以该三个弹性节点之间的导纳函数来代表车身的动特性[14]。动力总成悬置系统简化模型如图1所示。采用拉格朗日方法可得到系统的振动微分方程。简化模型中总计十五个自由度（动力总成六个自由度，左、右和后悬置处的三个弹性节点共九个自由度）。

图1 动力总成-悬置系统简化模型

以动力总成的质心坐标系O-XYZ为标准，三个悬置点处的局部坐标系的坐标轴见图1所示。设广义坐标为qe=[q0q1]T，其中表示动力总成的位移矢量，表示左悬置、右悬置、后悬置与车架三个弹性节点的位移矢量。

不考虑阻尼时，系统振动微分方程可描述为

式（1）中Me、Ke分别是系统质量矩阵和刚度矩阵，可以由系统动能表达式和系统势能表达式推导而来。是激振力矢量。

质量矩阵表达式如下

其中m为动力总成质量，I为动力总成的各个转动惯量和惯性积。

刚度矩阵可表示为

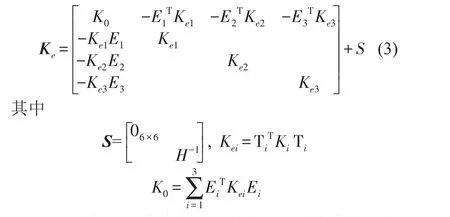
H可以由力锤敲击实验测得。Ei表示动力总成刚体质心的运动引起刚体上悬置点三个方向运动的位移转移矩阵。Ti矩阵表示夹角欧拉旋转矩阵。Ki表示第i个悬置在局部坐标系下的三个方向的刚度组成的刚度系数矩阵。

1.26自由度模型

解耦率是悬置系统的重要特性，由于动力总成固有频率一般低于30 Hz，将动力总成悬置系统简化为一个空间六自由度系统。

动力总成悬置系统只包含q0的6个自由度，在扭矩轴坐标系下，其运动微分方程为

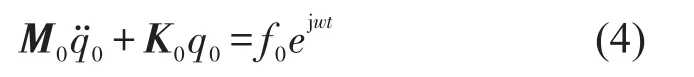
该系统一般可采用发动机曲轴坐标系CXYZ、主惯性轴坐标系CXPYPZP和动力总成扭矩轴坐标系CXTYTZT表示，如图2所示，这三种坐标系相互关联，各坐标系可进行相互转换，可通过欧拉角来表达。

考虑到动力总成在绕曲轴线的倾覆力矩作用下产生的实际运动是绕扭矩轴的转动，因此选取扭矩轴能量解耦率作为优化目标之一。

2 激励

2.1 激励分析

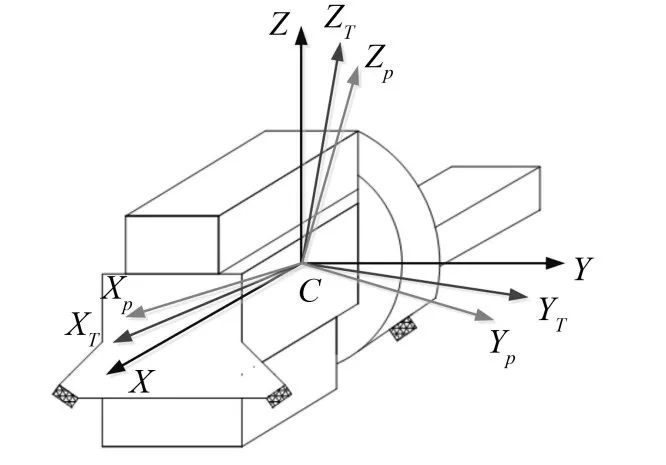
图2 动力总成相关坐标系

汽车在行驶过程中激励主要来源来自于发动机动力总成和路面激励。路面激励一般频率较低，而且由于我国路面平整度的提升，使得汽车悬置系统优化时需要着重考虑发动机动力总成的激励影响因素。

由于本文研究对象为直列四缸发动机，悬置承受的静态力一般包括动力总成的重力和发动机输出扭矩的反力，对于该四缸四冲程发动机，低频区的激振力成分主要是第2、4阶扭矩谐量，第2阶不平衡往复惯性力则是中高频区主要激振来源[13]。发动机点火脉冲频率为

其中n为发动机转速，i为发动机汽缸数，τ为发动机冲程数，对于怠速工况，由于发动机转速为750 r/min，点火脉冲频率为25 Hz，考虑到隔振原理，因此在考虑悬置系统优化时需要对频率进行相应约束以满足隔振要求。

同时，汽车动力传动系统多样性和发动机不同的布置方式等原因都会引起激励主要影响因素的变化，因此，在对悬置系统进行优化设计时，辨识出实际发动机激振力便显得尤为重要。

2.2 激振力

由上述激振讨论可知，由于不同传动方式和布置方式等都会使激励发生很大变化，因此，本文中采用整车测试方法，通过悬置处的加速度响应测试来辨识发动机实际激振力大小。

激振力辨识方程表达式如下

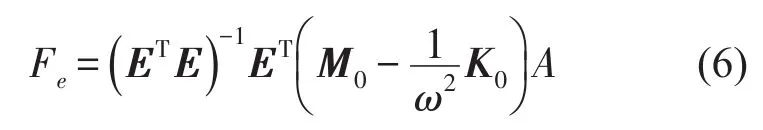
其中E=[E1E2E3]T是位移转移矩阵。A是悬置点处的加速度响应。

同时，测试中将整车行驶常见工况均考虑在内，包括怠速和常用档位与速度下的行驶工况，测试工况选择见表1所示。

表1 辨识工况/(km∙h-1)

通过整车测试，可以辨识出各个工况下的实际运行中的动力总成等效激振力。

此处，以怠速工况为例，整车测试辨识结果见图3和图4所示。

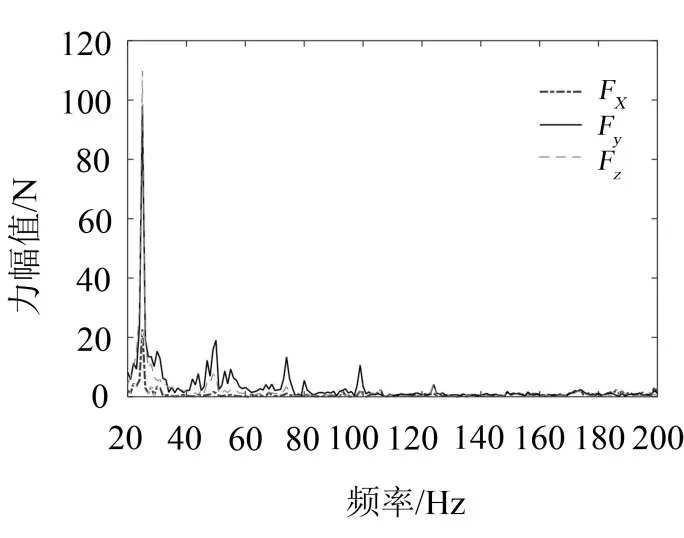
图3 力辨识结果

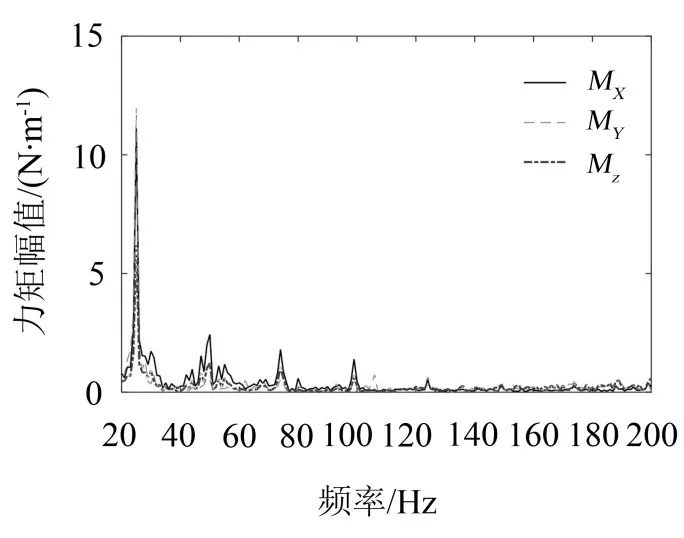
图4 力矩辨识结果

3 综合目标悬置优化

3.1 扭矩轴坐标系下的能量解耦

对动力总成悬置系统进行固有特性分析，可将振动系统简化为一个无阻尼的自由振动系统，根据质量矩阵M0和振型矩阵K0，可很方便得到系统在做各阶振动时的能量分布，能量分布计算公式如下

其中Tq反映了各阶模态的耦合程度分别为系统第i阶主振型的第l个元素和第k个元素，mkl为系统质量矩阵的第k行、第l列元素。

由于本文中的研究对象发动机采用四缸四冲程发动机，解耦率要求越高越好，使得当发动机在扭矩轴方向能够尽可能完全解耦。

3.2 传递振动力

由测试辨识出的发动机激振力辨识结果Fe和振动微分方程，可求得悬置处的支反力稳态响应为F(f)。

定义FM为总传递振动力，则

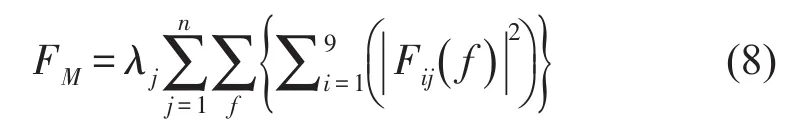
其中λj为各工况下的加权因子，Fij是第j个工况下对应的悬置支反力稳态响应结果。根据帕塞瓦尔定理，考虑到系统的实际振动响应，选取20 Hz～200 Hz频带范围，同时，为了将汽车常见工况全部考虑在内，定义每个工况下的传递振动力比率为

其中FM前与FM后分别是初始系统参数和优化后刚度参数所得到的传递振动力值。

3.3 综合优化

为了综合考虑解耦率与传递振动力要求，选取解耦率与传递振动力比率τj为变量，由于解耦率Tq本身就具有的取值范围，此处对振动力比率作归一化处理，使得各参数均满足0到1的取值，可使得算法更加稳定有效。

其中Aj和aj是所允许的最大值与最小值，因此最终选取的目标函数为

其中βj与γi为相应的加权因子

4 优化实例

由于该型汽车已经量产，因此优化中不改变悬置安装位置与角度，只选取悬置的刚度参数进行优化设计。

约束条件：对刚度进行约束，保证悬置刚度不会太软和太硬；对刚度剪切比进行约束，为了制造方便，本文中左悬置和右悬置橡胶的刚度剪切比设定为3～8之间；固有频率约束，考虑到当激励频率大于倍的系统固有频率时，系统才能起到隔振作用。因此选取频率：5 Hz≤f≤20 Hz，同时考虑到相邻两阶固有频率不能靠得太近。

优化算法使用粒子群优化算法[6]，粒子群优化算法是一种基于迭代的优化求解算法，系统初始化生成一组随机解，然后通过一定的机制迭代直到收敛得到最优解。优化后，初始系统和优化后刚度参数见表2所示。

表2 悬置系统优化前后刚度对比/(N∙mm-1)

将优化前初始系统和优化后系统作对比，结果见图5和图6所示。由图可知，经过优化后的系统，动力总成传递到主驾驶座椅处的加速度响应有了很大的降低，共降低2.2 dB左右，优化效果明显。

同时，通过观察可知，在汽车行驶常用工况下，各频带的传递振动力幅值均有了一定程度的降低，优化结果对于全频带和各工况均有效，优化过程具有一定的普遍意义。

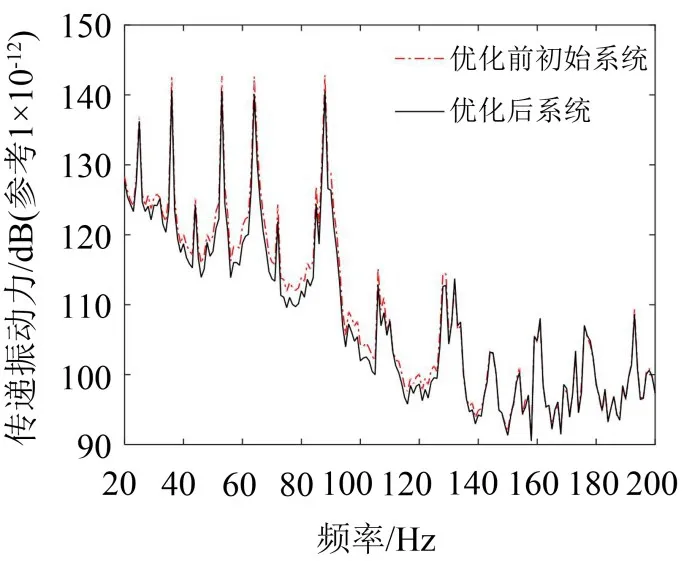
图5 优化前后传递振动力对比

图6 优化前后传递振动力1/3倍频结果对比

根据扭矩轴坐标系下能量解耦方法，初始系统的能量分布和模态频率见表3所示。优化后能量分布参数见表4所示。

通过表3和表4中优化前后悬置系统能量分布对比，可知在扭矩轴坐标系中，TRA轴方向能量解耦率有了很大的改善。

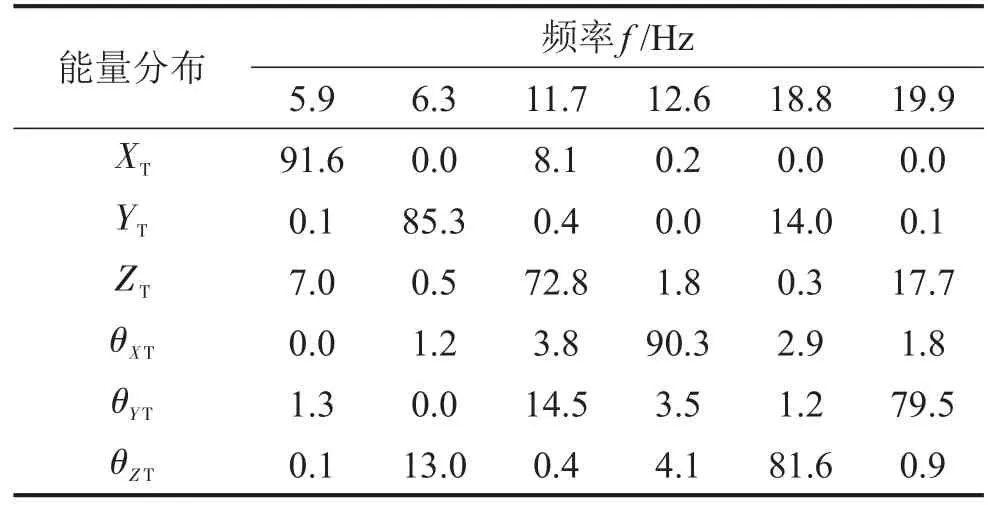
表3 初始系统的解耦率/(%)

5 结语

本文选取某型四缸直列发动机汽车为研究对象，对动力总成悬置系统进行了综合目标优化，主要研究内容及结论如下：

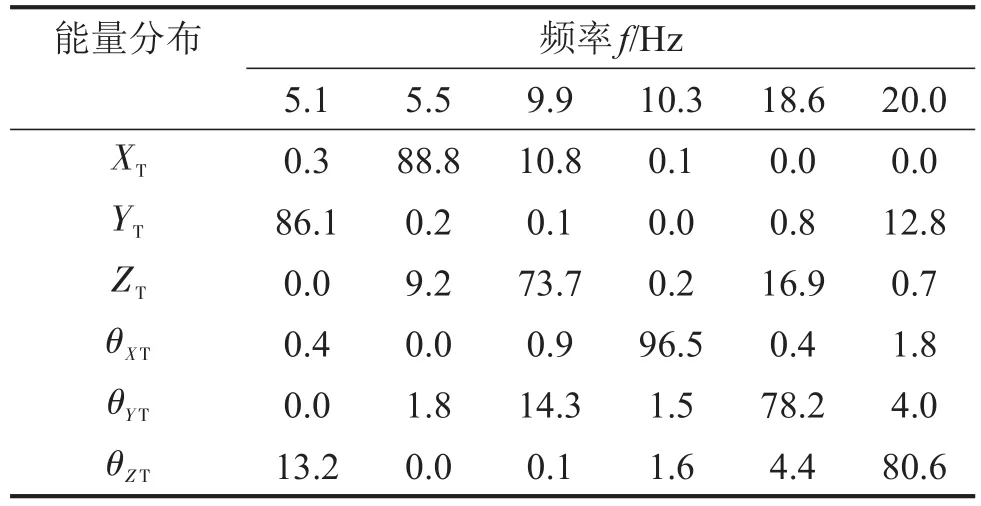
表4 优化后系统的解耦率/(%)

（1）建立了发动机动力总成悬置系统十五自由度耦合模型，与传统六自由度振动模型相比可以考虑车身弹性因素影响，并推导出了动力总成传递到车身的全工况总传递振动力。

（2）通过整车测试辨识出汽车各运行工况下发动机的等效激振力，辨识过程不限汽车传动方式和发动机布置方式的影响，可以作为悬置系统优化设计中的实际激振力输入，与模拟激励输入相比更加接近实际情况。

（3）阐述了悬置系统在扭矩轴坐标系下的解耦理论，应用粒子群优化算法对总传递振动力和扭矩轴能量解耦率进行综合优化。优化结果表明总传递振动力有了明显降低，且扭矩轴能量解耦率有很大改善，可以满足优化目标要求，结果表明该方法可有效提高汽车乘坐舒适性与悬置系统隔振性能。

[1]林逸，马天飞，姚为民，等.汽车NVH特性研究综述[J].汽车工程，2002，24(3)：177-181.

[2]SEONHO CHO.Configuration and sizing design optimisation of powertrain mounting systems[J].International Journal of Vehicle Design,2000,24(1):34-

Multi-object Optimization of Vehicle Engine Mounting Systems

ZHANG Zhi-qiang1,XU Tie2,CHEN Dan-hua2,JIANG Wei-kang1
(1.Institute of Vibration Shock&Noise,State Key Laboratory of Mechanical System and Vibration, Shanghai Jiaotong University,Shanghai 200240,China; 2.SAIC GM WulingAutomobile Co.Ltd.,Liuzhou 545007,Guangxi China)

Engine mounting system is very important for automobile vibration and noise control.In this paper,a 15-DOF vehicle’s body and the powertrain mounting system coupled model is established.With the decoupling rate of the torque shaft and the total transferred vibration force as the objective functions,the whole vehicle structure is optimized considering the common driving conditions.The particle swarm optimization(PSO)algorithm is used to optimize the mounting stiffness parameters with the use of the identified excitation forces as the actual force input.The results show that choosing proper stiffness parameters of the mounting system can effectively reduce the transferred vibration force and increase the decoupling rate of the torque shaft so that the comfort of the automobiles can be improved.

vibration and wave;engine mounting system;comfort;multi-object optimization;particle swarm optimization algorithm

TB53；U461.4

：A

：10.3969/j.issn.1006-1355.2017.03.023

1006-1355(2017)03-0117-04

2017-02-21

张志强（1990－），男，河南省周口市人，硕士生，主要研究方向为汽车NVH。

蒋伟康，男，博士生导师。E-mail:wkjiang@sjtu.edu.cn