阻燃涤纶/芳纶/聚苯丙噁唑纤维三轴系复合纱的拉伸性能

房家惠， 于伟东,2

(1. 东华大学 纺织学院， 上海 201620； 2. 东华大学 纺织面料技术教育部重点实验室， 上海 201620)

阻燃涤纶/芳纶/聚苯丙噁唑纤维三轴系复合纱的拉伸性能

房家惠1， 于伟东1,2

(1. 东华大学 纺织学院， 上海 201620； 2. 东华大学 纺织面料技术教育部重点实验室， 上海 201620)

针对多组分纱线拉伸力学行为的理论模型描述不准确问题，以Vangheluwe模型为基础，对三轴系高性能复合纱的拉伸行为进行分析。Vangheluwe模型不适合描述准线形类纤维，对Vangheluwe模型在应变为零时弹簧模量为零的缺点作修正，得到修正模型。同时，结合Jacobian矩阵与Hessian矩阵在非线性最小二乘法中的应用，用MatLab对非线性回归方程进行求解，拟合优度值达到0.999 86，修正后模型的物理意义更准确、表征精度更高。此外，还选用单元件非线性弹簧模型和单元件线性弹簧模型对上述复合纱线拉伸行为进行描述。结果表明，2种模型与该复合纱的实测值拟合亦很好，拟合优度值分别为0.999 85和0.988 04，其中单元件线性弹簧模型可对复合纱拉伸过程的平均模量进行表征。

复合纱； 拉伸性能； 非线性三元件模型； 应力-应变方程

作为防火耐高温、防高光热辐射的高性能乃至智能织物，其构成单元——纱线是织物性能与功效实现的重要组成部分。而如何在选定阻燃及高性能纤维的条件下，获得高效阻燃并具备高强的纱线，是涉及纱线中纤维分布排列和等模量应变的问题，需要借助理论建模表征和实验验证。已有学者基于弹簧与黏壶的串并联模型来表征复合纱线的拉伸行为，但大都限于天然纤维和常见化纤的二组分或三组分混纺及复合纺纱[1]。

早在1992年，比利时学者Vangheluwe[1]提出了用一个非线性弹簧与Maxwell模型并联，该非线性弹簧的本构关系为σ=bε2(σ为应力；ε为应变；b为待求参数)。樊理山等[2]用七元件对涤纶/棉/涤纶长丝三组分复合纱线的拉伸断裂特征与力学模型进行了表征，其中弹簧选用的是线性弹簧，结果与实际基本符合，但元件数太多，其中引入2个滑块杆件以表示复合纱线某组分一种临界状态时所受力状况，本质上为单线性弹簧与双Maxwell模型并联模型(五元件)，虽选用的弹簧均为线性弹簧，但是模型繁杂性较大。高小平等[3]选用了Vangheluwe模型以及Maxwell模型与线性弹簧并联的三元件模型对聚丙烯纱线力学性质中的黏弹性进行了分析，且因不会解松弛方程而仅分析了2种模型的蠕变方程，并得到Vangheluwe模型的更优的结果。吕立斌等[4]选用线性弹簧并联Vangheluwe模型(四元件)对涤/棉/丝三组分Sirofil复合纱的拉伸性能进行分析；Shi等[5]用同样的四元件模型对莫代尔/聚氨酯包芯纱线的拉伸特性做出了表征，虽表述不同，但实质上是一致的，是对Vangheluwe模型进行修正，将非线性方程部分的σ=bε2修正为σ=bε2+E3ε，其中E3为线性弹簧的模量。由于方程解法较为困难，为简化计算，2组作者均将自然指数部分处理后，将方程简单化为多项式函数，表达式为：σ=σ0+α1ε+α2ε2+α3ε3+α4ε4+Λ，其中Λ表示无穷小项；α1、α2、α3、α4均为常数，通过多项式回归计算得出回归方程，对改进后模型的解法来说，在简化方程中的高次项，已失去经典物理意义及量纲。

高模量高强纤维在力学性质上有较好的线弹性且塑性小，本文选用经典的Vangheluwe模型讨论其与阻燃涤纶/芳纶/聚苯丙噁唑(聚-p-亚苯丙二噁唑，PBO纤维)高性能纤维纱线拉伸行为的一致性及对模型进行修正，使其更加精简化，即选用三元件模型，并选用新的求解方法，找到适用于该类纱线的精确模型。

1 实验部分

采用山东沃源新型面料股份有限公司提供的18.4 tex的阻燃涤纶/芳纶/PBO三纤维束，将其同时喂入前罗拉钳口加捻成形，得到三轴系复合纱。其中阻燃涤纶纤维、芳纶纤维、PBO 纤维的拉伸测试，根据GB/T 14337—2008《化学纤维、短纤维拉伸性能试验方法》进行。三者的复合纱线的测试根据GB/T 3916—2013《单根纱线断裂强力和断裂伸长率的测定》进行。

纤维和纱线的测试仪器分别选用LLY-06E型纤维拉伸试验仪以及YG061-1500型单纱拉伸试验仪。以上实验均在恒温恒湿(温度为20 ℃，湿度为65%)条件下进行，试验参数如表1所示，在相同试验条件下测试200次，得到平均强力、伸长率以及平均拉伸曲线。

表1 实验参数设置

2 高性能复合纱力学模型的讨论

2.1 2种非线性三元件模型

图1示出实测的PBO纤维、芳纶(对位)纤维、阻燃涤纶纤维的拉伸曲线。由图1可知，3种纤维均为高模量和屈服点明显的纤维，且屈服点前的高模线性段的长度为：PBO纤维>芳纶>阻燃涤纶。

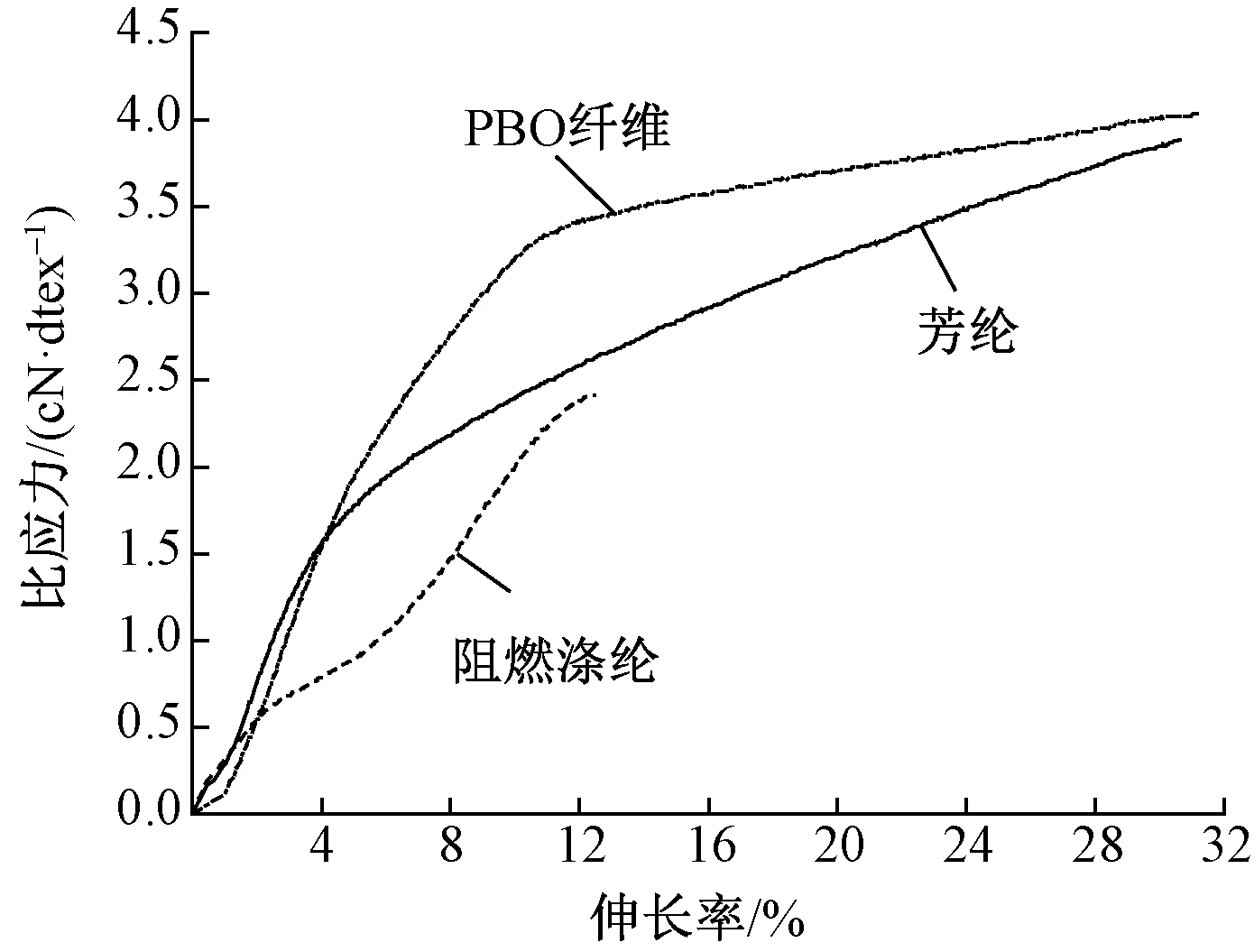
图1 PBO、芳纶和阻燃涤纶的拉伸曲线Fig.1 Tensile curves of PBO fiber, aramid fiber and flame retardant polyester

其中PBO和芳纶的拉伸曲线在屈服点后有较长的屈服平台区(post-yield region, PYR)，选择非线性弹簧表示；对于阻燃涤纶来说不仅存在屈服平台区(PYR)，而且有显著的强化区(strengthen region)，即模量重新上升的阶段，故阻燃涤纶的模量非线性及复杂性是显而易见的。因此，选用Maxwell模型与非线性的弹簧E2=bε2并联的Vangheluwe模型(非线性弹簧三元件模型)结果，对阻燃涤纶/芳纶/PBO三轴系复合纱的拉伸行为进行表征。

图2示出模型ⅠVangheluwe模型与模型Ⅱ(修正Vangheluwe模型)的物理元件构成。其中：E1为线性弹簧的模量；η为牛顿黏滞系数，以上参数根据上述三轴系复合纱实测值确定；b，c为待求参数。

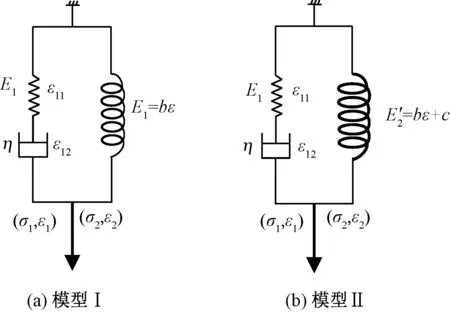
图2 模型Ⅰ与模型Ⅱ示意图Fig.2 Schematic diagram of model Ⅰ (a) and model Ⅱ (b)

模型Ⅰ(Vangheluwe模型)的本构方程，可由Maxwell模型与非线性弹簧并联关系可得：

(1)

(2)

解一元线性非齐次方程，解得模型Ⅰ的应力与应变方程为

(3)

式中v为速度。

当t=0时，即

(4)

由于是等速伸长(CRL)模式，

(5)

(6)

由此可知，Vangheluwe模型在ε=0时，非线性弹簧的模量E20=bε=0，即三元件模型表现出Maxwell二元件模型的特征，这与实际不符。

因此，对Vangheluwe模型中的非线性弹簧进行修正，令：

(7)

(8)

(9)

(10)

(11)

(12)

2.2 模型参数求解与实测曲线对比

本文采用非线性最小二乘法来估计非线性模型Ⅰ和模型Ⅱ各有的参数[6]。

残留函数ri(ε)=σi-f(εi,ε)，(i=1,2,…,m)，则非线性最小二乘法的问题为函数σ(ε)=r(ε)Tr(ε)的最小化问题F(ε)在εk处的泰勒展开为：

(13)

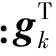
因此，步长△εk可通过解关于r(εk)的Jacobian矩阵和r(εk)的Hessian矩阵的线性方程求解：

(14)

本文结合Jacobian矩阵与Hessian矩阵在非线性最小二乘法中的应用[7]，基于MatLab对方程进行非线性回归方程参数计算[8]，得到相关参数以及残差数如表2所示。

表2 模型Ⅰ与模型Ⅱ回归方程参数估计值

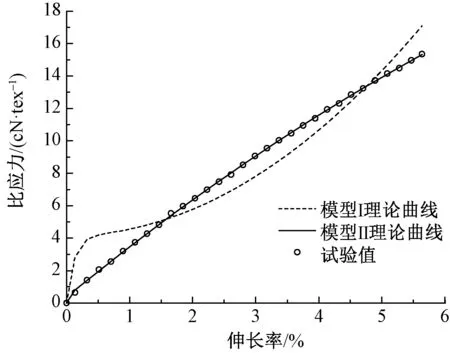
图3 模型Ⅰ和模型Ⅱ理论曲线与实验值Fig.3 Model Ⅰ and model Ⅱ fitted curves andexperimental data for yarn

模型Ⅰ和模型Ⅱ的非线性回归方程如式(15)和式(16)所示。显然，Vangheluwe模型更适用于羊毛类纤维，即有明显线性弹性初始区，明显的屈曲点和屈服区以及最后的强化区三区段。

(15)

修正后的Vangheluwe模型是上凸的非线性曲线，很接近于线性，这符合高性能纤维的拉伸性为。

2.3 2种单弹簧模型的拟合

依据实测三轴系纱线的曲线特征可知，用更为简单的弹簧，即单个非线性弹簧模型a，或直接近似为线性弹簧的模型b，可精准地表述三轴系纱线的拉伸行为。2种单弹簧的模型a与模型b的应力与应变方程如式(17)～(18)所示，2种弹簧元件如图4所示。

图4 模型a与模型b示意图Fig.4 Schematic diagram of model a and model b. (a) Nonlinear spring model; (b) Linear spring model

对模型a的非线性回归方程参数计算原理同模型Ⅰ与模型Ⅱ的参数计算原理一致，得到模型a的相关参数以及残差数据，如表3所示。

表3 模型a回归方程参数估计值

(17)

(18)

(19)

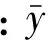
试验值散点曲线与模型a和模型b的对比如图5所示。模型a非线性回归方程如式(20)所示。模型b的线性回归方程如式(21)所示。

图5 模型a模型b理论曲线与实验值Fig.5 Model a and model b fitted curves and experimental data for yarn

(20)

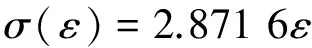
(21)

正因为芳纶与PBO 纤维的近似线性的拉伸曲线，所以用一个弹性为主的非线性弹簧即可，虽然模型a并无实际的物理意义，但对于幂指数的次数的选取有着借鉴意义，其幂指数接近1。

线性弹簧模型b表示三轴系纱线的模量是不随拉伸而变化的，是对于整个拉伸过程中的模量的平均值的一个描述。

3 结 论

Vangheluwe有着明显线性弹性初始区，屈服区和最后的强化区的特征，并有明确的屈服点，但是实测三轴系复合纱却不存在，故用Vangheluwe模型来描述三轴系高性能复合纱的拉伸行为是不合适的，即Vangheluwe模型不适合描述准线形类纤维，而更适于对羊毛类纤维的描述。

虽然阻燃涤纶在单独拉伸状态下有黏弹性的性质，但是在复合后，复合纱的拉伸性质并没有表现出明显的黏流区，而仅表现出模量的略微减少趋势，是因为3种纤维都存在屈服的塑性变形所致，尤其是PBO纤维与芳纶。

修正的Vangheluwe模型和单个非线性弹簧模型理论值与实测值均拟合较好，其各自的拟合优度值均达到0.999 8以上。修正的Vangheluwe模型更有优势，不仅物理概念明确，还可式解。2个弹簧模型a和模型b虽拟合精度高，但只是数值上的吻合，物理意义不明确，故认为采用修正后的三元件模型是实用、精确的，对复合纱黏弹性表达更完整。

FZXB

[ 1] VANGHELUWE L. Influence of strain rate and yarn number on tensile test results[J]. Textile Research Journal, 1992, 62(10):586-589

[ 2] 樊理山,来侃,孙润军,等. 三组分复合纱线的拉伸断裂特征与力学模型[J]. 纺织学报, 2010(3):36-39. FAN Lishan, LAI Kan, SUN Runjun, et al. Tensile strength of tri-component composite yarn and its mechanical model [J]. Journal of Textile Research, 2010(3):36-39.

[ 3] GAO Xiaoping, SUN Yize, MENG Zhuo, et al. Analytical approach of mechanical behavior of carpet yarn by mechanical models[J]. Materials Letters,2011, 65: 2228-2230.

[ 4] 吕立斌，杜梅，赵磊.涤棉丝Sirofil复合纱的拉伸性能分析[J].纺织学报,2007,28(6)：45-46. LÜ Libin, DU Mei, ZHAO Lei. Tensile properties analysis of polyester/cotton/silk tri-component Sirofil composite yarn[J]. Journal of Textile Research, 2007,28(6)：45-46.

[ 5] SHI F, JIN X. Modelling the tensile properties of modal/polyurethane core-spun stretch yarn[J]. Fibres and Textiles in Eastern Europe,2012,92(3):30-32

[ 6] MA Xiaofang, FUNG Richard Ying Kit, XU Chengxian. Stable factorized quasi-Newton methods for nonlinear least-squares problems[J]. Journal of Computational & Applied Mathematics, 2001, 129(1/2):1-5.

[ 7] MIZUTANI E, DEMMEL J W. On sparsity-exploiting memory-efficient trust-region regularized nonlinear least squares algorithms for neural-network learning[J]. Neural Networks, 2003(1):242-247.

[ 8] EL-SHEHAWY S A. On calculating the hougaard measure of skewness in a nonlinear regression model with two parameters[J]. Journal of Mathematics and Statistics, 2009, 5(4):360-364.

[ 9] DURSUN Aydan. A comparison of the sum of squares in linear and partial linear regression models [J]. International Journal of Mathematical, Computational, Physical, Electrical and Computer Engineering, 2008,506(32)：476-482.

[10] DU Yuhong, LUO Yongheng, JIANG Xiuming, et al. Research of foreign fibers in cotton yarn defect model based on regression analysis[J].The Journal of the Textile Institute,2016,107(9)：1089-1095.

Mechanical analysis of flame retardant three-strand yarn of polyester/ aramid fiber/poly(p-phenylene-2,6-benzo-bisoxazole) fiber

FANG Jiahui1, YU Weidong1,2

(1.CollegeofTextiles,DonghuaUniversity,Shanghai201620,China; 2.KeyLaboratoryofTextileScience&Technology,MinistryofEducation,DonghuaUniversity,Shanghai201620,China)

Aiming at the problem of inaccurate description of the theoretical model of the tensile mechanical behaviors of multi-component yarns, based on the Vangheluwe model, the tensile behavior of three-strand high performance composite yarn was analyzed, but the tensile behavior of three-strand high performance composite yarn is not suitable for describing quasi-linear fiber, and the major disadvantage of the Vangheluwe model, however, is modified, that is, elastic modulus is equal to zero without strain to obtain a modified model accordingly. Taking the application of Jacobian matrix and Hessian matrix in nonlinear least square method (LSM) into consideration, the nonlinear regression equation was solved by MatLab, and the goodness of fit value reached 0.999 86. The physical meaning of the modified model was more precise, moreover, the accuracy of which was higher. In addition, one element model of the nonlinear and linear spring model was also employed to describe the tensile behavior of composite yarns. The results show that the two models has good fitting with the measured values of the composite yarns, and the theoretical analytic results on goodness of fit value present at 0.999 85 and 0.988 04. Finally, the linear spring model of the element proposed can be used to characterize the average modulus of the tensile process of the composite yarns.

composite yarn; tensile property; nonlinear three elements model; stress-strain equation

10.13475/j.fzxb.20160608105

2016-06-30

2017-01-06

房家惠(1992—)，女，硕士生。主要研究方向为阻燃纱线的力学建模。于伟东，通信作者，E-mail: wdyu@dhu.edu.cn。

TS 104.1

A