基于AR(n)模型的网络带宽流量动态分配预测算法研究

赵明

(天津交通职业学院， 天津 300110)

基于AR(n)模型的网络带宽流量动态分配预测算法研究

赵明

(天津交通职业学院， 天津 300110)

网络突发式的流量变化已经逐步取代平稳的语音服务，需要网络能够动态预测和调整流量分配。AR(n)模型作为网络流量预测中常用算法，相比于自相似模型其预测的精度稍有不足，但在计算性能上表现较好，以粒子群算法对AR(n)模型进行预测精度调优，采用AIC准则判断模型的最佳阶数。通过实验比较研究了最小二乘、灰色理论估计和自相似模型在预测精度和计算性能上差异性，实验结果表明，基于粒子群的AR(n)模型具有较好的预测精度。

AR(n)模型； 流量预测； AIC准则； 粒子群算法； 预测精度

0 引言

数据快速增长使得网络流量发生非常明显的变化，传统的基于语音传输的稳定流量网络已经逐渐退出主流舞台，取而代之的是网络流量趋于动态变化的突发式网络状态[1]。通常而言，网络流量的变化具有一定的不确定性，因为受到多种因素的制约和影响，每个因素都可能导致流量的激增或变化[2][3]。在一定程度上，网络数据的传输依赖带宽资源，带宽在传输介质固定的情况下较为稳定不易发生改变，因此在网络带宽固定的情况下如何动态的调配网络流量的分配至关重要[4]。

网络带宽的流量动态分配需要根据当前网络的数据传输和网络通道数据量进行动态调整，保证数据传输的最大效率和最低时延[5]。研究表明，网络流量的特性符合自相似分布，表现为网络流量在不同时间尺度上具有相似的突变尺度，具有长相关性的数据统计规律。针对长相关性的网络流量预测分为两个方向：基于时序模型和自相似模型[6]。基于自相似模型通常能够获得较高的预测精度，但存在运算复杂度过高的缺陷，难以满足在网络传输过程中快速高效预测运算的要求[7][8]。本文主要针对基于时序的AR(n)模型预测精度不足的问题，采用粒子群算法对模型阶数进行优化训练，粒子群算法作为一种全局优化算法，在AR(n)模型的阶数训练过程中通过粒子群算法迭代预测误差，当预测误差达到设定终止条件则定义当前的阶数为最佳阶数。

1 AR(n)模型

AR(n)模型将自相似网络的流量预测通过差值运算或者对数变换转换为平稳的时间序列预测，时间序列的预测可以通过成熟的数学模型实现[9]。一般情况下，大时间范围内的时间序列预测的准确性要优于短时间范围内的时间序列预测。AR(n)模型的时间序列预测通过对历史时间片段的数据按照一定的线性组合预测当前时刻的样本值[10]。

假设时间序列X={xt},t∈(1,N)，则对于样本值X的预测结果,如式1。

(1)

在公式1中，αi表示预测系数，δ服从NID(0,σ2)的高斯分布。从公式1中可以看出，AR(n)模型的关键是预测系数和δ的误差分布[11]。AR(n)模型有别于经典的LR模型，LR模型是基于预测值本身的特质信息进行预测，而时间序列预测的关键是根据历史时间的观察值预测当前的状态或者观察值。

对公式1进行等式变化，得到式(2)。

(2)

根据式(2)，进行方差运算,得到式(3)。

(3)

根据式(3)可知，AR(n)模型的求解α1,α2,…,αt-n过程实际是求解各个预测系数的问题，可以采用经典的参数估计算法——Levinson—Durbin算法实现参数预测[12]。该算法的主要思路是通过最优化当前的样本序列的预测系数，在满足当前最小化预测误差的前提下使用Yule—Walker方法迭代地求解模型参数。

根据式(1)，为方便公式变化和参数整齐，将式(1)中X用xt代替，公式共同递增xt-k并同时求解期望，如式(4),

(4)

令自相关函数R(k)如式(5),

(5)

根据式(4)和式(5)可以得到预测系数的线性表示方式,如式6。

(6)

2 流量分配预测

网络流量呈现突发式的变化，在固定的网络环境下网络的承载能力是有限的，根据网络历史的负载情况预测当前的网络流量具有非常重要的意义。网络流量在时间上符合一定的时序特性，通过时间序列挖掘分析预测当前时间下的流量。

2.1 粒子群算法

粒子群算法作为一种全局优化算法，通过模拟群鸟觅食的场景而产生，每个粒子都维持一个局部的最优解，时刻调整全局的最优解来更新路径[13]。粒子群算法可描述为在D维空间n个粒子构成的集合X=(X1,X2,…,Xn),每个粒子都维持一个当前的优化速度vi,同时记录当前迭代次数的最优状态和全局的最优状态，动态更新全局最优状态和每个粒子的优化方向,如式(7),

(7)

在式(7)中，pc表示当前最优解，pg表示全局最优解，r表示随机数，η1和η2表示系数[14]。粒子群算法可以归纳为如下步骤。

1) 初始化粒子群，设定初始状态下局部最优解pc和全局最优解pg；

2) 对每个粒子分别比较当前搜索状态下的最优解是否需要更新当前局部最优解；

3) 针对每个粒子的局部最优解和全局最优解进行比较权衡更新；

4) 更新每个粒子的速度和位置信息；

5) 若算法不收敛，则跳转到步骤2继续。

2.2 流量预测

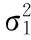
(8)

采用AR(n)模型进行阶数训练时采用AIC准则判断收敛条件，如式9。

(9)

AIC准则[15]需要考虑当前对原始数据的拟合程度又需要考虑模型中参数的个数，设最大阶数为M,M的取值一般为总数据的三分之一。将数据集X中每个分量X(i)表示为X(i)=(x(i-1),x(i-2),…,x(i-p))(i=p+1,…,k),得到式(9)。

(9)

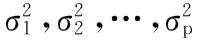
3 实验与分析

试验以本校校园网络作为测试载体，共监听一天的网络流量数据，将一天以小时作为切分单位，共分为24个时间段，选取15个时间段中正常时间段(夜间等时间段需要剔除)，试验以4 ms为一个测试时间段，在15个时间段中随机抽取某个4 ms时间范围进行流量监测。试验首先对比在不同网络负载下本文算法的预测方差如图1所示。

在图1中共对比网络负载在0.2、0、5和0、8 3种情况下本文算法的预测方差，网络负载的值越大表明当前的网络越繁忙，需要处理更多的数据传输。从3种负载情况下的数据对比可以很明显地看出本文算法的预测效果，本文算法在不同网络负载情况下的表现较为明显，网络负载越大方差越小，说明本文算法在网络负载较大时的预测准确性较高。另外，在不同网络负载的情况下方差并非完全单调呈现一定的变化趋势，这与选取的网络时段有关系，4 ms的时间段范围非常窄网络突变情况下网络流量的监测较为不易，对异常网络流量的监测存在一定的不及时性,如图2所示。

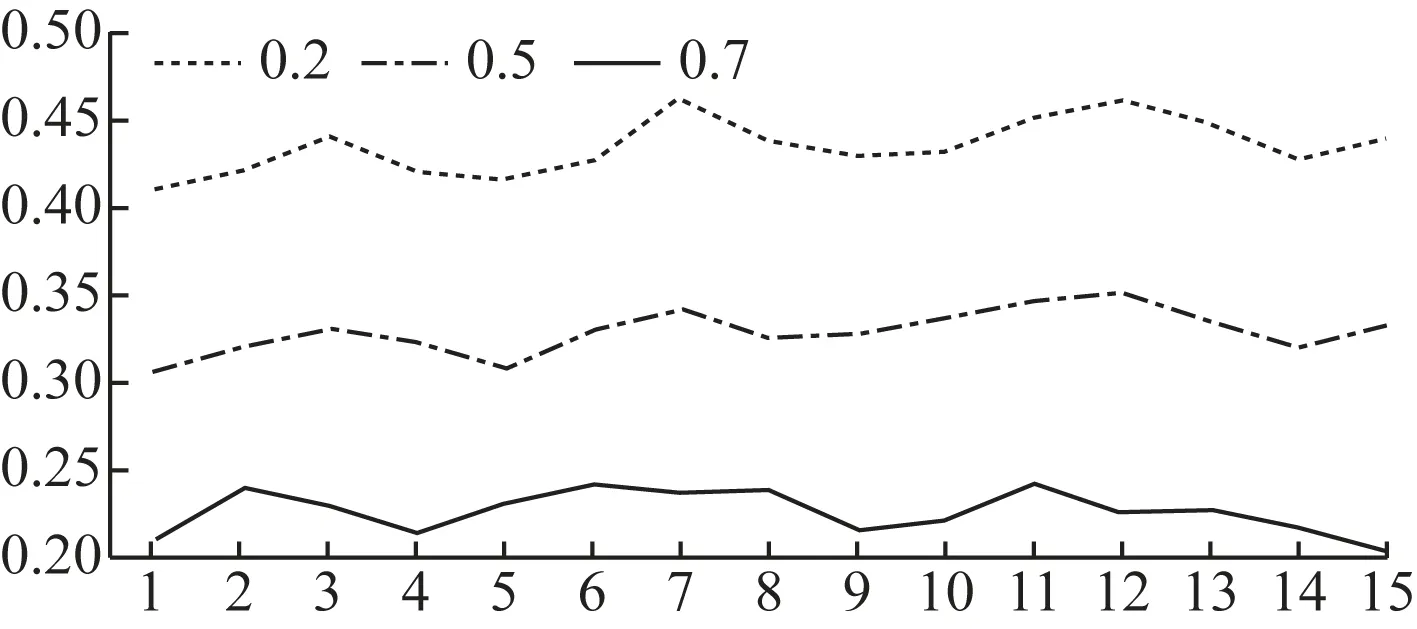
图1 不同网络负载下AR(n)模型预测方差对比图

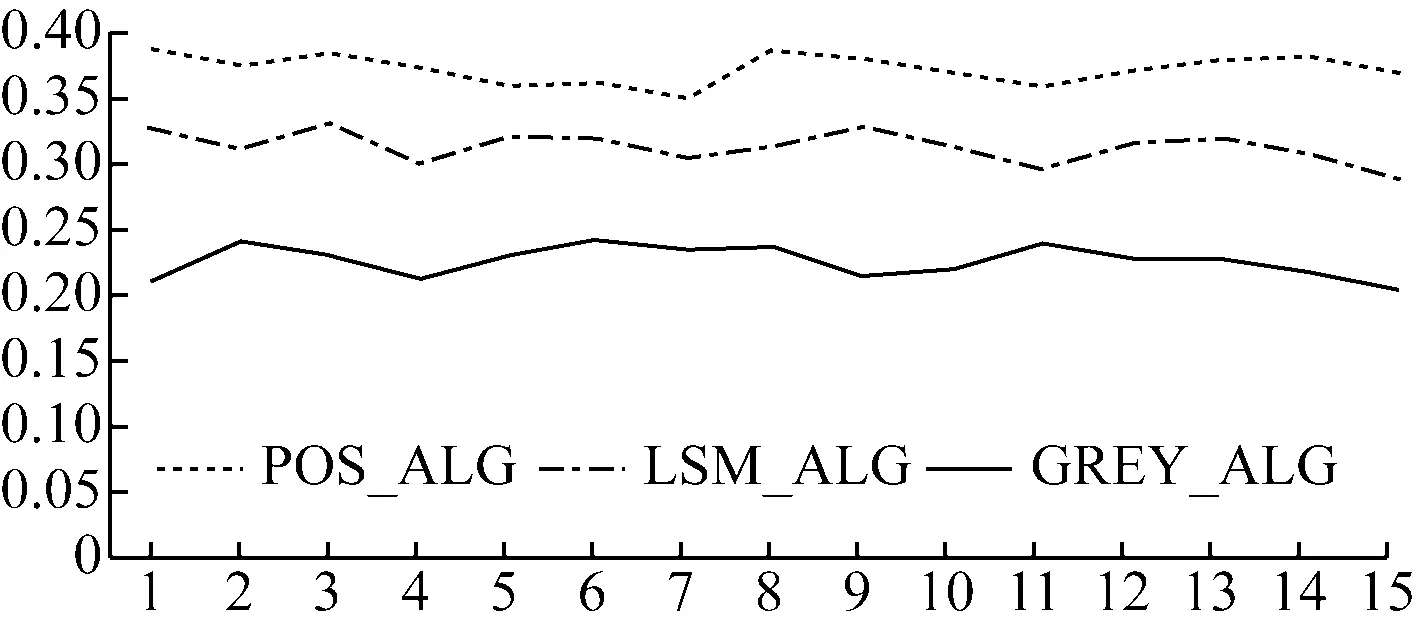
图2 不同算法在网络负载0.8下AR(n)模型预测方差对比图

图2中分别对比了本文算法(POS_ALG)、最小二乘算法(LSM_ALG)、灰色估计算法(GREY_ALG)三种算法在网络负载为0.8时算法的预测情况。从图2中可以看出，本文算法的预测准确性上要优于最小二乘算法和灰色估计算法，另外本文算法的预测准确性也是要优于其它两种算法。相比于在网络负载为0.2和0.5时情况，本文算法的预测效果和最小二乘、灰色估计这两种算法相近。

4 总结

本文分析了当前互联网快速发展时代网络流量突然的情形，网络环境已经从传统的稳定语音传输到流量时刻突变的网络时代，在硬件条件固定的情况下，网络的传输能力是一定的，根据时间序列的预测方式预测网络流量并实时地调整信道传输，从而使得网络数据传输效率最大化。本文以AR(n)模型作为流量预测模型，以粒子群算法训练时序模型的阶数克服了AR(n)模型预测精度不高的缺陷，实验结果表明，本文算法在网络负载较大情况下表现要优于低负载情况，同时对比了最小二乘和灰色估计算法的预测准确性，本文算法预测方差较为稳定且较低，从而表明本文算法具有较高的预测准确性。

[1] 杨斌博,李广成. RoF和xPON的混合组网探讨[J]. 光通信技术,2016,05:1-4.

[2] 邝斌,刘人榕,吴雅婷,等. 基于流量预测的OFDMA-PON动态带宽分配算法[J]. 光通信技术,2016(5):11-14.

[3] 韩丹,陈雪. 结合状态指示和流量预测的GPON DBA算法[J]. 光通信技术,2009(5):14-17.

[4] Chen P, Pedersen T, Bak-Jensen B, et al. ARIMA-based time series model of stochastic wind power generation[J]. IEEE Transactions on Power Systems, 2010, 25(2): 667-676.

[5] 于立晓,陈科明,马琪. 周期可变和流量预测的XG-PON DBA算法[J]. 光通信技术,2011(7):57-59.

[6] 唐丽珠. 出院病人人均医药费用的AR(n)岭估计模型及预测应用[J]. 时代金融,2013(32):302.

[7] 罗娟,唐利民. 正则化的时间序列AR模型及其在经济分析中的应用[J]. 价值工程,2010(2):86-87.

[8] 付子义,吕锁柱,宋昀. 基于多业务预测的EPON动态带宽分配算法[J]. 光通信技术,2010(4):12-14.

[9] 邹锋,汪敏,邹君妮. WDM EPON中的动态波长带宽分配算法[J]. 光通信技术,2008(12):25-28.

[10] Box G E P, Jenkins G M, Reinsel G C, et al. Time series analysis: forecasting and control[M]. John Wiley & Sons, 2015.

[11] 唐毅,刘卫宁,孙棣华,等. 改进时间序列模型在高速公路短时交通流量预测中的应用[J]. 计算机应用研究,2015(1):146-149.

[12] 郭海华,刘瑞瑞. 基于聚类分析和时间序列方法的我国物流量预测研究[J]. 商业经济研究,2015(20):29-30.

[13] Brockwell P J, Davis R A. Time series: Theory and methods[M]. Springer Science & Business Media, 2013.

[14] 邓荣. 基于包络特征的网络流量预测阈值调控算法[J]. 科技通报,2015(10):67-69.

[15] 刘朝霞. 基于随机阵列向量模型的流量预测算法研究[J]. 科技通报,2015(10):196-198.

[16] 张凤荔,赵永亮,王丹,等. 基于流量特征的网络流量预测研究[J]. 计算机科学,2014,04:86-89.

[17] 田梅. 基于混沌时间序列模型的图书借阅流量预测研究[J]. 图书馆理论与实践,2013(7):1-3+26.

Research on Network Bandwidth Allocation Algorithm Based on AR(n) Model

Zhao Ming

(Tianjin Transportation Vocational College，Tianjin 300110, China)

Network burst traffic changes have gradually substituted the smooth voice service, and the network needs to be able to dynamically predict and adjust the flow distribution. AR(n) model, a network traffic prediction algorithm, has several shortages compared with self-similar model on prediction accuracy, but holds well computing performance. Particle swarm optimization algorithm is adopted to optimize the AR(n) model with the AIC criterion. The experimental results on an open dataset show that the improved algorithm acquires well prediction accuracy compared with least-square, grey theory and self-similar models.

AR(n) model; Flow prediction; AIC criterion; PSO algorithm; Prediction accuracy

赵明(1981-)，男，天津人，硕士，讲师，研究方向：软件工程、计算机与网络技术。

1007-757X(2017)06-0061-03

TN929

A

2017.03.29)