基于近似熵快速算法的静息态脑磁信号分析

黄晓霞， 王盼盼

(上海海事大学 信息工程学院， 上海 200135)

基于近似熵快速算法的静息态脑磁信号分析

黄晓霞*， 王盼盼

(上海海事大学 信息工程学院， 上海 200135)

为了探究静息态精神分裂症患者脑磁信号的非线性动力学特性，提出了一种将小波变换和近似熵相结合的特征提取方法.该方法首先通过小波变换，将10个正常人和10个精神分裂症患者的脑磁信号进行6层小波分解，提取对应于脑磁信号θ波段和α波段的小波系数，继而计算和比较两类人近似熵的分布情况.实验结果表明，相同情况下精神分裂症患者MEG信号的各脑区和各通道间的近似熵都普遍高于正常人，α波段的额叶和中央区域尤为突出.该结果为进一步研究患者MEG信号特征进而建立相应的分类诊断模型提供了思路.

脑磁信号； 小波变换； 近似熵； 精神分裂症

精神分裂症是一种多基因遗传病，其临床症状十分复杂，个体心理素质和外部社会环境都会引发该类疾病.发病规律和病理原因至今也尚未明晰，寻找理想的脑疾病诊断工具对精神分裂症进行研究成为当今社会关注的焦点.脑磁图(magnetoencephalography，MEG)能够实现对大脑皮层的精确定位，同时能以ms级的时间分辨率和毫秒级的空间分辨率，无损伤无副作用的探测脑磁生理信号[1].可以将脑磁图作为理想的诊断工具之一，它同功能性磁共振成像(functionalmagneticresonanceimaging，fMR)、脑电图(electroencephalography，EEG)相比有其特有优越性，在临床医学上被广泛应用于精神分裂症、癫痫灶定位和脑肿瘤治疗等领域[2].

脑磁图的现代分析方法大致可以分为时频分析、非线性动力学分析和人工神经网络等[3-4].刻画非线性动力学特性的常见参数有关联维数(correlationdimension，CD)、Lorenz散点图、李雅普诺夫指数(lyapunovexponent，LE)、Lempel-Ziv复杂度和熵等.MahsaTaghavi等[5]通过近似熵(approximateentropy，ApEn)定量分析精神分裂症患者和正常人的EEG信号，发现精神分裂症患者产生更高的ApEn.Kim等[6]应用李雅普诺夫指数，针对25名精神分裂症患者和10名正常人进行研究，发现两类人的李雅普诺夫指数在额叶及颞叶有明显的差异.Takahashi等人[7]应用多尺度熵(multi-scaleentropy，MSE)比较了精神分裂症患者和正常对照组，也发现精神分裂症患者在额叶和中央区域都表现出较高的复杂性.

上述所述的关联维数、李雅普诺夫指数和多尺度熵等非线性动力学参数在表征信号时需要较多的数据点，造成实际应用困难.近似熵很好的解决了该类问题，近似熵只需较短的数据点就可以估计随机信号和确定性信号特性，具有很好的抗噪和抗干扰能力.MEG信号是一种随机性很强的非平稳信号，很适合利用近似熵进行分析，目前采用近似熵对精神分裂症MEG信号进行研究的报道尚未见有.小波变换是信号处理中一种典型的时频分析方法，具有多分辨率特性[8].它既克服了窗口不随频率变化的缺点又继承了短时傅立叶变换的局部化思想，是处理非平稳信号的理想工具.因此，本文重点讨论将小波变换和近似熵结合，来研究精神分裂症患者和正常人MEG信号在α波段和θ波段的近似熵规律，从而发现相应特征.

1实验研究方法

1.1近似熵快速算法

近似熵这一概念是Pincus在20C90S初为了解决混沌现象中求解熵问题而提出的[9]，但该算法在计算过程中存在冗余步骤，计算成本大，计算效率低.因此，Pincus根据实践又给出了一种近似熵实用快速算法，使其计算速度较原算法提升了好几倍.具体算法如下[10-11].

步骤1：定义一个采样点个数为N的MEG信号时间序列为x(1)，x(2)…，x(n).

步骤2：给定阈值r，将N点时间序列组成N*N的二值距离矩阵D，D中的元素用dij表示，定义为第i行元素和第j列元素之间的距离.

(i=1，…，N;j=1，…，N;i≠j).

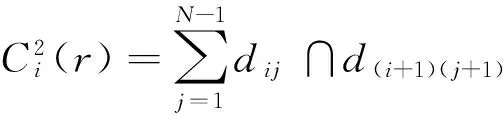
(1)

(2)

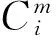
步骤5：当N为有限值时，此时间序列的近似熵为：

ApEn=(N，m，r)=lim[φm(r)-φm+1(r)].

(3)

近似熵是通过一个非负数来度量维数变化时产生新模式的概率大小，近似熵越大，时间序列越复杂，产生新模式的概率也就越大.反之，产生新模式的概率也就越小.上述的近似熵快速算法通过构造距离矩阵来代替原算法中矢量的构造，同时用时间序列中数据点间的差值代替原算法中重复计算相同维数矢量之间的距离，避免了很多不必要的计算步骤.

1.2参数的选取

近似熵的变化与参数的选取有很大的联系，由公式(3)可知，在计算近似熵时需要考虑3个参数的选取，即时间序列长度N，模式维数m，相似容限r，这几个参数一旦确定后，在整个计算过程中都是固定不变的.

对于时间序列长度N，一般取值在100～5 000就能很好的估计出比较稳定的统计值和较小的ApEn伪差[12]，因此在实际应用中N的取值都要控制在此范围内.对于模式维数m的选取，文献[12-13]认为当其通过联合概率对信号进行动态重构时，m=2比m=1能够获得更加详细的信息.对于m>2的情况，则会使通过近似熵分析出来的时间序列丢失许多有用信息，因此在本实验中取m=2.

作为一个有效过滤，r的取值对于整个实验的结果至关重要，Pincus等人在对随机过程和确定性过程的理论分析基础上，总结出r在0.1～0.25 SD(SD为x(i)数据的标准差)之间能够估计出比较有效的统计特性[10]，若r值太小，就不能得到理想的概率统计估计，若r值太大，则会使信号丢失很多有用信息[14].本文通过实验对多个r值进行比较分析，如图1所示，随着相似容限r值的增大，两类人近似熵值逐渐减小，但两者的区分度却逐渐增大，当r=0.2时精神分裂症患者和正常人之间的区分度更加明显.当r值大于0.2时，两类人的区分度又逐渐减小，所以本次实验取r=0.2.

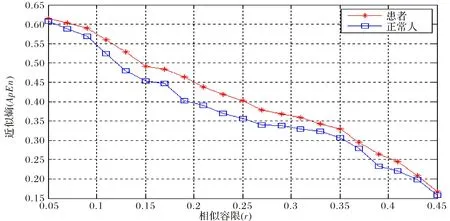
图1 不同相似容限下精神分裂症患者和正常人之间的差异Fig.1 Differences between schizophrenia patients and controls under similar tolerance

2预处理过程

2.1数据来源

实验数据来源于美国国立精神卫生研究所MEG核心实验室(National Institute of Mental Health MEG core Facility).该数据由加拿大VSM MedTech 公司研发的CTF-275超导量子干涉仪(SQUID)设备采集得到，包括精神分裂症患者及正常人两类人的静息态脑磁数据.数据采样频率为600 Hz，采样时间4 min.本次实验选取了10名精神分裂症作为患者组，10名健康正常人作为对照组，采用的脑磁信号数据包含有273个有效通道(F43和O13通道损伤，不能正常工作)，考虑近似熵算法在时间序列长度为100～5 000时分析效果更佳，本次实剔除了受试者可能未完全进入静息态的前1 min数据和出现精神分散的后1 min数据，保留中间部分重采样，重采样频率为150 Hz，采样时间30s，滤波带通为0.5～256 Hz.

2.2ICA去除伪迹

独立成分分析(independent component analysis，ICA)是一种盲源分离技术[15]，在语音分离、特征提取、噪声消除等方面有着广泛应用.脑磁信号的采集过程中，不可避免的会遭受其他干扰源的污染引入其他电生理信号成分，如心电(electrocardiogram，ECG)、眼电(electro-oculogram，EOG)、肌电(electromyogram，EMG)等.因此为了获得相对纯净的脑磁信号，使用ICA将相互独立的干扰源信号从观察信号中分离出来.

图2 伪迹处理后的独立分量时域波形图Fig.2 Independent component time-domain waveforms after artifact processing

图3 原始信号与去噪后信号的对比图Fig.3 The comparison diagram of MEG signals before and after artifacts denoising

图2是经过ICA处理后挑选出来的伪迹独立成分，根据有关伪迹去除的先验知识可知：图2中分量1和分量4的频率较高，幅值较大是肌电伪迹；分量2是眨眼伪迹，分量7是眼动伪迹，分量8的波形呈现一定的规律性是心电伪迹，分量9的波形比较平滑未出现异常波动是正常的脑磁信号.为了不影响实验结果，需要将分量1、2、4、7、8过滤掉.图3是第29个通道伪迹去除前后的对比图，蓝色为原始信号，红色为伪迹去除后的信号.从图中可以看出伪迹去除后的波形更加符合脑磁信号的波形特征.

2.3小波变换提取节律波

利用紧支集正交小波(Daubechies小波)的db3(3是小波阶数)小波函数对经过ICA处理后的脑磁信号进行6层小波分解，即x(n)=A6+D6+D5+D4+D3+D2+D1.理论上[16-17]，在静息态脑磁信号中α波和θ波所占比重较大，因此本文主要研究这两个波段.表1给出了小波变换后，各层频带所对应的节律波以及各节律波的范围.α波对应的频带范围为8～13Hz， D5小波系数重构后的频带范围为8～16Hz，在α波的频带附近，因此提取D5频带对应的能量均值作为特征量.同理，θ波对应的频带范围为4～8Hz，因此提取D6频带对应的能量均值作为特征量.

表1 小波分解各层频带范围

3实验结果与分析

3.1通道间差异

图4分别比较了患者组和正常对照组θ波段和α波段273个通道近似熵均值的分布情况.观察上图可知，在θ波段患者组各通道近似熵均值分布在[0.2993，0.3702]，而正常对照组各通道近似熵均值分布在[0.2652，0.3190].在α波段患者组各通道近似熵均值分布在[0.4545，0.5392]，而正常对照组各通道近似熵均值分布在[0.4416，0.4657].从散点图可看出，不管是在θ波段还是α波段患者组273个通道的近似熵均值均高于正常对照组.θ波段两类人近似熵值在其平均线上下波动幅度较大，且波动幅度和变化趋势较为相似，α波段正常组近似熵值集中分布在平均线附近，上下波动幅度小，而患者组近似熵值分布明显较正常组更加分散，上下波动幅度大，可见在α波段患者组与正常对照组之间的差异性比θ波段更加明显，个体差异性更大.

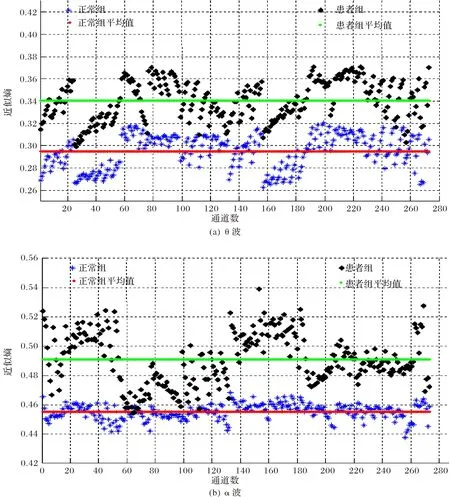
图4 患者组与正常对照组各通道近似熵分布Fig.4 ApEn distribution of each channel between patients and controls

3.2脑区间差异

实验将全头的273个有效通道划分为13个脑区组，其中M表示脑磁信号，L表示左，R表示右，Z表示中线，F为额叶，C为中央区，P为顶叶，O为枕叶，T为颞叶，共组合成13个脑区，即LF、ZF、RF、LC、ZC、RC、LP、RP、LO、ZO、RO、LT和RT.如图5所示，图中蓝色表示正常人，红色表示精神分裂症患者，横轴为13个脑区，纵轴为每个脑区对应的近似熵均值.从图中显示的结果来看，患者组θ波段各脑区近似熵主要分布在[0.3195， 0.3643]，而正常组主要分布在[0.2665， 0.3107].患者组α波段各脑区近似熵主要分布在[0.4604， 0.5185]，而正常组主要分布在[0.4524， 0.4628]分布相对均匀，两者有明显的差异性.由图6可知θ波段的MLC、MLP、MRF、MZF和MZO脑区以及α波段的MLC、 MLF、MRC、MRF、MZC和MZF脑区差异更加明显.其中，

图5 患者组与正常组各脑区ApEn均值分布Fig.5 ApEn mean distribution of each brain area between patients and controls

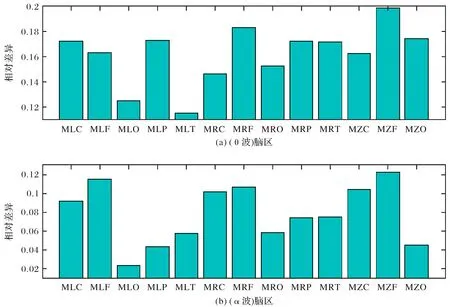
图6 θ波段和α波段通各脑区间的近似熵差异Fig.6 Differences of each brain area between θ rhythm and α rhythm

3.3近似熵的统计图分析

图7是根据两类人θ波段和α波段273个通道近似熵的平均值绘制而成的全头拓扑图.在图中熵值的变化通过颜色来反映，当颜色由蓝到红逐渐变深，表明近似熵的值由小逐渐变大.观察图7可知，在θ波段和α波段患者组的红色区域分布均比正常组分布更加广泛，在α波的额叶和中央区域以及θ波的顶叶和枕叶区域差别更加明显.因为大脑额叶与思考、记忆和个体情感需求密切相关，顶叶对于人的思维逻辑判断起到了重要的作用，而中央区域和枕叶也是大脑结构的重要组成成份，当这些部分受到影响时，大脑活动的逻辑性和连贯性就会受到限制.患者组和正常对照组相比在这些区域的近似熵普遍偏高，说明精神分裂症患者脑磁信号时间序列较无规则.

图7 患者组与正常组近似熵均值拓扑图(左为θ波，右为α波)Fig.7 Topology of ApEn mean between patients and controls (left is θ rhythm and right is α rhythm)

图8 患者组与正常组近似熵的箱型图Fig.8 Boxplot of ApEn between patients and controls

将θ波段和α波段两类人所有通道上的近似熵值平均后，绘制如图8所示的箱型图，该图显示了两组数据的分散情况.从图中可以看出，两种节律波中正常组的方盒长度明显比患者组要短，说明正常组近似熵的正常值分布比较集中，而患者组比较分散.而且，患者组所有通道的近似熵均值也都高于正常对照组，这也从另一方面说明了精神分裂症患者脑磁信号的混乱程度要高于正常人.

4结论

本文将非线性动力学方法和时频分析方法相结合，比较了相同状态下精神分裂症患者和正常人的脑磁信号θ波段和α波段的近似熵特征，实验初步表明在两种节律波中精神分裂症患者的MEG信号近似熵值都显著高于正常人，在α节律波的额叶和中央区域差别更加明显，这对于诊断精神分裂症患者具有一定的参考价值.由于精神分裂症患者的临床表现错综复杂，个体差异，生理状况都有可能影响实验结果.所以今后将从增加实验样本容量，细分信号不同波段等方面入手，使得实验结果更具有普遍性.

致谢 感谢美国国立精神卫生研究所 MEG 科研平台提供的 MEG 研究数据，感谢Tzyy-Ping Jung 教授，Arnold J.Mandell 教授以及加州大学圣迭戈分校计算机系的 Chung-Kuan Cheng教授等对该课题研究的支持与帮助.

[1] 孙吉林. 脑磁图(MEG)常见问题[J]. 现代电生理学杂志， 2005， 12(4):245-249．

[2] DAI Y， ZHANG W， DICKENS D L， et al. Source connectivity analysis from MEG and its application to epilepsy source localization[J]. Brain Topography， 2012， 25(2):157-66．

[3] AFTANAS L I， LOTOVA N V， KOSHDAROV V I， et al. Nonlinear forecasting measurements of the human EEG during evoked emotions[J]. Brain Topography， 1997， 10(2):155-62．

[4] TAKEUCHI F， KAMADA K， KURIKI S. Time-frequency analysis of MEG signals during a visual language task[J]. Transactions of the Japanese Society for Medical & Biological Engineering Bme， 2006， 44:696-701．

[5] TAGHAVI M， BOOSTANI R， SABETI M， et al. Usefulness of approximate entropy in the diagnosis of schizophrenia[J]. Iranian Journal of Psychiatry & Behavioral Sciences， 2011， 5(5):62-70．

[6] KIM D J， JEONG J， CHAE J H， et al. An estimation of the first positive Lyapunov exponent of the EEG in patients with schizophrenia[J]. Psychiatry Research， 2000， 98(3):177-189．

[7] TAKAHASHI T， CHO R Y， MIZUNO T， et al. Antipsychotics reverse abnormal EEG complexity in drug-naive schizophrenia: a multiscale entropy analysis [J]. Neuroimage， 2010， 51(1):173-82．

[8] 张 毅， 罗明伟， 罗 元. 脑电信号的小波变换和样本熵特征提取方法[J]. 智能系统学报， 2012， 7(4):339-344．

[9] PINCUS S M， MULLIGAN T， IRANMANESH A， et al. Older males secrete luteinizing hormone and testosterone more irregularly， and jointly more asynchronously， than younger males[J]. Proceedings of the National Academy of Sciences of the United States of America， 1996， 93(24):14100(1-5)．

[10] PINCUS， S M. Approximate entropy (ApEn) as a complexity measure[J]. Chaos， 1995， 5(1):110-117．

[11] AN X U， LIU J， PENG Q Y， et al. Fast algorithm of dynamic approximate entropy and its application in heart rate variance analysis[J]. Journal of Tongji University， 2005, 33(4):520-524.

[12] CHEN W T, WANG Z Z, REN X M. Characterization of surface EMG signals using improved approximate entropy[J].Journal of Zhejiang University Science(Life Science)2006, 10: 844-848.

[13] YENTES J M， HUNT N， SCHMID K K， et al. The appropriate use of approximate entropy and sample entropy with short data sets[J]. Annals of Biomedical Engineering， 2013， 41(2):349-365.

[14] PINCUS S M. Approximate entropy as a measure of system complexity[J]. Proceedings of the National Academy of Sciences of the United States of America， 1991， 88(6):2297-301．

[15] XIANFENG D U, ZHIJUN L I, FENGRONG B I, et al. Source separation of diesel engine vibration based on the empirical mode decomposition and independent component analysis[J].Chinese Journal of Mechanical Engineering, 2012(3):557-563.

[16] 汤 浩， 卢 青， 韩 莉， 等. 抑郁症住院患者静息态的脑磁频谱分析[J]. 中华精神科杂志， 2012， 45(6):345-348．

[17] HINKLEY L B N， VINOGRADOV S， GUGGISBERG A G， et al. Clinical symptoms and alpha band resting-state functional connectivity imaging in patients with schizophrenia: implications for novel approaches to treatment[J]. Biological Psychiatry， 2011， 70(12):1134-1142．

Resting-state magnetic signals analysis based on the fast algorithm of approximate entropy

HUANG Xiaoxia, WANG Panpan

(Shanghai Maritime University， College of Information Engineering， Shanghai 200135)

In order to study the nonlinear dynamics of the schizophrenic patient’s MEG signals in resting-state, this paper presents a method of feature extraction which combined the wavelet variation with the approximate entropy. The brain magnetic signals of 10 controls and 10 patients are decomposed to six levels by wavelet decomposition and wavelet coefficient is extracted corresponding to the θ rhythm and α rhythm of MEG signals. Then the distribution of approximate entropy between two kinds of people are calculated and compared. The experiment results show that the entropy of each brain region and channel of the MEG signals in schizophrenic patients were generally higher than controls under the same situation, especially frontal and central regions in α rhythm. This result provides a guideline for the study of EEG signal characteristics of the patients and establishes the appropriate classification diagnostic model.

magnetoencephalography; wavelet transform; approximate entropy; schizophrenia

2016-10-21.

第48 批教育部留学回国人员科研启动基金项目．

1000-1190(2017)03-0309-08

R749.3

A

*E-mail: 1946883554@qq.com．