基于差分进化算法的重力固体潮信号独立分量分析
2017-06-27全海燕
高 略, 全海燕
(昆明理工大学 信息工程与自动化学院, 昆明 650500)
基于差分进化算法的重力固体潮信号独立分量分析
高 略, 全海燕*
(昆明理工大学 信息工程与自动化学院, 昆明 650500)
为了提取出重力固体潮信号中的独立谐波成分,基于地球自转与月球、太阳相对于地球轨道变化的正交关系建立一个天体间引潮力的分解模型.为了实现对三者所产生的潮汐谐波的分解,将差分进化算法用于独立分量分析中,用以提高整个算法的效率,改进实验的观测精度,从而更有效的得到与该模型相一致的独立成分.实验中,对昆明地区的实测信号进行了处理并与理论值进行了对比,结果表明,该方法可以将重力固体潮信号中各潮汐谐波分量间关系揭示出来且与分解模型相对应,各分量所含的频谱信息与理论值相一致,说明该方法是一种有效的、对重力固体潮信号进行独立分量分析的新方法.
重力固体潮; 分解模型; 差分进化(DE); 独立分量分析(ICA)
由于日、月相对地球位置的变化,则日、月引力会使地球的重力场随时间产生周期性的变化[1].根据这种变化在重力数值和垂线方向上的不同反映,可将其分为地球重力固体潮和地倾斜固体潮.本文只分析重力固体潮信号.这种重力的潮汐变化对地震的触发有着重要的影响.由于中国是一个地震活动频度高、强度大、分布广的地震灾害严重的国家,又因重力固体潮信号对地震观测,研究地震成因、地震前兆与地震预测有着重要的作用[2].所以重力固体潮信号的分析研究对我国的地震研究的发展具有重要意义.同时,重力固体潮信号中的潮汐谐波分量,其中中包含有丰富的地球物理信息.然而只有提取出重力固体潮信号中的独立谐波分量,才能与相应的天体潮汐谐波对应,才能进一步理解天体间重力的作用规律.然而,一直以来对地球固体潮信号分析的传统方法是对其进行调和分析.目前,主要的分析方法有Venedikov和ETERNA两种调和分析方法.这些方法最后都是基于Fourier变换进行的,然而Fourier分析的信号必须具有线性、高斯性和平稳的特点,仅适用于对信号进行全局分析,不适用于对信进行局部分析[3].这说明调和分析对重力固体潮信号的处理存在一定的局限性,在对重力固体潮信号进行局部分析时不能将其中谐波分量的关系全面揭示出来,提取到的潮汐谐波分量不能与相应天体产生的潮汐谐波逐一对应.
为了有效的提取出重力固体潮信号中包含的地球物理信息,实现该模型所描述的各天体间的对应关系.本文引入了基于DE的ICA算法,并结合正交分解模型对观测信号进行分析和处理,从中得到了解混信号,最后通过Fourier变换对其进行频谱分析,解析出重力固体潮信号中的日波、半日波、长周期波等潮汐谐波分量,揭示出他们与太阳、月球引潮力的对应关系.
通过仿真实验和分析可知,本文提出的改进算法从重力固体潮的潮汐谐波中提取出的独立成分与分解模型逐一对应,且揭示出了重力固体潮信号中潮汐谐波的独立分量与各天体间引力潮汐效应的对应关系.为重力固体潮的研究找到了一个新的方法.
1基于引潮力的分解模型
如图1所示,针对地球上的某观测点A,设其由地球自转、太阳和月亮产生的引潮力为F,F可以分解到指向地心的重力方向与地球水平面方向,其中指向地心方向的引潮力为重力固体潮Fg.此外,Fg又可以可以分解为分量F1和分量F2,由于F1垂直于自转轴方向所以其为自转轴分量,F2平行于地球自转轴方向其为自转面分量[7].F1又可以分解为同2个独立分量Fv和Fh,这样重力固体潮信号就可被分解为一个三维的正交向量,如图1所示.根据三维正交向量分解模型,其中F1既反映地球自转的变化,也反映月球轨道的变化 ,因此主要体现重力固体潮信号的日波、半 日波、月波、半月波等谐波成分.F2和地球自转轴平行,基本不反映地球自转轴的影响,反应地球自转的日波(半日波)系谐波分量很小.
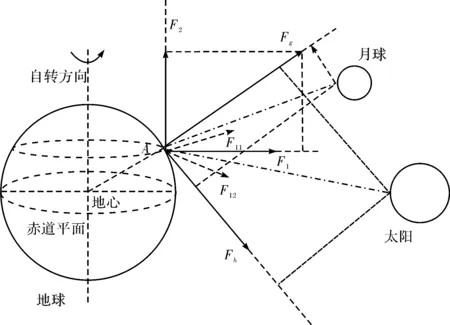
图1 引潮力的分解模型Fig.1 The orthogonal decomposition model of tidal force
2重力固体潮信号的独立潮汐谐波分量提取
2.1ICA算法
ICA是随着盲源分离(Blind Source Separation,BSS)问题于20世纪90年代发展起来的一种新算法.它的实质就是对交叠信号X求解分离(解混)矩阵W2,使Z=W2Y各分量尽量相互独立.独立判据函数为G.具体数学模型如下:
令
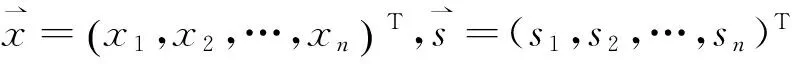
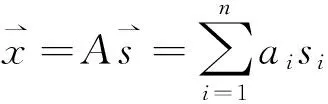
(1)
其中A为混合矩阵,
A-1=W1W2,
(2)
W1为白化矩阵,W2为分离矩阵,
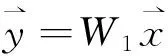
(3)
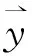
解混模型如下:
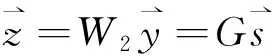
(4)
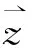
ICA算法包括两个方面:预处理(对X去均值,白化),核心算法(分离矩阵处理),通过以上两个方面得到源信号各个分量的近似估计值.其核心便是建立目标函数和选择优化算法,得到最优的解混矩阵,算法的流程如图2所示.
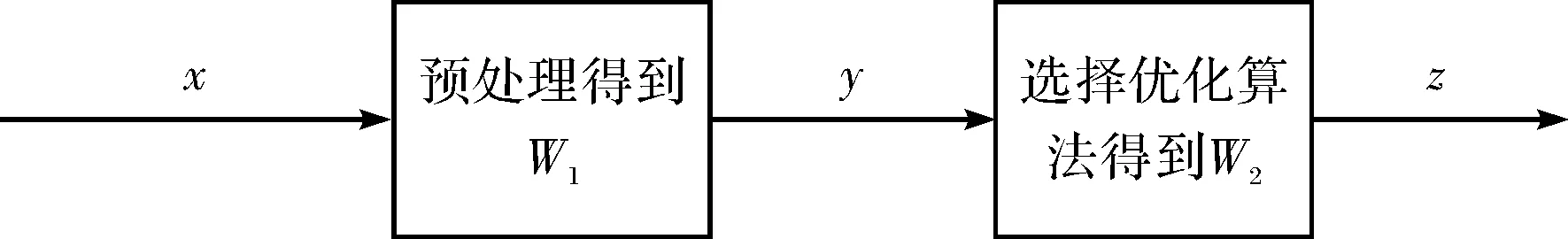
图2 ICA原理图Fig.2 Procedure of ICA
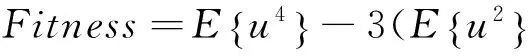
2.2DE算法
根据对ICA算法的初步研究和分析可知,按照目标函数的不同和求解分离矩阵W2的算法不同,可以构成各种ICA算法.但一般的ICA算法的收敛速度较慢,依赖梯度信息、容易陷入局部收索.因此,本文引入了具有全局搜寻及快速收敛特点的差分进化算法.
差分进化算法是一种通过种群内个体间的合作与竞争来对优化问题的求解智能优化算法,其本质是一种基于实数编码的具有保优思想的贪婪遗传算法[8].由于它采取全局的搜索策略,利用实数编码、基于差分的简单变异操作和一对一的竞争生存策略,与传统遗传算法相比,降低了遗传操作的复杂性.
差分进化算法主要是在生成随机初始种群的基础下,经过变异、交叉、选择产生新的种群,寻找最优的粒子.其步骤如下:
1)随机的初始化种群:xi=(xi,1,xi,2,…,xi,D),i=1,2,…,NP.其中D为维数,NP为种群规模.
2)变异
Vi(g+1)=xr1+F(xr2(g)-xr3(g)),
(5)
式中,F为缩放因子.
3)交叉
二项式交叉的公式如下.
ui,j(g+1)=
(6)
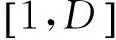
指数交叉
ui,j(g+1)=
(7)
4)选择
xi(g+1)=
(8)
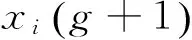
本文所采用的DE算法,除了具有高的可靠性、强鲁棒性、良好的优化性能外,相对其他算法而言需要调控的参数也相对较少.
2.3基于差分进化的重力固体潮信号独立分量分析
在优化过程中,由于DE算法并不依赖被优化问题的信息,而是依据整个种群的动态改变来对收索策略进行调整,达到全局性寻优能力的提高,本文通过利用DE算法优化ICA分析中的分离矩阵来提取重力固体潮信号中的独立成分,其步骤如图3所示.
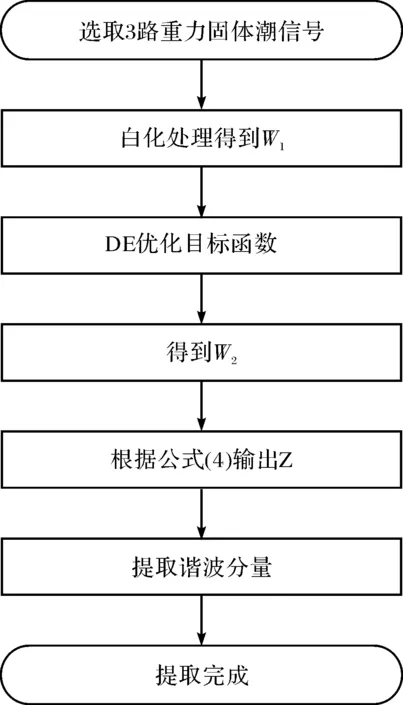
图3 ICA-DE特征提取流程图Fig.3 Flow chart of feature extraction with ICA-DE
步骤1:利用观测点的重力固体潮信号,结合分解模型,分离出的重力固体潮信号独立分量应为3个,而经过ICA后不会降维,故输入重力固体潮信号也定为3路;
步骤2:对重力固体潮信号进行预处理(去均值、白化)得到白化矩阵W1;
步骤3:利用DE算法优化分离矩阵W2;
1) 初始化粒子的种群规模Np及维度nDim,并设置变异率F0,最大迭代次数Gm,交叉率CR,初始化代数G的参数值;
2) 初始化随机种群X;
5) 根据公式(8)进行寻优,若Fitnessnew 步骤5:提取到重力固体潮信号的独立谐波分量,对其进行Fourier变换,分析频谱,然后与理论值相对比. 根据重力固体潮正交分解模型,分离出3个重力固体潮的独立分量,而经过ICA分解后不会降,同时同一经度,不同纬度的重力固体潮信号,在分解到垂直于自转轴平面上的分量没有相位上的差异.所以分别于2010年1月至2010年6月这段时间内,选取了3个位于同一经度不同纬度的观测点(130°E,40°N)、(130°E,50°N)、(130°E,60°N)的重力固体潮信号进行ICA-DE分析.分别得到的了重力固体潮信号波形,如图4所示,独立分量波形如图5所示. 实验中对DE算法参数的设置,如表1所示. 表1 参数设置 图4 重力固体潮信号Fig.4 Gravity earth tide signals 图5 ICA独立分量波形Fig.5 Waveform of independent component of ICA 由如图5可以看出提取出的谐波分量之间存在着明显的调制关系.为了检验所得结果的可靠性,如图6所示分析了解混信号的频谱.根据英国人杜森提出的杜森展开公式得到潮汐谐波的角频率[1].二者进行对比,结果如表2所示,并对得到的独立谐波分量进行分类. 图6 频谱分析Fig.6 Spectrum analysis of independent component 由表2可知: 1) 3路解混输出信号频率的观测值与理论值相一致,且三个独立分量y1(t)、y2(t)、y3(t)分别与相应的地球物理信息相对应; 2) 输出的三路独立分量分别与模型中的信号分量F2、FV、Fh、逐一对应,且互不干扰,证明了重力固体潮信号正交分解模型的有效性. 表2 采样点频率与理论频率对照表 本文基于地球、月球、太阳三个天体间的潮汐谐波相互独立的基础上,建立了一个正交分解模型,将DE智能优化算法引入ICA中对重力固体潮信号进行优化分解,所分解出的独立成分与地球、月球、太阳等天体所产生的引力潮汐相对应,其中重力固体潮信号的日波分量体现在F11方向、 半 日波分量体现在F12方向.年波、半年波等体分量现在F2方向,可以看出F11、F12、F2是相互正交的,这表明ICA-DE算法能够将三维空间下的混合信号分解到三维的独立正交的方向上.简化了信号的解析步骤. 通过对本文所提取的频谱信息分析实现了重力固体潮信号中潮汐谐波独立成分与天体引力潮汐效应的对应关系.同时根据所提取的日波、半日波、长周期波等地球物理信息,可以证明本算法是有效的,跟其他方法对比显得更加简便.此外,通过观察重力固体潮信号中提取出的独立分量中仍存在乘性调制关系.这为下一步的研究提供了一个很好的切入点. [1] 管泽霖, 宁津生. 地球形状及外部重力场[M].北京:测绘出版社,1981. [2] 张 立, 傅容珊, 周 挚, 等. 基于HHT提取重力固体潮的地震前兆信息[J]. 地球学报, 2007, 29(2): 223-226. [3] 周 挚, 山秀明, 张 立, 等. 基于HHT提取昆明、下关重力固体潮的地震前兆信息[J]. 地球物理学报, 2008, 51(3);836-844. [4] 李巧燕, 全海燕. 基于ICA的重力固体潮信号的潮汐谐波提取[J]. 昆明:云南大学学报(自然科学版), 2015, 37(6): 845-850. [5] 吴庆畅, 周 挚, 梁 虹, 等. 重力固体潮IMF的AM-FM模型及其非线性拟合[J].计算机工程与应用, 2009, 45(30): 138-142. [6] 张春美. 差分进化算法理论与运用[M].北京:北京理工大学出版社,2014. [7] 李云飞. 基于改进的HHT方法提取重力固体潮信号的地球物理信息[D]. 昆明: 昆明理工大学,2014. [8] 刘 波, 王 凌, 金以惠. 差分进化算法研究进展[J]. 控制与决策, 2007, 22(7): 722-729. [9] CHENG F S, ZHOU H Y, CHENG L Q. Improved differential evolution algorithms[J]. IEEE International Conference on Computer Science and AutomationEngineering(CSAE).2012(3):142-145. [10] LI G Y, LIU M G. The summary of differential evolution algorithm and its improvements[C]//2010 3rd International Conference on Advanced Computer Theory and Engineering(ICACTE) , 2010(3):153-156. [11] 朱文龙, 周建中, 肖 剑, 等. 独立分量分析—经验模态分解特征提取在水电机组振动信号中的应用[J].中国电机工程学报, 2013, 33(29): 95-101. [12] 崔玲丽, 吴春光, 邬 娜. 基于EMD与ICA的滚动轴承复合故障诊断[J]. 北京工业大学学报, 2014, 40(10):1459-1464. [13] 梁 亮, 杨敏华, 李英芳. 基于ICA与SVM算法的高光谱遥感影像分类[J]. 光谱学与光谱分析, 2010, 30(10): 2725-2728. [14] 孙和平, 徐厚泽, 陈 斌, 等. 香港地区重力固体潮和海潮负荷特征研究[J]. 地球物理学报, 2006, 49(3): 725-734. [15] 余先川, 胡 丹. 盲源分离理论与应用[M]. 北京:科学出版社,2001. ICA and gravity earth tide signals based on DE GAO Lue, QUAN Haiyan (Faculty of Information Engineering and Automation, Kunming University of Science and Technology, Kunming 650500) The purpose of this work is to solve the difficulty of extracting orthogonal component of tidal harmonic from gravity earth tide signals. An orthogonal decomposition model for gravity earth tide signal is proposed in this paper. Orthogonal decomposition is implemented by the above model from the aspect of space on the harmonic component of the gravity earth tide signal in order for the extracted harmonic component frequency to reflect the independent geophysical information on space. Thus, a new feature extraction method of gravity earth tide signal is presented by combining independent component analysis(ICA)and differential evolution (DE)algorithm, which is more effective to generate the independent component which is consistent with the gravity solid tidal signal decomposition model. In the experiment, the measured signal is processed and compared with the theoretical value in Kunming area. Experimental result shows that the method is able to reveal the relationship of tidal harmonic component in gravity earth tide signals, which is corresponding to the gravity earth tide signal orthogonal decomposition model. Each component contains spectral information consistent with with theory value. These results indicate that this method is effective and a novle method of orthogonal analysis for gravity solid signal. gravity earth tide signal; orthogonal decomposition model of gravity earth tide signal; differential evolution; independent component analysis 2016-12-17. 国家自然科学基金项目(41364002). 1000-1190(2017)03-0293-05 P312.4 A *通讯联系人. E-mail: quanhaiyan@163.com.3实验结果与讨论

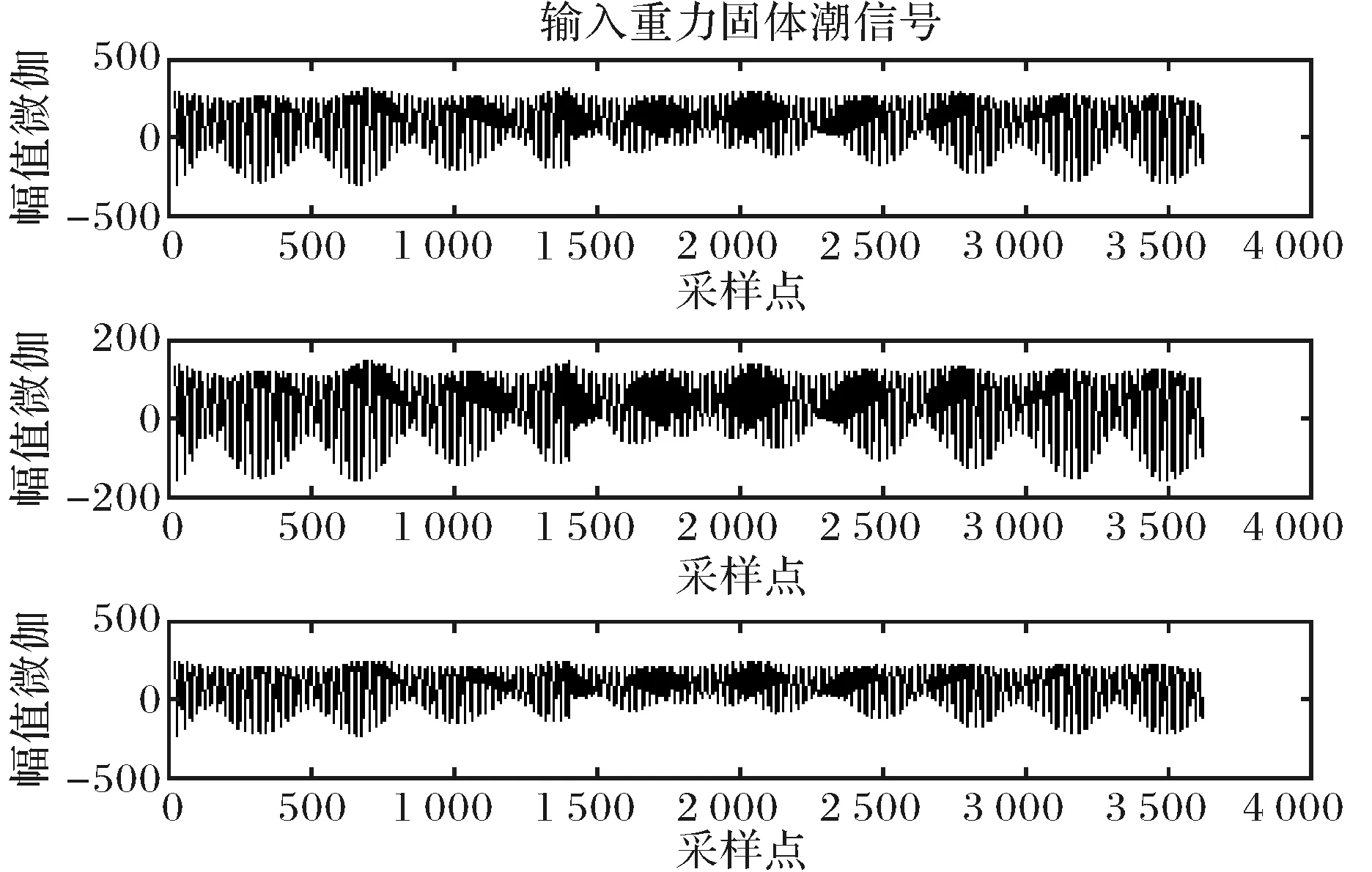
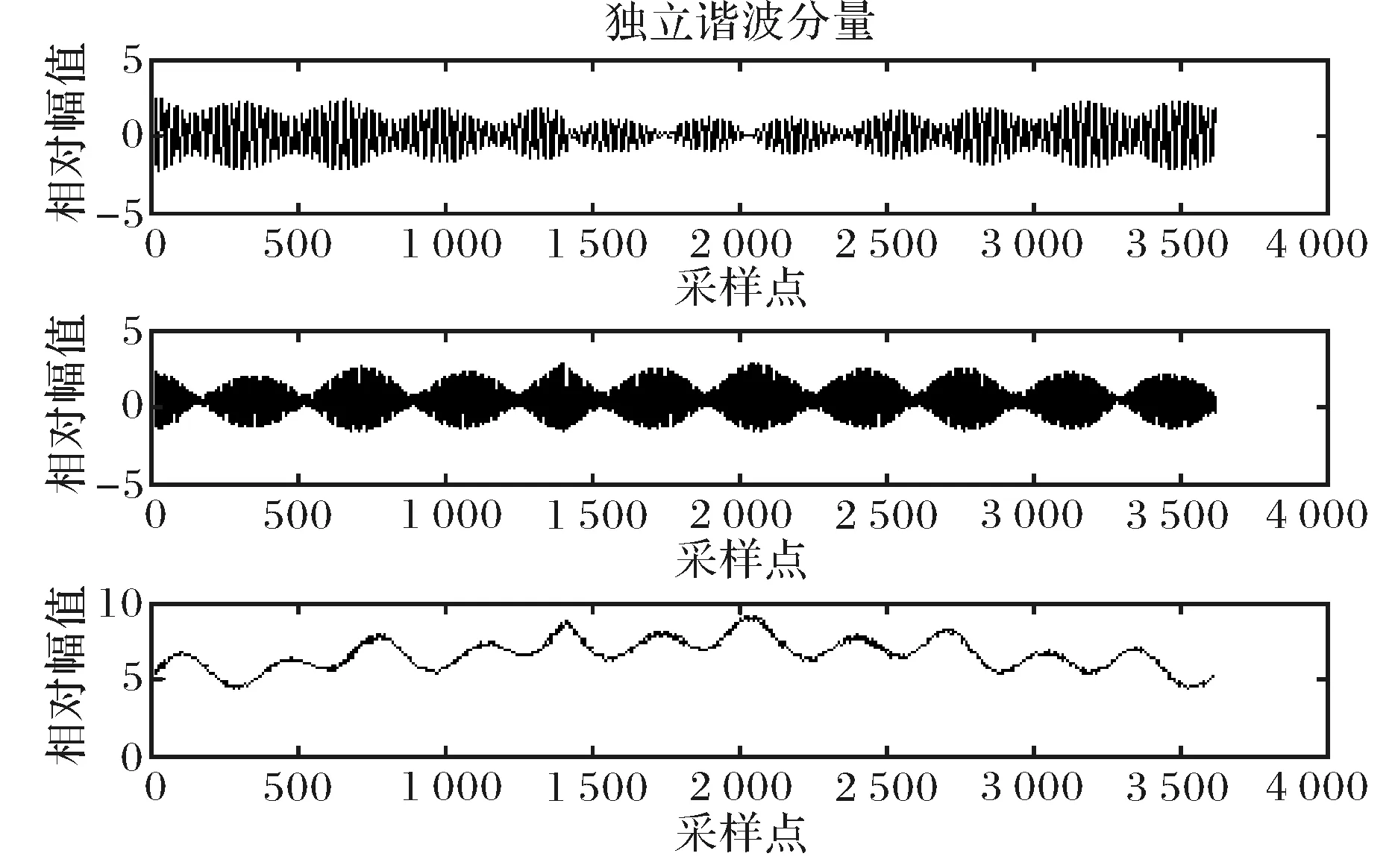
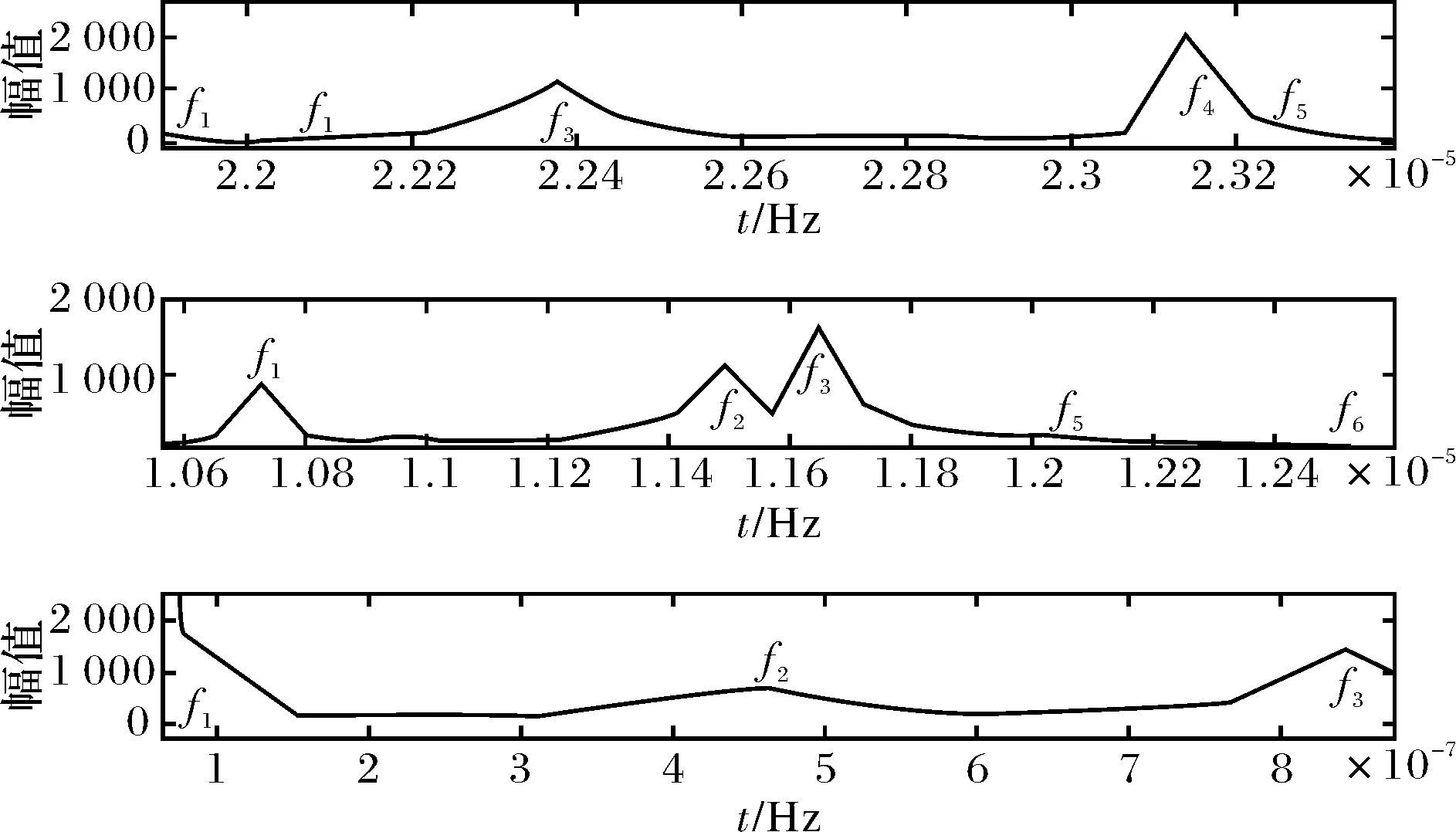

4结论
