具有粗糙初值的Landau-Lifshitz-Gilbert方程的整体解的存在性

林俊宇, 徐晓杰

(华南理工大学理学院数学系, 广州 510640)

具有粗糙初值的Landau-Lifshitz-Gilbert方程的整体解的存在性

林俊宇*, 徐晓杰

(华南理工大学理学院数学系, 广州 510640)

关注高维Landau-Lifshitz-Gilbert方程的整体解的存在性问题,证明了当初始值半范数[Z0(x)]BMO(Rn)充分小时,Landau-Lifshitz-Gilbert方程柯西问题存在整体解:通过球面投射的方法,把Landau-Lifshitz-Gilbert方程转化为一个非线性Schrödinger方程,然后研究该方程的整体解的存在性,最后通过逆运算,得到原Landau-Lifshitz-Gilbert方程的解的整体存在性.

Landau-Lifshitz-Gilbert方程; 存在性; 球面投射

LANDAU与LIFSHITZ[1]在1935年提出了铁磁体运动的方程Zt=1Z(x,t)×Heff(x,t)-2Z(x,t)×(Z(x,t)×Heff(x,t))

((x,t)Rn×(0,+)),

(1)

Z(x,t)=Z0(x)S2((x,t)Rn×{t=0}),

(2)

其中Z(x,t)=(Z1(x,t),Z2(x,t),Z3(x,t)):Rn×(0,+)→S2为磁化强度向量,这里Zi(x,t)(i=1,2,3)为数量函数,S2⊂R3为单位球面,×表示Rn中的向量积,1为常数,常数2>0为Gilbert阻尼系数,Heff为有效场. 当有效场只有交换场时,即Heff=△Z,由方程(1)、(2)得到Landau-Lifshitz-Gilbert方程:

Zt=2ΔZ(x，t)+2|Z(x，t)|2Z(x，t)+1Z(x，t)×

ΔZ(x，t) ((x,t)Rn×(0,+)),

(3)

Z(x,0)=Z0(x)S2((x,t)Rn×{t=0}).

(4)

方程(3)与调和映照热流、Schrödinger流有密切的联系:当1=0时,方程(3)变成了调和映照热流:

Zt=2△Z(x,t)+2|Z(x,t)|2Z(x,t);

Zt=1Z(x,t)×△Z(x,t).

我们知道,方程(3)具有平移和伸缩不变性,即对于任意的(x0,t0)Rn×(0,+)及η>0,若Z(x,t)满足方程(3),则Zη(x,t)∶=Z(x0+ηx,t0+η2t)也满足方程(3).

当n=2时,借鉴调和映照热流的办法,文献[2-5]得到了方程(3)的几乎光滑解的存在性以及能量递减解的唯一性.

当n≥3时,文献[6]得到了方程(3)整体弱解的存在性. 但是方程(3)没有与调和映照热流类似Bochner公式和能量单调不等式,所以，研究方程(3)的弱解的正则性以及唯一性具有一定的难度. 文献[7]、[8]研究了三维、四维驻定弱解的部分正则性,文献[9]、[10]得到了三维、四维Ginzburg-Landau逼近弱解的部分正则性.

对于 Landau-Lishitz-Gilbert 方程的正则性的问题,DING和WANG[11]首次证明了当n=3 和n=4 时一类初边值问题奇性解的存在性,这一结果对 Landau-Lishitz-Gilbert 方程的研究起着重要的作用. 同时,对于 Landau-Lishitz-Gilbert 方程的研究成果还可参考文献[12].

近年来,通过将方程(3)转换为复杂的 Ginzburg-Landau 型的非线性耗散Schrodinger 方程, 得到方程(3)在Ln(Rn)空间和Morrey空间中小初值整体局适定性[13-14];研究了临界Besov空间小初值的整体存在性问题[15]. 但在更大空间中的小初值问题的整体适定性还需要进一步解决.

本文将在更大的空间中研究Landau-Lishitz-Gilbert 方程具有小初值的整体适定性. 为方便起见,设1=1. 在初始值[Z0(x)]BMO(Rn)充分小的条件下,通过球面投射的方法,把Landau-Lifshitz-Gilbert方程转化为一个非线性Schrödinger方程, 然后研究该方程的整体解的存在性. 最后通过逆运算, 得到Landau-Lifshitz-Gilbert方程柯西问题的整体解的存在性. 由Ln(Rn)空间、 Morrey空间与BMO空间的关系,本文所得的结论部分改进了文献[13]和文献[14]的结果.

为了研究方程(3)、(4)的解,引入复函数

(5)

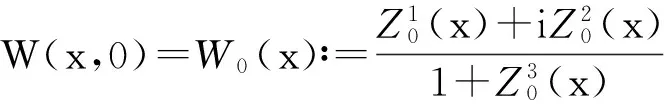
(6)

那么BMO半范数有下面的等价形式[17]:

再定义2个函数空间

X∶= {f:Rn×(0,+)→|‖f‖X≡

Y∶={g:Rn×(0,+)→,

以及

可知,(X,‖·‖X)和(Y,‖·‖Y)都是Banach空间[17].

同时,记

下面给出一些有关的估计.

引理1 如果W0(x)BMO(Rn),则存在常数C>0,使得以下估计成立:

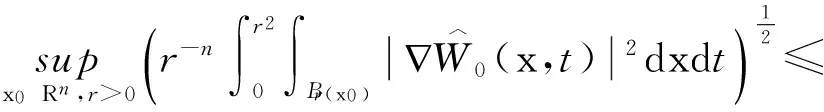
类似文献[17]的式(2.6)的证明可以得到引理 1, 在此略.

引理2 如果gY,那么SgX,并且存在常数C>0,使得‖Sg‖X≤C‖g‖Y.

类似文献[17]的引理3.1的证明可以得到引理1,在此略.

下面在Z0(x)S2以及(x)>-1的条件下, 研究方程(5)、(6)的整体解的存在性. 首先,定义X上的一个映射,其中

引理3 如果[W0(x)]BMO(Rn)<ε,那么存在一个依赖于n的正常数C,使得对于任意的W都有‖W(·,t)‖L(Rn)≤C以及 [W]X≤2ε.

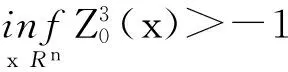
|W(x,t)|≤|W(x,t)-W0(x)|+|W0(x)|≤

另外,由引理 1 可知

ε+[W0]BMO(Rn)≤2ε.

证毕.

证明 由引理 2和引理 3可知,对于任意的W,有‖‖X≤CF(W)Y=

因此, 只要取足够小的ε1>0,则引理 4成立.

引理5 存在ε2(0,ε1],使得如果[W0]BMO(Rn)≤ε2, 那么T是从映到的压缩映射.

证明 对于任意的W1、W2,记W=W1-W2,有

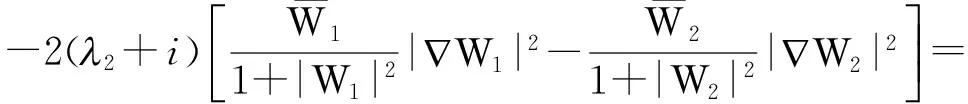
‖F(W1)-F(W2)X‖≤

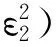
下面给出本文的主要结果.

定理1 设Z0(x)S2且满足,那么存在ε0>0,使得当[Z0(x)]BMO(Rn)<ε0时,方程(3)、(4)存在唯一的整体解Z(x,t),对几乎处处的(x,t)Rn×(0,+),有|Z(x,t)|=1以及

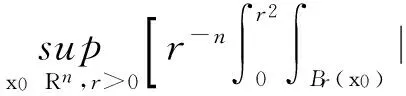
证明 选取ε≤ε2,其中ε2由引理 5得到.

首先,证明在定理1的假设条件下有[W0]BMO(Rn)≤Cε0,其中常数C>0只与n有关.

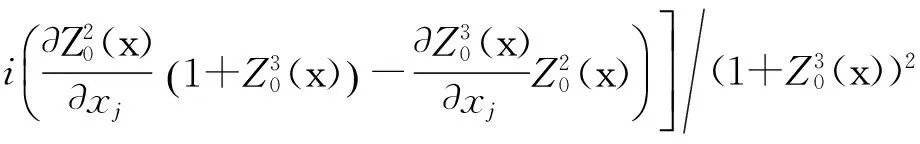
2|Z0(x)|≤|Z0(x)|.由BMO半范数的等价定义可知,如果[Z0(x)]BMO<ε0,那么存在只与n有关的常数C>0,使得

[W0(x)]BMO≤Cε0.

接着,由引理3～引理5以及压缩不动点定理可知,方程(5)、(6)存在唯一解WX.

,

,

.

另外,不难证明

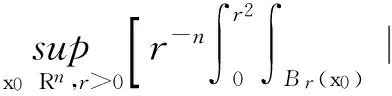
[1] LANDAU L,LIFSHITZ G. On the theory of the dispersion of magnetic permeability in ferromagnetic bodies[J]. Physis Zeitsch der Sow,1935,8:153-169.

[2] CHEN Y,DING S J,GUO B L. Partial regularity for two-dimensional Landau-Lifshitz equations[J]. Acta Mathe-matica Sinica:English Series,1998,14(3):423-432.

[3] GUO B L,HONG M C. The Landau-Lifshitz equation of the ferromagnetic spin chain and harmonic maps[J]. Calculus of Variations and Partial Differential Equations,1993,1:311-334.

[4] HARPES P. Uniqueness and bubbling of the 2-dimensional Landau-Lifshitz flow[J]. Calculus of Variations and Partial Differential Equations,2004,20:213-229.

[5] HARPES P. Bubbling of approximations for the 2-dimensional Landau-Lifshitz flow[J]. Communications in Partial Differential Equations,2006,30:1-20.

[6] ALOUGES F,SOYEUR A. On globla weak solutions for the Landau-Lifshitz equations:existence and nonuniqueness[J]. Nonlinear Analysis,1992,18:1071-1084.

[7] MOSER R. Partial regularity for harmonic maps and related problems[M]. Singapore:World Scientific,2005.

[8] DING S J,GUO B L. Hausdoff measure of the sigular set of Landau-Lifshitz equations with a nonlocal term[J]. Communications in Mathematical Physics,2004,250(1):95-117.

[9] MELCHER C. Existence of partially regular solutions for Landau-Lifshitz equations in3[J].CommunicationsinPartialDifferentialEquations,2005,30:567-587.

[10]WANGC.OnLandau-Lifshitzequationsindimesionatmostfour[J].IndianaUniversityMathematicsJournal,2006,55(6):1615-1644.

[11]DINGSJ,WANGCY.FinittimesingularityoftheLandau-Lifshitz-Gilberequation[J].InternationalMathemati-csResearchNotices,2007,2007(4):1757-1762.

[12]GUOBL,DINGSJ.Landau-Lifshitzequations[M].Singapore:WorldScientificPublishingCompany,2008.

[13]MELCHERC.GlobalsolvabilityoftheCauchyproblemfortheLanda-Lifshitz-Gilbertequationinhigherdimensions[J].IndianaUniversityMathematicsJournal,2012,61:1175-1200.

[14]LINJ,LAIB,WANGC.GlobalWell-PosednessoftheLandau-LifshitzGilbertequationforinitialdatainMorreyspace[J].CalculusofVariationsandPartialDifferentialEquations,2015,54(1):665-692.

[15]GUOZH,HUANGCY.TheinviscidlimitfortheLandau-Lifshitzequation[J].Mathematics,2015,arXiv:1508.07118,20pp.

[16]LAKSHMANANM,NAKAMURAK.Landau-Lifshitzequationofferromagnetism:exacttreatmentoftheGilbertdamping[J].PhysicalReviewLetters,1984,53:665-692.

[17]WANGC.Well-posednessfortheheatflowofharmonicmapsandtheliquidcrystalflowwithroughinitialdata[J].ArchiveforRationalMechanicsandAnalysis,2011,200:1-19.

【中文责编：庄晓琼 英文审校：肖菁】

Global Existence of Landau-Lifshitz-Gilbert System with Rough Initial Data

LIN Junyu*, XU Xiaojie

(Department of Mathematics, South China University of Technology, Guangzhou 510640, China)

The global solutions to Landau-Lifshitz-Gilbert equation in high dimensions are considered. The global well-posedness of the Cauchy problem of the Landau-Lifshitz-Gilbert equation in Rnfor any initial dataZ0(x)S2withsmall[Z0(x)]BMO(Rn)isestablished.ThemethodisbasedonprioriestimatesofanonlinearSchrödingerequationobtainedfromtheLandau-Lifshitz-Gilbertequationbythestereographicprojection.

Landau-Lifshitz-Gilbert equation; existence; stereographic projection

2016-11-21 《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

国家自然科学基金项目(11571117);广东省自然科学基金项目(2016A030313451);中央高校基本科研业务费专项资金项目(2015ZM183)

O175.26; O175.29

A

1000-5463(2017)03-0097-05

*通讯作者:林俊宇,副教授,Email:scjylin@scut.edu.cn.