交叉相关ISAR快速包络对齐方法*

闫雅琼，贺志毅

(1.中国航天科工集团 第二研究院，北京 100854；2.北京遥感设备研究所，北京 100854)

交叉相关ISAR快速包络对齐方法*

闫雅琼1，2，贺志毅2

(1.中国航天科工集团 第二研究院，北京 100854；2.北京遥感设备研究所，北京 100854)

逆合成孔径雷达成像(ISAR)的第1步是运动补偿，而包络对齐是运动补偿的第一步，决定了ISAR系统相位补偿，方位向定标等后续处理的精度，因此对于运动补偿非常关键。现有的包络对齐方法，大都基于相邻包络的相关法，容易产生漂移误差，突跳误差和积累误差，影响包络对齐的精度。分析了这3种误差出现的原因，提出了采用交叉相关的包络对齐方法，该方法在不增加运算量的情况下，消除了这3种误差，仿真实验证明了该方法简单有效适合工程应用。

交叉相关法；包络对齐；漂移误差；突跳误差；积累误差；运动补偿；ISAR成像

0 引言

ISAR可以全天时全天候对非合作远距离运动目标成像，在军事和民用领域应用广泛。ISAR系统将目标的运动分解为转动分量和平动分量，通过运动补偿技术抵消运动目标的平动分量，从而将目标运动转化为ISAR典型的转台运动模型实现方位向分辨。因此运动补偿是ISAR成像的关键步骤，ISAR运动补偿分为包络对齐和相位补偿两步，包络对齐是相位补偿的基础。

自从20世纪80年代Chen[1]开创性提出基于相关的包络对齐方法以来，国内外学者在这一方面做了大量工作[2-15]，如频域法[2，10]，最小熵法[3，9]，子孔径法[4]，超分辨法[4-5]等，这些方法一方面是从参考包络的选取上提高精度，如采用已对齐包络的加权，加窗处理等方法；另一方面是从包络对齐的衡量标准提高精度，如最小熵，最大峰度法等，但是这些方法没有从根本上解决包络对齐过程中容易出现的漂移误差，积累误差和突跳误差，且有些方法采用二维迭代搜索，超分辨等方法寻求相邻包络的距离走动，计算量大，且不稳定，对实时性强的系统并不适用。

基于对现有方法的研究，本文提出采用交叉相关的方法进行包络对齐，本方法采用固定参考一维距离像进行包络对齐，且可以在一定范围内估计目标的径向运动速度，不仅克服了传统基于相邻包络相关对齐方法常有的3种误差，而且运算量小，适合实时性高的SAR/ISAR系统使用，仿真实验证明了本方法的有效性。

1 包络对齐的信号模型及误差分析

包络对齐是为了消除由于雷达和目标的相对运动造成的相邻回波在距离向上的错位，使各个散射点在成像期间处于相同的距离单元内，误差在半个距离单元之内就不影响ISAR运动补偿的下一步精补偿。目前基于相关法的包络对齐是公认效果较好的包络对齐方法，也是目前主流包络对齐方法。

假设相邻两次回波的实包络分别为si-1(n)和si(n)，以si-1(n)为基准，对si(n)作圆周移位后求取其互相关值：

(1)

对r(m)搜索使其获得最大值的移位m，对si(n)进行圆周移位就可以获得包络对齐的效果。

从相邻互相关法包络对齐的思路可以看到，相邻互相关法很容易发生突跳误差，因为虽然ISAR系统重频较高，相邻一维距离像相关性较强，但是实际数据中也会由于散射点之间的干涉作用，雷达的机动等原因，导致距离像会出现某一次或某几次有较大起伏，随即又恢复正常的情况，如果只采用相邻距离像的相关性进行移位，就容易发生突跳误差，进而引起漂移误差和积累误差。

现有研究中对突跳误差的解决方法，大多是采用已对齐包络进行加权作为参考包络，这样由于某一次或者几次距离像的突跳对后续距离像对齐的影响就会减小，因为随着已对齐包络个数的增加，发生突跳的距离像被已经对齐的距离像平均，在参考距离像的计算中不再起关键性作用，因而误差就会减小。但是这种方法窗中窗函数的选择是关键，选择较长的窗函数可以充分利用已对齐的距离像结果，但是待对齐的距离像与之相关性就会减小，进而增大对齐误差，选择较小窗函数不能避免突跳误差的影响，因此该方法没有从根本上解决问题。

漂移误差和积累误差的产生同突跳误差，也是相邻一维距离像对齐误差的积累结果，因此本文针对相邻包络相关法的缺陷提出一种交叉相关的包络对齐方法，该方法从参考距离像的选择，突跳误差的抑制的角度实现包络对齐，且运算量不增加。

2 交叉相关法

交叉相关法是气象学中常用的对气流，风暴，云团运动进行短时预测的方法[13-15]，利用信号之间的相关性特质，根据交叉相关系数预测信号在相关时间内的移动。由于在实时性高的系统中ISAR系统方位向采样率高，目标转角变化很小，短时间内回波的一维距离像相关性强，因此可以将交叉相关法扩展到包络对齐方面的应用，具体过程如下。

首先选定参考一维距离像，依次将其他一维距离像分别与参考距离像相关处理，一维搜索峰值位置即对应于该一维距离像相对于参考一维距离像的平移，将各个一维距离像与参考一维距离像对齐，即达到包络对齐的效果。该方法适用于积累时间内目标做匀速运动的情况，假设回波信号为Es(m，n)，m代表慢时间采样，m=1，2，…，M，n代表快时间采样，n=1，2，…，N，具体步骤如下：

(1) 首先对回波信号距离维做一维FFT，得到各个一维距离像RPm，m=1，2，…，M。

(2) 选择参考距离像，一般选第1个一维距离像，因为第一个一维距离像相对于其他一维距离像的偏移，要么向前，要么向后。

(3) 依次计算参与成像回波与参考距离像的交叉相关因子为

(2)

式中：RPref为参考一维距离像；RPm为待对齐的一维距离像。

(4) 交叉相关因子向量的峰值代表该一维距离像相对于参考距离像的偏移的时间单元为

Km=index[max(CCRm)]，m=1，2，…，M-1.

(3)

(5) 对各个一维距离像相对于参考距离像的偏移做平滑处理，使得相邻一维距离像的偏移值接近于常数为

(4)

(6) 由此可以计算各个距离像RPm相对于参考距离像RPref的距离走动为

(5)

式中：Δr为距离分辨单元，Δr=c/(2B)。

(7) 最后对各个距离像RPm的相位补偿相量为

(6)

最终经过运动补偿的距离像为

(7)

对各个距离像进行相位纠正后，即可消除距离走动等径向运动对成像造成的影响，采用常规的RD方法成像。

经过以上分析可以得到交叉相关法相对于传统包络对齐方法的优点：①抑制积累误差，该方法不利用相邻一维距离像的相关性，也不需要进行加权处理等操作，抑制了积累误差；②抑制漂移误差，即便参考距离像已经有一定的漂移误差，对齐后只影响成像结果目标在方位向的位置，不影响后期的方位向聚焦处理；③抑制突跳误差，该方法对各个距离像相对参考距离像平移量进行平滑，抑制了突跳误差。

3 仿真校验

3.1 仿真条件

取图1中飞机散射点模型，设定目标运动参数如表1，雷达参数如表2。

图1 飞机散射点模型Fig.1 Aircraft scattering point model

参数数值径向速度/(m·s-1)70加速度/(m·s-2)0.1旋转速度/((°)·s-1)1.7初始距离/km16

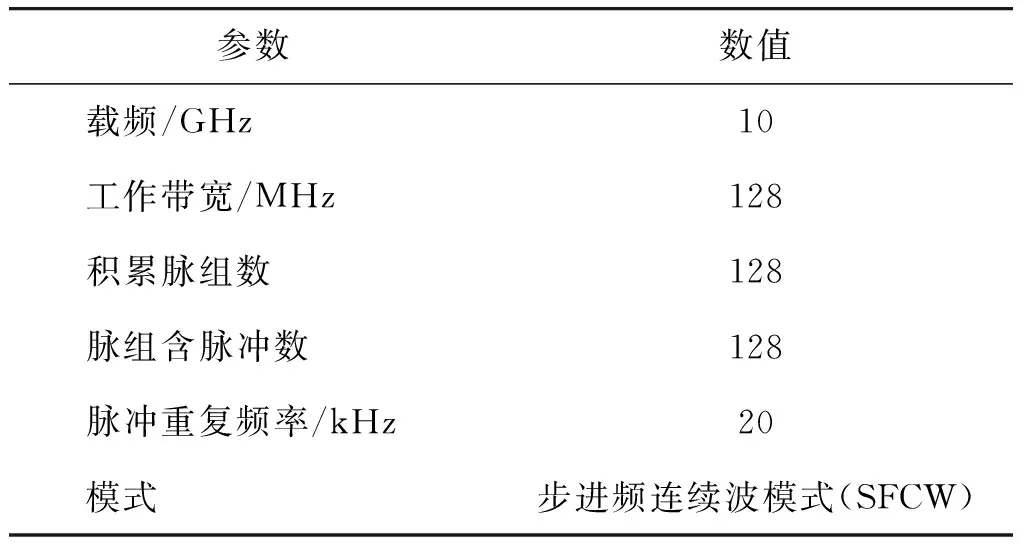
表2 雷达参数Table 2 Radar parameters

图2为对原始回波直接进行距离多普勒成像的结果，可见由于目标的高速运动，使得成像结果在距离多普勒平面内发生大范围模糊，各个散射点的跨距离方位单元走动严重；图3为原始的回波的包络图，可见同样由于目标的径向运动，相邻的一维距离像之间包络发生漂移，需要进行包络对齐校正。

图2 未进行运动补偿的距离多普勒图像图Fig.2 Uncompensated RD image

图3 原始图像的包络Fig.3 Uncompensated image’s range profile

3.2 简单模型仿真

按照式(3)计算各个一维距离像相对参考一维距离像的距离走动，然后将各个距离走动进行平滑后的结果，如图4所示，此时相邻一维距离像之间的距离走动如图5a)所示，可以看到相邻一维距离像之间的距离走动量恒定，将相邻一维距离像的距离走动差除以相邻距离像之间的时间间隔(脉冲重复周期)得到目标的速度，如图6b)所示，将速取平均得到估计平均速度为70.181 m/s，与真实目标速度70 m/s十分接近。

图4 距离走动和平滑后的结果图Fig.4 Range profile shifts and their smoothed results

图5 距离偏移差和径向速度Fig.5 Range differences and radial velocity

根据估计速度构造相位补偿函数对原始回波数据进行运动补偿后的回波包络图如图6a)所示，可以看到包络之间的距离走动完全消除，达到完全对齐效果，进行距离多普勒成像的结果如图6b)所示，可以看到图像轮廓清晰聚焦良好，相对于原始图像质量大大改善。

图6 包络对齐后的包络图和包络对齐后 的ISAR图像Fig.6 Range profile after alignment motion-compensated ISAR image

其他参数不变，更改目标径向运动速度为10 m/s得到的速度估计和平滑后相邻一维距离像的距离走动，如图7所示，补偿后的距离多普勒图像如图8所示，可以看到交叉相关法对低速运动目标同样有较准确的补偿效果。

图7 距离偏移差和径向速度Fig.7 Range differences and radial velocity

图8 包络对齐后的ISAR图像Fig.8 Motion-compensated ISAR image

经过更多仿真验证发现，在相邻包络相关系数平均值达到0.7以上时，交叉相关法的速度估计相对误差均值约为1%，在当前20 kHz重频等系统参数条件下，交叉相关法能估计速度的上限为100 m/s左右。当速度进一步提高，会导致相邻包络之间的距离走动量增加，相关性降低，进而降低交叉相关法的对齐效果，此时可以通过增加系统重频，插值等方法，提高脉间包络的相关性。

总之，经过仿真发现交叉相关法在速度不模糊范围内性能稳定，包络对齐效果良好，相对于其他算法，其速度估计精确度高，还可用于后续的目标定位跟踪。

3.3 噪声环境下仿真

为验证算法的稳健性，根据接收机的噪声统计特性，产生服从高斯分布的随机数模拟噪声，设置不同的信噪比，其他系统参数不变，设目标径向速度为10 m/s。

在信噪比为0 dB的情况下的仿真结果如图9，10所示。

在信噪比为-8 dB的情况下的仿真结果如图11，12所示。

图9 距离偏移差和径向速度Fig.9 Range differences and radial velocity

图10 包络对齐后的包络图和包络对齐后的ISAR图像Fig.10 Range profile after alignment motion-compensated ISAR image

图11 距离偏移差和径向速度Fig.11 Range differences and radial velocity

图12 包络对齐后的包络图和包络对齐后 的ISAR图像Fig.12 Range profile after alignment motion-compensated ISAR image

从仿真发现，交叉相关法可实现较低信噪比环境下的包络对齐。但是信噪比降低，实际上减小了相邻回波间的相关程度，使得速度估计误差变大，当信噪比减小到一定程度时，信号淹没在噪声中，回波之间的相关程度描述的实际是噪声的相关程度，基于相关法的包络对齐方法不能适用。

3.4 与相邻包络相关法的比较

相邻一维距离像的互相关系数可以代表包络对齐的程度，由于目标运动的机动性，未进行包络对齐的相邻包络之间相关系数波动较大，当包络对齐的效果较好时，相邻一维距离像的互相关系数较高，且较稳定，因此可以用相关系数衡量包络对齐的程度。设置目标径向速度为70 m/s，其他条件不变，原始回波相邻一维距离像的相关系数见图13a)，相邻包络相关法的相关系数见图13b)，交叉相关法相邻一维距离像的相关系数见图13c)。

图13 原始距离像和包络对齐后距离像相关系数Fig.13 Correlation coefficients of the original range profiles and the aligned range profiles

可以看到2种对齐方法都可以提高相邻距离像之间的相关程度，但是对比图13b)和c)可以发现，相邻包络相关法只是对相邻包络距离走动进行了校正，相对于原始距离像相关特性并没有发生变化，突跳误差没有得到消除，而交叉相关法对齐后相邻距离像相关程度更高，且相对于相邻相关法相关系数较稳定，没有明显的跳变，因此交叉相关法包络对齐效果更理想。更多组仿真实验可以得到相同结论。

4 结束语

本文从抑制包络对齐的3种误差出发，基于原有的相关对齐方法，提出一种新的包络对齐方法，该方法计算量小，对齐效果明显，且能适应低信噪比环境，仿真结果证明了本方法具有较强的工程应用价值。但是值得说明的是本方法适用于目标匀速运动的情况，对于变速运动目标，则需要在包络对齐后进行更高精度的运动补偿。

[1] CHEN C C，ANDREWS H C.Target-Motion-Induced Radar Imaging[J].IEEE Trans on AES，1980，16(1)：2-14.

[2] WANG J，KASILINGAM D.Global Range Alignment for ISAR[J].IEEE Trans on AES，2003，39(1)：351-357.

[3] LI X，LIU G，NI J.Auto Focusing of ISAR Images Based on Entropy Minimization[J].IEEE Trans on AES，1999，35(4)：1240-1251.

[4] 王琦，李亚超，邢孟道，等.多视角ISAR成像研究[J].西安电子科技大学学报，2007，34(2)：165-169. WANG Qi，LI Ya-chao，XING Meng-dao，et al.A Study of ISAR Imaging of Spatial Diversity Angles[J].Journal of Xidian University，2007，34(2)：165-169.

[5] 蒋楠稚，王毛路，李少洪，等.频率步进脉冲距离高分辨一维成像速度补偿分析[J].电子科学学刊，1999，21(5)：665-670. JIANG Nan-zhi，WANG Mao-lu，LI Shao-hong.Stepped Frequency Pulse Range High Resolution Imaging Velocity Compensation Analysis[J].Electrical Science Journal，1999，21(5)：665-670.

[6] PERRY R P，DIPIETRO R C，FANTE R L.SAR Imaging of Moving Targets[J].IEEE Trans on Aerospace.Electron.Syst.，1999，35(1)：188-199.

[7] DJURIC P M，KAY S M.Parameter Estimation of Chirp Signal[J].IEEE Trans.on Acoustics，Speech and Signal Processing，1990，38(12)：2118-2126.

[8] DELISLE G Y，WU H.Moving Target Imaging and Trajectory Computation Using ISAR[J].IEEE Trans on AES，1994，30(3)：887-899.

[9] 保铮，刑孟道，王彤.雷达成像技术[M].北京：电子工业出版社，2005. BAO Zheng，XING Meng-dao，WANG Tong.Radar Imaging Technique[M].Beijing：Publishing House of Electronics Industry，2005.

[10] XI L，LIU G，NI J.Autofocusing of ISAR Images Based on Entropy Minimization[J].IEEE Transactions on Aerospace & Electronic Systems，1999，35(4)：1240-1252.

[11] 余吉，许稼，汤俊，等.基于Keystone变换的改进雷达目标长时间积累[J].雷达科学与技术，2008，6(6)：454-458. YU Ji，XU Jia，TANG Jun，et al.An Improved Key-Stone-Transform Based Method for Long-Time Coherent Integration of Radar Target[J].Radar Science and Technology，2008，6(6)：454-458.

[12] THOMAS L M，ELIZABETH A M，CHARLES P P.Fast Pulse Doppler Radar Processing Accounting for Range Bin Migration[C]∥IEEE National Radar Conference，Lynnfield，MA，USA：[s.n.]，1993：264-268.

[13] RINEHART & AMP R E，GARVEY E T.Three-Dimensional Storm Motion Detection by Conventional Weather Radar[J].Nature，1978，273(5660)：287-289.

[14] LI L，SCHMID W，JOSS J．Now Casting of Motion and Growth of Precipitation with Radar Over a Complex Orography[J].Journal of Applied Meteorology，1995，34(6)：1286-1300．

[15] EVANS J E，DUCOT E R.The Integrated Terminal Weather System (ITWS)[J].Lincoln Laboratory Journal，1994，7(192)：449-474.

Fast Alignment Approach for ISAR Imaging Based on Cross Correlation

YAN Ya-qiong1，2，HE Zhi-yi2

(1.The Second Research Academy of CASIC，Beijing 100854，China；2.Beijing Institute of Remote Sensing Device，Beijing 100854，China)

Motion compensation is the first step of ISAR imaging,while envelope alignment is the first step of motion compensation, thus envelope alignment is the key point for the following procedures, such as Doppler tracking, cross-range scaling. Existing envelope alignment algorithms are mostly based on the correlation between adjacent envelopes which are liable for drift error, accumulation error and jump error. Analyzing the sources of the error, the cross-correlation technique is propased to solve the problem. Simulation results show that the new method is simple and effective with small amount of computation.

cross-correlation;envelop alignment；drift error；jump error；accumulation error；motion compensation；ISAR imaging

2016-08-10；

2016-10-18

有

闫雅琼(1988-)，女，河南三门峡人。博士生，主要研究方向为SAR/ISAR 成像运动补偿。

通信地址：100854 北京142信箱205分箱10号 E-mail：girlyanyaqiong@163.com

10.3969/j.issn.1009-086x.2017.03.018

TN951；TN911.73；TP391.9

A

1009-086X(2017)-03-0111-07