异类传感器动态数据关联算法*

惠军华，关冬冬，王朝英

(1.西安通信学院，陕西 西安 710106；2.空军工程大学 信息与导航学院，陕西 西安 710077 )

异类传感器动态数据关联算法*

惠军华1，关冬冬2，王朝英2

(1.西安通信学院，陕西 西安 710106；2.空军工程大学 信息与导航学院，陕西 西安 710077 )

数据关联是异类传感器系统中最核心且最重要的内容之一，典型的数据关联算法可以归结为特定的分配为问题，然而现有的S维分配算法只考虑同一时刻的每个传感器量测的互联。将此静态关联推广到动态关联中，提出了一种适用于异类传感器的(S+1)维动态数据关联算法。该算法首先将同一时刻各传感器的量测与目标轨迹的一步预测值合并，把问题转化为(S+1)维分配问题，然后将各传感器量测估计的位置信息与目标航迹的预测值的差值作为关联代价，并利用LP-SOLVE工具包解决多维分配问题，最后利用求得的全局最优关联解进行滤波和航迹的更新。仿真实验表明提出的关联代价能更精准地反映数据关联的可能性，能够对多目标进行稳定的跟踪。

异类传感器；动态数据关联；多维分配；LP-SOLVE 工具包；代价函数；多目标跟踪

0 引言

异类传感器信息融合系统[1]能够将主、被动传感器配合使用，充分利用主动传感器较精准的距离量测与被动传感器较精准的角度量测，可兼顾二者的优势，必在未来战争中发挥不可替代的作用。

数据关联问题一直是目标跟踪融合系统中最重要、最困难的研究内容[2-3]，而现今已有的数据关联算法多是针对有源传感器提出的，其中最经典的算法是联合概率数据互联算法(joint probabilistic data association，JPDA)、多假设方法(multiple hypothesis tracking algorithms，MHT)和多维分配算法(more dimension，S-D)。JPDA[4]通过计算落入确认门内的多个测量与该航迹互联的概率，并利用该概率和相伴的测量对目标的状态进行估计。MHT算法[5]通过枚举在一定时间深度下可能的量测与航迹互联的假设，并计算相伴的概率，在一定的准则下得到目标的状态估计。但MHT的计算量极大，呈指数增长甚至造成计算量的爆炸，因而实际中必须对搜索进行限制。(S-D)[5-8]的数据关联问题，实质上是在一定约束条件下的最优化问题。Kirubarajan。提出了一种新的2D分配算法，用来解决一对多或多对一的分配问题。这一问题的解决，突破了一对一分配的限制，使得最近邻、联合概率数据互联、多假设等典型的数据关联算法都可以归结为多维分配的问题。文献[9]针对多传感器多目标跟踪问题提出了动态多维分配算法，将静态分配推广到动态跟踪中，通过对测量集合和航迹集合的合并，把S维转变为S+1维问题，从而实现了分配的动态化。

而针对异类传感器融合系统提出的数据关联算法涉及较少，本文建立了异类传感器融合系统多维分配数据关联的框架，实现了异类传感器多目标跟踪。以3D雷达和红外传感器组成的异类传感器信息融合系统为例，提出了异类传感器动态关联模型，并阐述了(S+1)维多维分配的动态关联算法，充分利用3D雷达较精确的距离量测信息与红外传感器较精确的角度量测信息，将各观测向量组合起来构造成高维观测向量，运用最小二乘进行位置估计，再与目标航迹的预测值做差构造代价函数，进行多维分配，从而求得全局最优。最后利用仿真实验验证了算法的有效性。

1 异类传感器关联问题描述

为简单描述起见，以图1所示的1部3D雷达和2部红外传感器组成的异类传感器融合系统同步扫描探测为例，考虑漏检和虚警，建立了异类传感器数据关联问题模型。

图1 3D雷达与红外传感器协同观测模型Fig.1 Cooperative observation model of 3D radar and infrared sensor

3D雷达量测目标j的距离记为r1j，方位角记为β1j和仰角记为α1j，分别表示如下[10]：

(1)

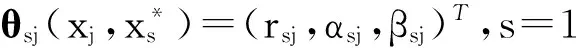
红外传感器只有角度信息，目标j的方位角为βsj、仰角为αsj，分别为

(2)

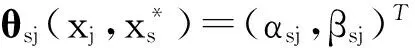
综上，传感器的量测模型为

msj=

(3)

传感器s的ns个量测中，来自真实目标的量测为真实目标的位置加上高斯噪声，即vsj，服从高斯分布vsj～N(0，Rsj)，来自虚警的量测在空间中无规律分布，视为均匀分布，概率密度wsj=1/Φs(0<Φs<π2)。

为使得所有量测数据均参与关联，给每个传感器s增加一个虚假量测ms0，则传感器s获得的量测集合为

(4)

并记所有传感器获得的量测数据为

(5)

为实现跟踪，必须将量测与目标航迹建立联系。把k时刻来自S个传感器的量测集合与k时刻系统的目标航迹的预测值集合合并，表示为

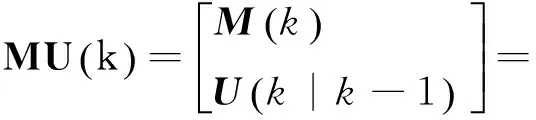
(6)

2 基于(S+1)维多维分配的动态关联算法

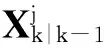
2.1 位置统计特性分析

基于伪线性估计[11]的思想，式(1)可化为

(7)

(8)

(9)

同理，式(2)的估计同式(8)，(9)，式中s=1，2，3。

将3个传感器的量测转化为矩阵的形式如下：

Hxi=Y，

(10)

式中：

(11)

(12)

则待求目标的位置估计值为

(13)

其对应的方差为

(14)

式中：

(15)

(16)

将式(11)，(15)带入式(14)，即可得到伪量测的方差信息。

进一步提高定位的精度，还可采用文献[12]提出的快速定位方法。

2.2 动态多维分配目标函数构造

(17)

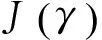
(18)

(19)

(20)

(21)

(22)

(23)

2.3 多维分配求解分析

当基站数大于(等于)3个时，数据关联的问题即为多维分配问题，多维分配问题的计算是一个极其复杂的问题，其计算复杂度随着传感器和目标的数量的增加呈指数增长。目前主流算法是运用拉格朗日松弛法进行降维处理，将三维分配问题转化成二维，求解最优解[14]。后有学者提出了基于代理次梯度的拉格朗日松弛法，针对多维分配中基于次梯度算法的拉格朗日松弛算法每次迭代都要对每个子问题进行最小化运算以更新乘子的缺陷，引入代理次梯度，修改次梯度表达式和乘子更新公式，该方法在大规模问题下可以节约计算时间，降低跟踪丢失率[15]。

对于上述多维分配问题，本文采用离线工具包LP_SOLVE[16-17]进行求解。该软件包可以在多种语言环境下运行，易于调用加载，具有良好的稳健性，而且其计算效率较高，对于高维问题亦可以有效解决，特别适用于工程开发。

2.4 算法流程

在获得最优关联方案后，将其对应的各传感器量测直接用于航迹更新，从而为下一时刻的量测-航迹的关联提供新的先验信息。

异类传感器多目标数据关联算法步骤如下：

(1) 利用卡尔曼滤波对目标的状态进行估计，得出各时刻目标位置的预测信息；

(2) 分别在各传感器量测集合中任意选取量测进行最小二乘位置估计；

(3) 利用传感器量测得出的位置估计与目标位置的预测信息做差，构成代价函数；

(4) 通过构建动态多维分配模型得到最优关联方案，并将其对应的各传感器量测分配给相应的目标用于航迹更新。

三维平面内异类传感器系统数据关联算法流程如图2所示。

图2 异类传感器数据关联算法流程图Fig.2 Flow chart of heterogeneous sensor data association algorithm

3 实验结果分析

分别在三维平面内3个目标平行运动及交叉运动不同场景下进行仿真验证。假设三维平面内，3D雷达的位置坐标为(20，0，0.1)km，2个红外传感器的坐标分别为(0，10，1)km和(0，0，0.5)km。设定传感器的采样周期为T=1 s，蒙特卡罗试验次数为100。

场景1：目标平行运动

3个目标的初始位置分别为目标1：(40，30，5)km，目标2：(45，30，5)km，目标3：(50，30，5)km。3个目标均做匀速直线运动，其速度均为vx=200 m/s，vy=50 m/s，vz=100 m/s。图3给出了传感器的量测误差标准差σ分别为10，15，20 mrad时3个目标的真实运动轨迹以及经过1次蒙特卡罗仿真实验的滤波结果，图4给出了传感器的量测误差标准差σ分别为10，15，20 mrad时3个目标的均方根误差，蒙特卡洛仿真次数为100。

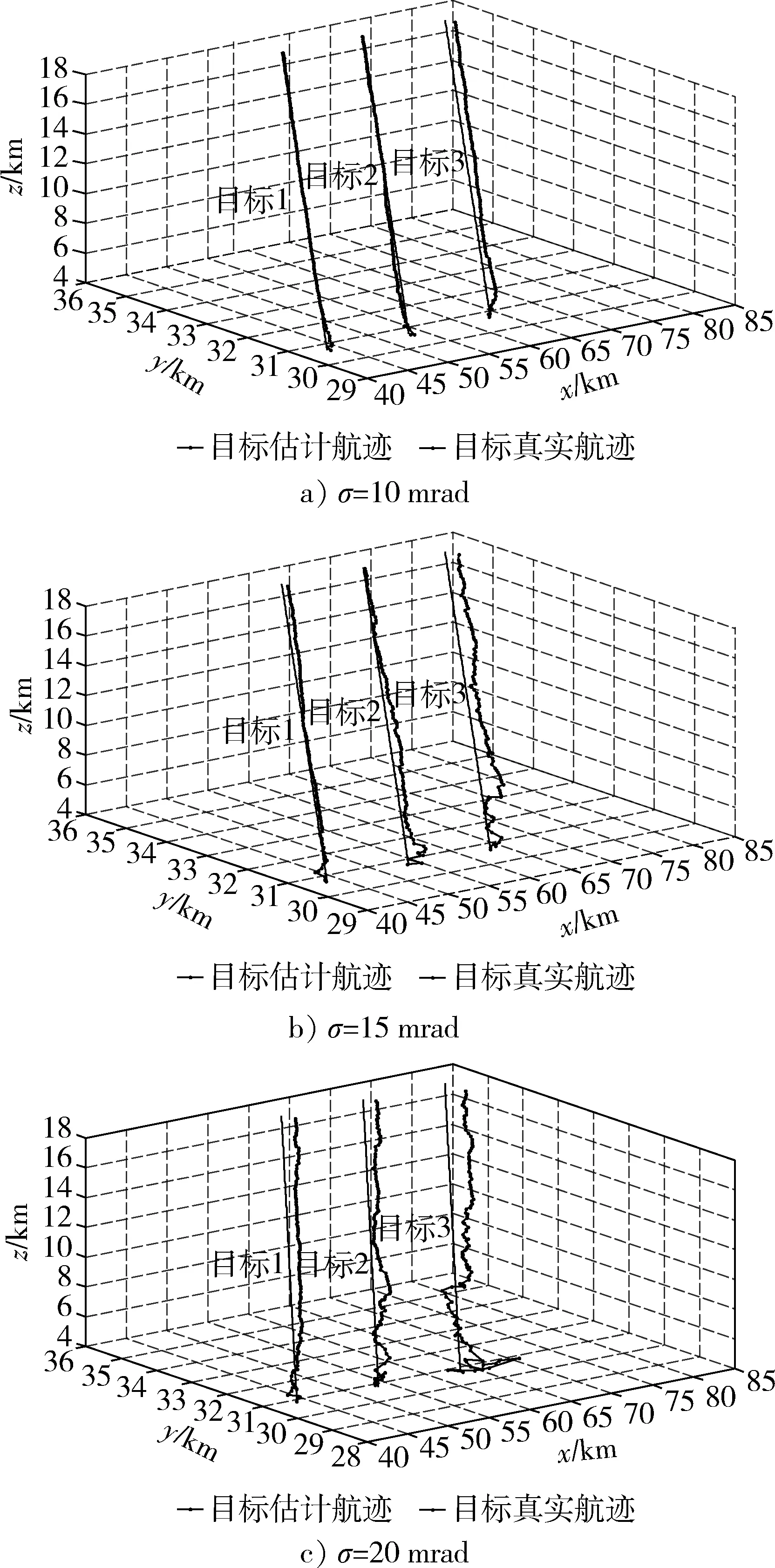
图3 三平行目标在不同传感器量测误差下的真实轨迹及估计轨迹Fig.3 Real trajectory and estimated trajectory of three parallel targets under different sensor measurement errors

图4 三平行目标在不同传感器量测误差下的跟踪均方根误差Fig.4 Tracking root mean square error of threeparallel targets under different sensor measurement errors

由以上仿真结果可以看出，采用动态多维分配方法能够对平行匀速直线运动的目标进行较为稳定的跟踪，并且随着传感器的量测误差标准差σ增大，跟踪效率有所下降，但跟踪均方误差仍旧比较低。

图5给出了传感器在不同量测误差条件下目标在间距分别为d=5 km和d=10 km下的采用动态多维分配算法进行数据关联时得到的平均正确关联概率的比较结果。

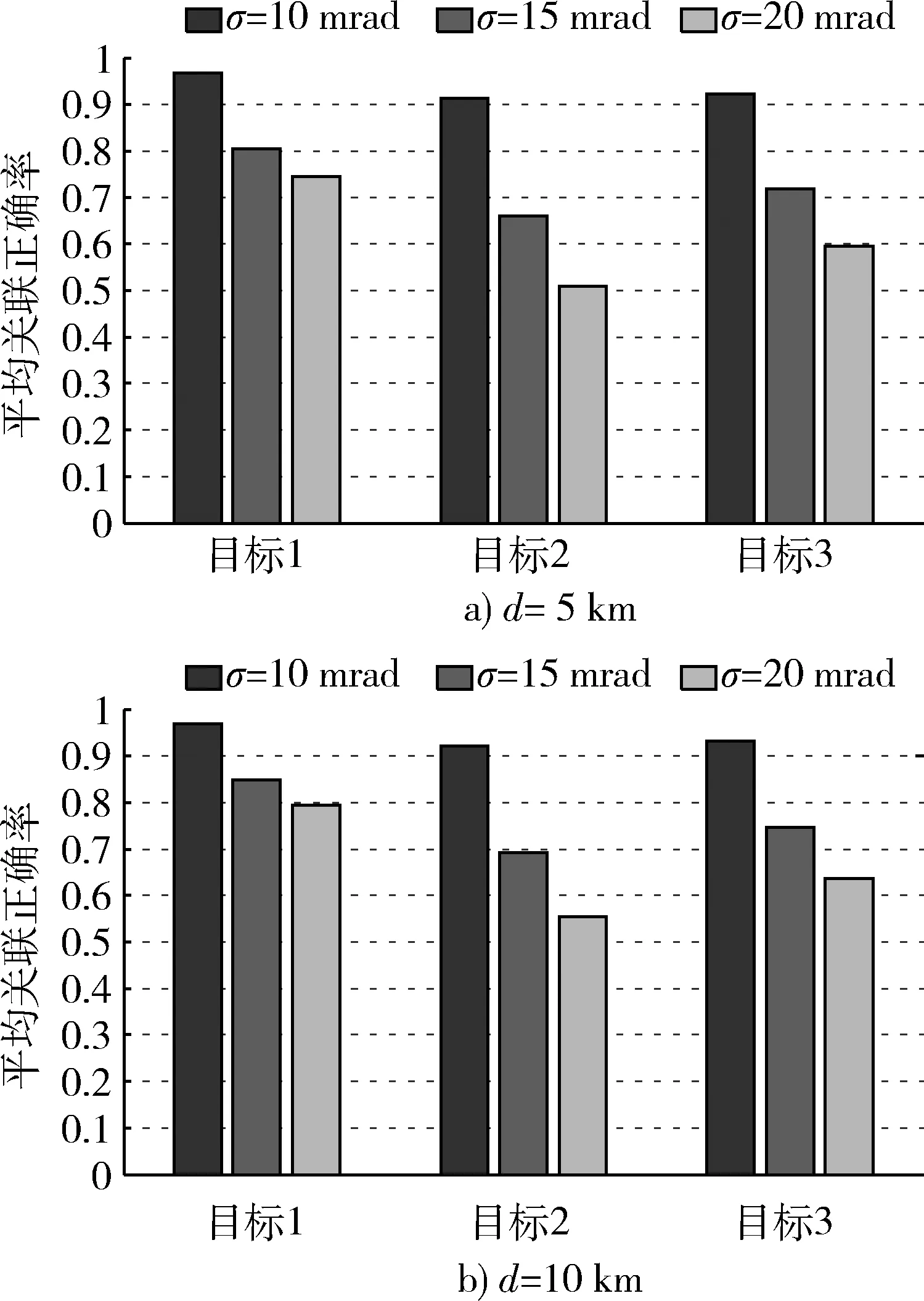
图5 三平行目标在不同间距不同传感器量测误差下的关联正确率比较Fig.5 Comparison of correlation accuracy of three parallel targets under different measurement errors of different distances

从上述柱状图可以看出，在目标间距一定的条件下，随着传感器量测误差的增大，平均关联正确率逐渐降低。

表1给出在不同传感器量测与不同目标间距的情况下，采用动态多维分配算法进行数据关联时得到的平均正确关联概率的比较结果。

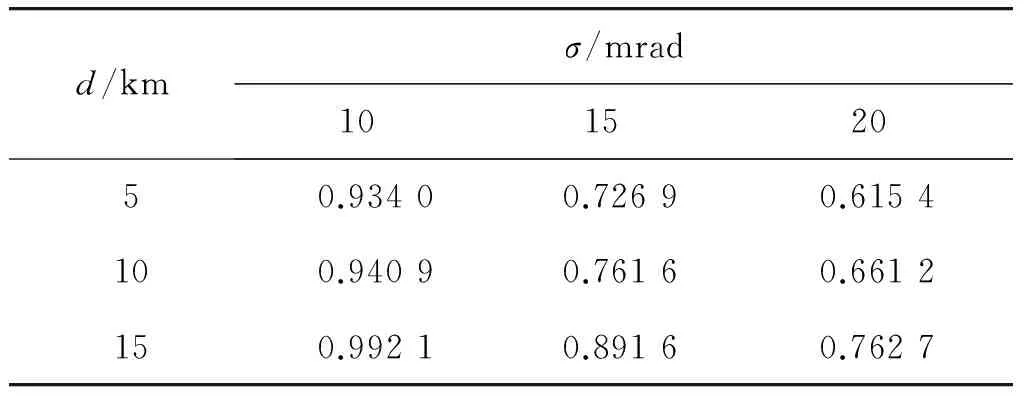
表1 三平行目标在不同传感器量测误差下 的跟踪均方根误差Table 1 Tracking root mean square error of three parallel targets under different sensor measurement errors

通过分析表1中的数据，除了可以得出传感器量测误差相同时，目标间距越大，平均关联正确率越高的结论外，还可以看出，在相同的传感器量测误差下，目标间距越大，平均关联正确率增加。

场景2：目标交叉运动

3个目标的初始位置分别为目标1：(40，30，5)km，目标2：(45，30，5)km，目标3：(60，30，5)km。3个目标均作匀速直线运动，速度如表2所示。

图6给出了传感器的量测误差标准差σ分别为10，15，20 mrad时3个目标的真实运动轨迹以及经过1次蒙特卡罗仿真实验的滤波结果。图7给出了传感器的量测误差标准差σ分别为10，15，20 mrad时3个目标的均方根误差，蒙特卡罗仿真次数为100。

表2 三交叉目标运动速度Table 2 Three cross targets speed error (m·s-1)

图6 三交叉目标在不同传感器量测误差下的真实轨迹及估计轨迹Fig.6 Real trajectory and estimated trajectory of three cross targets under different sensor measurement errors

图7 三交叉目标在不同传感器量测误差下的跟踪均方根误差Fig.7 Tracking root mean square error of three cross targets under different sensor measurement errors

综合上述实验的结果可以看出，3个匀速运动的目标在3D空间内交叉运动，跟踪均方误差随着传感器两侧误差的增加有所增高，但总体上保持在一个比较低的水平。

图8给出了传感器在不同量测误差条件下采用动态多维分配算法进行数据关联时得到的平均正确关联概率的比较结果。

图8 三交叉目标在不同传感器量测误差下的关联正确率比较Fig.8 Comparison of correlation accuracy of three cross targets under different sensor measurement errors

可以看出，随着传感器量测误差的增加，平均关联正确率有所下降。总体来说，动态多维分配方法对平行运动目标与交叉运动目标均具有比较好的关联效果。

4 结束语

本文针对三维空间中3D雷达与红外传感器组成的异类传感器系统的动态数据关联问题进行了研究，将(S+1)维多维分配算法用于异类传感器数据关联系统。首先连接具有共同源的量测或轨迹，组成关联集合，再运用定位算法得出传感器量测估计的目标位置，与目标的预测位置进行关联，得到全局最优的关联结果，从而更新航迹。

动态数据关联作为一个最优化问题，与静态数据关联相比多了一维，本文运用的(S+1)维多维分配算法，从数学角度看保证了全局最优。另一方面，在静态关联领域内对多维分配算法的改进、优化，都可以直接运用于本文的多维分配模型中，具有很好的可扩展性，有较大的改进余地。

[1] 王国宏，毛士艺，何友．雷达与红外数据融合评述[J]．火力与指挥控制，2002，27(2)：3-6． WANG Guo-hong，MAO Shi-yi，HE You.A Survey of Radar and Infrared Data Fusion[J].Fire Control & Command Control，2002，27(2)：3-6.

[2] 何友，王国宏，彭应宁.多传感器信息融合及应用[M].3版．北京：电子工业出版社，2007． HE You，WANG Guo-hong，PENG Ying-ning.Multiple Sensor Information Fusion and Application[M]3ed.Beijing:Publishing House of Electronic Industry，2007.

[3] 赵域，张剑云，戴定川.主/被动雷达情报协同浅议[J].飞航导弹，2011(3)：87-90. ZHAO Yu，ZHANG Jian-yun，DAI Ding-chuan.Master/Passive Radar Intelligence Synergistic Extraction[J].Aeroynamic Missile Journal，2011(3)：87-90.

[4] BAR-SHALOM Y，Thomas E Fortmann.Tracking and Data Association[M].Oriando，FL：Academic Press，1988.

[5] Donald B Reid.An Algorithm for Tracking Multiple Targets[J].IEEE TransAC，1979(24)：843-854.

[6] BAR-SHALOM Y，LI Xiao-rong.Multitarget-Multisensor Tracking，Principle and Techniques[M].Norwood，MA：Artech House，1995.

[7] ROECHER J A，PHLILLS G L.Suboptimal Joint Probabilistec Data Association[J].IEEE Transation on AES.1993，29(2)：510-517.

[8] BAR-SHALOM Y，WILLIAM D B.Multitarget-Multisensor Tracking，Applications and Advances[M].Norwood，MA：Artech House，2001.

[9] 衣晓，何友，关欣.多目标跟踪的动态多维分配算法[J].电子学报，2005，33(6)：1120-1123. YI Xiao，HE You，GUAN Xin.Dynamic Multidimensional Assignment Algorithm for Multitarget Tracking[J].Acta Electronia Sinica，2005，33(6)：1120-1123.

[10] 李彬彬，冯新喜，王朝英，等.异类传感器三维空间数据关联算法研究[J]．宇航学报，2011，32(7)：1632-1638． LI Bin-bin，FENG Xin-xi，WANG Zhao-ying，et al.Data Association Algorithm for Three-Dimensional Heterogeneous Sensors[J].Journal of Astronautics，2011，32(7)：1632-1638．

[11] 王鼎，张莉，吴英.基于角度信息的约束总体最小二乘无源定位算法[J].中国科学E辑信息科学，2006，36(8)：880-890. WANG Ding，ZHANG Li，WU Ying.Based on the Constraint Information from the Angle of Overall Least-Square Passive Location Algorithm[J].Science China Series Information Sciences，2006，36(8)：880-890.

[12] 刘宗香，黄静雄，杨烜，等.异类传感器系统目标快速定位方法[J].系统工程与电子技术，2007，29(12)：2010-2014． LIU Zong-xiang，HUANG Jing-xiong，YANG Xuan，et al.Fast Target Location Method in the Heterogeneous Sensor System[J].Systems Engineering and Electronics，2007，29(12)：2010-2014．

[13] Somnath Deb，Krishna R Pattipati，Yaakov Bar-Shalom.A Multisensor-Multitarget Data Association Algorithm for Heterogeneous Sensors[J].IEEE Transactions on Aerospace and Electronic Systems，1993，29(2)：560-568．

[14] PATDPATI K R，DEB S，BAR-SHALOM.A New Relaxation Algorithm and Passive Sensor Data Association[J].IEEE Transaction on Automatic Control，1992，37(1)：198-213.

[15] 王以标，徐毓，张云龙.基于广义三维分配的数据互联算法研究[J].现代防御技术，2009，37(3)：122-126. WANG Yi-biao，XU Yu，ZHANG Yun-long.Study on Generalized 3-D Distribution Based Data Association Algorithm[J].Modern Defencb Technology，2009，37(3)：122-126.

[16] Sunsil Mathews.An Efficient Implementation of a Batch-Oriented，Multitarget，Multidimensional Assiganment Tracking Algorithm with Application to Passive Sonar[R].Naval Undersea Warfare Center Division Newport，Rhode Island，NUWC-NPT Technical Document 12036，2011.

[17] BERKELAAR M，EIKLAND K，NOTEBAERT P.Introduction to Lp_Solve5.5.2.0.[CP].http：∥lpsolve.sourceforge.net/5.5/，2004.

Dynamic Data Association Algorithm for Heterogeneous Sensors

HUI Jun-hua1，GUAN Dong-dong2，WANG Zhao-ying2

(1.Xi’an Communications Institute，Shaanxi Xi’an 710106,China；2.Airforce Engineering University，Information and Navigation Institute，Shaanxi Xi’an 710077，China)

Data association is one of the most important and the most primary contents in heterogeneous sensor systems. A typical data association algorithm can be formulated as a special assignment problem. However, the existingS-D (S Dimensions) assignment algorithm only considers the interconnection of each sensor at the same time. The staticS-D assignment algorithm is extended into the dynamicS-D assignment algorithm，and a dynamic (S+1)D data association algorithm for heterogeneous sensor systems is proposed.In this algorithm, firstly the measurement of each sensor at the same time is combined with one step prediction value of the target trajectory, and the problem is transformed into a (S+1) -dimensional assignment problem, then the difference between the estimated position information of each sensor and the predicted value of the target track is taken as the associated cost, and theS-D assignment problem is solved by using the LP-SOLVE toolkit, finally the global optimal solution is used to filter and updating the track. The results show that the cost function can reflect the association probability more accurately and can steadily track multiple targets.

heterogeneous sensors；dynamic data association；multidimensional assignment；LP-SOLVE toolkit；association cost；multitarget track

2016-07-10；

2016-09-20

惠军华(1990-)，女，陕西西安人。讲师，硕士，主要研究方向为多源信息融合。

10.3969/j.issn.1009-086x.2017.03.031

TN953；TP301.6

A

1009-086X(2017)-03-0200-08

通信地址：710106 陕西省西安市长安区王曲镇西安通信学院 信息服务系 信息资源管理教研室

E-mail：1011009123@163.com