微小型飞行器多传感器融合容积姿态估计*

石章松，吴中红，刘健，傅冰

(海军工程大学 电子工程学院，湖北 武汉 430033)

微小型飞行器多传感器融合容积姿态估计*

石章松，吴中红，刘健，傅冰

(海军工程大学 电子工程学院，湖北 武汉 430033)

针对微机电系统(MEMs)陀螺仪精度低、噪声大且误差随时间累积的问题，扩展卡尔曼滤波(EKF)线性化误差的问题和无迹卡尔曼滤波(UKF)时间耗费大的问题，提出了一种欧拉角容积卡尔曼滤波(CKF)姿态估计方法。建立了欧拉角姿态运动学模型，以姿态角为状态量、加速度计和磁强计输出解算得到的姿态角为观测量，采用容积数值积分理论来计算非线性函数的均值与方差，实现了多传感器辅助的微小型飞行器(MAVs) CKF姿态估计方法。仿真结果表明：估计精度方面，CKF与UKF相当，优于EKF；滤波稳定性方面，CKF与UKF相当，显著优于EKF；时间耗费方面，CKF优于UKF。

非线性滤波；容积卡尔曼滤波；欧拉角；多传感器；姿态估计；微小型飞行器

0 引言

姿态参数是微小型飞行器MAVs实现稳定飞行的关键参数之一[1-2]。MAVs载荷较轻，不适合搭载光纤/激光姿态测量系统，通常搭载微机电系统MEMS陀螺仪进行姿态测量。MEMS陀螺仪动态性能良好，但是精度低、噪声大，且其测量误差会随着时间积累，不适合长时间载体姿态确定。而测量重力场分量的加速度计与测量地磁场分量的磁强计则具有良好的静态性能，不存在误差积累问题，但是易受载体机动、外部磁场影响，从而导致动态性能下降[3]。将陀螺仪、加速度计以及磁强计的数据进行融合处理，则能够发挥加速度计与磁强计的静态优点，对陀螺仪动态误差进行补偿，从而有效提高姿态测量的精度。

文献[4-5]分别开展了将重力场与地磁场数据辅助MEMS器件进行姿态估计的研究，应用扩展卡尔曼滤波EKF[6-7]实现了对姿态参数的估计。通过对非线性系统的一阶线性化近似，EKF能够较好地处理一般的非线性系统，但是由于忽略了系统的部分非线性特性，当系统的非线性特性较为突出、初始误差较大时，EKF存在估计效果急剧下降和滤波收敛速度缓慢的问题，不能达到可靠的估计效果[8]。而无迹卡尔曼滤波UKF[9-10]采用无迹变换进行随机变量传播，以获取更为准确的非线性函数概率分布，能够更好地应对非线性特征明显的非线性系统估计问题[11]，文献[12]将UKF方法引入到姿态估计中，克服了EKF在姿态估计中的线性化误差问题，提高了姿态估计的精度。

但是UKF需要对3个可调参数进行适当选择才能达到良好的滤波相关，且需要2n+1个采样点，收敛时间相比于EKF有一定的增加[12]，在工程实现上存在限制[13]。而容积卡尔曼滤波CKF[14]使用一组等权值的容积点集来计算非线性变换后的随机变量的均值和协方差，具有更优的非线性逼近性能(三阶矩)、数值精度以及滤波稳定性，同时具有实现简单、运算时间短的特点，目前广泛应用于数据融合[15]、姿态估计[16]以及移动机器人位姿估计[17]问题中。

针对UKF存在的滤波稳定性较差、耗时较长以及参数设置困难等问题，本文在文献[12]的基础上，将CKF引入到基于欧拉角描述的姿态估计中，将陀螺仪、加速度计以及磁强计的数据融合处理，在保证相同滤波精度的前提下，提高了滤波稳定性，降低了估计耗时。

1 系统建模

1.1 多传感器测量结构

多传感器测量结构由陀螺仪、加速度计和磁强计组成，如图1所示。陀螺仪输出的角速率信息可以通过积分获得载体姿态，具有很好的动态性能和短时精度，但是精度较低，姿态误差随时间积累很快；加速度计则可以通过感知重力加速度在其测量轴上分量的大小来确定载体的姿态角，具有很好的长期稳定性，但是受载体机动加速度影响严重；磁强计则能测得地磁场在载体坐标系的投影。采用CKF对上述数据进行融合，可以获得静态漂移和动态特性均较好的姿态估计[18-19]。

图1 多传感器测量结构Fig.1 Multi-sensor measurement structure

1.2 状态方程

常见的姿态运动学模型主要有欧拉角、四元数以及罗德里格斯参数等。其中欧拉角法具有简便直观、物理含义明确的优点，且不存在冗余参数，虽然在俯仰角为90°时存在奇异，但对MAVs而言，俯仰角基本不会到达90°，因此本文采用欧拉角法对姿态运动学进行描述来建立状态方程。取状态向量为

(1)

式中：φ，θ，γ分别为偏航角、俯仰角、滚动角。

设陀螺仪输出的角速度为(ωb，x，ωb，y，ωb，z)T，则有

(2)

考虑常值误差和测量噪声，式(2)变为

(3)

式中：v1，v2，v3为陀螺输出数据中的测量噪声。

又

(4)

将式(3)带入式(4)，可得状态方程为

(5)

1.3 量测方程

基于双向量法建立量测方程[20]。首先，通过重力向量求解滚转角φ 和俯仰角θ 。通常认为在导航系下，重力向量是不变的，可以表示为gn=(0，0，g)T，其中g为当地重力加速度。记载体坐标系下的重力向量为gb=(gbx，gby，gbz)T，则有

(7)

则由式(6)可得滚转角φk、俯仰角θk为

(8)

然后，基于磁强计的输出得到偏航角ψk为

(9)

式中：Hb=(Hbx，Hby，Hbz)T为磁强计的输出值。

综合式(8)，(9)根据加速度计与磁强计的输出，可得量测方程为

(10)

式中：wk为量测噪声，其均值为0且方差为Rk。

2 容积卡尔曼滤波方法

假设一个非线性系统：

(11)

式中：xk∈Rn为k 时刻系统的状态向量；zk∈Rm为k时刻系统的观测向量；wk为均值为0、协方差为Qk的n 维随机过程噪声；vk为均值为0、协方差为Rk的m 维随机量测噪声，且wk，vk互不相关。CKF通过三阶容积积分原理，计算函数的标准加权高斯积分[15]。标准的CKF步骤如下：

(1) 初始化

(12)

(2) 时间更新

1) 设k-1时刻协方差矩阵Pk-1|k-1正定，对其进行因式分解得到Sk-1|k-1，即

(13)

2) 容积点估计

(14)

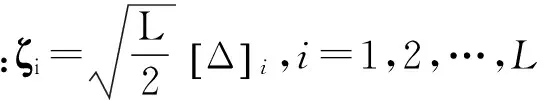
3) 容积点传播

(15)

4) 求解状态一步预测值

(16)

5) 计算预测误差协方差矩阵

(17)

(3) 量测更新

1) 预测误差协方差矩阵分解

(18)

2) 容积点估计

(19)

3) 容积点传播

(20)

4) 计算量测预测值

(21)

(22)

(23)

(4) 状态更新

1) 求解Kalman增益

(24)

(25)

3 仿真校验

通过计算机仿真对文中方法的有效性进行验证。仿真参数：状态初始值为x0=(0，0，0)T，MAV的角速度为ω=(0.05，0.05，0.05)Trad/s，陀螺仪采样间隔为0.1s，初始估计的误差协方差矩阵为P0=diag(1，1，1)，过程噪声协方差矩阵Qk=diag(0.0012，0.0012，0.0012)，量测噪声协方差矩阵为Rk=diag(0.0052，0.0052，0.0052)，100次MonteCarlo仿真的均值结果如图2～4以及表1～4所示。

从估计精度、滤波稳定性以及运算耗时3个方面对仿真结果进行分析。

图2，3和表1，2反映了不同滤波方法的估计精度。可以看出，CKF的估计精度与UKF估计精度基本一致，均优于EKF，以估计误差MonteCarlo仿真绝对均值进行比较，在滚转角、俯仰角和偏航角3个维度上相比于EKF分别提高约15.8%，16.8%，19.8%，以估计误差均方差MonteCarlo仿真均值比较，则分别提高29.7%，28.7%，30.7%。

图2 100次Monte Carlo仿真估计误差均值比较Fig.2 Comparison of estimation mean error of 100 Monte Carlo simulations with different filters

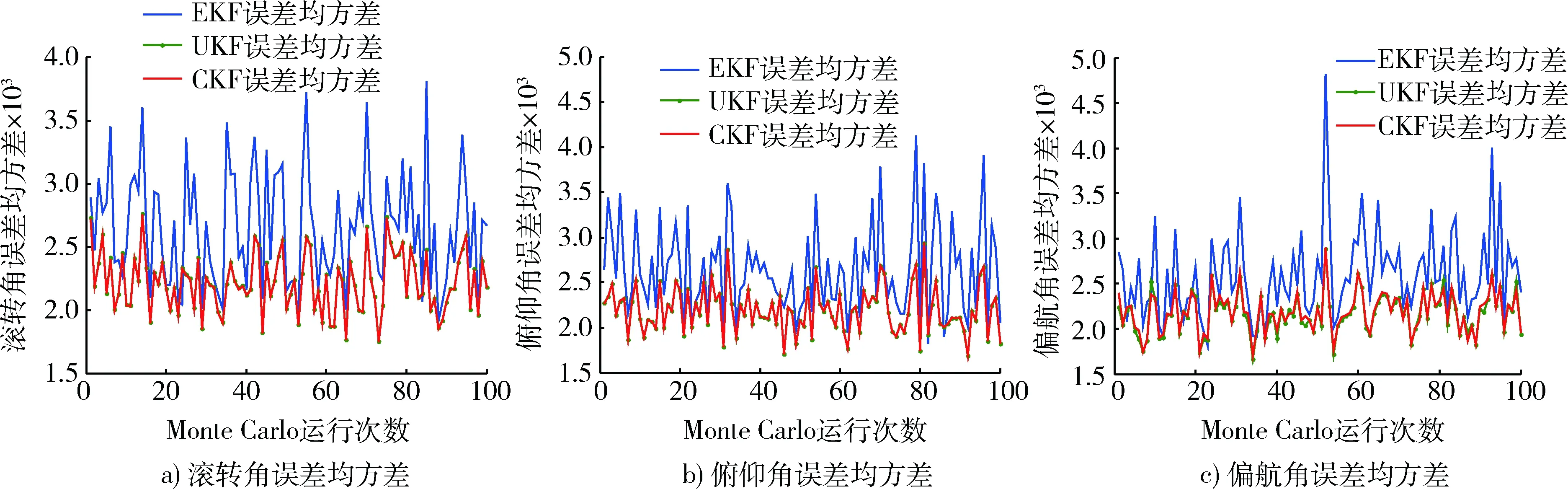
图3 100次Monte Carlo仿真估计误差均方差比较Fig.3 Comparison of mean square error of 100 Monte Carlo simulations with different filters

图4、表3反映了不同滤波方法的滤波稳定性。采用归一化方差(normalizederrorsquared，NES)指标进行比较：

表1 欧拉角的估计误差绝对均值Table 1 Absolute mean value of the estimation error of Euler angle mrad

表2 欧拉角的估计均方差均值Table 2 Mean value of the estimation mean square error of Euler angle mrad

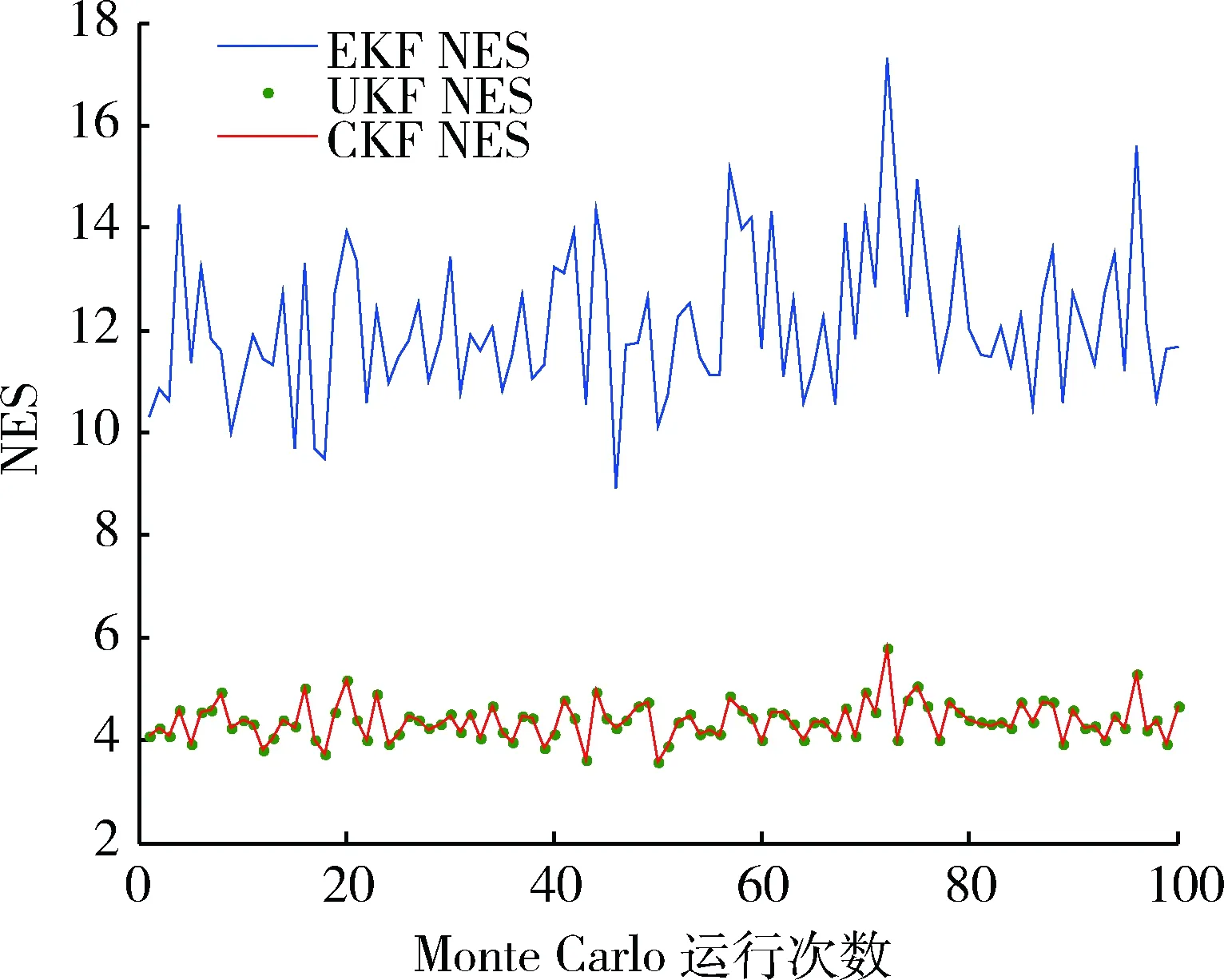
图4 100次Monte Carlo仿真NES指标对比Fig.4 Comparison of 100 Monte Carlo simulations with NES index

算法EKFUKFCKFNES均值(MNES)12.10654.37794.3818

表4 100次Monte Carlo仿真耗时Table 4 Time cost of 100 Monte Carlo simulations s

NES 指标反映滤波的稳定性和一致性，当 NES 指标的数值越接近估计状态量的维数(本文中状态量维数为 3)，说明该滤波算法的稳定性和一致性越好。仿真结果显示，CKF与UKF的稳定性相一致，均明显优于EKF。

表4显示了不同滤波方法的运算耗时。EKF的运算效率最优，CKF次之，UKF最差，其中CKF为EKF耗时的1.474倍，UKF为EKF的1.730倍，但CKF单次运算周期为0.096 s，支持150 Hz以上的姿态角更新，满足MAVs姿态估计实时性要求。

4 结论

(1) 估计精度方面，CKF与UKF相当，均优于EKF，以估计误差为指标进行比较，CKF在滚转角、俯仰角和偏航角3个维度上相比EKF分别提高了15.8%，16.8%，19.8%，以误差均方差做指标进行比较，则分别提高了29.7%，28.7%，30.7%；

(2) 滤波稳定性与一致性方面，以NES为指标进行比较，CKF与UKF相当，均显著优于EKF；

(3)时间耗费方面，CKF劣于EKF，但优于UKF，其中CKF为EKF耗时的1.474倍，为UKF耗时的0.816倍，尽管劣于EKF，但单次解算周期仅为0.096 s，支持150 Hz以上的姿态角更新，满足MAVs姿态估计实时性要求。

[1] 周婧，高印寒，刘长英，等.基于自适应算法的单目视觉系统的姿态解算[J].光学精密工程，2012，20(12)：2796-2803. ZHOU Jing，GAO Yin-han，LIU Chang-ying，et al.Attitude Calculation of Single Camera Visual System Based on Adaptive Algorithm[J].Optics and Precision Engineering，2012，20(12)：2796-2803.

[2] 王琳，何昕，魏仲慧.采用多站图像直线特征的飞机姿态估计[J].光学精密工程，2013，21(7)：1831-1839. WANG Lin，HE Xin，WEI Zhong-hui.Attitude Estimation of Aircrafts Using Line Features on Multi-Camera Images[J].Optics and Precision Engineering，2013，21(7)：1831-1839.

[3] 宋英麟，鲜斌，茹滨超，等.无人机微型姿态航向系统数据处理[J].中南大学学报：自然科学版，2013，44(Sl2)：89-93. SONG Ying-lin，XIAN Bin，RU Bin-chao，et al.Micro Attitude and Heading Reference System for Unmanned Aerial Vehicles[J].Journal of Central South University：Nature Science ed,2013，44(Sl2)：89-93.

[4] 张欣，白越，赵常均，等.多旋翼姿态解算中的改进自适应扩展Kalman算法[J].光学精密工程，2014，22(12)：3384-3390. ZHANG Xin，BAI Yue，ZHAO Chang-jun，et al.Improved Adaptive Extended Kalman Algorithm for Attitude Estimation of Multi-Rotor UAV[J].Optics and Precision Engineering，2014，22(12)：3384-3390.

[5] 宋宇，翁新武，郭昕刚.基于四元数EKF算法的小型无人机姿态估计[J].吉林大学学报:理学版，2015，53(3)：511-518. SONG Yu，WENG Xin-wu，GUO Xin-gang.Small UAV Attitude Estimation Based on the Algorithm of Quaternion Extended Kalman Filter[J].Journal of Jilin University:Science Edition ed，2015，53(3)：511-518.

[6] ASADIAN A，KERMANI M R，PATEL R V.A Novel Force Modeling Scheme for Needle Insertion Using Multiple Kalman Filters [J].IEEE Trans.Instrum.Meas.，2012，61(2)：429-438.

[7] SAHA M，GHOSH R，GOSWAMI B.Robustness and Sensitivity Metrics for Tuning the Extended Kalman Filter [J].IEEE Trans.Instrum.Meas.，2014，63(4)：964-971.[8] 魏喜庆，宋申民.基于改进容积卡尔曼滤波的奇异避免姿态估计[J].航空学报，2013，34(3)：610-619. WEI Xi-qing，SONG Shen-min.Improved Cubature Kalman filter Based Attitude Estimation Avoiding Singularity[J].Acta Aeronautica et Astronautica Sinica，2013，34(3)：610-619.

[9] KANDEPU R，FOSS B，IMSLAND L.Applying the Unscented Kalman Filter for Nonlinear State Estimation [J].J.Process Control，2008，18(7-8)：753-768.

[10] DINI D H，MANDIC D P，JULIER S J.A Widely Linear Complex Unscented Kalman Filter [J].IEEE Signal Process.Lett.，2011，18(11)：623-626.

[11] GUSTAFSSON F，HENDEBY G.Some Relations between Extended and Unscented Kalman Filters [J].IEEE Trans.Signal Process，2012，60(2)：545-555.

[12] 贾瑞才.重力/地磁辅助的欧拉角无迹卡尔曼滤波姿态估计[J].光学精密工程，2014，22(12)：3280-3286. JIA Rui-cai.Attitude Estimation Base on Gravity/ Magnetic Assisted Euler Angle UKF[J].Optics and Precision Engineering，2014，22(12)：3280-3286.

[13] 刘华，吴文，王世元.基于平方根CKF的多传感器序贯式融合跟踪算法[J].系统工程与电子技术，2015，37(7)：1494-1498. LIU Hua，WU Wen，WANG Shi-yuan.Multi-Sensor Sequential Fusion Tracking Algorithm Based on Square-Root Cubature Kalman Filter[J].Systems Engineering and Electronics，2015，37(7)：1494-1498.

[14] ARASARATNAM I，HAYKIN S.Cubature Kalman Filters [J].IEEE Trans.on Autoynatic Control，2009，54(6)：1254-1269.

[15] 胡振涛，曹志伟，李松，等.基于容积卡尔曼滤波的异质多传感器融合算法[J].光电子·激光，2014，25(4)：697-703. HU Zhen-tao，CAO Zhi-wei，LI Song，et al.Hererogeneous Multi-Sensor Fusion Algorithm Based on Cubature Kalman Filter[J].Journal of Optoelectronics·Laser，2014，25(4)：697-703.

[16] 钱华明，黄蔚，葛磊.基于改进的迭代容积卡尔曼滤波姿态估计[J].哈尔滨工业大学学报，2014，46(6)：116-122. QIAN Hua-ming，HUANG Wei，GE Lei.Attitude Estimation Based on Improved Iterated Cubature Kalman Filter [J].Journal of Harbin Institute of Technology，2014，46(6)：116-122.

[17] 康轶非，宋永端，宋宇，等.平方根容积卡尔曼滤波在移动机器人SLAM中的应用[J].机器人，2013，35(2)：186-193. KANG Yi-fei，SONG Yong-duan，SONG Yu，et al.Square-Root Cubature Kalman Filter and Its Application to SLAM of an Mobile Robot[J].Robot，2013，35(2)：186-193.

[18] 王松，田波，战榆莉，等.基于修正EKF的微小型飞行器姿态估计[J].高技术通讯，2011，21(6)：612-618.

WANG Song，TIAN Bo，ZHAN Yu-li，et al.Flight Attitude Estimation for MAVs Based on Amended EKF[J].Chinese High Technology Letters，2011，21(6)：612-618.

[19] 贾瑞才.基于四元数EKF的低成本MEMS姿态估计算法[J].传感技术学报，2014，27(1)：90-95. JIA Rui-cai.Attitude Estimation Algorithm for Low Cost MEMS Based on Quaternion EKF[J].Chinese Journal of Sensors and Actuators，2014，27(1)：90-95.

[20] JONGHEE B，YOUDAN K.Nonlinear Estimation for Spacecraft Attitude Using Decentralized Unscented Information Filter[C]∥International Conference on Control Automation and Systems.Korea：2010：1562-1566.

Cubature Attitude Estimation for Micro Aerial Vehicles Based on Multi-Sensor Fusion

SHI Zhang-song，WU Zhong-hong，LIU Jian，FU Bing

(Naval University of Engineering，College of Electronic and Engineering，Hubei Wuhan 430033，China)

For micro electromechanical system (MEMS), the gyroscope has the problem of low accuracy, high noise and time quickly accumulated error; while extended kalman filter (EKF) has the problem of linearization error; and unscented kalman filter (UKF) has the problem of high time cost. Therefore, a cubature attitude estimation method for micro aerial vehicle is proposed. An attitude kinematics model based on Euler angles is established. Taking attitude angle as the filter state and outputs of accelerometer and magnetometer as measurement, the cubature numerical integration theory is used to calculate the mean and variance of the nonlinear function. On this basis, cubature Kalman filter (CKF) attitude estimation for micro aerial vehicle with multi-sensor assisted is realized. Simulation results show that the estimation accuracy of CKF is equivalent to that of UKF and better than EKF; the stability of CKF is equivalent to UKF and better than EKF; and the time consumption of CKF is better than UKF.

nonlinear filtering; cubature Kalman filter；Euler angles；multi-sensor；attitude estimation；micro aerial vehicles

2016-03-15；

2016-08-10

有

石章松(1975-)，男，湖北黄石人。教授，博士，主要研究方向为信息融合，目标定位与跟踪。

通信地址：430033 湖北省武汉市解放大道717号147号信箱 E-mail：yizhousan@163.com

10.3969/j.issn.1009-086x.2017.03.006

TP273;TP212.9;TP391.9

A

1009-086X(2017)-03-0034-06