无叶扩压器中非定常流动的DMD模态分析
2017-06-26胡晨星刘鹏寅竺晓程杜朝辉
丁 杰, 胡晨星, 刘鹏寅, 竺晓程, 杜朝辉
(上海交通大学 机械与动力工程学院,工程热物理研究所,上海 200240)
无叶扩压器中非定常流动的DMD模态分析
丁 杰, 胡晨星, 刘鹏寅, 竺晓程, 杜朝辉
(上海交通大学 机械与动力工程学院,工程热物理研究所,上海 200240)
采用动力模态分解(DMD)对离心压气机无叶扩压器内的复杂流场进行分析,选取1.8 kg/s设计工况和1.4 kg/s非稳定工况下的非定常数值计算结果为基础数据,得到这2种工况下10%叶高平面上切向速度、径向速度的模态云图以及特征频率,评估了DMD方法分析离心压气机非定常流动特征的能力.对不同特征频率下的流场进行重构,直观深入地再现了无叶扩压器内部非定常流动的变化过程.结果表明:在小质量流量下,叶片扫描频率的影响效果虽然仍占据主导,但受到抑制;捕捉到失稳频率约为193 Hz,失稳模态在扩压器内沿周向占据3个固定的位置交替波动,不稳定波动沿扩压器周向并不存在旋转.
离心压气机; 无叶扩压器; 非定常流动; 动力模态分解
压气机的工作范围在大流量下受流道堵塞的限制,在小流量下则受到失速和喘振[1]等非稳定流动的限制.一旦旋转失速出现,叶片所承受的长时间振动应力将导致压气机转子叶片寿命降低.而发生喘振时,叶片和机匣都承受很大的瞬时力作用,会导致严重的破坏[2].因此,失速和喘振一直是阻碍压气机优化设计的重要因素,有必要对其产生和发展过程的流动机制进行全面深入的研究[3-5].
相关专家学者已经对离心压气机内的失速和喘振现象展开了大量的实验研究,Frigne等[6]实验研究了带无叶扩压器的离心压气机内扩压器和离心叶轮的失速流动.Lawless[7]提出了失速先兆的检测和判断方法,通过实验分析了离心压气机内部旋转失速和喘振的初始状态特征.Hunziker等[8]观察到了离心压气机的诱导失速、轻度失速、深度失速以及不同有叶扩压器下的失速流动.
近年来,数值模拟技术开始应用到离心压气机失稳现象的研究上,并取得了一定成果.常用数值计算方法是给定出口的背压或流量[9-12]来获得不同流量下的流动数据.而通过提高背压来获得小流量下的流场会存在计算发散的问题,一般采用节流阀模型来解决该问题[13].Guo等[14-15]假定在蜗壳后存在气腔和节流阀,推导得到出口条件表达形式,再对不同流量下的流场进行了详细的分析.Zhu等[16]采用几何节流阀技术对离心压气机进行整体的三维N-S计算,获得了从堵塞到失速工况的流动特征.刘海清等[17]比较了设计点与近失速点下无叶扩压器内部的流动特征.
动力模态分解(DMD)是一种近年来应用较为广泛的模态分解方法,适用于从复杂流场中分解出大尺度的流动结构.Schmid等[18-19]给出了DMD的详细理论推导.Seena等[20]通过DMD分析了紊乱腔流中的自持振荡.Dunne等[21]采用DMD方法分析了一个低阶的动态失速模型,获得了动态失速分离的主要模态.Liu等[22]采用DMD处理了有限钝板周围的流动分离,直观地分析了分离流动的非定常特征.
笔者基于离心压气机的非定常数值计算结果,采用DMD对离心压气机无叶扩压器内的复杂流场进行分析,选取1.8 kg/s设计工况和1.4 kg/s非稳定工况下的非定常数值计算结果为基础数据,得到这2种工况下10%叶高平面上切向速度、径向速度的模态云图以及特征频率,评估DMD方法在分析离心压气机非定常流动特征的能力.同时,对不同特征频率下的流场进行重构,直观深入地再现了无叶扩压器内部非定常流动的变化过程.
1 数值模拟
研究对象为离心压气机模型GT70.该模型由离心叶轮(包括进口管道)、无叶扩压器、蜗壳以及排气管组成.叶轮叶片分为6个大叶片和6个小叶片.进口边界给定总温总压,出口边界给定静压,壁面为绝热无滑移边界.流动模型选取SSTk-ω模型.时间步长为1.131×10-5s,即一个大叶片流道设置20个时间步长.详细的设定参数和计算步骤见文献[16].
图1给出了离心压气机不同质量流量下总压比的CFD数值计算结果与实验测量结果,图中纵坐标总压比为收缩管中间位置的总压与压气机进口总压的比值,其中1.8 kg/s为设计质量流量.由图1可知,随着质量流量的增大,总压比逐渐下降达到了堵塞状态;而随着质量流量的减小,性能曲线在质量流量1.49 kg/s后开始下降,总压比曲线斜率为正,可以认为流动出现失速.从图1还可以看出,数值计算得到的总压比值均略大于实验测量结果,总体上可认为数值计算结果与实验测量结果近似吻合.且图1还给出了小质量流量下压力和流量的波动范围,定量反映了压气机在小质量流量下的性能波动特征.

图1 数值计算结果与实验测量结果的对比
在进行非定常计算时,对部件内的流动进行压力或流量的监控,通过频谱分析获得非定常流动的特征频率.图2为无叶扩压器和排气管内布置的2个监控点P1和P2的位置示意图.

图2 监控点位置示意图
图3给出了质量流量为1.4 kg/s和1.8 kg/s时,无叶扩压器内监控点P1处压力波动的频谱分析结果.由于在计算过程中叶轮转速为44 198 r/min,则叶轮旋转频率为736.6 Hz.叶片数为12,故叶片通过频率(Blade Passing Frequency, BPF)为8 839.6 Hz,大叶片通过频率为4 419.8 Hz.
当质量流量为1.8 kg/s时,叶片通过频率的幅值非常明显,除此之外监控点再没有出现其他明显的离散频率,说明此时的流动还处于比较稳定的状态.而质量流量为1.4 kg/s时,监控点出现了一个离散的频率229.84 Hz.该频率值接近叶轮旋转频率的三分之一,根据Hoying等[23]的说法,模态失速频率大约是叶轮旋转频率的1/4~1/2,可认为229.84 Hz是失速频率.

(a) 设计工况1.8 kg/s
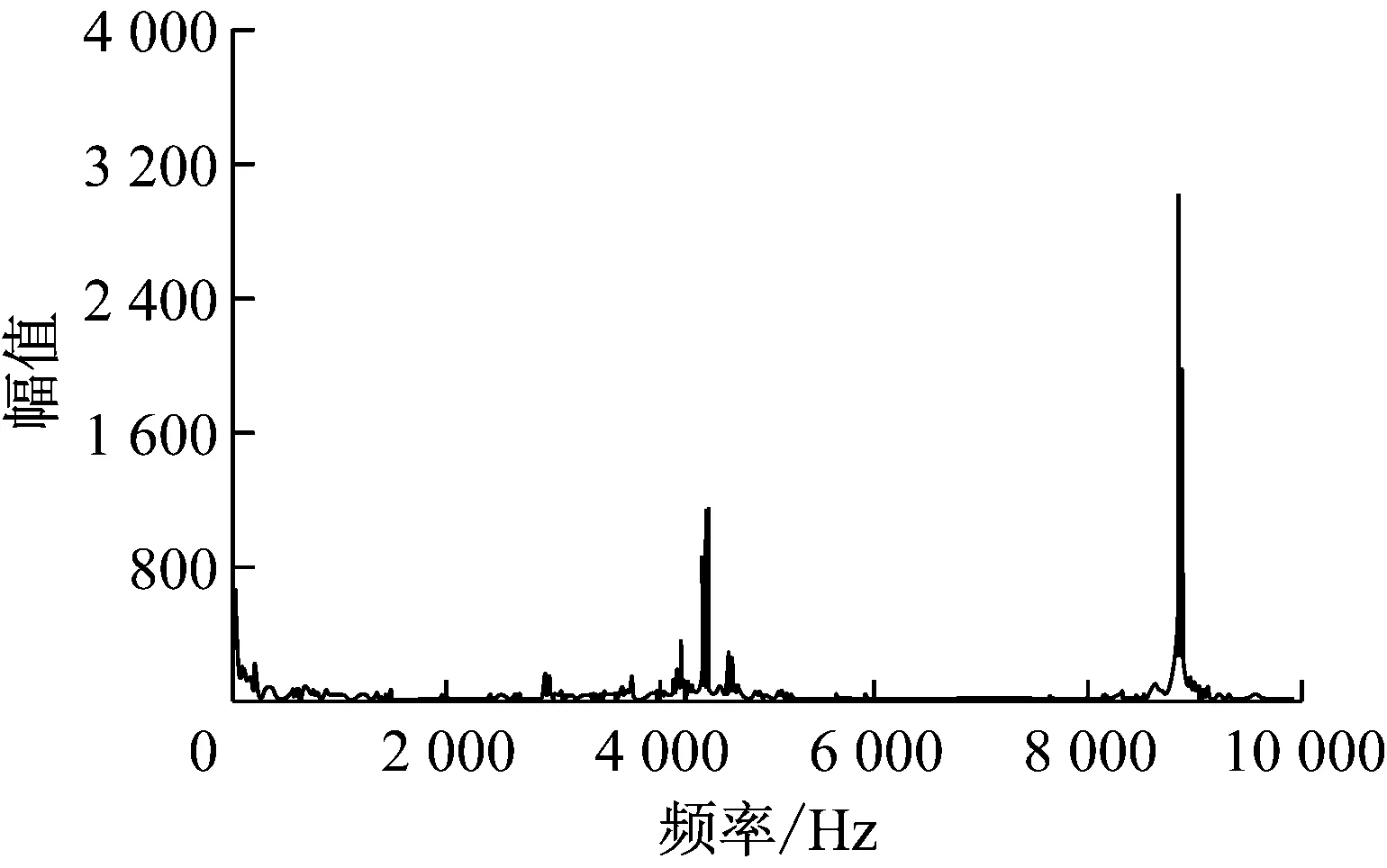
(b) 非稳定工况1.4 kg/s
2 动力模态分解
下面针对DMD方法最常用的Arnoldi算法进行简单介绍[18-19].
假定有一组随时间变化的数据矩阵:
(1)
式中:N为时间步总数;vi为第i时间步的数据组成的向量.
假定vi+1和vi之间存在一个线性的映射关系A:
vi+1=Avi
(2)
可以将原数据矩阵改写成:
(3)
若将最后一个时间步的数据用前几个时间步的数据进行线性组合,则:
(4)
将其写成矩阵形式如下:
(5)
式中:aT=[a1a2…aN];r为残差向量.
按式(5)可以得到如下关系式:
(6)
其中矩阵S为如下形式:
(7)
如果不存在残差向量r,则矩阵S的特征值将是矩阵A的特征值的一个子集.如果残差向量r不为零向量,则矩阵S的特征值是矩阵A的特征值的近似.由于该矩阵是病态矩阵,在求解特征值时存在困难,因此一般进行以下转换.
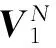
(8)
将式(6)代入式(8)中可以得到:
(9)


(10)
最终得到DMD模态如下:
Φi=Uyi
(11)
需要指出的是,各阶DMD模态的范数表明了该模态的能量大小,而其相应的特征值就包含了该模态的频率和增长率信息.

λi=ln(μi)/Δt
(12)
特征值的实部Re(λi)是DMD模态Φi的时间增长率,而特征值的虚部Im(λi)/2π是模态Φi的频率,式中Δt是每个流场快照之间的时间步长.
3 结果与分析
在非定常计算中,作为DMD处理时的Δt设定为5个时间步长,即5.655×10-5s.一共选取了600个时间步长的原始流场数据,即120个原始流场快照,故DMD分解的最低分辨频率大约为29 Hz.而频谱分析选取了5 000个时间步长的数据进行处理,最低分辨频率大约为17 Hz.
3.1 设计工况
图4给出了1.8 kg/s质量流量下10%叶高平面非定常流场的DMD模态特征值.图中以特征值实部为横轴,虚部为纵轴,几乎所有的主要特征值都分布在单位圆上.
图5给出了DMD各阶模态对应频率及能量比(取对数后)的关系.从图5可以看到能量比最高的前四阶模态,其中第二、第三阶模态的频率为图3(a)频谱分析得到的叶片扫描频率,可见DMD对于特征频率具有良好的捕捉能力.
图6给出了设计工况下前四阶模态的切向速度和径向速度云图,本文所有云图(模态和重构)均经过归一化处理.从图6可以看出,第一阶零频模态是平均流场,展现了原流场中占主导地位的流动结构.蜗舌的存在,影响了周向周期性的速度分布.无叶扩压器切向流动基于角动量守恒,随着半径的增大,切向速度逐渐减小.第三阶模态中在周向分别有12个周期变化的速度分布,对应12个叶轮叶片;第二阶模态中在周向分别有了6个周期变化的速度分布,对应6个叶轮大叶片.这表明DMD捕捉到了上游叶轮叶片通过所造成的射流-尾流结构的影响.

图4 设计工况下特征值的分布图
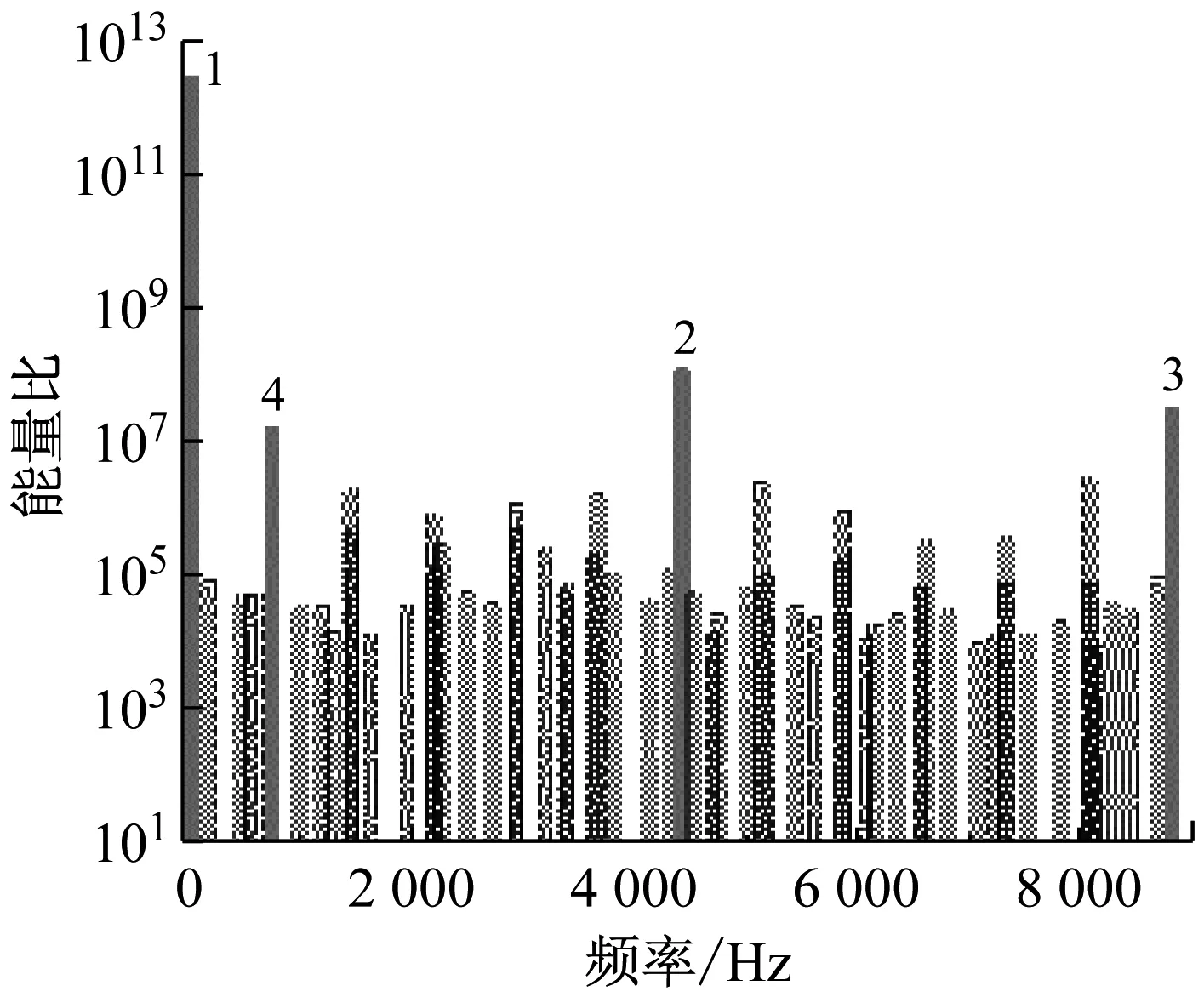
图5 设计工况下能量比的分布图

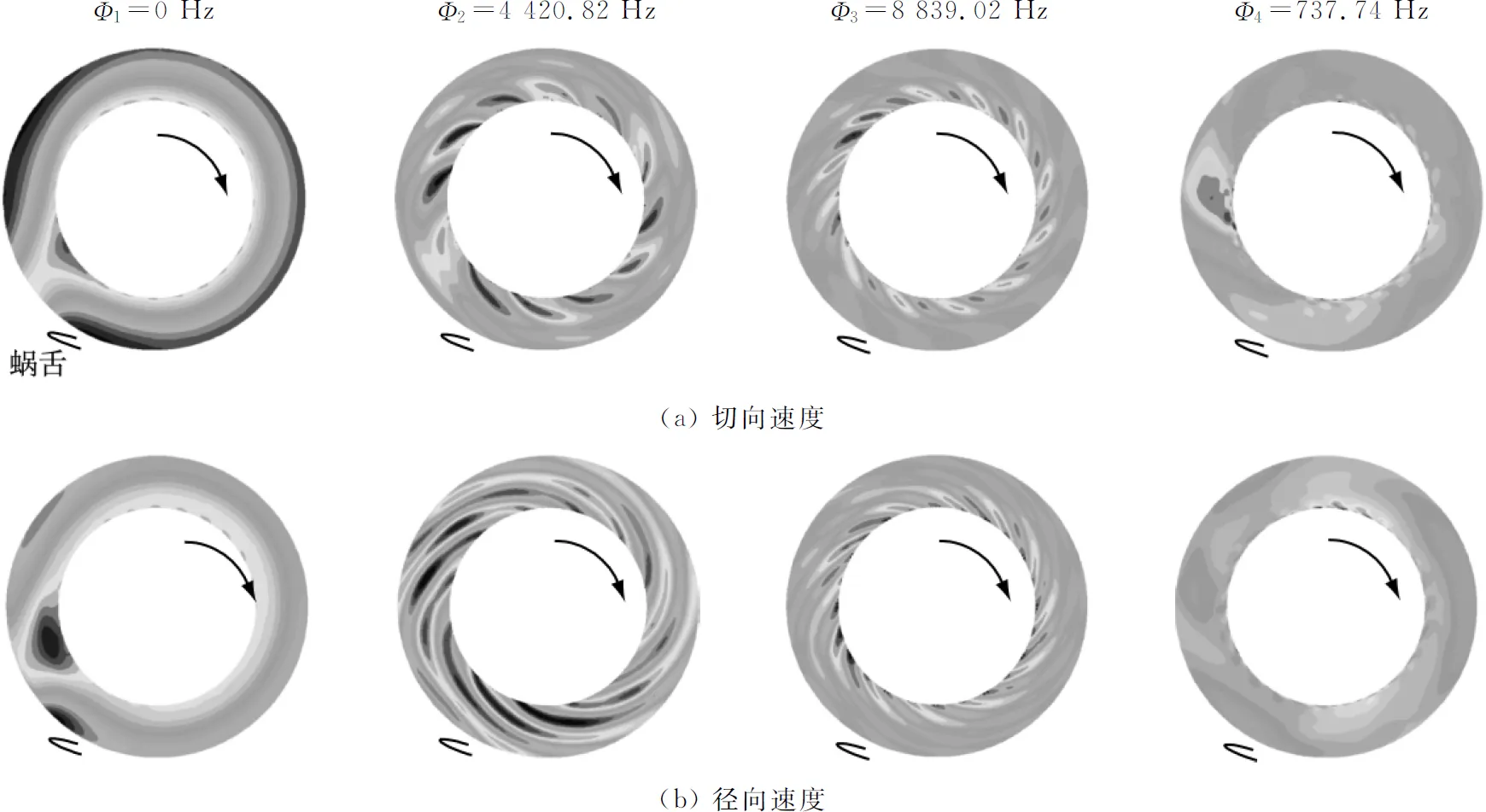
图6 设计工况下前四阶模态切向速度和径向速度云图
3.2 非稳定工况
图7给出了1.4 kg/s质量流量下10%叶高平面DMD模态的特征值.由图7可知,几乎所有的特征值均分布在单位圆上.
图8给出了各阶模态对应频率及其能量比(取对数后)的关系.从图8可以看出,除叶片扫描频率外,第四阶模态还捕捉到了低频率的流动不稳定频率.
图9给出了非稳定工况下前四阶模态的云图及其对应的频率值.由图9可知,由于DMD和频谱分析的最低分辨频率分别约为29 Hz和17 Hz.第四阶模态所获得的频率值为失速频率.
图9中第一阶零频模态仍是平均流场,与设计工况的对应模态类似,但周向不均匀性加剧;第二阶叶片通过频率对应的模态和第三阶大叶片通过频率对应的模态中,由于内部非稳定流动的影响,叶轮的射流-尾流结构影响明显弱化;第四阶失速频率对应的切向速度和径向速度流动模态中,周向存在多个流动失稳区,将通过重构来直观地观察该流动区域的非定常变化.

图7 非稳定工况下特征值的分布图
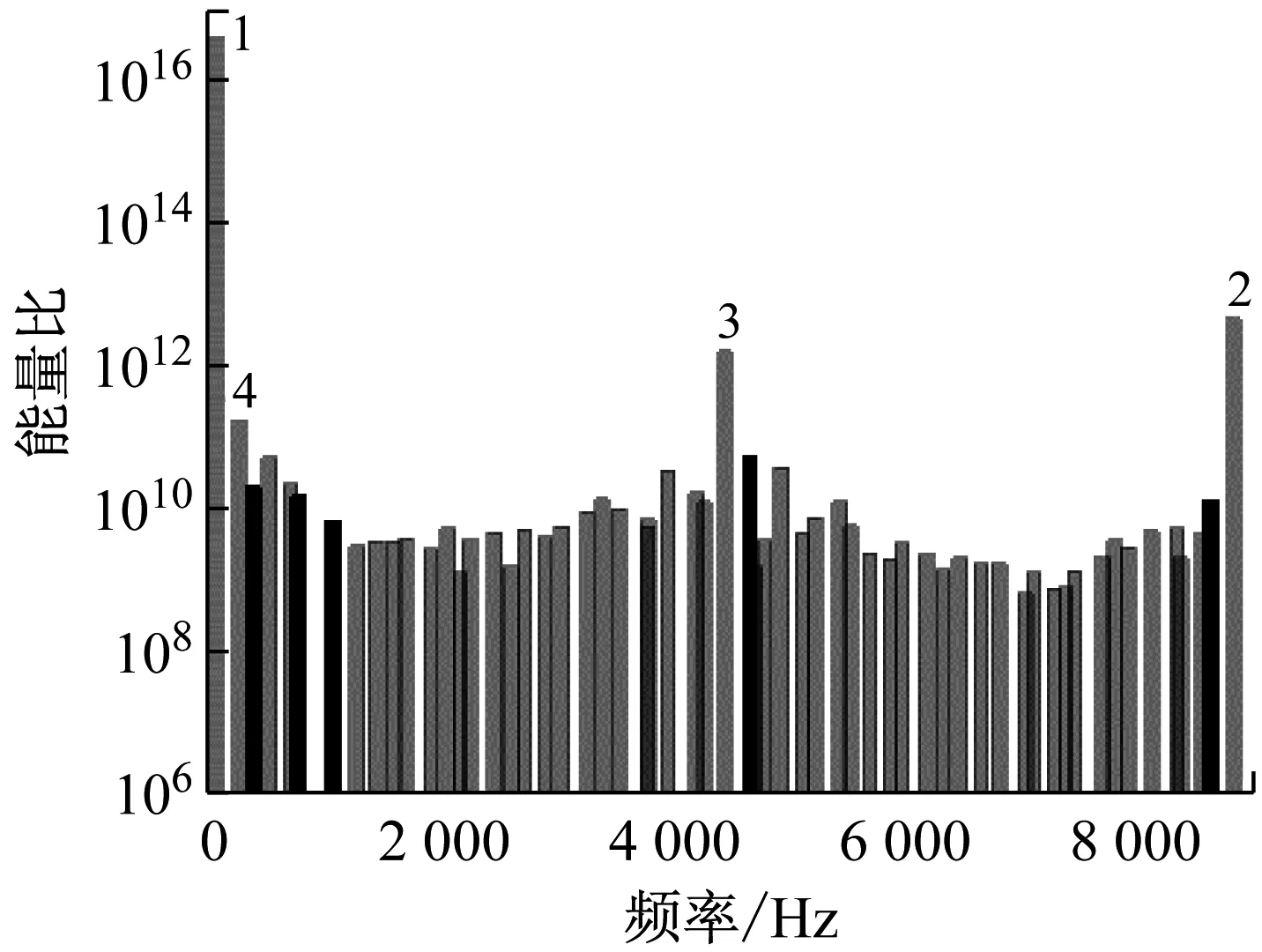
图8 非稳定工况下能量比的分布图

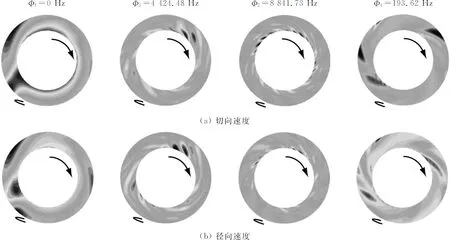
图9 非稳定工况下前四阶模态切向速度和径向速度云图
3.3 流场重构
为了研究无叶扩压器内部特定的流动结构,采用模态重构的方法得到该模态随时间变化的过程,直观地给出流动特征.
图10给出了非稳定工况下某个时刻径向速度原始流场与前四阶频率对应模态的重构云图.由图10可知,相似的流场分布说明DMD得到的前四阶模态基本包含了原始流场的流动信息.
图11给出了设计工况下一个叶片扫描周期内不同时刻径向速度在叶片通过频率对应模态(第二阶模态)的重构云图,由于采用频率的限制,对应周期内只能重构2个时刻流场.前后不同时刻下射流-尾流结构始终占据主导地位,该结构周向转过1/2流道,对应叶轮的旋转扫描过程.
图12给出了非稳定工况下第四阶失速频率对应周期内不同时刻下,径向速度在叶片通过频率对应模态的重构云图.从图12可以看出,周向存在3个明显的非稳定流动区域,一个周期内经历正负径向速度一次交替变化过程.通过模态重构,直观地给出了失稳流动的作用范围,发现在绝对坐标下失稳流动是不旋转的.

4 结 论
(1)采用CFD数值模拟的方法得到了离心压气机GT70在不同质量流量下的非定常流场数据,计算得到的离心压气机性能曲线与实验测量结果基本吻合.
(2)通过DMD方法对设计工况下的非定常流场进行分析,证明在设计工况下,扩压器内流场主要受到叶片扫描频率的影响,并且呈现射流-尾流的交替结构.
(3)通过DMD方法对小质量流量下的非定常流场进行分析,发现在失稳工况下,叶片扫描频率的影响效果虽然仍然占据主导,但受到抑制.同时,捕捉到失稳频率约为193 Hz,失稳模态呈现为在扩压器内沿周向占据3个固定的位置交替波动.
(4)将前四阶频率多模态重构、叶片扫描频率和失速频率单模态重构,证明了失稳模态沿扩压器周向并不存在旋转,而是以类似驻波的形式发展,并且其中一个失速团与蜗舌的位置相同.
DMD方法结合CFD非定常计算有助于直观深入地认识离心压气机失稳工况的非定常流动问题,有助于对其流动机理的理解.
[1] EMMONS H W, PEARSON C E, GRANT H P. Compressor surge and stall propagation[J]. Transactions of ASME, 1955, 77(3): 455-469.
[2] 唐狄毅. 叶轮机非定常流[M]. 北京: 国防工业出版社, 1992.
[3] EVERITT J N, SPAKOVSZKY Z S. An investigation of stall inception in centrifugal compressor vaneddiffuser[J]. Journal of Turbomachinery, 2013, 135(1): 011025.
[4] JYOTHISHKUMAR V, MIHAESCU M, SEMLITSCH B, et al. Numerical flow analysis in centrifugal compressor near surge condition[C]//43rd Fluid Dynamics and Co-Located Conferences. San Diego, USA: AIAA,2013: 13.
[5] VAGANI M, ENGEDA A, CAVE M J. Prediction of impeller rotating stall onset using numerical simulations of a centrifugal compressor. Part 2: evaluation of mass-flow fluctuations at rotor-stator interfaces[J]. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2013, 227(4): 415-425.
[6] FRIGNE P, van DEN BRAEMBUSSCHE R. Distinction between different types of impeller and diffuser rotating stall in a centrifugal compressor with vaneless diffuser[J]. Journal of Engineering for Gas Turbines and Power, 1984, 106(2): 468-474.
[7] LAWLESS P B. Experimental evaluation of precursors to centrifugal compressor instability[J]. International Journal of Turbo and Jet Engines, 2000, 17(4): 279-288.
[8] HUNZIKER R, GYARMATHY G. The operational stability of a centrifugal compressor and its dependence on the characteristics of the subcomponents[J]. Journal of Turbomachinery, 1994, 116(2): 250-259.
[9] XI G, MA Y, WU G K, et al. Exploration of a new-type grooved casing treatment configuration for a high-speed small-size centrifugal compressor[J]. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2013, 227(4): 464-478.
[10] DICKMANN H P, WIMMEL T S, SZWEDOWICZ J, et al. Unsteady flow in a turbocharger centrifugal compressor: three-dimensional computational fluid dynamics simulation and numerical and experimental analysis of impeller blade vibration[J]. Journal of Turbomachinery, 2006, 128(3): 455-465.
[11] WANG Tong, WANG Wei, GU Chuangang. Unsteady simulation and analysis on centrifugal impeller with self-adaptive casing treatment[C]//ASME Turbo Expo 2013: Turbine Technical Conference and Exposition. San Antonio, Texas, USA:ASME, 2013.
[12] 杨晓清. 基于CFD的轴流式压缩机与风机性能及改进设计研究[D].大连:大连理工大学, 2013.
[13] HE L. Computational study of rotating-stall inception in axial compressors[J]. Journal of Propulsion and Power, 1997, 13(1): 31-38.
[14] GUO S, CHEN Hua, ZHU Xiaocheng, et al. Numerical simulation of surge in turbocharger centrifugal compressor: influences of downstream plenum[C]//ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition. Vancouver, British Columbia, Canada:ASME, 2011: 1897-1908.
[15] 郭强. 带无叶扩压器的离心压缩机失速现象的实验和数值研究[D].上海:上海交通大学, 2007.
[16] ZHU Xiaocheng, JIA Kai, DU Zhaohui. Prediction of centrifugal compressor performance from choke through stall with a physical throttle[C]//ASME Turbo Expo 2015: Turbine Technical Conference and Exposition. Montreal, Quebec, Canada:ASME, 2015.
[17] 刘海清, 高闯, 张宏武, 等. 带无叶扩压器离心压气机的稳定性分析[J].动力工程学报, 2013, 33(12): 936-941.
LIU Haiqing, GAO Chuang, ZHANG Hongwu, et al. Stability analysis of centrifugal compressor with vaneless diffuser[J].Journal of Chinese Society of Power Engineering, 2013, 33(12): 936-941.
[18] SCHMID P J. Dynamic mode decomposition of numerical and experimental data[J]. Journal of Fluid Mechanics, 2010, 656: 5-28.
[19] SCHMID P J, LI L, JUNIPER M P, et al. Applications of the dynamic mode decomposition[J]. Theoretical and Computational Fluid Dynamics, 2011, 25(1): 249-259.
[20] SEENA A, SUNG H J. Dynamic mode decomposition of turbulent cavity flows for self-sustained oscillations[J]. International Journal of Heat and Fluid Flow, 2011, 32(6): 1098-1110.
[21] DUNNE R, MCKEON B J. Dynamic stall on a pitching and surging airfoil[J]. Experiments in Fluids, 2015, 56: 157.
[22] LIU Yingzheng, ZHANG Qingshan. Dynamic mode decomposition of separated flow over a finite blunt plate: time-resolved particle image velocimetry measurements[J]. Experiments in Fluids, 2015, 56: 148.
[23] HOYING D A, TAN C S, VO H D, et al. Role of blade passage flow structurs in axial compressor rotating stall inception[J]. Journal of Turbomachinery, 1999, 121(4): 735-742.
Dynamic Mode Decomposition of the Unsteady Flow in a Vaneless Diffuser
DING Jie, HU Chenxing, LIU Pengyin, ZHU Xiaocheng, DU Zhaohui
(Institute of Engineering Thermophysics, School of Mechanical Engineering, Shanghai Jiaotong University, Shanghai 200240, China)
Taking the simulation results under design condition 1.8 kg/s and unsteady condition 1.4 kg/s as the basic data, an analysis was conducted on the complex flow field in the vaneless diffuser of a centrifugal compressor using dynamic mode decomposition (DMD), so as to obtain the contours of tangential and radial velocity modes at 10% span plane as well as the characteristic frequencies, and to evaluate the applicability of DMD method in analyzing the unsteady flow within the vaneless diffuser. In addition, flow field reconstruction was conducted at different characteristic frequencies to figure out the transformation of unsteady flow in the diffuser. Results show that at small mass flow rates, the predominant effect of blade passing frequency is suppressed; the eigen mode corresponding to stall does not rotate along the circumferential direction, where three stall cells can be observed, and the frequency of stall is about 193 Hz.
centrifugal compressor; vaneless diffuser; unsteady flow; dynamic mode decomposition
2016-08-10
2016-09-18
丁 杰(1991-),男,浙江海盐人,硕士研究生,主要从事叶轮机械方面的研究.电话(Tel.):15801859823; E-mail:onze_vov@sjtu.edu.cn.
1674-7607(2017)06-0447-07
TK472
A
470.30
