木节对轴心受压胶合木柱稳定承载力的影响
2017-06-26郭宇航周淑容崔佳黄宗明
郭宇航+周淑容+崔佳+黄宗明

摘要:采用压杆挠曲线法分析了木节对轴心受压胶合木柱稳定承载力的影响,分析时考虑了初弯曲、初偏心以及木节和木材本构的弹塑性等因素的影响。在考虑木节的影响时,模型中将截面分为木节区、木节影响区和无影响区,3个区域分别采用不同的本构模型,木节区的位置由自编程序随机产生,以模拟实际工程中木节在构件中的随机分布。分别计算了木节率为2%、6%和9%时的稳定系数φ。计算结果表明,木节会在一定程度上降低轴心受压胶合木柱的稳定承载力。数值计算结果和试验数据的对比表明,数值计算结果与试验结果吻合较好。
关键词:胶合木柱;压杆挠曲线法;稳定性;木节影响
中图分类号:TU366.3文献标志码:A文章编号:16744764(2017)03004406
Abstract:The effect of knot was analyzed on stability of glulam column under Axial Compressive Loading, using the column deflection curve method (CDC method). The initial bending, eccentricity, wood knots and elasticplasticity of wood were considered for analysis. The member in the model was divided into three areas: knot area, knot influence area and no influence area, and three related constitutive relations were adopted in the process of analyzing. The locations of knots were randomly generated by designed program to simulate the randomly distributed knots in practical components. The stability coefficient φ was calculated considering knot at the rate of 2%, 6% and 9%, respectively. The results showed that the knots could reduce the stability capacity of the glulam column in axial compression in some degree. The numerical data was further compared with the test data and they were fit well each other.
Keywords:glulam column; column deflection curve method; stability; effect of knot
关于轴心受压胶合木柱的稳定承载力计算方法,通常采用切线模量理论推导出理论计算公式,再通过大量不同长细比、不同强度等级木材的稳定承载力试验,用试验数据拟合公式中的参数获得。《胶合木结构技术规范》(GB/T 50708—2012) [1]中轴心受压构件的稳定计算公式,参照美国木结构设计规范[2]转化而来。美国木结构设计规范采用的是Ylinen公式[35],其参数c由试验数据拟合得到,体现了木材的初始缺陷的影响。加拿大木结构设计规范[6]采用的CRG(Cubic RankineGordon)公式[78]中的形状系数N也是由试验数据拟合得到的。事实上,轴心受压胶合木柱的实际失稳形式属于极值点失稳,运用最大强度理论计算轴心受压胶合木柱的稳定承载力比运用切线模量理论更符合构件失稳的实际状态。由于木材种类繁多,胶合木的组坯方式也较多,材料的力学性能变异性较大。因此,要得到不同强度等级、不同长细比的轴压构件的稳定承载力,通常需要做大量试验,成本较高。基于上述两点原因,运用最大强度理论,借助数值方法计算轴心受压胶合木柱的稳定承载力具有重要意义。压杆挠曲线法(简称CDC法)是一种常用的数值方法,在钢结构领域有广泛应用,已被用来分析计算各种钢结构截面形式和受力条件下的稳定问题[911]。初始缺陷是影响轴心受压构件稳定承载力的重要因素,轴心受压胶合木柱的初始缺陷包括初偏心、初弯曲和木材的天然缺陷等。其中,木材的天然缺陷很多,除木节外还包括斜纹、裂纹、腐朽和虫蛀等。研究表明,木节是影响木材均质性和力学性能的重要缺陷,相比之下其他材料缺陷的影响要小得多。已有不少关于木节对木材力学性能影响的研究,包括木节对抗弯性能、抗拉性能的影响[1215]等,但没有关于木节对轴心受压木构件稳定承载力影响的研究。笔者采用CDC法,在考虑初偏心和初弯曲的情况下,分析木节对轴心受壓胶合木柱稳定承载力的影响。
1压杆挠曲线法
对于两端铰接的轴心受压杆件,当不考虑杆件的材料缺陷(弹塑性和木节等)和几何缺陷(初偏心和初弯曲)时,杆件失稳时的挠曲线是一条正弦半波曲线。当计入几何缺陷后,挠曲线虽然可能不是一条标准的正弦半波曲线,但仍可以通过直接积分得到挠曲线的解析表达式。如果还要同时考虑材料缺陷,要得到挠曲线的解析表达式已经不可能了。Chen[16]提出可用数值积分的方法计算,其基本思想是将杆件划分为若干个单元段,假定每一段的变形曲线是一条圆弧,然后建立递推关系。根据初始条件即可求得各分段点的挠度、转角和曲率,这样就可以得到杆件的挠曲线。通过挠曲线可以进一步计算得到杆件的稳定承载力Pu。
1.1稳定承载力Pu的计算
轴心受压构件失稳时的挠曲线是连续曲线,因此,CDC法建立的挠曲线y(z)是连续的,它的一阶导数转角θ(z)也是连续的,而二阶导数曲率Φ(z)是分段的。图1所示为两端铰接轴心受压杆件,将杆件划分为n段,每段长度为a,以每一个单元段左端的曲率Φi代表该单元段的曲率,其值为常数。这样就可以通过几何关系建立挠度yi、转角θi和曲率Φi之间的递推关系式θi =θi-1-aΦi-1(1)
yi=yi-1+aθi-1 -a2Φi-1/2(2)
Mi=P(yi+e0+v)(3)
Φi=f(Mi,P)(4)式(3)中:e0为初偏心;v为初弯曲,可近似假定为最大初始挠度为v0的正弦曲线v=v0sin(πz/l)=v0sin(πi/n)。式(4)需要调用的MPΦ关系,将在后文叙述。
对于给定杆长为l的两端铰接杆件,支座节点的初始挠度y0=0,初始曲率Φ0=f(M0,P),M0=Pe0,不计初偏心时为0。计算时,先假定压力P和初始转角θ0,通过式(1)~(4)的递推关系可以求得任一分段截面的挠度yi、转角θi和曲率Φi。若杆件关于中点对称,则中点转角θm=0,中点挠度ym为最大挠度值。但如果考虑了木节(木节为程序随机生成得到),杆件将不再关于中点对称,所以,不能只计算到中点截面,要计算全长。直到杆件最右端挠度yn=0,如果yn不为0,需要改变初始转角θ0的值,直到yn=0。
如果假定的压力P小于稳定承载力Pu,那么总可以找到合适的初始转角θ0,使得yn=0。这样便可以得到一条完整的挠曲线,如图2(a)所示。如果假定的压力P大于稳定承载力Pu,计算过程中要么yn<0,要么出现截面破坏,找不到合适的初始转角θ0,使得yn=0,也就得不到一条完整的挠曲线,如图2(b)所示。利用这一点,运用二分法可以计算出稳定承载力Pu,即杆长为l的杆件所对应的稳定承载力。
1.2MPΦ关系的建立
将截面划分为若干个微小的单元,每个单元的面积为Ai,距弯曲轴的距离为xi,如图3所示。
要得到弯矩M、轴力P和曲率Φ三者的关系,可以先给定轴力P和曲率Φ,而后得到相应的弯矩M。这时需要假定初始值ε0,通过式(5)~(7)计算得到F。不断修正ε0,使得F=P。再通过式(8)计算得到弯矩M,计算结果如图4所示。图4给出了不同压力等级作用下弯矩M与曲率Φ的关系曲线(其中Pc=fcA,为杆件轴心受压强度破坏承载力)。为了方便对比,图4同时给出了考虑木节和不考虑木节时的弯矩–曲率关系。由图4可以看出,在同样的压力作用下,木节的存在降低了截面的抗弯承载力。当Φ=0时,有木节的截面弯矩不为0。说明木节造成了截面的偏心,从而产生了附加弯矩。
2木节的影响
在木材的天然缺陷中,木节对木材性能的影响最大。清材小试件的顺纹抗拉强度大于顺纹抗压强度,而足尺试件的顺纹抗拉强度小于顺纹抗压强度。这是因为木节对顺纹抗拉强度的影响最大,对顺纹抗压强度影响最小[17]。在木材受拉且拉力较小时,木节与周围木材断裂而退出工作。而在木材受压时,木节与周围木材一起承担压力。因此,在模拟计算时,木节区域可考虑为只压单元(即受压时强度不折减,而受拉时应力为0)。
木节对木材力学性能的影响不仅取决于木节的大小和位置(位于受拉区还是受压区),还受由木节引起的径切面斜纹的影响。甚至在某些情况下,由木节引起的径切面斜纹较木节直径的影响更大[15]。如图5所示,木节的存在使胶合木弦切板产生涡纹。但由于板面较宽,木节周围弯曲的纤维基本是连续的。而在其剖面(径切面)上,由于板材厚度较小,木材纤维被切断。所以,径切面斜纹对强度和刚度的影响较弦切面涡纹大。
1考虑木节和斜纹的影响,在计算模拟时采用如图6所示的模型。模型分为3个区域:木节区、木节影响区和无影响区。对于木节区,如前所述,采用只压模型;对于木节影响区,采用强度和刚度折减的办法,分别对顺纹抗拉强度、顺纹抗压强度和弹性模量进行折减。《胶合木结构技术规范》(GB/T 50708—2012)分别采用(或(9)和(10))Hankinson公式计算木材的斜纹抗压强度和斜纹抗拉强度
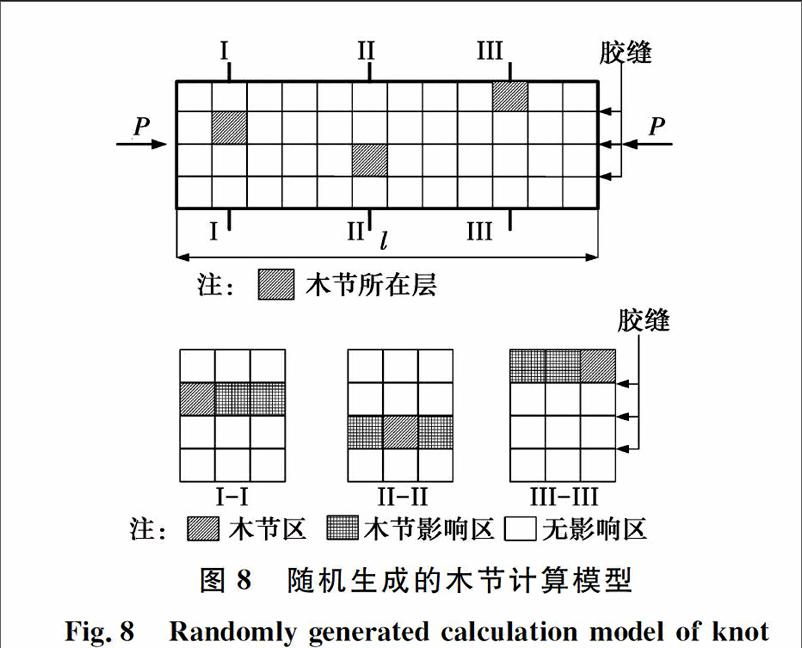
木节的尺寸一旦确定,影响构件稳定承载力的就是木节的位置和木节的数量。笔者在模拟木节时,木节的位置在程序中随机产生,而木节的数量通过木节生成的概率(木节率)来控制。图8为生成的某一有代表性的计算模型。其中,按前期试验统计,木节尺寸多数在20~30 mm范围内,相当于文献[1]中胶合木层板Ⅱd等材的材质等级规定的最不利木节尺寸限值,因此,模拟时木节宽度按文献[1]的限值取为板面宽度的1/3,木节率取为2%。
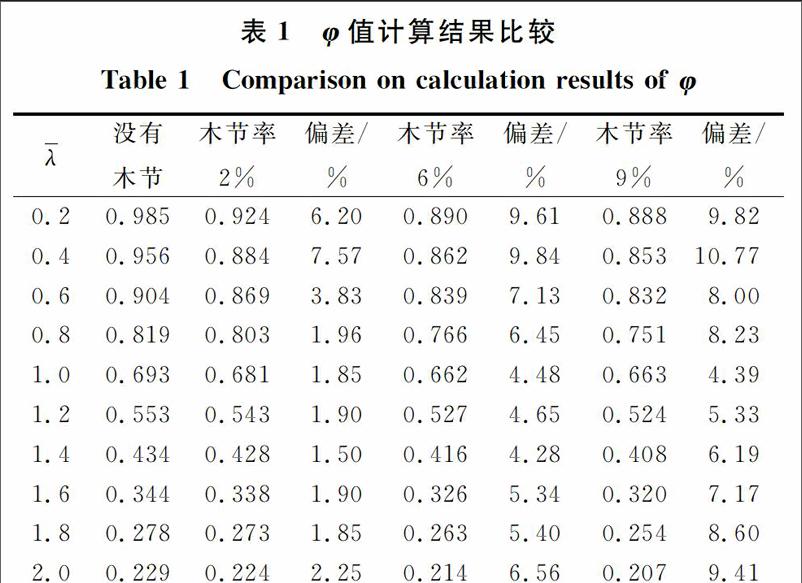
用此模型进行计算,随机生成木节,木节率分别取为2%、6%和9%,大致相当于《胶合木结构技术规范》的目测分级层板材质等级标准的Ⅰd、Ⅱd和Ⅲd的材质等级。将每种木节率所计算的稳定系数φ(稳定承载力与木材顺纹抗压强度的比值)与没有木节的计算结果进行比较,见表1。为了方便比较,表中采用相对长细比λ =λ/π(fc/E),各种木节率下的柱子曲线(稳定系数与长细比的关系曲线)如图9所示。
从表1和图9可以看出,对于每种木节率下的稳定系数φ的偏差,随相对长细比的变化趋势是先减小后增大,且在相对长细比λ=1附近最小。在相对长细比λ=2附近时,考虑木节与不考虑木节的稳定系数φ的偏差与木节率大致相等。
3试验验证
试件采用同等组合的胶合木,强度等级为TCT24,由4层北美进口花旗松目测分级规格材层板加工而成。试件按设计长细比50、70、90、110分为4组,分别对应A、B、C、D组。具体试验方法和加载装置等见文献[18]。4组试件的设计参数见表2。试验加载图见图10。
初始偏心e0根据每个试件在循环加载阶段的应变片的数据计算得到。分别计算每个试件的e0绝对值,算得平均值为l/2 500,该值包含了试件初弯曲和荷载初偏心的共同影响。因初弯曲和荷载初偏心都很小,将该值作为等效初偏心来考虑。
A、B、C、D 4组试件中,较为显著的缺陷是直径为20~30 mm的木节。在用CDC法计算时,分段的长度和单元的尺寸也在此范围内。针对这类较大的缺陷,对4组试件进行统计,得出每组试件出现木节的平均概率,将其作為每组试件的木节率代入模型进行计算。
将每种长细比杆件计算30次,然后取平均值。将每种长细比下稳定系数的数值计算结果的平均值与试验结果的平均值进行比较(见表3)。从表3可以看出,用CDC法计算的稳定系数φ与试验得到的稳定系数φ很接近。其中B、C、D组差值很小,在2%左右,A组相对较大,但都没超过8%。由于木材的力学性能变异性较大,试验获得的各组试件的稳定承载力的变异系数在7%~11%,因此,8%以内的偏差算合理的范围。
4结论
用CDC法对轴心受压胶合木柱的稳定承载力进行了数值分析,计算了木节率分别为2%、6%和9%的稳定系数φ,并将数值计算结果和试验结果进行了对比,得出以下结论:
1)在木材的初始缺陷中,木节是影响胶合木稳定承载力的重要因素。在长细比较大时,考虑木节与不考虑木节的稳定系数φ的偏差与木节率大致相等。对于短柱和长柱,木节对稳定承载力的影响相对较大;对于中等长度的柱,木节对稳定承载力的影响较小。
2)稳定系数的数值计算结果与试验结果很接近,说明CDC法的计算模拟效果较好,计算数据较可靠。因此,后期可用此模型分析其他强度等级、其他截面形式轴心受压胶合木柱的稳定承载力,还可以用于压弯构件稳定承载力的计算。
3)CDC法作为稳定计算的重要方法,已在钢结构领域有着广泛应用。通过分析可以看出,将其运用于木结构也是一种计算精度较高的方法。
参考文献:
[1] 胶合木结构技术规范: GB/T 50708—2012 [S]. 北京:中国建筑工业出版社,2012.
Technical code of glued laminate timber structures: GB/T 507082012 [S]. Beijing: China Architecture & Building Press, 2012. (in Chinese)
[2] National Design Specification for Wood Construction: ANSI/AF & PA NDS2012 [S]. American Forest & Paper Association, 2012.
[3] MALHOTRA S K. A rational approach to the design of solid timber columns [R]. Applications of Solid Mechanics, Study No7, University of Wateloo, Ontario, Canada, 1972: 311324.
[4] ZAHN J J. Design of wood members under combined load [J]. Journal of Structural Engineering, ASCE, 1986, 112(9): 21092125.
[5] ZAHN J J. Reexamination of the Ylinen and other column equations [J]. Journal of Structural Engineering, ASCE, 1991, 118(10): 27162728.
[6] Engineering Design in Wood: CSA O8609 [S]. Canadian Standards Association, 2010.
[7] NEUBAUER L W. A realistic and continuous wood column formula [J]. Forest Products Journal, 1973, 23(3): 3844.
[8] JOHNS K C. A continuous design formula for timber columns [J]. Canada Journal of Civil Engineering, 1991, 18: 617623.
[9] 王永華,李开禧.用CDC法计算变轴力杆件的临界力[J].重庆建筑大学学报, 2002, 24(3): 4346,52.
WANG Y H, LI K X. The critical load of variedaxialforce beamcolumn calculated by CDC method [J]. Journal of Chongqing Jianzhu University, 2002, 24(3): 4346, 52.(in Chinese)
[10] 余洋,李开禧.不等端弯矩作用下薄壁梁临界弯矩的计算分析[J].重庆建筑大学学报,2004, 26(6): 4043,48.
YU Y, LI K X. Calculation and analysis on critical moment of thinwalled beams under unequal end moment [J]. Journal of Chongqing Jianzhu University, 2004, 26(6): 4043,48.(in Chinese)
[11] 崔佳,谌红荣,龙莉萍.制作及安装误差对冷弯薄壁C型钢轴心压杆承载力的影响[J].工业建筑,2006,36(7):7983.
CUI J, CHEN H R, LONG L P. The effect of facture and fixing error on bearing capacity of coldformed thinwalled C steel column [J]. Industrial Construction, 2006, 36(7): 7983.(in Chinese)
[12] 钟永, 任海青, 娄万里. 木节对规格材抗弯强度影响的试验研究[J]. 建筑材料学报, 2012, 15(16): 875878.
ZHONG Y, REN H Q, LOU W L. Experimental research on the effects of knot on the bending strength of dimension lumber [J]. Journal of Building Materials, 2012, 15(16): 875878.(in Chinese)
[13] BAO V, ARRIAGA F, SOILN A, et al. Prediction of bending load capacity of timber beams using a finite element method simulation of knots and grain deviation [J]. Biosystems Engineering, 2011, 109: 241249.
[14] PABLO G, JUAN O. The utility of lowcost photogrammetry for stiffness analysis and finiteelement validation of wood with knots in bending [J]. Biosystems Engineering, 2013, 114: 8696.
[15] 蘇学良,王振家.木节对板材抗拉强度影响的研究[J].哈尔滨建筑工程学院学报, 1986(3): 1628.
SU X L, WANG Z J. Study of the effect of knots on tensile strength of lumber [J]. Journal of Haerbing Construction Engineering College, 1986(3): 1628. (in Chinese)
[16] CHEN W F. 梁柱分析与设计[M].北京:人民交通出版社,1997.
CHEN W F. Beam column analysis and design [M]. Beijing: People's Communications Press, 1997. (in Chinese)
[17] 潘景龙,祝恩淳. 木结构设计原理[M]. 北京:中国建筑工业出版社, 2009.
PAN J L,ZHU E C. Design principles of timber structures [M]. Beijing: China Architecture and Building Press, 2009: 9. (in Chinese)
[18] 周波.花旗松胶合木轴心受压柱稳定承载力试验及研究[D].重庆:重庆大学, 2016.
ZHOU B. Experimental research on stability bearing capacity of DouglasFir glulam axial compressive column [D]. Chongqing: Chongqing University, 2016. (in Chinese)
(编辑胡英奎)
