干湿复合式空气滤清器压力损失的一维仿真计算
2017-06-26王仁人张庆才
王仁人,刘 芹,张庆才
(1.齐鲁工业大学 电气工程与自动化学院,山东 济南 250353;2.齐鲁工业大学 机械与汽车工程学院,山东 济南 250353)
干湿复合式空气滤清器压力损失的一维仿真计算
王仁人1,刘 芹2,张庆才2
(1.齐鲁工业大学 电气工程与自动化学院,山东 济南 250353;2.齐鲁工业大学 机械与汽车工程学院,山东 济南 250353)
将滤清器简化成由多段不同管径的管道串联而成,建立了一种新型的干湿复合式空气滤清器的串联模型。把非圆形截面管道简化成圆形截面管道来分析,用非圆形截面管道的当量直径来代替圆管直径;把钢丝滤网和滤芯部分简化成多孔介质来分析。整个管路系统的压力损失等于沿程压力损失和局部压力损失之和。所得到的模型是紊流沿程阻力系数λ、局部阻力系数ζ、穿透率K、流体密度ρ、流体平均速度v等的函数。计算结果表明:干湿复合式空气滤清器的压力损失大部分集中在粗滤和精滤部分,且大部分是集中在粗滤部分的钢丝滤网部分,并将计算结果与相关实验以及仿真结果进行对比,验证了模型的合理性。
车辆工程;空气滤清器;压力损失;串联;简化;多孔介质
0 引 言
空气滤清器是内燃机进气系统的空气过滤部件,用于过滤空气中的灰尘和杂质,延长内燃机的寿命。笔者研究的对象为干湿复合式空气滤清器,通过油浴和纸滤芯对空气进行两次过滤。工作时,空气和灰尘自进气口流入后,先进入油浴室,由飞溅的油花将空气中的绝大多数灰尘等杂质吸附,并沉积于油底壳内;然后再经过钢丝滤网过滤,进入到干湿空滤室,再经一级和二级滤芯进一步过滤,保证气缸中进入足量清洁的空气。目前对空气滤清器内部流场的研究主要有实验和数值模拟两种方法[1]。笔者忽略杂质对流动的影响,流动过程中认为流体密度不变是不可压缩单向牛顿流体,具有黏性,紊流,滤网尺寸小、数量多。采用多孔介质进行分析,假设固体构件均匀分布于控制体内,各向同性,把流动管路看成是由不同直径的管段首尾相连而组合成的串联管路。笔者从理论上研究干湿复合式空气滤清器内流动过程产生的压降,建立了干湿复合式空气滤清器压力损失的一维模型。
1 模型建立
1.1 几何模型
笔者研究的柴油机空气滤清器是一种干湿复合式空气滤清器,其结构如图1。该滤清器分为3部分:入口部分、粗滤部分和精滤部分。其中入口部分包括圆形管道、扁形管道和格栅;粗滤器包括油池及钢丝滤网过滤层;精滤器包括精滤器一级滤芯和精滤器二级滤芯。

图1 干湿复合式空气滤清器的结构Fig. 1 Structure diagram of the dry and wet composite air filter
1.2 一维模型
建立如图2的一维串联模型。

图2 干湿复合式空气滤清器的一维计算模型Fig. 2 One-dimensional calculation model of dry and wet composite air filter
图2中,0-1为入口部分的圆管部分,1-2为入口部分的扁形管部分,2-3为格栅以下、油池液面以上、钢丝滤网以下的扁形管部分,3- 4为钢丝滤网部分,4-5为钢丝滤网上部的扁形管部分,5-6为粗滤器出口到精滤器一级滤芯外侧的圆筒部分,6-7为精滤器一级滤芯,7-8为精滤器一级滤芯内侧到精滤器二级滤芯的外侧的圆筒部分,8-9为精滤器二级滤芯,9-10为精滤器二级滤芯内侧轴向到出气口的圆管部分。
1.3 多孔介质模型的建立
1.3.1 钢丝滤网部分多孔介质模型的建立
将钢丝滤网部分简化为多孔介质,用分布阻力来考虑固体构件对动量变换的影响。流体以一定速度穿过多孔介质时的压力损失如式(1)[2]:

(1)
式中:Kj为多孔介质的穿透率,与速度为准线性关系,如式(2):
(2)
式中:αj,βj(j=1,2,3),分别为3个正交坐标轴方向的系数,在各向同性多孔介质中,α=α1=α2=α3,β=β1=β2=β3。
由STAR-CD软件说明书中关于多孔介质参数的设置介绍,知各向同性多孔介质的两个阻力系数α和β的值由式(3),式(4)确定:

(3)
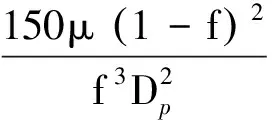
(4)
式中:ρ为流体的密度;f为无量纲量,f=0.5;Dp为多孔介质孔的直径;μ为流体的动力黏度。
笔者的研究都是在常温常压下,即在温度为20 ℃,大气压为1.01×105Pa时,μ=1.789×10-5Pa·s,ρ=1.205 kg/m3。
当流体流动状态为层流时,α=0,当流体流动状态为紊流时,β很小,可以忽略不计。笔者的研究中流体流动状态为紊流,所以在此忽略β。
1.3.2 滤芯部分多孔介质模型的建立
对于滤纸的处理,一般采用多孔介质模型。与一般流体流动情况类似,经过多孔介质的流动也是需要考虑层流和湍流情况的[3]。对于层流,流过多孔介质的流动遵循Darcy定律。对于湍流,可对达西定律修正,在简单、均匀的多孔介质上可使用以下数学模型[4]来求得压降。
(5)
式中:μ为流体的动力黏度;α为黏性阻力系数;C为惯性阻力系数;ρ为流体的密度;v为流体的平均速度;δ为滤纸的厚度。
由文献[5]的滤纸阻力特性实验数据可得

已知滤芯1的厚度为δ1=5.8×10-4m,δ2=4×10-4m,μ=1.789×10-5Pa·s,ρ=1.205 kg/m3。代入得
1/α1=2.77×1010/m2,C1=5.63×105/m
1/α2=4.02×1010/m2,C2=8.17×105/m。
1.4 数学模型
1.4.1 沿程压力损失
圆管紊流的沿程压力损失为[6]

(6)
式中:λ为紊流沿程阻力系数;l为管道的长度;d为管径的直径;ρ为流体的密度;v为流体的平均速度。
对于非圆管的沿程压力损失,用当量直径de来代替相关计算式中的管道直径d,所以流动计算可适用于任意形状的过流断面(流通截面面积A仍以实际截面面积计算)。则当量直径为

(7)
代入得

(8)
1.4.2 管路中管径突然扩大型的局部压力损失
在笔者的研究中,把1-2处的过渡简化成管径突然扩大型,所以局部压力损失[7]为

(9)
1.4.3 管路中管径突然缩小型的局部压力损失
在笔者的研究中,把2-3处的过渡简化成管径突然缩小型,所以局部压力损失[7]为
(10)
1.4.4 串联管路中折管处的局部压力损失
把2-3到3-3过渡处简化为折管,由文献[6]知局部压力损失为
(11)
1.4.5 出口处弯管部分的局部压力损失
弯管的局部损失为
(12)
1.4.6 平均速度的求解
因为流量和截面已知,可由q=vA求得平均速度v。
1.4.7 沿程阻力系数λ的求解

2 压力损失的一维仿真计算
笔者以干湿复合式空气滤清器为例,为了计算其内部所产生的压力损失,提出了上述的串联模型,干湿复合式空气滤清器各个部分的压力损失计算公式如下。
2.1 0-1段的沿程压力损失
见图1中进气口至1-1圆管部分的简化分析可知,因为此段是圆管,所以圆管的沿程压力损失为

(13)
2.2 1-2段的沿程压力损失
见图1中1-2非圆管部分的简化分析,对于非圆管笔者以当量直径de来代替圆管的直径,所以

(14)
2.3 1-2段管径突然变大型的局部压力损失
1-2段的过渡简化为管径突然扩大型来分析,所以局部压力损失为

(15)
2.4 2-3段的沿程压力损失
2-3段为格栅下、油池液面以上、钢丝滤网以下的部分,油池部分可不用考虑,此段分析同1-2段,以扁管的当量直径de来代替圆管的直径,所以
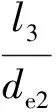
(16)
2.5 2-3段管径突然缩小型的局部压力损失
由入口处的扁管到油面以上扁管的过渡简化为管径突然缩小型来分析,所以局部压力损失为
(17)
2.6 2-3段中折管的局部压力损失
在2-2至3-3管径变化处有两处为折管,折角都为θ=90°,代入ζ3=0.985得
(18)
2.7 3- 4段的局部压力损失
将钢丝滤网简化为多孔介质,则此段的压降为
(19)
已知:f=0.5;ρ=1.205 kg/m3;μ=1.789×10-5Pa·s。
由于钢丝滤网过滤层不是标准的多孔介质,孔的形状也不规则,Dp不能取到精确值,由文献[8]知当Dp=0.008 m时,误差最小。由图1知流体经过钢丝滤网时速度在x、y上的速度分量都为0,即只在z方向上有速度。将以上数值代入式(19)得
(20)
2.8 4-5段的沿程压力损失
钢丝滤网上部非圆管部分的简化分析,利用当量直径来计算,则

(21)
2.9 5-6段的局部压力损失
5-6段为粗滤器出口到精滤器一级滤芯外侧的圆筒部分,由于此段的速度方向是垂直于圆筒,沿程压力损失几乎为0,所以只考虑局部压力损失,垂直进入精滤器后,速度方向碰到精滤器的管壁后180°折回再进入滤芯内,则

(22)
2.10 6-7段的局部压力损失
精滤器一级滤芯的简化分析,对于滤芯一般简化为多孔介质来分析,使用以下数学模型来求得压降,则
(23)
2.11 7-8段的沿程压力损失
即精滤器一级滤芯内侧到精滤器二级滤芯的外侧的圆筒部分,截面为非圆管,用当量直径代替圆管的直径,其他也同圆管的分析:

(24)
式中:d3为精滤器一级滤芯和二级滤芯的半径之差。
2.12 8-9段的局部压力损失
精滤器二级滤芯的简化分析,同滤芯1的分析,将此段简化为多孔介质,则
(25)
2.13 9-10段的沿程压力损失
即精滤器二级滤芯内侧轴向到出气口的圆管部分,因为此段是圆管,所以沿程压力损失为
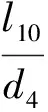
(26)
2.14 精滤器二级滤芯内侧折管的局部压力损失
速度由垂直于轴向到平行于轴向的折角θ=90°,代入ζ4=0.985得

(27)
2.15 出口处弯管部分的局部压力损失
如图1的结构图,出口处弯管角度θ=90°,代入ζ=0.248得

(28)
以笔者所研究的某干湿复合式空气滤清器为例,利用上述计算公式计算其内部流动产生的压力损失。笔者选取的空气滤清器的基本参数见表1。
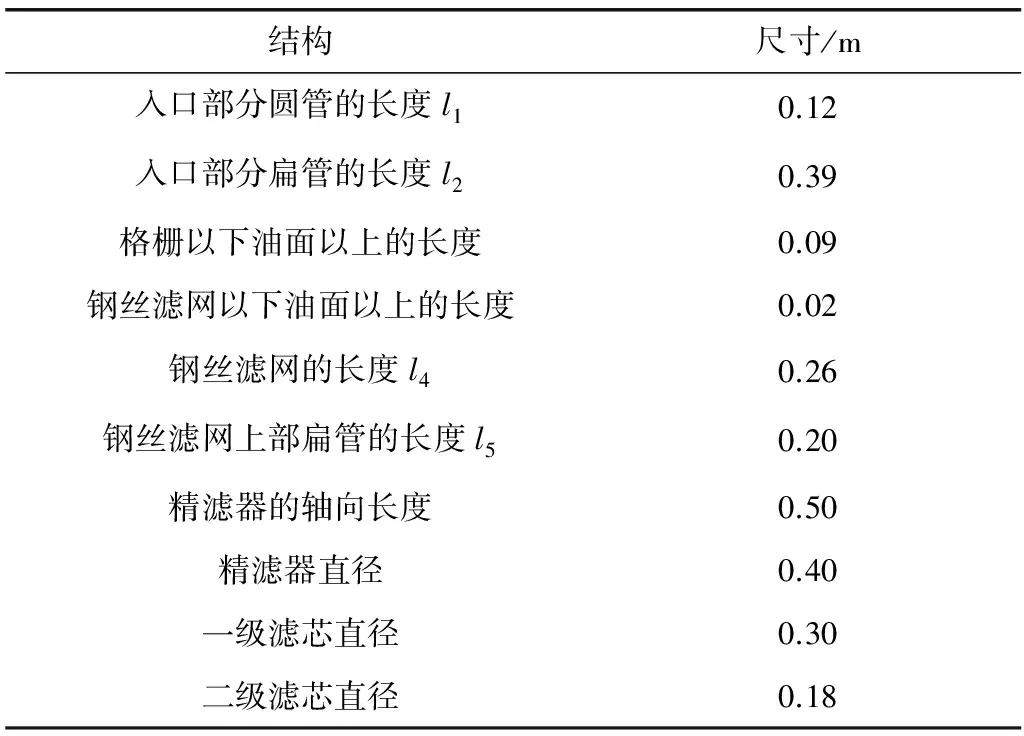
表1 数值计算模型的基本参数Table 1 The basic parameters of numerical calculation model
笔者的研究是在常温下(即t=20 ℃,p=1.01×105Pa)进行,已知空气的密度ρ=1.205 kg/m3,空气的运动黏度υ=1.48×10-5m2/s,空气的动力黏度μ=1.789×10-5m2/s,进气流量q=0.5 m3/s。
各部分的压力损失如下。
入口部分的压力损失为


(29)
代入上述相关数据得出
Δp入口部分=5.4+1.45+240.16=247.01 (Pa)
粗滤部分的压力损失为
Δp粗滤部分=Δpf3+Δpj2+Δpj3+Δpj4+Δpf4=
(30)
代入上述相关数据得出
Δp粗滤部分=249.33+627.6+1 524.54+4 404.4+0.11=6 805.98 (Pa)
精滤部分的压力损失为
Δp精滤部分=Δpj5+Δpj6+Δpf5+Δpj7+Δpf6+Δpj8+
(31)
代入上述相关数据得出
Δp精滤部分=175.31+525.72+0.024+1 125.63+34.05+475.3+119.67=2 455.7 (Pa)
综上,流体在干湿复合式空气滤清器内流动过程产生总的压力损失为沿程压力损失和局部压力损失之和,即
Δp总=p11-p1=∑Δpf+∑Δpj=(Δpf1+Δpf2+
Δpf3+Δpf4+Δpf5+Δpf6)+(Δpj1+Δpj2+Δpj3+Δpj4+Δpj5+Δpj6+Δpj7+Δpj8+Δpj9)
(32)
代入上述各式整理得



(33)
式(33)是严格推导出来的,此式中不含任何经验常数,每个参数都有具体的物理意义,对以后复合式空气滤清器的性能研究具有重要的意义。
代入笔者所研究的滤清器的相关数据得
Δp总=(Δpf1+Δpf2+Δpf3+Δpf4+Δpf5+Δpf6)+(Δpj1+Δpj2+Δpj3+Δpj4+Δpj5+Δpj6+Δpj7+Δpj8+Δpj9)=Δp入口部分+Δp粗滤部分+Δp精滤部分=247.01+6 805.98+2 455.7=9 508.69 (Pa)
将上述结果与相关的实验和数值模拟结果进行对比可知:笔者得到的滤芯部分的公式及其计算结果与谭永南[5]通过实验所拟合的“速度-压降”曲线(Δp=287.54v+196.84v2)基本吻合;贾彦龙[9]对笔者所研究的同类型的干湿复合式空气滤清进行数值模拟得到的压降在9 300~10 000 Pa之间,与笔者的理论计算基本相同。
由上述计算可知,干湿复合式空气滤清器的压力损失大部分都集中在粗滤和精滤部分,且大部分是集中在粗滤部分的钢丝滤网部分。上述结果与王伟,贾彦龙等[8-9]的数值模拟结果相同。文中各部分的压力损失的计算为空气滤清器的改进设计、滤清性能的提高提供了很好的理论依据。
3 结 语
柴油机重型卡车干湿复合式空气滤清器的结构复杂,计算比较困难,一般只能通过数值模拟才能知道内部流动和压损情况。笔者提出了一种新的计算压力损失的方法,简化了结构,将干湿复合式空气滤清器简化为管径不同的串联管路来分析,分析每段的沿程压力损失和过渡段的局部压力损失,建立了简单的多孔介质模型,给出了流体在干湿复合式空气滤清器内流动过程中产生的压力损失的解析式。此公式中不含任何经验常数,每个参数都有明确的物理意义,计算简单方便,对以后干湿复合式空气滤清器的性能研究具有重要的理论意义。
[1] 贾彦龙,韩青,陈宪琳,等.空气滤清器内不可压缩三维湍流流场的数值模拟[J].农业装备与车辆工程,2007(11):30-32.
JIA Yanlong,HAN Qing,CHEN Xianlin,et al.Simulation of incompressible three-dimensional turbulent flow in air filter[J].AgriculturalEquipment&VehicleEngineering,2007(11):30-32.
[2] 韩青,贾彦龙,陈宪琳,等.基于数值模拟的空气滤清器结构优化设计[J].农业装备与车辆工程,2007(10):26-28.
HAN Qing,JIA Yanlong,CHEN Xianlin,et al.The optimization design of air filter structure based on numerical simulation[J].AgriculturalEquipment&VehicleEngineering,2007(10):26-38.
[3] BEAR J.多孔介质流体动力学[M].李竟生,陈崇希,译.北京:中国建筑工业出版社,1983.
BEAR J.DynamicsofFluidsinPorousMedia[M].LI Jingsheng,CHEN Chongxi,Translation.Beijing:China Architecture & Building Press,1983.
[4] 李亨,张锡文,何枫.论多孔介质中流体流动问题的数值模拟方法[J].中国石油大学学报(自然科学版),2000,24(5):111-116.
LI Heng,ZHANG Xiwen,HE Feng.Numerical simulation of fluid flow in porous media[J].JournaloftheUniversityofPetroleum(NaturalScience),2000,24(5):111-116.
[5] 潭永南.空气滤清器的仿真分析与试验研究[D].杭州:浙江大学,2010:20-23.
TAN Yongnan.SimulationAnalysisandExperimentalResearchofAirFilter[D].Hangzhou:Zhejiang University,2010:20-23.
[6] 谢振华.工程流体力学[M].北京:冶金工业出版社,2013:94-106.
XIE Zhenhua.FluidMechanicswithEngineeringApplications[M].Beijing:Metallurgical Industry Press,2013:94-106.
[7] 赵孝保.工程流体力学[M].南京:东南大学出版社,2012:132-134.
ZHAO Xiaobao.FluidMechanicswithEngineeringApplications[M].Nanjing:Southeast University Press,2012:132-134.
[8] 王伟.基于STAR-CD的柴油机空气滤清器内气固两相流研究[D].济南:山东轻工业学院,2010:43- 44.
WANG Wei.StudyofGas-SolidTwo-PhaseFlowinAirFilterforDieselEngineBasedonSTAR-CD[D].Ji’nan:Shandong Institute of Light Industry,2010:43- 44.
[9] 贾彦龙.基于三维紊流数值模拟的空气滤清器结构优化设计[D].济南:山东轻工业学院,2008:34-37.
JIA Yanlong.OptimizationDesignofAirFilterStructureBasedonThree-DimensionalTurbulenceNumericalSimulation[D].Ji’nan:Shandong Institute of Light Industry,2008:34-37.
(责任编辑:谭绪凯)
One-Dimensional Simulation of Pressure Drop of the Dry and Wet Composite Air Filter
WANG Renren1,LIU Qin2,ZHANG Qingcai2
(1.School of Electrical Engineering and Automation,Qilu University of Technology,Ji’nan 250353,Shandong,P.R.China; 2.School of Mechanical and Automotive Engineering,Qilu University of Technology,Ji’nan 250353,Shandong,P.R.China)
The filter was simplified into a series of pipes with different diameters,and a model of a new type of dry and wet composite air filter in series connection was established.The non-circular cross section of pipeline was simplified into a circular cross section of pipeline,and the equivalent diameter of the non-circular cross section of pipe was used to replace the diameter of the circular pipe.Furthermore,the steel wire mesh and filter core in the air filter were also simplified into porous media.The total pressure drop of the pipeline system was the sum of the pressure loss along the flow paths and the local pressure loss.The proposed model was expressed as a function of the frictional resistance coefficientλ,local resistance coefficientζ,penetration rateK,fluid densityρ,fluid velocityvand so on.The results show that most of the pressure drop of dry and wet composite air filter is concentrated in the coarse filter and fine filter,and most of it is concentrated in the steel wire mesh of the coarse filter.And the calculated results are compared with the experimental and simulation results,which verify the rationality of the model.
vehicle engineering;air filter; pressure drop; series; simplify; porous media
2016-01-15;
2017-01-21
济南市高校自主创新计划项目(201004016)
王仁人(1962—),男,山东潍坊人,教授,博士,主要从事内燃机节能与排放方面的研究。E-mail: wrr@qlu.edu.cn。
刘 芹(1990—),女,山东泰安人,硕士,主要从事发动机进气系统方面的研究。E-mail:liuqin_16@126.com。
10.3969/j.issn.1674-0696.2017.06.19
U464.13;TK421
A
1674-0696(2017)06-115-06
