城市轨道交通线网多准则余弦决策支持模型
2017-06-26栾鑫,邓卫,程琳
栾 鑫,邓 卫,程 琳
(东南大学 交通学院,江苏 南京 210096)
城市轨道交通线网多准则余弦决策支持模型
栾 鑫,邓 卫,程 琳
(东南大学 交通学院,江苏 南京 210096)
通过建立城市轨道交通线网方案优选决策多指标评价体系,在考虑AHP和灰色关联分析综合赋权过程基础上,提出应用于轨道交通线网优化的多准则余弦决策支持模型,同时采用苏州市具体案例对模型客观性、公正性和有效性进行了实例验证与研究讨论。研究表明其分析结果科学合理、有说服力。
交通运输工程;轨道交通线网方案;决策支持模型;余弦函数法;多准则评价与优选
0 引 言
城市交通问题根源之一是土地利用的空间布局问题,交通网络不但影响城市发展形态,也对交通需求产生重要影响。随着城市化和机动化水平不断提高,城市公共交通优先发展和公交导向型的交通发展策略越来越受城市规划和决策者青睐。以公共交通为导向的发展模式(TOD)作为一种交通与土地利用有效协调发展方式[1],目前已得到许多国家重视并进行成功实践。轨道交通是城市公共客运交通体系的骨干运输系统,与其他交通方式相比,具有运输量大、快速准点、节约环保、安全高效的独特优势,在集约用地方面也有其他方式无法比拟的优越性[2],对土地利用和城市发展具导向作用。能够进一步缓解城市交通拥挤问题,有效降低对小汽车依赖和不合理使用,实现交通环境健康、有序和可持续发展。
建造轨道交通有利于缓解城市交通压力,合理有效规划轨道线网非常重要;在轨道交通建设中,线网规划方案设计是大规模复杂系统设计过程。而轨道交通线网性能评价是轨道交通发展中的重要和关键环节,因此有必要对城市轨道交通线网规划方案进行科学评价与优选决策,从而使轨道交通线网建设与城市社会经济增长、人口发展以及交通需求滋长紧密结合。目前轨道交通线网评价与优选决策多采用指标权重与评价函数相结合的方法,国内外学者均对轨道交通线网方案评价优选与决策支持模型和方法进行了研究。李俊芳等[3]运用AHP和模糊决策法对城市轨道交通线网规划方案进行了多层次评判;在绿色交通指导原则下,杜胜品等[4]基于信息熵法研究了轨道网络的综合评定;胡启洲[5]在灰色系统理论框架下,评价了城市公交线网的性能特征;Q. ZHANG[6]对灰局势法在轨道交通线网方案决策中展开了具体应用研究。而上述方法均存在一定程度不足,如层次分析法往往相对依赖专家主观判断,进行重要度分析时,客观信息考虑相对欠缺;灰色关联分析重点依靠客观数据差异性,有关专家经验、决策者偏好等主观因素考虑存在缺乏。余弦决策原理在城市公交线网优化排序中也有着实际应用与分析[7]。
基于此,笔者采用AHP和灰色关联分析多指标综合赋权新思路,提出了轨道交通线网多准则余弦决策支持模型。该方法综合考虑了主客观因素,充分保证主观与客观性相结合,从而使方案优选决策支持过程更科学化、合理化,更具有效性、参考实用价值和适用性,通过线网规划待决策方案与理想方案比较,进而得到最佳实施方案。
1 多准则余弦决策支持模型
1.1 余弦决策基础
各评价指标归一化处理过程如下,令
则对于效益和成本型指标,分别有
(1)
(2)
假设理想方案为P*=(g1,g2,…,gm),预选方案为Pi=(ri1,ri2,…,rim);令其在二维空间xoy中对应点分别为(a1,a2,…,am)和(ai1,ai2,…,aim),同时定义理想指标线段oaj指以原点o为起点,以理想方案P*指标值gj为终点aj构成的有向线段,同理可得待决策指标线段oaij;其中指标线段夹角θij(锐角)定义为理想指标线段oaj与决策方案指标线段oaij之间夹角,如图1。

图1 指标线段定义示意Fig. 1 Defined sketch of factor segments
则有

(3)
1.2 多准则决策支持模型
1.2.1 多指标综合赋权模型
为解决多指标间矛盾性引入权重概念,反映了决策人对指标重视程度、各指标属性值差异及可靠程度,是方案优选决策支持过程中的核心问题。笔者综合考虑了主客观因素,应用层次分析(Analytic Hierarchy Process,AHP)和灰色关联分析法(Grey Relational Analysis Method)确定备选决策方案中各评价指标权重,其有效性将在结合具体城市轨道交通线网决策支持中得到详细展现。
传统AHP模型建立主观判断矩阵需进行反复数学计算,过程相对繁琐,增加了模型计算任务与难度;为提高模型应用效率,笔者采用基于一致性判断矩阵的AHP指标赋权模型[8]。
步骤1 建立递阶层次结构,构造判断矩阵
令
A={aij}m×m
式中:aij为第i个指标相对于第j个指标的相对重要度,aij=1(i=j),aij=1/aji。
采用1~9标度法进行各指标(因素)间两两相对比较,其标度含义与判别具体如表1,m个指标通过两两比较后可得判断矩阵A。

表1 指标相对重要度Table 1 Relative importance of indexes
步骤2 一致性矩阵转换

(4)
式中:bij=1(i=j),bij=1/bji,bij=bik·bkj。
由式(4)可得一致性指标对比矩阵B={bij}m×m。
步骤3 计算指标权重
(5)

(6)
灰色系统理论提出了灰色关联分析概念,通过一定方法来求解系统中各指标因素之间数值关系与量化测度[9]。轨道交通线网方案集是一多因素、多层次复杂系统,符合灰色关联分析理论基本要求,在指标值样本量少、数据离散时,可采用灰色关联分析来建立判断矩阵和计算优选决策模型权重。
步骤4 构建初始矩阵
记初始决策矩阵为Y=[yij]n×m,令相对最优方案(理想方案)点为u0=(y01,y02,…,y0m),为消除不同量纲影响,各指标须归一化处理,可得
(7)
步骤5 灰色关联度判断矩阵
根据模糊数学和灰色系统基本理论,采用式(8)度量某方案点ui与u0相关性大小:

(8)

多目标灰色关联度判断矩阵可创建如下
(9)
式中:ξij为方案点ui与相对最佳方案点u0关联度。
步骤6 计算权重值
(10)
利用式(5)和式(10)可综合确定待决策方案中各指标组合权重,如式(11):
(11)
1.2.2 模型构建与说明
在余弦决策理论分析与AHP和灰色关联分析综合赋权模型基础上,通过计算得预选方案Pi与理想方案P*之间加权余弦值为
Di=w1cosθi1+w2cosθi2+…+wmcosθim
(12)
夹角余弦值0≤ cosθij≤1,且 cosθij值随θij增大而减小,故 cosθij值越大表示Pi在指标Gj下的值rij与P*指标值gj越贴近。因此Di值越大,表明Pi越接近P*,即方案Pi越优,从而构建得到问题的多准则决策模型,即余弦决策支持模型。本模型具较强可移植性并创建如下:


(13)
2 线网优选决策多指标评价体系
2.1 决策支持的多目标性
合理的城市轨道交通线网规划不仅能为政府部门提供科学决策依据,还能有效引导城市未来发展。由于轨道交通投资大、建设周期长,在规划建设之前,许多城市都会慎重考虑发展轨道交通特定目的性或能实现的目标。中国多个城市如北京、上海、广州、南京等都根据自身城市特点建立了轨道线网规划评价指标体系,其均充分考虑了网络结构属性、运营客运效果、工程建设实施、经济社会效益与城市发展战略等准则[10]。
在分析已有轨道交通线网评价指标系统和检索相关文献基础上,最终确定从以下4个方面进行考量与决策,包括:轨道交通线网结构特性;规划方案运营与管理;轨道交通建设经济合理性;轨道交通环境保护潜力。这4个目标分别对应于城市规划部门、轨道交通运营管理部门、建设和环保部门,反映了轨道交通规划者和城市决策者发展轨道交通重点考虑内容及期望与侧重点。
2.2 轨道交通线网多目标评价指标体系
多目标评价指标体系是描述评价及决策城市轨道交通线网方案的重要依据与基础,具有多变量、多层次、多属性特点[11],因决策因素众多并交叉在一起,不可能根据单一准则来评判,需从系统协调高度出发统筹考虑与决策分析,全面反映和体现科学、合理、可比、可操作及代表性的评价指标系统建立原则,故构建城市轨道交通线网方案决策多目标评价指标体系是十分重要和必要的。
结合城市发展轨道交通多目标性,充分考虑本文具体案例研究与分析情况,从前述4个方面共确定18个轨道交通线网方案评价指标,创建了轨道交通线网方案决策多目标评价指标体系,其包含15个定量和3个定性指标,定性指标采用1至5评分体系进行计算,5个定性等级代表了差、一般、中等、良好和优秀,具体如图2。

图2 城市轨道交通线网方案决策多目标评价指标体系Fig. 2 Multi-objective evaluation index system of decision-making of URT network schemes
在上述18个指标中,仅指标I13、I23、I24为定性指标;除指标I19、I31、I32、I33为成本型指标外,其余均为效益型指标。
3 案例分析
以苏州轨道交通规划线网方案为具体研究对象,利用式(13)建立的多准则余弦决策支持模型对轨道交通线网进行优选评价与决策分析,同时对模型有效和实用性进行实例验证与应用研究。
3.1 研究设计与数据
与国内其他大城市一样,苏州也面临城市空间规划与管理以及土地和道路使用等方面难题,发展城市轨道交通,可缓解快速城市化和机动化带来的道路拥堵、环境污染等诸多问题。基于上述认识,编制了《苏州市轨道交通线网研究与规划》报告,规划建议了3个备选方案,其均含市郊线S1~S2、市区线U1~U9(图3)。根据图2所示城市轨道交通线网优选决策多指标评价系统,3个规划方案相应阐述及对应具体指标值如表2。
3.2 苏州轨道交通线网优选决策
利用创建的多准则余弦决策支持模型,在AHP与灰色关联分析计算多指标组合权重值基础上,计算3个轨道交通线网方案综合评价值,从而对苏州轨道交通线网各备选方案进行评价和优选决策,其决策支持流程如下:
Step 1 评价指标归一化处理
依据式(1),式(2),对表2中线网方案的评价指标值进行标准归一化处理,得标准决策矩阵R:

Step 2 基于AHP和灰色关联分析的多指标综合权重计算


表3 准则层指标两两判断矩阵与一致性矩阵Table 3 Decision matrix,consistent matrix and weights of criteria

Step 3 测算综合评价值,即计算加权余弦值
由式(3)和式(12)及表2,得出苏州轨道交通线网3个预选方案加权余弦值,如表4。由表4可知,3个线网方案加权余弦值(综合评价值)分别为0.040 95,0.034 73,0.037 90,根据余弦决策理论,Di值越大表明Pi越优,因此3个规划方案优选决策排序为方案1>方案3>方案2,故方案1为最优方案。方案1能够使4个城市重要活动中心建立直接连接,而方案3和方案2在线网规划灵活性上显得相对没有方案1合理,这也是方案1优于方案3和方案2的原因。方案3在轻轨交通线路数、方案总投资和困难施工点数量等方面具相对较强优势,考虑到苏州市内名胜古迹众多,且方案3相对充分考虑了环境保护在城市可持续发展中的作用,故方案3在模型优选决策支持评价过程中较优于方案2。
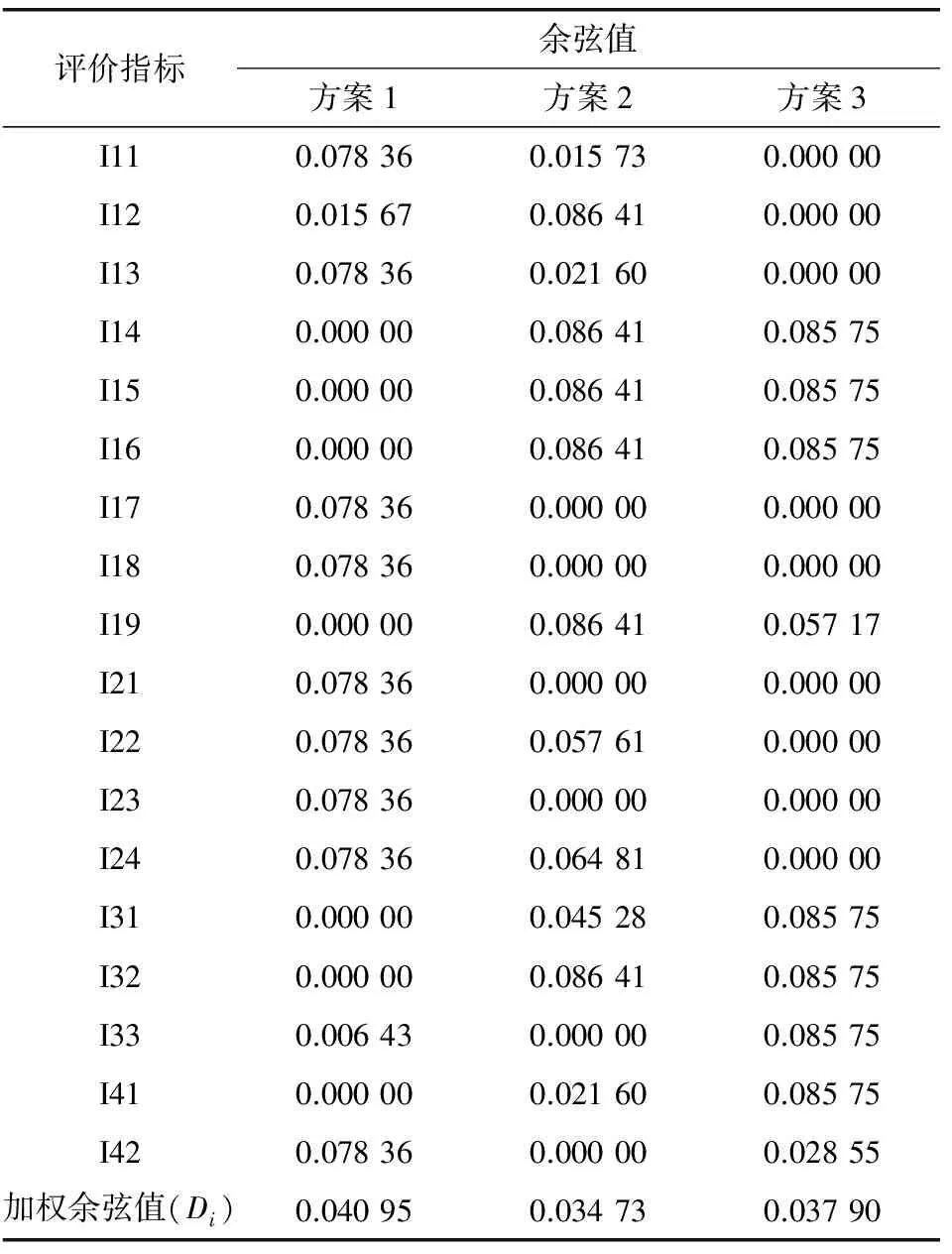
表4 苏州轨道交通线网待决策方案余弦值Table 4 Cosine function values of Suzhou URT network candidate plans
4 结 语
论述了城市发展轨道交通的多目标性,考虑了不同部门对轨道交通期待目标的衡量标准,同时在总结分析其他城市轨道交通线网评价指标体系和查阅相关文献基础上,构建了轨道交通线网优选决策多指标评价体系,涵盖线网结构特性、方案运营与管理、建设经济合理性及环境保护潜力4方面18个指标。
通过基于AHP和灰色关联分析多指标综合赋权模型确定各评价指标组合权重,充分考虑了主客观两方面,改善了单一方法造成的结果偏差,同时结合多准则余弦决策支持模型将多指标评价转化为单指标进行线网方案优选决策支持,并以苏州轨道交通规划方案具体案例对所建模型进行实例验证与应用研究。于2012年开通运营的苏州轨道交通1号线走向与方案1中S1线基本一致;于2013年运营的轨道交通2号线与方案3中S2走向基本相同。这说明在具体线网方案实际建设中,由多准则决策支持模型得出的最优方案在付诸实践中可能会由决策者在最终决策时进行调整与优势整合。
[1] DORSEY B,MULDER A.Planning,place-making and building consensus for transit-oriented development:Ogden,Utah case study[J].JournalofTransportGeography,2013,32(4):65-76.
[2] CAO X J,MOKHTARIAN P L,HANDY S L.The relationship between the built environment and nonwork travel:a case study of Northern California[J].TransportationResearchPartA:PolicyandPractice,2009,43(5):548-559.
[3] 李俊芳,吴小萍.基于AHP-FUZZY多层次评判的城市轨道交通线网规划方案综合评价[J].武汉理工大学学报(交通科学与工程版),2007,31(2):205-208.
LI Junfang,WU Xiaoping.Synthetic evaluation for urban rail transit line network planning scheme based on AHP-FUZZY method[J].JournalofWuhanUniversityofTechnology(TransportationScienceandEngineeringEdition),2007,31(2):205-208.
[4] 杜胜品,熊玲,丁卫东.绿色交通原则指导下的城市轨道网规划综合评价[J].西南交通大学学报,2006,41(3):284-289.
DU Shengpin,XIONG Ling,DING Weidong.Comprehensive evaluation of urban rail transit network planning based on green transportation principle[J].JournalofSouthwestJiaotongUniversity,2006,41(3):284-289.
[5] 胡启洲.城市公交线网的灰色评价及其应用[J].交通运输系统工程与信息,2006,6(2):57-61.
HU Qizhou.A grey-theory-based evaluation with application for urban public traffic network[J].JournalofTransportationSystemsEngineeringandInformationTechnology,2006,6(2):57-61.
[6] ZHANG Q.Research and application of grey situation decision in rail network scheme[J].TransportStandardization,2010(7):36-39.
[7] 胡启洲,张卫华.基于信息熵的公交线网优化方案余弦排序[J].系统工程理论与实践,2008,28(12):121-127.
HU Qizhou,ZHANG Weihua.Cosine prioritizing method for the optimization scheme of public traffic network based on information entropy[J].SystemsEngineeringTheoryandPractice,2008,28(12):121-127.
[8] ZHENG G,JING Y,HUANG H,et al.Application of improved grey relational projection method to evaluate sustainable building envelope performance[J].AppliedEnergy,2010,87(2):710-720.
[9] ASLAN N,SHAHRIVAR A A,ABDOLLAHI H.Multi-objective optimization of some process parameters of a lab-scale thickener using grey relational analysis[J].SeparationandPurificationTechnology,2012,90(4):189-195.
[10] 王艳荣.城市轨道交通线网规划方案评价方法及应用研究[D].北京:北京交通大学,2013.
WANG Yanrong.ResearchonEvaluationMethodandApplicationforUrbanRailTransitNetworkPlanningProgram[D].Beijing:Beijing Jiaotong University,2013.
[11] 刘玉增,钱丙益.轨道交通线网方案比选的多目标格序决策方法[J].交通运输工程学报,2011,11(5):76-82.
LIU Yuzeng,QIAN Bingyi.Multi-objective lattice-order decision-making method of scheme selection for rail transit network[J].JournalofTrafficandTransportationEngineering,2011,11(5):76-82.
(责任编辑:谭绪凯)
Multi-criterion Decision-Making Support Model of Urban Rail Transit Network Based on Cosine Function
LUAN Xin,DENG Wei,CHENG Lin
(School of Transportation,Southeast University,Nanjing 210096,Jiangsu,P.R.China)
Through establishing the optimal decision scheme of multi-index evaluation system of Urban Rail Transit(URT) network,and considering the multi-index combinational weights in virtue of AHP and grey relational analysis methods,the cosine multi-criterion decision-making support model for URT network optimization was proposed.Furthermore,the objectivity,impartiality and validity of the proposed model was discussed and verified by a specific case study in Suzhou.The research indicates that the analysis results of the proposed model are scientific,rational and persuasive.
traffic and transportation engineering; rail transit network planning; decision-making support model; cosine function method; multi-criterion evaluation and optimization
2016-05-09;
2016-07-16
国家自然科学基金项目(51378119;51578150)
栾 鑫(1992—),男,山东潍坊人,博士,主要从事交通运输规划与管理方面的研究。E-mail:xinluan@seu.edu.cn。
10.3969/j.issn.1674-0696.2017.06.15
U491.17
A
1674-0696(2017)06-092-07
