基于粒子群算法建立动态称重补偿器仿真研究
2017-06-26闫子旭麦云飞
闫子旭,麦云飞
(上海理工大学 机械工程学院,上海 200093)
基于粒子群算法建立动态称重补偿器仿真研究
闫子旭,麦云飞
(上海理工大学 机械工程学院,上海 200093)
称重传感器是动态称重的核心,其动态性能直接影响动态称重系统的响应速度与最终结果的精度。为解决动态称重系统的响应速度慢且超调量大的问题,文中采用粒子群算法,建立了系统补偿器模型,并进行模块仿真研究。使用Matlab-Simulink搭建动态称重系统模型与补偿器模型,进行了仿真分析。仿真结果显示,该方法使动态称重系统在响应速度与超调量上得到明显改善,从而证实了粒子群算法对动态称重系统动态补偿的可行性。
动态称重;传感器;补偿器;粒子群算法
称重环节根据称重方式可以分为静态称重与动态称重两类。静态称重指称重过程中,将带测物放在称重系统的托架上,待系统稳定后,测出精确数值。静态称重需要等待传感器达到稳态,无法满足工业上快速测量的要求[1-2]。动态称重应运而生。在工业生产中,需要在机器运转的情况下测量产品质量;同时,运转条件下高精度称重传感器往往具有复杂的精确模型。因此,确定整个称重系统的精确数学模型具有较大的难度[3]。
1 动态称重力学分析
工程上通常根据称重系统结构,以及动态称重过程中的机械振动学理论,将称重系统等效为二阶震荡模型,如图1所示。

图1 动态称重系统力学模型
对系统模型进行力学分析,可以得到模型的力学微分方程为

(1)
其中,M(t)为带测物质量;m为托盘质量,x为称重系统位移;k为系统弹性系数;c为系统阻尼系数。将方程进行拉普拉斯变换,得到该等效模型的传递函数
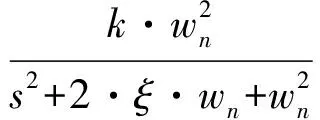
(2)
其中,ξ为系统的阻尼比;ωn为系统固有频率。阻尼比与固有频率直接影响称重系统动态响应的超调量和响应时间,从而影响动态称重效果[4]。但实际的动态称重系统,系数往往并不理想,导致系统动态性能差,从而影响最终动态称重的精度与效率。
2 传感器动态补偿原理
建立动态称重系统补偿模块,改善系统动态响应性能是个理想的选择。输入信号经过称重系统,产生输出信号。由于称重系统工作频带的限制,输出的信号频率成分无法包含输入信号的所有频率成分,从而造成动态误差[5]。因此,添加一个补偿模块,拓宽系统工作频带,使输出信号更加全面的包含输入信号,从而改善系统动态特性。
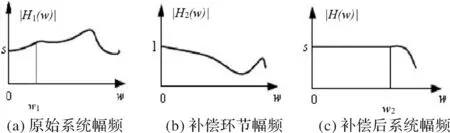
图2 补偿前后系统幅频特性曲线
其补偿原理幅频特性如图2所示,传感器的响应频带为ω1,经过补偿模块后,系统整体频带由ω1拓展为ω2,实现输入信号更多的频率分量通过系统输出,进而实现了动态补偿的效果[6]。
传统补偿模块需要建立在称重系统模型已知的条件下,这意味着称重系统模型的精度直接影响补偿模块的准确程度,从而影响动态称重的效果。高精度的传感器模型往往难以建立,因此本文尝试采用非建模方式-粒子群算法。该方法应用传感器响应曲线,与理想响应曲线对比,建立称重系统补偿模块,是一种有效且运算量较低的方法。
3 粒子群算法原理
粒子群算法(PSO)起源于20世纪90年代,隶属于群体智能算法。粒子群算法的核心思想是在观察动物集群活动行为的基础上,利用种群中的个体对信息的共享使整个种群在问题求解空间中产生由无序到有序的演化运动,从而获得最优解。粒子群算法基于群体智能而进行随机优化,相对其他迭代优化算法而言,二者都是基于种群的迭代搜索进行优化,但是粒子群算法没有交叉、变异算子,而是通过个体之间的协作来寻找最优解[7]。它利用生物群体中信息共享的思想,概念简单、易于实现,同时又有深刻的智能背景,既适合科学研究,也适合工程应用。
4 粒子群算法实现
粒子群算法的根本目标是寻求问题的全局最优解,算法的具体实现是通过跟踪种群的两个极值: 粒子本身所找到的最优解Pbest和群体找到的最优解Gbest来动态调整自己位置和速度[7],完成对问题寻优。其具体步骤如下:
(1)对种群中所有粒子的位置与速度随机初始化。设种群规模大小为N,则初始化生成矩阵
(3)
其中,xij表示粒子位置;vij表示粒子速度;
(2)计算每个粒子的适应度函数;
(3)计算粒子的个体适应度极值Pibest与群体全局适应度极值 ;
PibestMAX(Pi1,Pi2…Pin)
(4)
Gbest=MAX(PI1,PI2…PIt)
(5)
(4)更新粒子位置与速度
vij(t+1)=wvij(t)+c1r1(Pibest-xij(t))+
c2r2(Gbest-xij(t))
(6)
xij(t+1)=xij(t)+vij(t+1)
(7)
(5)判断是否停止迭代。当适应度函数达到预期精度或迭代次数达到上限,停止迭代,否则执行步骤(2)[8]。
5 补偿器实现
基于粒子群算法流程与传感器补偿器的补偿原理,建立动态称重系统补偿方案流程,如图3所示。
补偿模块多以数字滤波器的形式实现。将实际数字滤波补偿器的补偿原理以差分方程形式表示为[9]

(8)


图4 滤波器补偿原理
以传感器的输出y(k)为输入,单位阶跃信号x(t)为输出,应用粒子群算法对补偿器参数进行识别,针对传感器进行多次寻优求解,将结果参数匹配补偿模块系数,对系统中进行补偿[10]。通过对补偿结果进行对比,选取补偿结果最优的系数矩阵
[b0,b1,b2,b3,b4,a1,a2,a3,a4]
从而确定对应参数作为系统补偿器系数。
如何确定补偿系数是粒子群算法要解决的核心问题。应用粒子群算法确定参数,关键是确定方法的适应度函数J与惯性系数w[11]。
适应度函数
(9)

惯性系数直接决定了搜索速度与最终效果。当w取值较大时,有利于全局探寻最佳而不利于局部寻找最佳;当w取值较小时,则对于局部探寻是有意义的[13]。基于以上因素,确定惯性系数迭代公式

(10)
由式(10)所示,惯性系数初始值较大,随着迭代次数增加,逐渐减小,有利于全局最优解的确定[14]。
6 仿真结果
根据上述分析,对动态称重系统以及补偿模块进行仿真分析。在Matlab的Simulink模块中,通过不同参数的设置,对该模型与补偿器进行仿真验证。
由于传感器采用二级模型,对传感器施加单位阶跃激励,产生响应曲线如图6所示。补偿前系统超调量为1.65,稳态时间为10-4数量级,稳态误差为0.02。可以看出补偿前系统单位阶跃响应存在较大的超调量,同时稳态时间不够理想。对于补偿模块,采用4阶模型。Simulink补偿器模型如图5所示。
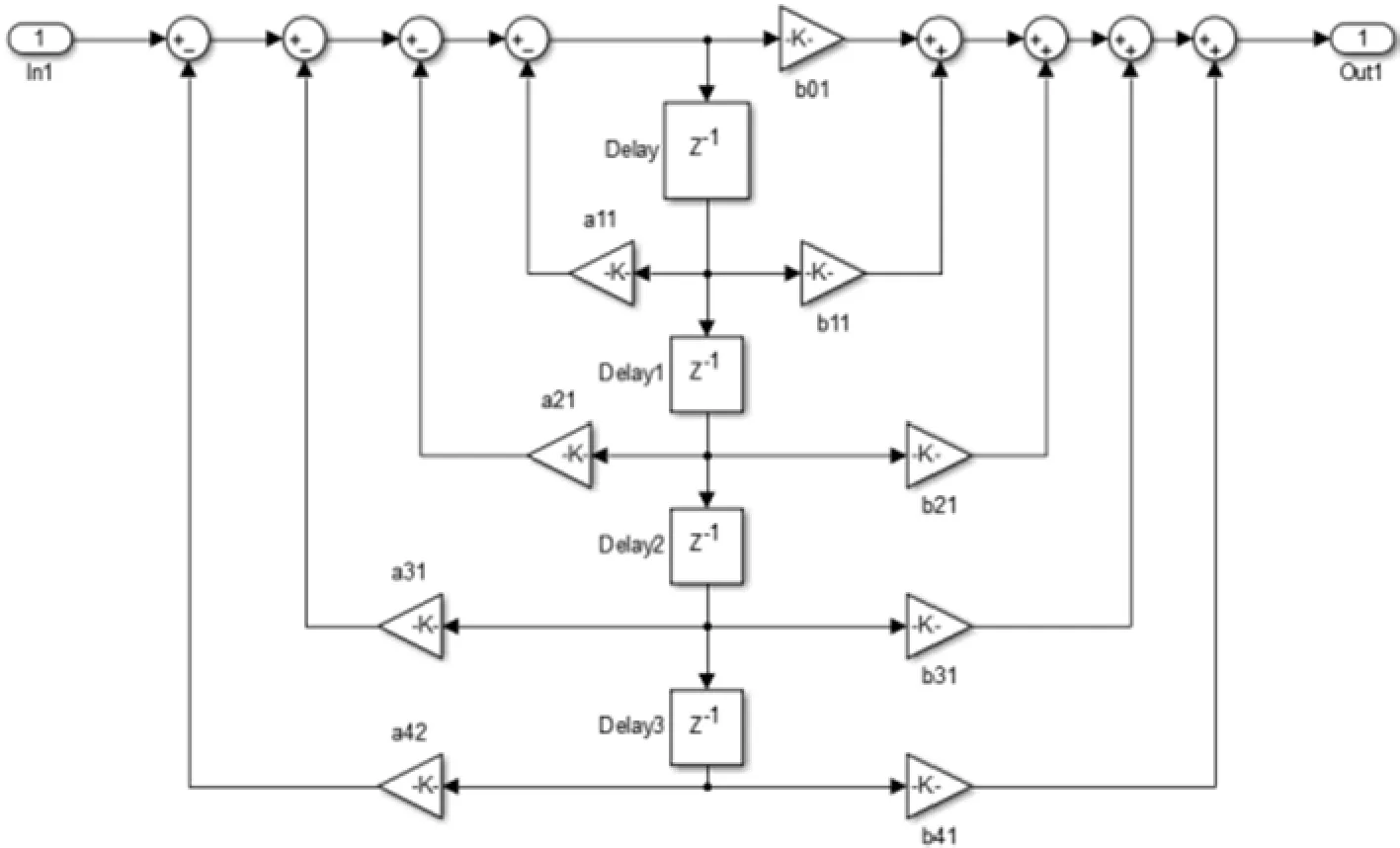
图5 Simulink补偿器仿真模块
由粒子群算法计算,确定补偿模块个参数为[1.872,0.685,0.221,0.803,1.129,1.188,0.940,0.379,0.581],对应补偿器各个参数,对补偿前后分别施加单位阶跃输入,进行补偿前后单位阶跃响应对比。
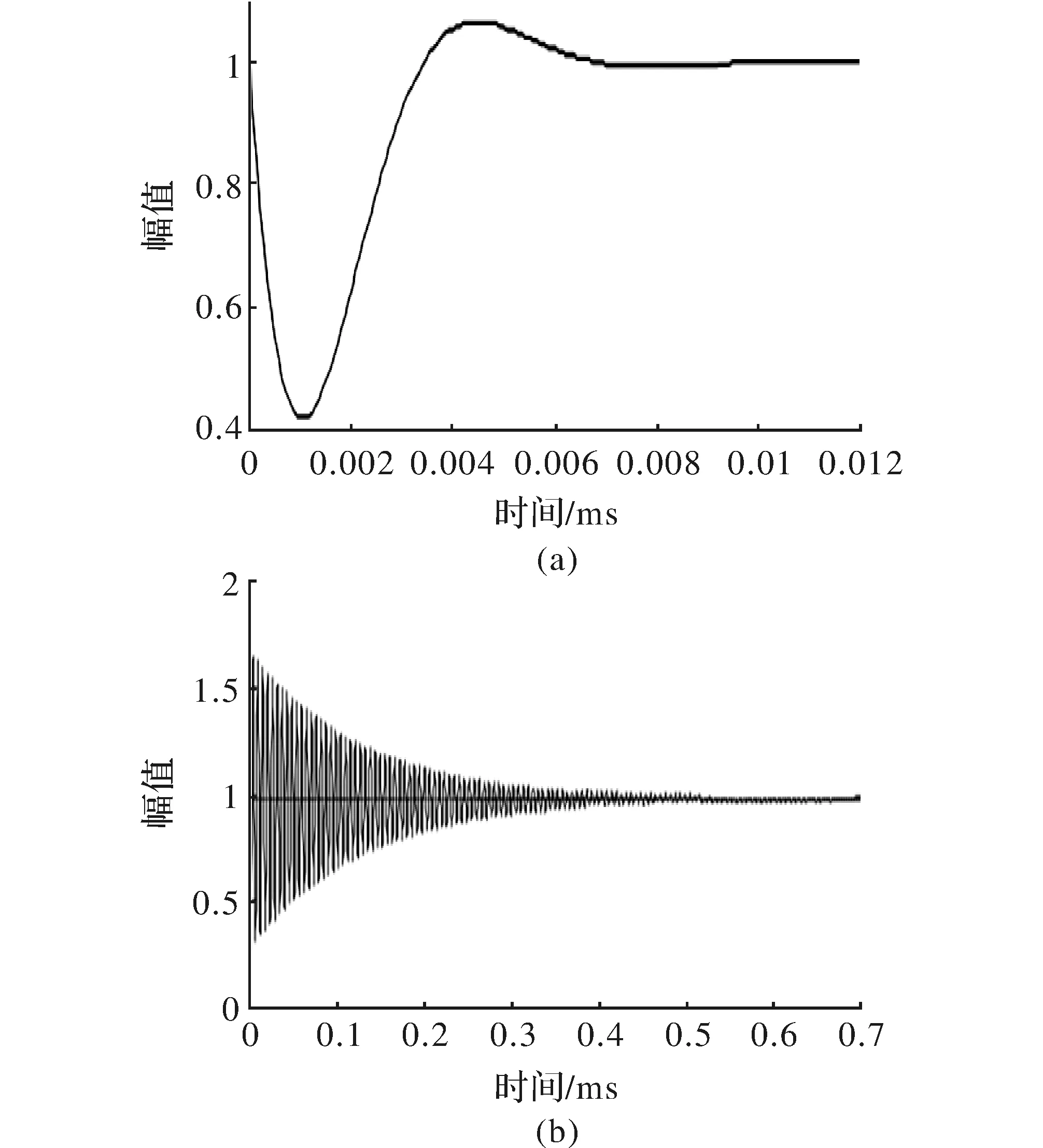
图6 补偿前后响应曲线
由图6可知,图6(a)为补偿前传感器的单位阶跃响应曲线,图6(b)为补偿后的响应曲线。由响应曲线对比可以看出:补偿后系统响应超调量由1.65下降到1.07,超调量与系统震荡得到明显的改善;稳态时间由10-4数量级下降到6.5×10-6,稳态时间得到了数量级的下降;稳态误差由0.02下降到0.000 5以下。对比补偿效果可知,补偿后系统动态性能明显改善,响应曲线在速度与精度上能够较好地反映输入信号。
对比补偿前后的称重系统幅频特性,在幅值误差2%为时,系统工作频带由补偿前的4×105拓宽到1.44×106。理论上系统经过补偿后可以任意拓宽工作频带,但实际进行补偿不可能无限拓宽频带,因为噪声信号通常为高频,工作频道包含高频噪声会导致噪声放大,甚至淹没有用信号,使得测量无法进行。因此,频带拓宽为传感器的2~10倍即可[15]。
7 结束语
为改善动态称重系统性能,对系统添加一个补偿模块,改善系统动态性能。针对以往补偿器过于依赖系统模型这一因素,本文提出采用粒子群算法建立动态称重系统的补偿模块[16]。
首先,与以往的方法相比,粒子群算法无需依赖称重系统模型,即可实现对称重系统动态补偿。该方法利用传感器响应曲线,拟合补偿模块系数,避免了因动态称重模型误差带来的称重误差,从而保证实际应用的可靠性;其次,粒子群算法实现称重系统补偿模块的机理是拓宽系统工作频带,从而改善系统响应特性,最终使动态称重系统响应速度与精度得到提升;仿真结果显示,应用该方法建立的补偿器,使最终响应信号超调量大幅降低,稳态时间得到数量级提高,响应震荡得到明显改善,稳态误差明显降低,输出信号较好地反映了输入信号的特征,从而验证了该方法理论的可行性。
基于以上分析可以得出结论:应用粒子群算法对动态称重系统进行补偿从而改善系统动态性能的方案是可行且有效的,具有一定的推广价值。
[1] 张文娜.压力传感器的辨识建模及动态补偿技术研究[D].长沙:国防科学技术大学,2002.
[2] 郭明威,朱家海.压阻式压力传感器温度误差的数字补偿技术[J].仪表技术与传感器,2008(5):76-77.
[3] 张志通.电阻应变传感器的补偿技术[J].北华航天工业学院学报,2009(1):21-24.
[4] 彭军皓.压阻式压力传感器自动温度补偿系统的研制[D].杭州:中国计量学院,2014.
[5] 黄晓敏.传感器动态特性补偿方法研究及其FPGA实现[D].太原:中北大学,2015.
[6] 孙以材,魏占永,孙新宇,等.压阻型压力传感器的零点温漂及其补偿技术[J].半导体杂志,1999(4):40-49.
[7] 李惠民.运动传感器误差补偿技术研究[D].杭州:浙江大学,2013.
[8] Hayashi C,Shepard S,Winkler I,et al.Nonlinear oscillations in physical systems[M].New York:Mc Graw-Hill,1964.
[9] 卢亮军.基于虚拟仪器的压力传感器自动补偿校正系统[D].武汉:华中科技大学,2007.
[10] Kovacic I,Brennan M J,Lineton B.On the resonance response of an asymmetric duffing oscillator[J].International Journal of Non-Linear Mechanics,2008,43(9):858-867.
[11] 轩春青,轩志伟,陈保立.基于最小二乘与粒子群算法的压力传感器动态补偿方法[J].传感技术学报,2014(10):1363-1367.
[12] 范鑫睿.基于粒子群算法的平衡滑轮补偿法优化设计[D].大连:大连理工大学,2006.
[13] 游晓科,刘观起,杜宝星,等.基于粒子群算法的电力系统无功优化及补偿点的确定[J].陕西电力,2012(4):39-42.
[14] 欧阳承曦.硅压阻式压力传感器高精度温度补偿技术研究[D].成都:电子科技大学,2015.
[15] Virgin L,Davis R.Vibration isolation using buckled struts[J].Journal of Sound Vibration, 2003(10):965-973.
[16] 郭士旭,余尚江,陈晋央,等.压电式压力传感器动态特性补偿技术研究[J].振动与冲击,2016(2):136-140.
Compensator for the Weigh-in-motion System Based on Particle Swarm Optimization
YAN Zixu,MAI Yunfei
(School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)
The weighing sensor is the most important part of the weigh-in-motion system, and the final precision of the system depends mainly on the dynamic characteristics of the sensor. The article proposes the compensator based on the particle swarm optimization to improve the dynamic characteristics of the weigh-in-motion system. Matlab simulation shows the compensator significantly improves the overshoot amount and the response time.
weigh-in-motion; sensor; compensator; particle swarm optimization
2016- 07- 10
闫子旭(1991-),男,硕士研究生。研究方向:机电一体化。麦云飞(1962-),男,副教授,硕士生导师。研究方向:机电一体化等。
10.16180/j.cnki.issn1007-7820.2017.06.013
TP212.6
A
1007-7820(2017)06-046-04
