待定系数法在高中数学解题中的应用

云南省德宏州盈江县第一高级中学 封灵芳

待定系数法是一种基本的数学方法,也是解决数学问题最常用的数学方法之一。那么什么是待定系数法？高中阶段的数学主要是以函数为主线来进行学习的，因此其定义是从函数的角度给出的：一般地，在求一个函数时，如果知道这个函数的一般形式，可以先把所求函数写为一般形式，其中系数待定，然后再根据题设条件求出这些待定系数。这种通过求待定系数来确定变量之间关系式的方法叫做待定系数法。

待定系数法的理论依据是多项式恒等原理，也就是依据了多项式的充要条件是：对于一个任意的a值，都有f(a)=g(a)。或者两个标准多项式中各同类项的系数对应相等。

待定系数法解题的关键是依据已知条件，正确列出含有未定系数的等式。运用待定系数法，就是把具有某种确定形式的数学问题，通过引入一些待定的系数，转化为方程组来解决，要判断一个问题是否用待定系数法求解，只要是看所求解的数学问题是否具有某种确定的数学表达式，如果具有，就可以用待定系数法求解。例如分解因式、拆分分式、数列求和、求函数式、求复数、解析几何中求曲线方程等，这些问题都具有确定的数学表达式，所以都可以用待定系数法求解。

下面我们通过一些具体的例子来体会下待定系数法的应用。

一、利用待定系数法进行因式分解

例1 分解因式：。

分析：这是一个关于的四次多项式，由于次数相对过高，不能使用十字相乘。分组分解法又有困难。经过验证由没有有理根。但是次数是确定的，我们能够根据次数大概猜测其因式分解以后的形式，这个时候我们可以引进待定系数法进行因式分解。

解：设

=

=，

比较等式两边的多项式对应项的系数，列出方程组，得

解该方程，得到

所以。

评析：与这个类型题相似解题的还有解方程、解不等式。如把题目改成解方程，或者解不等式。这两种类型的题型的做法跟本题因式分解方法相同。

二、利用待定系数法拆分分式

例2将化为部分分式之和。

分析：这类型的问题思路基本上跟因式分解类似，首先用未知数表示化为部分分式和以后的形式，展开后，根据分子、分母的多项式分别相等可列出含有未知数的方程组，解方程组，代入所设的部分和即可得结果。

解：

由于

则可设则

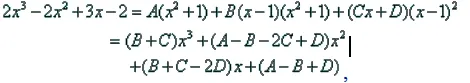
由相等的多项式各项系数相等可列出方程组

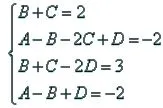
解以上方程组得,故

。

三、利用待定系数法求解曲线方程

例3已知椭圆的离心率为，以该椭圆上的点和椭圆的左、右焦点F1，F2为顶点的三角形的周长为。一等轴双曲线的顶点是该椭圆的焦点，设P为该双曲线上已于顶点的任一点，直线PF1和PF2与椭圆的交点分别为A，B和C，D。求椭圆和双曲线的标准方程（2010年山东高考）。

分析：要用待定系数法求解解析式，首先要知道函数解析式的形式，然后用字母表示出解析式。然后根据题目中给出的已知条件解出未知数，最后写出解析式。

解：设椭圆的半焦距为c，由题意可得：

椭圆的离心率为

根据几何关系，可得到关系式

联立上两式解方程组，得

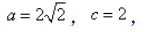
又根据关系式a2=b2+c2，可得b=2。

故椭圆的标准方程为。

由题意可设等轴双曲线的标准方程为，又由于等轴双曲线的顶点是椭圆的焦点，所以有m=2。

评析：用待定系数法求解曲线方程：椭圆、双曲线，抛物线等简单能估计其解析式形式的题型。

四、利用待定系数法求解函数式

例4是否分别存在满足下列条件的函数f(x)：

（1）f(x)是三次函数且

（2）f'(x)是一次函数，

且。

如存在，求出f(x)的表达式；若不存在，说明理由。

分析：首先假设函数存在，用字母设出函数的解析式，利用已知的条件建立方程或方程组，解方程组，求出未知数，写出函数解析式。

解：（1）设，则。

由题意可建立方程式，得

解以上方程组，得

故存在满足f(x)条件的的函数存在，表达式为。

（2）假设f(x)存在，由是一次函数可知f(x)是二次函数，故可设，则。

将f(x)和代入已知条件，得

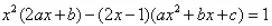
整理得

由等式两边各项系数相等，可建立方程组

解以上方程组可得

所以满足条件f(x)的存在，表达式为。

评析：利用待定系数法求解函数解析式，可以使问题简化。

五、利用待定系数法求数列通项公式

例5已知数列{an}中，a1=1，，设求数列{bn}的通项公式（2010高考全国卷一）。

分析：利用待定系数法求数列的解析式，首先把某些已知条件转化成我们熟知的简单的数列的形式，比如等差数列、等比数列等，用字母表示，然后根据数列的性质，解出未知数，即可得结果。

解：，

则，

即（1）。

则可设，即。通过与（1）式比较，可解得。则。

又有a1=1，故。

故是首项为，公比为4的等比数列，即。

则。

评析：对an+1=can+b(n)，当c=1时，若{bn}为等差数列an+1-an=bn，则，则只需要要用叠加法即可求解。

对an+1=can+b(n)，当c≠1且c≠0时，若b(n)为等差数列，则可设b(n)=xn+y，那么可设，即

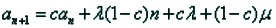
通过所设的式子与原式的对比可设方程组

解方程组得

故数列为等差数列。

最后可以根据等差数列的性质及题目给出的条件求出数列的通项式。

教学本身是一门艺术，教师要唤起学生的兴趣，点燃学生智慧的火花，使学生的探究能力和创新能力得到发展。