十一种技巧破解导数所有难题
2017-06-24陕西省洋县中学何记英
■陕西省洋县中学 何记英
十一种技巧破解导数所有难题
■陕西省洋县中学 何记英
导数的工具性和应用性一直是高考考查的热点,主要题型有:利用导数研究函数的图像和性质进而比较大小关系、求和、求证不等式、求解参数范围、研究零点、求解探索性和新定义问题、研究变化率的实际问题以及简化证明数列求和的不等式等。下面归类分析导数应用的新颖试题。
一、利用导数研究函数的单调性及极值
(1)求a的值及f(x)的单调区间;
(2)∃x∈[0,3],使f(x)<b2,求b的取值范围。
解析:(1)f'(x)=3a x2-3(a+2)x+6,
则f'(2)=0,故a=1。所以f'(x)=3x2-9x+6=3(x2-3x+2)=3(x-1)(x-2)。
令f'(x)>0,则x<1或x>2;
令f'(x)<0,则1<x<2。
所以f(x)的单调增区间为(-∞,1), (2,+∞),单调减区间为(1,2)。
(2)由(1)知f(x)的极小值为f(2)=b +2,f(x)的极大值为
所以f(x)min=b<b2,解得b<0或b>1。故b的取值范围为(-∞,0)∪(1,+∞)。
点评:求函数极值的方法步骤:①求出函数的定义域。②求出函数的导函数f'(x),解方程f'(x)=0,求出x的值。③判定在定义域内导函数为0的点两侧的单调性;并求出在该点的原函数值。④先增后减,为极大值点,先减后增为极小值点;两侧单调性相同,则该点不是极值点。
二、运用导数运算法则构造函数,研究单调性比较大小
例2 已知函数f(x)在R上可导,且∀x∈R,均有f(x)>f'(x),则有( )。

解析:从f(x)>f'(x)这个条件,无法着手,此时我们要借助于选择题中选项的提示功能。结合所学知识分析可知,要引入函数y=ex。由f(x)>f'(x)⇒f(x)-f'(x)
点评:根据导数法则和题设条件,将题设条件合理变形,然后对照法则和导数公式构造新函数,如本题f(x)-f'(x)>0,注意商的导数和y=ex的导数特征可构造h(x)=,研究其性质比较大小。
三、构建辅助函数用导数研究图像求解不等式
例3 已知定义在R上的函数f(x),满足f(x)+2f'(x)>0恒成立,且f(2)=为自然对数的底数),求不等式exf(x)的解集。
点评:超越不等式求解,先化简通过移项变形为h(x)>0,进而构造函数h(x),研究其图像与x轴的交点位置,即可求得不等式的解集,这也是导数的一个重要应用。
四、构建辅助函数研究函数的奇偶性和单调性,求参数范围
例4 设函数f(x)在R上存在导函数f'(x),∀x∈R,有f(-x)+f(x)=x2,在(0,+∞)上f'(x)<x。若f(4-m)-f(m)≥8 -4m,则实数m的取值范围是( )。
A.-2,2[]
B.2,+∞[)
C.0,+∞[)
D.-∞,-2 ( ]∪2,+∞[)
解析:由题设f(4-m)-f(m)≥8-4m和f'(x)<x构造辅助函数g(x)=f(x)-,注意到f(-x)+f(x)=x2,g(-x)所以g(-x)+g(x)=0,即g(x)为奇函数,且g(0)=0。
g'(x)=f'(x)-x<0在(0,+∞)上恒成立,则g(x)为奇函数且在(0,+∞)上为递减函数,于是f(4-m)-f(m)≥8-4m可转化为依据单调性有4-m≤m,所以m≥2,选B。
点评:由题设f(4-m)-f(m)≥8-4m和f'(x)<x及f(-x)+f(x)=x2,可构造辅助函数,证明g(x)为奇函数且在(0,+∞)上单调递减是求解的关键。
五、构造函数用导数证明不等式
例5 已知函数f(x)=(x-1)l nx+ xl n(1-x)。
(1)证明函数f(x)=(x-1)l nx+ xl n(1-x)在定义域内是单调减函数;
(2)设0<a<b<1,求证bb-1(1-b)b<aa-1(1-a)a
因为x∈(0,1),所以l n[x(1-x)]<0,所以f'(x)=l n[x(1-x)]-则函数f(x)= (x-1)l nx+xl n(1-x)在(0,1)上是单调减函数。
(2)注意0<a<b<1和不等式的意义,要证bb-1(1-b)b<aa-1(1-a)a,取对数只需证(b-1)l nb+bl n(1-b)<(a-1)l na+ al n(1-a)成立。
由(1)知函数f(x)=(x-1)l nx+ xl n(1-x)在(0,1)上是单调减函数。
因为0<a<b<1,所以f(a)>f(b),即原不等式成立。
点评:利用导数研究函数的单调性,再用单调性来证明不等式是函数、导数、不等式综合问题中的一个难点,注意试题的特征,对不等式要合理变形,如本题取对数(b-1)l nb+ bl n(1-b)<(a-1)l na+al n(1-a),用已证函数的单调性,从而证得不等式。
六、构建函数,用导数求解不等式恒成立问题
解析:将不等式m [g(x1)-g(x2)]>x1f(x1)-x2f(x2)转化为m g(x1)-x1f(x1)>m g(x2)-x2f(x2)。观察不等式左右结构的对称性,可以构造辅助函数>0。
当x>0时,函数q(x)严格单调递增,即有q'(x)=m x-l nx-1≥0恒成立。
于是h(x)max=h(1)=1,故有m≥1。
因为m∈Z,m≤1,所以m=1。
点评:把不等式m g(x1)-g(x2) [
]>x1f(x1)-x2f(x2)变形为m g(x1)-x1f(x1)>m g(x2)-x2f(x2),使得x1仅出现在不等式左边,而x2仅出现在不等式右边,呈现出不等式左右两边形式一样的对称关系式,便于转化为函数模型去解决问题。
七、利用导数几何意义构造相切条件,确定变量所在位置
例7 已知函数f(x)=x2的图像在点(x0,)处的切线为l,若l也与函数y =l nx,x∈(0,1)的图像相切,则x0所在的区间是( )。

解析:由题意知f'(x)=2x,f(x0)= x20,所以l的方程为y=2x0(x-x0)+x20= 2x0x-x20。因为l也与函数y=l nx的图像相切,令切点坐标为,所以l的方程为,所以因为x1∈(0,1),所以1+令g(x)=x2-l n 2x-1,x∈(1,+∞),则该函数的零点就是x0,排除A、B选项。又因为g'(x)=2x,所以g(x)在(1,+∞)上单调增。又g(1)=-l n 2<0,g(2)=1-l n 22<0,g(3)=2-l n23>0,从而2<x0<。故应选D。
点评:两曲线有公切线,借助导数的几何意义构建两切点之间的关系,再降元构建辅助函数,用导数研究其单调性,用零点存在性定理确定所求变量所在的区间,将导数的几何意义和工具性以及构造函数与函数零点的判断有机地交汇,探究过程耐人回味。
八、利用导数求解函数探索性问题
(1)当m=1时,求函数f(x)的单调性和极值。
(3)某同学发现:总存在正实数a、b(a<b),使ab=ba。试问:他的判断是否正确?若不正确,请说明理由;若正确,请求出a的取值范围。(不需要解答过程)
解析:(1)易求函数定义域为(0,+∞),因为f(x)=x-l nx,,所以当0<x<1时,f'(x)<0,此时f(x)单调递减;当x>1时,f'(x)>0,此时f(x)单调递增。
故f(x)只有极小值,且极小值为f(1)=1。
(2)由(1)知f(x)min=1。因为g'(x)=,所以当0<x<e时,g'(x)>0, g(x)在(0,e]上单调递增,所以g(x)max=
f(x)-g(x)≥f(x)min-故在(1)的条件下,
(3)正确,a的取值范围是(1,e)。
理由如下,考虑数形结合。因为g(x)在 (0,e)上单调递增,在(e,+∞)上单调递减,且当x→0时,g(x)→—∞,当x→+∞时,g(x)→0,所以易知函数g(x)的大致图像如图1所示。

图1
故总存在正实数a、b且1<a<e<b,使得g(a)=g(b),即
点评:利用导数研究单调性可以证明不等式,再结合函数的性质作出其大致图像,借助图像就可以解决探索性问题,这是导数的又一个应用。
九、利用导数研究函数的新定义问题
(1)若函数f(x)与g(x)在公共定义域上具有相同的单调性,求实数m的值。
(2)若函数m(x),m1(x),m2(x)在公共定义域内满足m1(x)>m(x)>m2(x)恒成立,则称m(x)为从m1(x)至m2(x)的“过渡函数”。
(ⅰ)在(1)的条件下,探究从f(x)至g(x)是否存在无穷多个“过渡函数”,并说明理由。
(ⅱ)是否存在非零实数m,使得f(x)是从p(x)至g(x)的“过渡函数”?若存在,请求出非零实数m的取值范围;若不存在,请说明理由。
解析:(1)易知f(x)与g(x)的公共定义域为(0,+∞),且在(0,1)上单调递减,在(1,+∞)上单调递增。又f'(x)则f'(1)=0,即m=-1。经检验,当m=-1时f(x)与g(x)在公共定义域上具有相同的单调性,故所求实数的值为-1。
令F(x)=f(x)-g(x)=x-l nx, x∈(0,+∞),则。故F(x)在(0,1)上单调递减,在(1,+∞)上单调递增,故F(x)min=F(1)=1,因此f(x)-g(x)≥1,即f(x)≥g(x)+1。
令h(x)=g(x)+t,t∈(0,1),则f(x)>h(x)>g(x)在(0,+∞)上恒成立。
故存在无穷多个从f(x)至g(x)的“过渡函数”。
(ⅱ)假设存在实数m,使得f(x)是从p(x)至g(x)的“过渡函数”,则在(0,+∞)上恒成立。令H(x)=f(x)-g(x)=ml nx+x,x∈(0, +∞),则
①当m>0时,H'(x)>0,故H(x)在(0,+∞)上单调递增,且值域为R,此时f(x)-g(x)>0不恒成立,故m>0与假设不符。
②当m<0时,令H'(x)=0,解得x= -m,可知H(x)在(0,-m)上单调递减,在(-m,+∞)上单调递增,故H(x)min= H(-m)=ml n(-m)-m,依题意知, ml n(-m)-m>0,解得m>-e,故-e<m<0;所以,当-e<m<0时,f(x)>在g(x)上(0,+∞)恒成立。
综上可知,不存在非零实数m,使得f(x)是从p(x)至g(x)的“过渡函数”。
点评:新定义的过渡函数,定义域相同且三个函数的大小关系满足m1(x)>m2(x)>m3(x),实质是怎样探究和应用这种不等关系。可以作差构建两个辅助函数研究单调性寻求极值切入,构造这种不等关系,也可以由这种不等关系构建两个辅助函数判断是否有同时存在的条件。
十、利用“二次求导”求解综合问题
当x>1时,h'(x)>0,则h(x)递增,所以h(x)>h(1)=-1。
因为h(3)=1-l n3<0,h(4)=2-l n4>0,故存在唯一x0,x0∈(3,4),使得h(x0) =0。
当1<x<x0时,h(x)<0,x>x0时, h(x)>0,从而g'(x0)=0。
于是,当1<x<x0时,g'(x0)<0,当x>x0时,g'(x0)>0。
g(x)在x=x0时取得最小值,即
由h(x0)=0得l nx0=x0-2,代入上式,得g(x)min=x0,即k<g(x)min=x0。
由于k∈Z,x0∈(3,4),所以kmax=3。
点评:当f'(x)=0无法用初等方程求解时,可二次求导。二次求导与设而不求联袂,化解一次求导函数零点“求之不得”的问题,用零点存在定理估算以及零点适合方程l nx0=x0-2的应用,都是求解超越函数不等式的常用方法。
十一、利用定积分求解数列和的不等式

图2
SABCF,从而=l nn-l n(n-i)。
相加后可以得到:
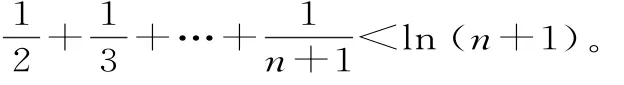
点评:挖掘待证不等式为数列和的不等式左右两边的几何意义,通过构造函数利用定积分的几何意义来解决问题,解法虽然综合性强,但由于数形结合解法直观便于操作。积分法证明不等式是一个新方法、新亮点,很值得品味。
(责任编辑 徐利杰)
