存在交易费用的MAD资本市场的均衡价格

夏艳

（肇庆学院 数学与统计学院，广东 肇庆 526061）

存在交易费用的MAD资本市场的均衡价格

夏艳

（肇庆学院 数学与统计学院，广东 肇庆 526061）

对仅含风险资产且存在交易费用的均值-绝对偏差资本市场，给出了最优投资组合的求解方法，并导出了一个简洁易用的计算均衡价格的公式．

交易成本；MAD资本市场；均衡价格；最优投资组合

0 引言

1952年，Markwitz率先提出了MV模型，首次将数理统计方法应用于投资组合选择的探讨中，为现代投资组合理论研究奠定了重要的基础.到20世纪60年代初，美国学者William Sharpe[1]、John Lintner[2]和Jan Mossin[3]等人在研究资产组合理论的基础上，得出了著名的资本资产定价模型.自此之后，不少学者开始积极探讨和研究均衡价格的存在性问题，但直到20世纪末，绝大部分分析均衡价格的文献都是建立在MV框架下.MV框架下的投资组合模型是一个含参数的大规模二次规划问题，由于其过于严格的假设以及用方差衡量风险的局限性，导致其在市场上的实际应用受到局限.后来，Konno[4]和他的团队提出了均值-绝对偏差模型，即MAD模型，用绝对偏差衡量风险，有效地解决了数据繁杂且应用受限等难题.

在实际投资过程中，无论是买进证券还是卖出证券，每一位投资者都必须支付一定的交易费用，这笔费用的支付，对投资者的最终收益和投资策略都会产生直接且重要的影响，尤其是当资金数量相对较少时，资金的分散有可能引起无法接受的交易成本.由此看来，将交易费用引入到投资组合模型中是非常有必要的，国内学者陈志平[5]等也研究了MV框架下带交易费用的均衡价格问题.本文在不允许卖空的情况下，用均值衡量收益，用绝对偏差度量风险，并引入了比例交易费用，建立含风险资产的MAD资本市场框架，分析最优投资组合的求解过程，探讨均衡价格的显式表示方式.

1 存在交易费用的MAD资本市场模型

假定MAD资本市场中有n种风险资产(S1,S2,…,Sn),其中资产Sj的收益率Rj在T个时间段内的样本观测值分别为rj1,rj2,…,rjT,则Rj的数学期望rj为

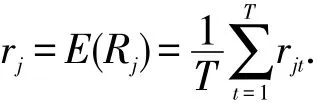
假设初期资产Sj的单位价格为Pj(j=1,2,…,n),市场上共有m个投资者Ii(i=1,2,…,m).若投资者Ii在初期拥有资产Sj的数量为则初始投入的资产总值为

用xij表示投资者Ii在交换后所拥有的资产Sj的数量，假设交易费用为比例交易费用，比例系数为k,则交易费用为交换前后资产总值保持不变，xij应满足下列条件：

投资者Ii在投资组合Xi=(xi0,xi1,…,xin)下的期望收益率为

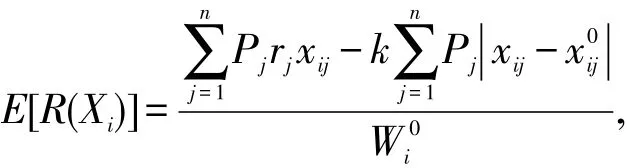
绝对偏差为

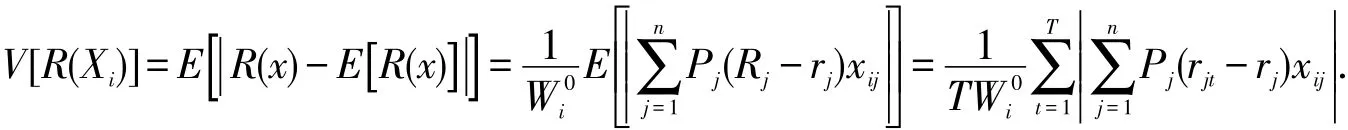
若给定预期收益率ρ,存在交易费用的MAD模型为

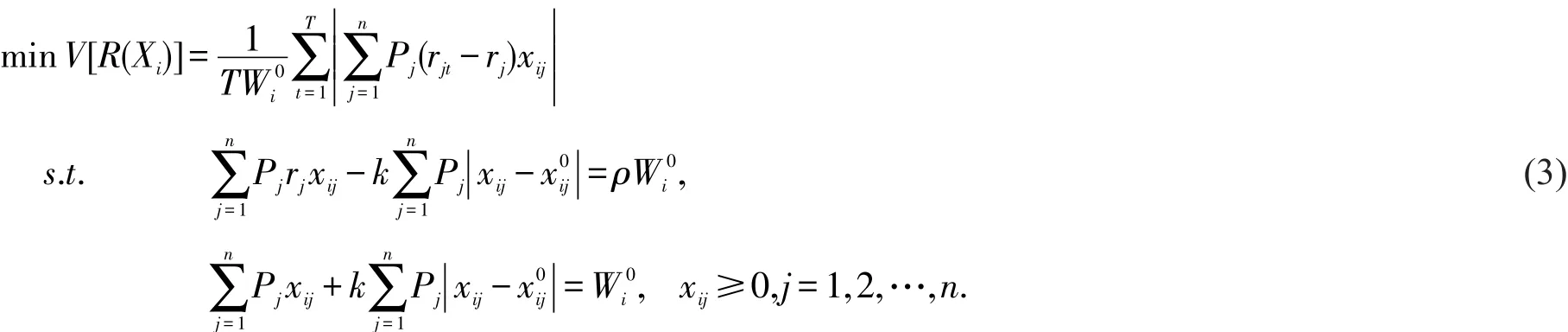
2 最优投资组合

存在交易费用的MAD模型是一个非光滑的线性规划问题，在求解时必须要进行转化.对于特定的投资者Ii而言，不妨记表示该投资者初期投资在资产Sj上的资金比例，类似地，可记则模型（3）可以改写为

引入非负辅助变量vt和wt,满足

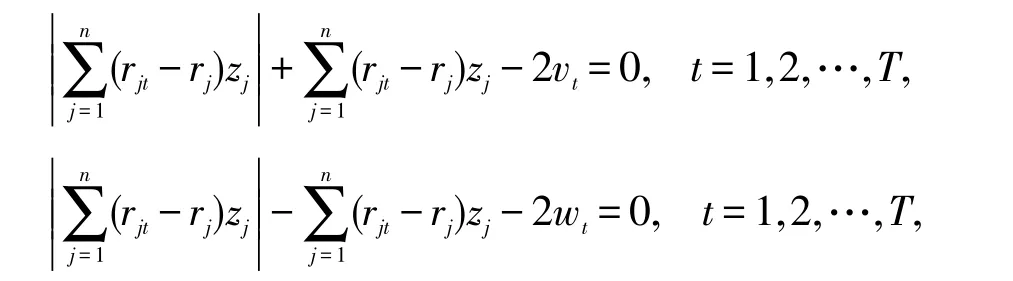
则有

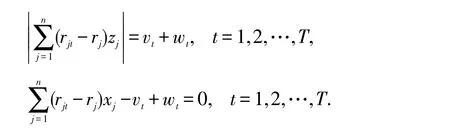
那么投资者的最优投资组合问题（4）可转换为

同理，可引入非负辅助变量pj和qj,去除约束条件中的绝对值项，得到与（5）等价的模型

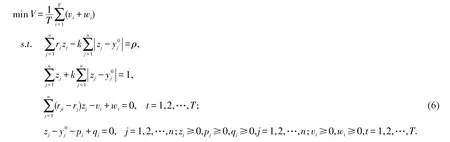
这是一个标准的线性规划问题，可以采取单纯形法求解.不妨记最优化问题（6）的最优解在决策变量上的取值为则根据模型（3）和模型（4）的关系可知：存在交易费用的MAD模型的最优解为

3 均衡价格

下面将导出计算能使市场供需平衡的非负均衡价格向量(P1∗,P2∗,…,Pn∗)的具体公式.设资产Sj在市场中的总量为要使每种资产的总供给等于总需求，则存在交易费用的MAD模型最优解（7）必须满足

于是得到

根据式（1）和式（9），得到

其中a=(a1,a2,…,an)T,b=(b1,b2,…,bn)T.

将系数矩阵进行行初等变换

因此，

联立式（1）和式（12），得

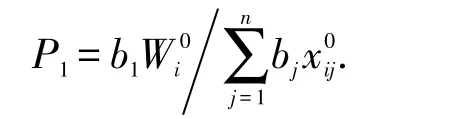
因此均衡价格为

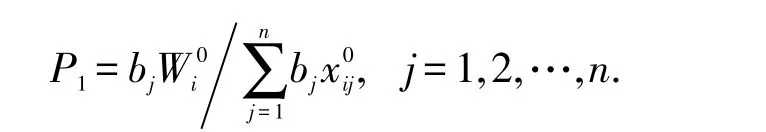
也就是说，含交易费用的MAD资本市场的均衡价格并不唯一，可用最优投资组合表示，这对均衡价格体系是一个有效的补充.

[1] SHARPE W F.Capital asset prices:a theory of market e-quilibrium under condition of risk[J].Journal of Finance,1964,19:425-442.

[2] LINTNER J.The evaluation of risk assets and the selection of risky investments in portolio choice[J].Review of Economics and Statistics,1965,47:13-37.

[3] MOSSIN J.Equilibrium in capital asset market[J].Econometrics,1966,34:768-783.

[4] KONNO H,SHIRAKAWA H.Equilibrium relation in the mean absolute deviation capital market[J].Financial Engineering and the Japanese Markets,1994,1(1):21-35.

[5] 陈志平,王懿.均值-ES框架下带交易费用的资本资产市场中均衡价格的存在性与确定[J].系统与科学,2011,31(5):519-

533.

The Equilibrium Price in the MAD Market Including Transaction Costs

XIAYan

（School of Mathematics and Statistics,Zhaoqing University,Zhaoqing,Guangdong 526061,China）

The solution method of optimal portfolio has been given,and an explicit formula for the equilibrium price is derived from the mean-absolution deviation capital market with risk assets,in which transaction costs are taken into account.

transaction costs;MAD model;equilibrium price;optimal portfolio

F830.9

A

1009-8445（2017）02-0015-04

（责任编辑：陈 静）

2016-12-07

广东省教学质量与教学改革工程建设项目（201550）

夏 艳(1980-)，女，湖南南县人，肇庆学院数学与统计学院助教,硕士.