二进制猫群算法在大规模MIMO天线选择中的应用*

2017-06-23李淑梅庄铭杰

电讯技术 2017年6期

关键词：信道容量二进制复杂度

李淑梅,庄铭杰

(1.华侨大学工学院，福建泉州 362021；2.福建省物联网科学研究院，福建泉州 362000)

二进制猫群算法在大规模MIMO天线选择中的应用*

李淑梅1,庄铭杰**

(1.华侨大学工学院，福建泉州 362021；2.福建省物联网科学研究院，福建泉州 362000)

在多输入多输出(MIMO)系统中，天线选择技术平衡了系统的性能和硬件开销，但大规模MIMO系统收发端天线选择复杂度问题一直没有得到很好的解决。基于信道容量最大化的准则，采用两个二进制编码字符串分别表示发射端和接收端天线被选择的状态，提出将二进制猫群算法(BCSO)应用于多天线选择中，以MIMO系统信道容量公式作为猫群的适应度函数，将收发端天线选择问题转化为猫群的位置寻优过程。建立了基于BCSO的天线选择模型，给出了算法的实现步骤。仿真结果表明所提算法较之于基于矩阵简化的方法、粒子优化算法具有更好的收敛性和较低的计算复杂度,选择后的系统信道容量接近于最优算法，非常适用于联合收发端天线选择的大规模MIMO 系统中。

多输入多输出；天线选择；二进制猫群算法；信道容量；粒子群优化算法

1 引言

大规模多输入多输出(Multiple Input Multiple Output，MIMO)技术通过在接收端和发射端配置多根天线，以获得系统分集增益和复用增益，在不增加带宽的情况下能够成倍提高信道容量和传输可靠性[1-2]。使用大规模MIMO技术是未来移动通信系统的必然趋势，而伴随着天线数目增加，相应的射频链路数目也会增加，从而在加大系统成本的同时给系统信号处理带来了巨大计算压力。此外，天线间的相互干扰也会加重[3]，这些都使得天线选择成为必然。天线选择的最优算法是穷举法[4]，它需要从所有可能的收发端天线组合中挑选出一种组合使得信道容量最大。在大规模MIMO系统中穷举选择最优算法的计算复杂度非常高。因此，各种单端天线选择算法相继被提出。这些算法在损失部分容量情况下，都在一定程度上降低了天线选择的计算复杂度。

为了进一步提高天线选择系统的性能，文献[5]提出了收发端联合天线选择(Joint Transmit and Receive Antenna Selection，JTRAS)算法，容量效果很好，但是复杂度依旧很高，不能满足实际需要。许多学者相继提出各种降低复杂度的收发端联合天线选择算法[6-7]，在降低复杂度的同时保持较高信道容量。然而，对大规模MIMO系统的天线选择这些基于矩阵简化算法难以胜任，天线选择的计算量仍然偏大。目前将天线选择与群智能算法结合也是探索天线选择技术的一个发展方向。文献[8-9]分别将蚁群算法和遗传算法应用于天线选择当中，大幅度降低了计算复杂度。文献[10]提出了一种基于粒子群的天线选择算法，仿真结果表明该算法能大幅度减少计算复杂度，容量效果接近最优算法。文献[11]提出了一种快速收发端联合天线选择算法，并通过循环移位的方式进行种群初始化，进一步加快了收敛速度。文献[12]针对二进制粒子群算法的收敛性问题，提出了一种改进的二进制粒子群收发联合天线选择算法，研究结果表明改进后的算法具有较好的收敛性。

猫群(Cat Swarm Optimization,CSO)算法[13]涉及参数少，收敛速度快，而且具有较好的全局探测和局部搜索能力，现在主要应用于函数优化问题，并取得了很好的效果。文献[14]提出了一种离散二进制猫群算法，对一些基准函数测试显示该算法收敛速度快的同时，计算精度有明显提高。本文基于信道容量最大化的准则，结合二进制猫群(Binary Cat Swarm Optimization，BCSO)算法，利用跟踪模式和搜寻模式交互来求解全局最优的特点，进一步研究了基于BCSO算法的天线选择模型，提出将二进制猫群算法应用于天线选择的过程中，通过BCSO算法的迭代过程来寻找最优天线子集,同时对基于二进制粒子群(Binary Particle Swarm Optimization,BPSO)算法的收发端联合天线选择算法(简称BPSO JTRAS)和递增算法进行性能对比分析。仿真结果表明BCSO JTRAS的收敛性优于BPSO JTRAS，信道容量接近最优算法即穷举法，并且容量效果优于BPSO JTRAS和递增算法。

2 基于BCSO的天线选择

2.1 基于容量最大化的天线选择

基于容量最大化的天线选择，就是从所有的天线集合中选取性能最好的天线子集进行信号的发送和接收。假设系统有Nt根发射天线，Nr根接收天线，收发两端已知信道状态信息，发射机选取Lt根天线发射信号，接收机选取Lr根天线接收信号，即从信道矩阵H中挑选出所期望的最优子信道矩阵HLr×Lt，矩阵内元素hij表示第j根接收天线与第i根发射天线间的信道衰落系数，它服从均值为0、每维方差为1的复高斯随机过程。ρ为接收端的平均信噪比，ILr为Lr×Lr的单位矩阵。当发射端选择的每根发射天线等功率发射信号且互不相关，则天线选择后的信道容量计算式为

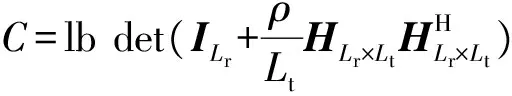
(1)

2.2 二进制猫群算法的天线选择模型

把BCSO算法应用到天线选择中时，式(1)的信道容量表达式作为适应度函数。在猫群算法中，每一只猫的状态信息由四部分组成，即猫的位置、速度、标志位和适应度值。对应的第i只猫可描述为

Cat(i)={location[],velocity[],flag,fitness}。

定义两个二进制字符串QT和QR分别表示发射端和接收端天线选择的状态：

X=[QT,QR]。

Cat(i).location[]=[QT,QR]。

应用式(1)，猫的适应度表示为

Cat(i).fitness=C。

(2)

在猫群算法中，根据交互率将种群随机分为搜寻模式或跟踪模式，标志位为0表示当前猫处于搜寻模式,标志位为1表示当前猫处于跟踪模式。

2.2.1 搜寻模式

搜寻模式中定义了3个基本要素：记忆池、变化域、变化数[13]。记忆池定义为每一只猫搜寻记忆的大小。变化域是指每一维改变的范围，在算法开始之前设定。变化数是一个 0～(Nr+Nt)的随机值。搜寻模式可分为以下4步：

(1)复制j份当前猫的副本放在记忆池中；

(2)对记忆池中的每个副本，根据变化域和变化数，在对应位置维度上取它的补码，用新位置代替原位置；

(3)计算记忆池中所有副本的适应度值；

(4)选择适应度值最高的副本来代替当前猫，完成猫的信息更新。

2.2.2 跟踪模式

(3)

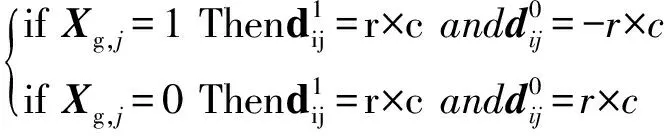
(4)

式中:r为[0,1]之间的随机取值，w为惯性权重，c为常数，下标g记录下目前种群中找到全局最优解的猫。速度更新公式为

(5)

种群位置发生改变的概率通过参数t来定义，t取值范围[0,1]，计算公式为

(6)

位置更新公式为

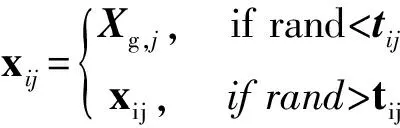
(7)

2.3 BCSO JTRAS的实现步骤

Step 1 设置相关参数，包括种群数目、迭代次数、发送和接收的天线数目及所选择的天线数目、记忆池、变化域、变化数、交互率等。

Step 2 种群初始化。随机生成(QT+QR)个二进制数(要求QR中有Lr个1，QT中有Lt个1)作为每一只猫的位置编码，随机产生(QT+QR)维的速度值，并根据交互率随机设定种群中一部分猫处于跟踪模式，另一部分处于搜寻模式。按式(1)计算种群适应度值。

Step 3 记录适应度最大的猫为当前最优解。

Step 4 根据每只猫所处模式，按照相应的规则完成位置更新，新位置中QT和QR中1的数目分别等于Lt和Lr，否则通过随机强制转换使得1的数目符合条件。

Step 5 根据每只猫所处的模式，按照相应规则完成速度、适应度值的更新操作。

Step 6 按式(1)计算所有猫的适应度值，记录适应度最大的猫为当前的最优解。

Step 7 若满足最优解或达到迭代次数，结束BCSO JTRAS，输出全局最优解；否则，转Step 4继续执行。

3 BCSO JTRAS性能分析

3.1 算法收敛性比较

根据上述所提出算法，对于发射端12选择3和接收端12选择4的 {12,3;12,4} MIMO系统，信噪比(Signal-to-Noise Ratio，SNR) 为10 dB,BCSO的种群大小为20，迭代次数为400，记忆池大小为5,变化域取值为0.2,交互率为0.2，变化数为0到收发天线数目之间的随机值，BPSO的种群大小同样为20，迭代次数为400，速度更新公式的系数c1、c2取值为2[11]。图1给出了采用计算机仿真对BCSO JTRAS和BPSO JTRAS两种算法的收敛性的对比曲线图。从图1中可以看出BCSO JTRAS的收敛性要好于BPSO JTRAS，BCSO JTRAS大约在迭代次数为120次时就收敛于稳定的系统容量值13.75 bit/s·Hz-1，而BPSO JTRAS需要将近350次才近似收敛于13.40 bit/s·Hz-1，而且还不稳定。可见，BPSO JTRAS算法要花费更多的时间进行跟踪和天线选择。从图1仿真结果可看出采用BCSO JTRAS的系统容量要好于BPSO JTRAS。

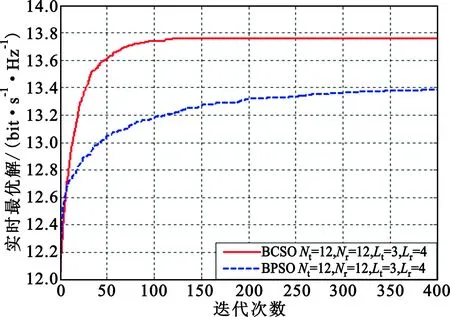
图1 SNR=10 dB时最优解收敛曲线图

3.2 算法容量比较

容量累积分布是对所有瞬时容量的概率统计。以50%中断概率容量来分析系统的平均容量大小，因为此传输速率的中断与不中断的概率是一样的，相当于平均值。图2在Nt=Nr=6，Lt=Lr=2，BCSO和BPSO种群大小都为20，迭代次数为60，SNR取值为10 dB，其他参数取值和图1相同的情况下，给出了最优算法、BCSO JTRAS、递增算法和BPSO JTRAS 4种算法的容量累积分布函数图。从图中可发现BCSO JTRAS的容量累积分布函数曲线比BPSO JTRAS和递增算法更加接近最优算法，即在同样输出信噪比情况下，按50%中断概率计算系统平均容量，BCSO算法要优于BPSO算法和递增算法。

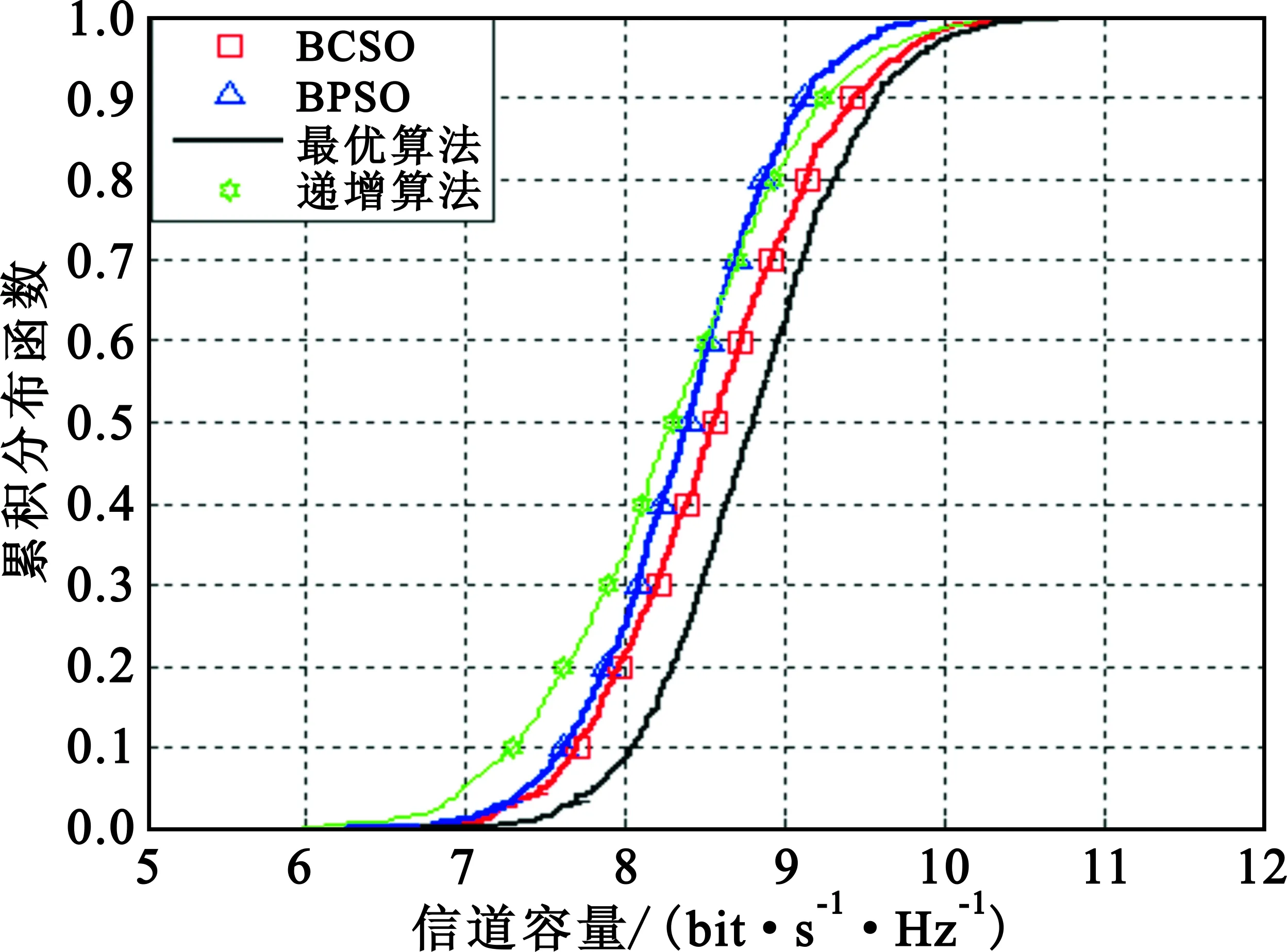
图2 SNR=10 dB各种算法容量累积分布图

在Nt=Nr=6，Lt=Lr=2，除了SNR的取值变为0～20 dB，其余参数取值和图2相同的情况下,针对最优算法、BCSO、递增算法和BPSO 3种算法，图3分别给出了它们50%中断概率的平均容量性能随SNR变化的曲线图。从图3中可以看出，在不同的SNR下，采用BCSO JTRAS的系统容量要优于BPSO JTRAS算法。在同一信道容量(C=13 bit/s·Hz-1)情况下，BCSO JTRAS比BPSO JTRAS可多获得0.2～0.3 dB的信噪比增益；而在同一信噪比(SNR=16 dB)情况下，BCSO JTRAS的容量比BPSO JTRAS高出0.2 bit/s·Hz-1，比递增算法高出0.2 bit/s·Hz-1。

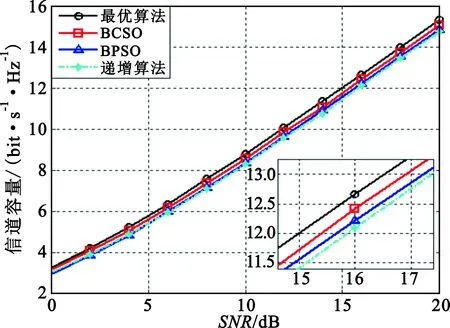
图3 不同信噪比下各种算法容量比较

综上所述，BCSO JTRAS比BPSO JTRAS收敛速度更快，因此，BCSO JTRAS的迭代次数比BPSO JTRAS少，能有效地降低天线选择算法的复杂度。此外，在相同信噪比条件下，BCSO JTRAS的平均容量效果好于BPSO JTRAS和递增算法，而且更加接近最优算法。

4 算法复杂度分析

Times=P×T。

式中：P为种群大小，T是达到收敛时迭代的次数。

表1列出了最优算法、BCSO和BPSO[9]3种天线选择算法计算复杂度，可看出BCSO JTRAS的复杂度明显比最优算法的复杂度低，特别是当天线数目较大时，最优算法的复杂度成指数增长，而BCSO JTRAS的复杂度增加变化不大。此外，由于BCSO JTRAS比BPSO JTRAS的收敛速度更快，在相同种群大小的情况下，BCSO JTRAS的计算复杂度要比BPSO JTRAS低。

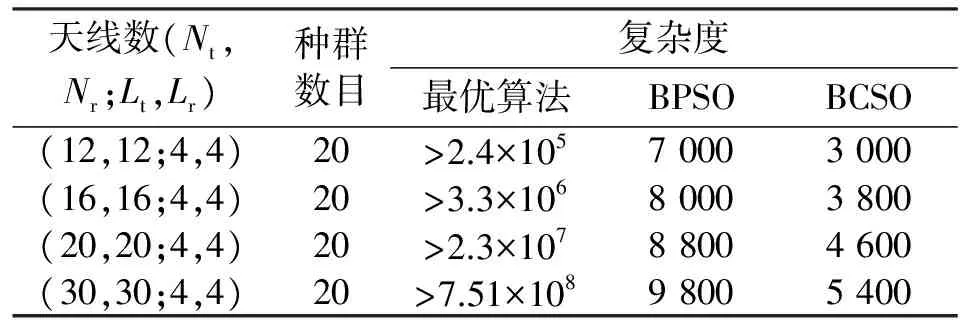
表1 各算法复杂度比较Tab.1 Complexity comparison between various algorithms

5 结束语

猫群算法是近年来新提出的一种群智能算法，它通过搜寻、跟踪两种模式交互迭代能够很好地实现全局探测和局部搜索。本文将猫群算法应用于天线选择当中，结合天线选择的特点，采用离散的二进制猫群算法来模拟天线选择过程。同时，还与基于粒子群的天线选择算法进行对比分析，仿真结果均显示，基于离散二进制猫群算法的天线选择具有更快的收敛速度，且性能比基于粒子群的天线选择算法更加接近最优算法。对于大规模MIMO系统，基于离散二进制的猫群算法在天线选择上的准确率和在算法的效率方面优势明显，具有良好的应用前景。对猫群算法进一步改进，并将其应用于无线通信的其他领域也值得研究。另外，在后续研究中，我们也可以参考文献[15]对粒子种群的初始化进行改进，并改进适应度函数，进一步加快基于二进制猫群的天线选择算法的收敛速度。

[1] BASHAR F,ABHAYAPALA T D.Performance analysis of spatially distributed MIMO systems[J].IET Communications,2016,11(4):566-575.

[2] 李洁,李双志,穆晓敏,等. 基于天线选择技术的大规模下行MU-MIMO系统能效分析[J].电讯技术,2014,54(9):1270-1274. LI Jie,LI Shuangzhi,MU Xiaomin,et al.Energy efficiency analysis of very large scale MU-MIMO downlink systems with transmitting antenna selection[J].Telecommunication Engineering,2014,54(9):1270-1274.(in Chinese)

[3] 张燕,岳殿武. 具有大规模天线选择与功率分配的协作通信[J].电讯技术,2015,55(10):1087-1093. ZHANG Yan,YUE Dianwu.Cooperative communication with massive antenna arrays selections and power allocation[J].Telecommunication Engineering,2015,55(10):1087-1093.(in Chinese)

[4] SANAYEI S,NOSRATINIA A. Antenna selection in MIMO systems[J].IEEE Communications Magazine,2004,42(10):68-73.

[5] GOROKHOV A,COLLADOS M,GORE D,et al.Transmit/receive MIMO antenna subset selection[C]//Proceedings of 2004 IEEE International Conference on Acoustics,Speech,and Signal Processing.Montreal,Que.,Canada:IEEE,2004: 13-16.

[6] NAEEM M,LEE D C. Low-complexity joint transmit and receive antenna selection for MIMO systems[J].Engineering Applications of Artificial Intelligence,2011,24(6):1046-1051.

[7] WANG J,PÉREZ-NEIRA A,GAO M,et al.A concise joint transmit/receive antenna selection algorithm[J].ChinaCommunications 2013,10(3):91-99.

[8] NAEEM M,LEE D C.Near-optimal joint selection of transmit and receive antennas for MIMO systems[C]//Proceedings of 2009 International Symposium on Communications and Information Technology. Icheon,South Korea:IEEE,2009:572-577.

[9] MAKKI B,IDE A,SVENSSON T,et al.A genetic algorithm-based antenna selection approach for large-but-finite MIMO networks[J].IEEE Transactions on Vehicular Technology,2017,(99):1-1.

[10] DONG J,XIE Y,JIANG Y,et al.Particle swarm optimization for joint transmit and receive antenna selection in MIMO systems[C]//Proceedings of 2015 IEEE International Conference on Communication Problem-Solving.Guilin:IEEE,2015:237-240.

[11] 施荣华,谢羽嘉,董健,等. 一种快速的MIMO系统联合收发端天线选择算法[J].中南大学学报(自然科学版),2016(2):482-487. SHI Ronghua,XIE Yujia,DONG Jian,et al.A fast joint transmitting and receiving antenna selection algorithm for MIMO systems[J].Journal of Central South University(Natural science),2016(2):482-487.(in Chinese)

[12] 林毅松.MIMO系统中基于信道容量的收发联合天线选择算法的研究[D].泉州：华侨大学,2015. LIN Yisong.Study on joint transmit and receive antenna selection algorithm based on capacity in MIMO systems[D].Quanzhou:Huaqiao University,2015.(in Chinese)

[13] CHU S C,TSAI P,PAN J S. Cat swarm optimization[J].Lecture Notes in Computer Science,2006(6):854-858.

[14] SHARAFI Y,KHANESAR M A,TESHNEHLAB M.Discrete binary cat swarm optimization algorithm[C]//Proceedings of 2013 3rd International Conference on Computer,Control & Communication. Karachi,Pakistan:IEEE,2013:1-6.

Application of Binary Cat Swarm Optimization inLarge-scale MIMO Antenna Selection

LI Shumei1，ZHUANG Mingjie1，2，ZHUANG Hong2

(1.Engineering Institute,Huaqiao University,Quanzhou 362021,China；2.Fujian Internet of Things Scientific Research Institute，Quanzhou 362000,China)

The antenna selection technique balances the performance and hardware cost in the multiple input multiple output(MIMO) systems,but the complexity issue of the large-scale transmit and receive antenna selection on MIMO system has not been fully solved. According to the criterion of maximizing channel capacity,in this paper,two binary coding strings are used to represent the selected states of the transmitter and receiver antennas respectively,and binary cat swarm optimization(BCSO) is applied to multiple antenna selection. The formula of MIMO channel capacity is used as the fitness value of the cats,then the problem of transmit and receive antenna selection is transformed into the location optimization of the cats.The antenna selection model with BCSO is established and and its implementation steps are given. The simulation results show that,the proposed algorithm has better convergence and lower computational complexity than the method based on matrix simplification and particle swarm optimization(PSO) algorithm,moreover it can get closer to the optimal algorithm in the aspect of channel capacity. The proposed algorithm is very suitable for the MIMO system with a large number of antennas in joint transmit and receive antenna selection.

multiple input multiple output(MIMO);antenna selection；binary cat swarm optimization;channel capacity;particle swarm optimization algorithm

10.3969/j.issn.1001-893x.2017.06.014

李淑梅,庄铭杰，庄弘.二进制猫群算法在大规模MIMO天线选择中的应用[J].电讯技术，2017,57(6):698-702.[LI Shumei，ZHUANG Mingjie，ZHUANG Hong.Application of binary cat swarm optimization in large-scale MIMO antenna selection[J].Telecommunication Engineering,2017,57(6):698-702.]

2017-03-27；

2017-05-16 Received date:2017-03-27；Revised date：2017-05-16

福建省自然基金计划项目(2012J01270);泉州市科技计划重点项目(2012Z82)；华侨大学自然科学基金(11BS430)；2015级华侨大学研究生科研创新能力培养项目(1511322002)

TN919.3

1001-893X(2017)06-0698-05