改进萤火虫算法在Okumura-Hata模型修正中的应用*

2017-06-23刘宝生李章义

电讯技术 2017年6期

关键词：电波萤火虫适应度

刘宝生，潘琳，李章义

(国家无线电监测中心陕西监测站，西安 710200)

改进萤火虫算法在Okumura-Hata模型修正中的应用*

刘宝生，潘琳，李章义**

(国家无线电监测中心陕西监测站，西安 710200)

针对Okumura-Hata模型在不同区域对电波传播衰减的预测与实测难以匹配的问题，提出了一种Okumura-Hata模型修正方法。提取Okumura-Hata模型的各参数作为带约束条件的优化变量，以预测值与实测值的均方根误差和平均误差的加权和构造适应度函数，运用萤火虫算法进行优化实现Okumura-Hata模型在西安市区的本地化。在萤火虫算法中引入了“基因突变”和“优胜劣汰”操作，形成了一种改进型算法。基于大量实测数据的模型修正结果表明，所提方法可使电波损耗的预测值与实测值的均方根误差达到理论最小值9.585 9 dB，具有可行性。与基本萤火虫算法相比，改进的算法全局搜索能力更强，收敛速度更快。

电波传播；Okumura-Hata模型；萤火虫算法；模型修正；全局搜索能力

1 引言

电波传播存在环境建模困难、传播机理复杂等特性，因而应用于微蜂窝的射线追踪法、抛物方程法等方法难以在宏区域发挥有效作用。与之相对，诸如Okumura、Okumura-Hata、Egli、COST231等基于大量实测数据形成的电波传播经验模型有效利用了电波传播统计特性，回避了复杂的微观电波传播计算，成为链路预算的一种有效技术手段。

Okumura-Hata模型是在Okumura[1]和Hata[2]等人基于大量测试数据总结出来的，主要应用于市区路径损耗的预测，与其他常见经验模型相比，用该模型预测的路径损耗与实测值最为接近[3]，因此，该模型得到了广泛关注。文献[4]将模型扩展后应用于郊区场强预测，结果与实测数据误差小于6 dB。文献[5]应用该模型预测了2.4 GHz室外传播损耗，给出了无线局域网(Wireless Local Area Network,WLAN)规划建议。文献[6]运用该模型研究了铁路GSM-R信号的路径衰减特性。文献[7-8]用最小二乘法完成了模型的本地化修正，但是该方法只能优化两个参数，且需要严格的数学求导和矩阵操作，有其局限性。文献[9]用牛顿二阶算法修正模型后，与原模型相比，获得的结果改善了7 dB，但是考虑的传播距离小于2 km，不具有广泛代表性。

本文介绍了Okumura-Hata模型和萤火虫算法的基本原理,重点阐述了场强实测数据的预处理方法、萤火虫算法的改进及适应度函数的构造方法，并给出了应用改进萤火虫算法修正Okumura-Hata模型的具体方法；最后用西安市区VHF频段典型频点的传播衰减预测实例说明本文方法的有效性，并将文中方法与最小二乘法进行了比较，得出了一些有益结论。

2 基本原理

2.1 Okumura-Hata模型

Okumura-Hata模型的基本公式为

L=69.55+26.16lgf-13.82lghte-a(hre)+(44.9-6.55lghte)lgd,

(1)

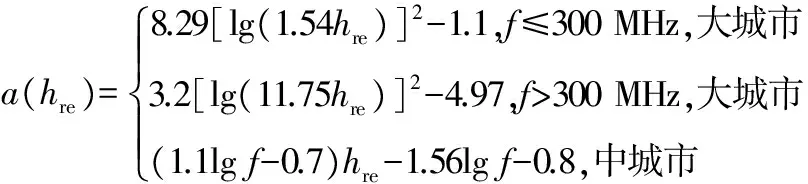
(2)

式中：a(hre)为接收天线高度修正因子；L为中值路径损耗，单位dB；f为频率，范围150～1 500 MHz；hte为天线有效高度，范围30～200 m；hre为接收天线有效高度，范围1～10 m；d为发射站到接收站的距离，范围1～20 km；a(hre)为有效接收天线高度修正因子。

在郊区和农村环境下对应的经验公式为

(3)

2.2 萤火虫算法

萤火虫算法(Firefly Algorithm,FA)[9]是一种高级仿生算法，有研究表明其优化能力比粒子群算法和遗传算法强。该算法源自于对萤火虫群体行为的模拟，基于萤火虫相互吸引的前提，对它们的行为进行抽象：萤火虫的吸引力与发光强度正相关,与它们之间的距离负相关，亮度小的萤火虫向亮度大的萤火虫靠近，最终完成萤火虫的自发式移动和聚集。下面给出该算法的数学描述。

每只萤火虫代表待优化问题的一个可能解,那么使这个“可能解”靠近最优解的过程就是萤火虫的移动过程。假设萤火虫i的亮度随着距离的增大、空气的吸收而减弱，可定义萤火虫i对萤火虫j的相对亮度为

(4)

式中:Ii为萤火虫i的初始光强度;γ为光在空气中的衰减常数，通常取值0.01～100;rij为萤火虫i到萤火虫j的欧式距离,

(5)

式中:D为变量的维数，xi为含D维变量的第i只萤火虫。

由亮度和吸引力成比例的假设，定义萤火虫i对萤火虫j的吸引力为

(6)式中:β0为最大吸引力(r=0时)常数，通常取值为1。

萤火虫j被萤火虫i吸引而更新自己的位置，规则为

xj(t+1)=xj(t)+βij(rij)[xi(t)-xj(t)]+αεj。

(7)

式中:t为算法当前迭代次数;α为扰动常数，取值范围为[0,1];εi是均匀分布的随机数向量。式(7)是算法自动寻优的理论依据。

萤火虫算法已广泛应用于各种工程科学问题，但未见其在电波传播领域的应用报道。

3 Okumura-Hata 模型修正方法

3.1 数据采集及预处理

修正模型之前需要进行信号实测，采集经纬度和对应的场强中值。其中采样点的位置分布特性和稀疏性很大程度上决定了传播模型的修正效果，因此，作者为了降低因数据采集造成的模型修正误差，驱车驶遍西安市区主要道路(如图1所示)对电视塔发射的107.8 MHz调频广播信号进行采集。

图1 实测数据分布

在采集到的15万条数据中，有不少数据是因为监测车所必须进行的调头而在同一路段重复测得的，所以需要剔除，而且行驶过程中遇到红灯或堵车时会出现某一位置重复监测的情况，造成数据堆积，也需要去除，从而确保采集的数据能尽可能反应电波真实的分布情况。

采用以下两个步骤完成上述数据的预处理：

(1)根据采样点经纬度和地球半径，获取采样点间距，判断间距若小于某一设定值，则剔除这些采样点，连续剔除的点间距之和不超过设定值；

(2)计算采样点到信号发射塔的距离，将距离等间距分为M段，每一段内随机选取N个经过第一步筛选后的采样点，则可得到近似均匀分布的实测数据。

3.2 改进的萤火虫算法(Improved Firefly Algorithm，IFA)

仿生优化算法均存在过早收敛现象，萤火虫算法也不例外。为克服这一缺点，在群体中引入变异个体，丰富种群的多样性。具体实施策略如下：

(1)引入变异概率pm，产生一个0～1之间的随机数pr，随机选取一个个体，记为xi，使之作如下变异：

λ=0.5(xbest-xi),

(8)

(9)

式中:xbest为最佳个体;λ为变异步长;xi,new为新个体，仅在pr>pm时随机选择的个体发生变异。

计算xi,new的适应度值，若适应度值好于xi，则该新个体替换旧个体；否则，令种群的最优个体替换最差个体，模拟生物“优胜劣汰”的过程。数学表达式如下：

(10)

式中:F为适应度值，xworst为最差个体。

3.3 Okumura-Hata模型修正方法

在修正Okumura-Hata模型时，需要将式(1)改写成如下形式：

L=k1+k2lgf-k3lghte-k4a(hre)+[k5-k6lghte]lgd。

(11)

对比式(1)和式(11)可以看出，它们的形式完全一样，只是前者是后者的一种特殊情形。

由于Okumura-Hata模型主要由电波频率、收发天线高度和传播距离决定，所以参数k1～k6的变化只会对模型进行调整，而不会使模型发生本质上的改变，这使得运用优化算法进行优化具有可行性。

适应度函数的构造对算法的发挥有决定性的作用，因此本文将评价传播模型优劣的两个重要因素——均方根误差(Root Mean Squared Error,RMSE)和平均误差(Mean Error,ME)进行加权相加后作为适应度函数：

(12)

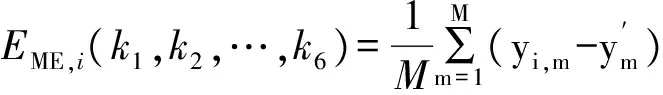
(13)

Fi=ωERMSE,i+(1-ω)EME,i。

(14)

模型修正的主要操作步骤归纳如下：

(1)数据采集并预处理；

(2)设定每个参数的取值区间，随机生成初始种群；

(3)设定算法参数，计算适应度函数值，随机产生选取一个变异个体并执行变异操作，运用萤火虫算法对参数k1～k6进行迭代优化；

(4)随着迭代的进行，判断适应度函数精度或迭代次数是否达到要求，若是则停止优化；否则，继续迭代直到满足停止条件。

算法流程如图2所示。

图2 IFA修正Okumura-Hata模型流程图

4 模型修正及结果分析

基于西安市区107.8 MHz的实测数据，应用上述方法对Okumura-Hata模型进行修正。hte=240 m，hre=1.5 m，f=107.8 MHz。

种群包含10个个体，每个个体由6个优化变量组成，其中每个变量的优化约束区间如表1所示。

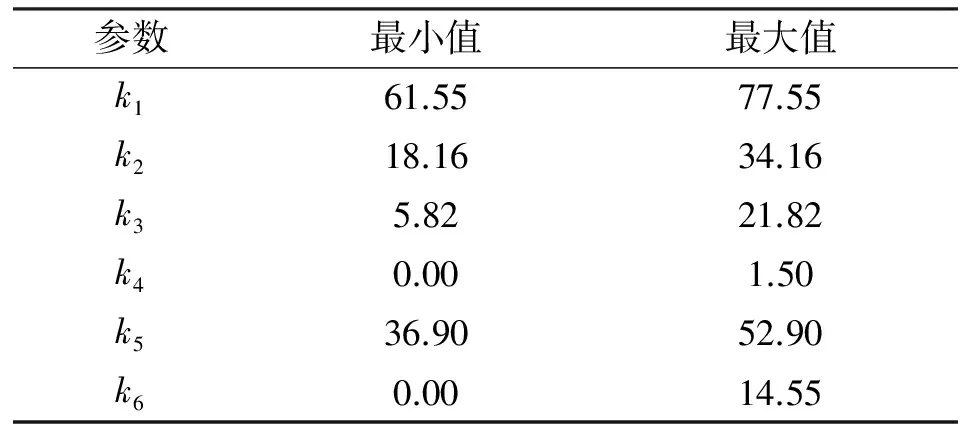
表1 种群取值范围Tab.1 The population range

IFA除增加参数pm外，其他参数与FA设置相同，如表2所示。

表2 参数设置Tab.2 Parameter settings

图3给出了基于本文方法、基于最小二乘法的修正模型以及未修正模型预测的路径损耗曲线，可见修正模型与实测数据达到了很好的匹配，对应的模型参数值如表3所示。

图3 路径损耗预测曲线(实线与点画线几乎重合)

参数原始取值本文方法最小二乘k169．5567．0064．58k226．1627．5326．16k313．8216．0113．82k41．000．441．00k544．942．0741．46k66．556．816．55

为了比较IFA与FA的优化能力，将两者各独立运行20次，平均最佳适应度值随迭代次数的变化如图4所示，可见IFA与FA在迭代不到20次时均已趋于收敛，而IFA收敛到的适应度函数值好于FA，说明IFA的全局寻优能力较强。

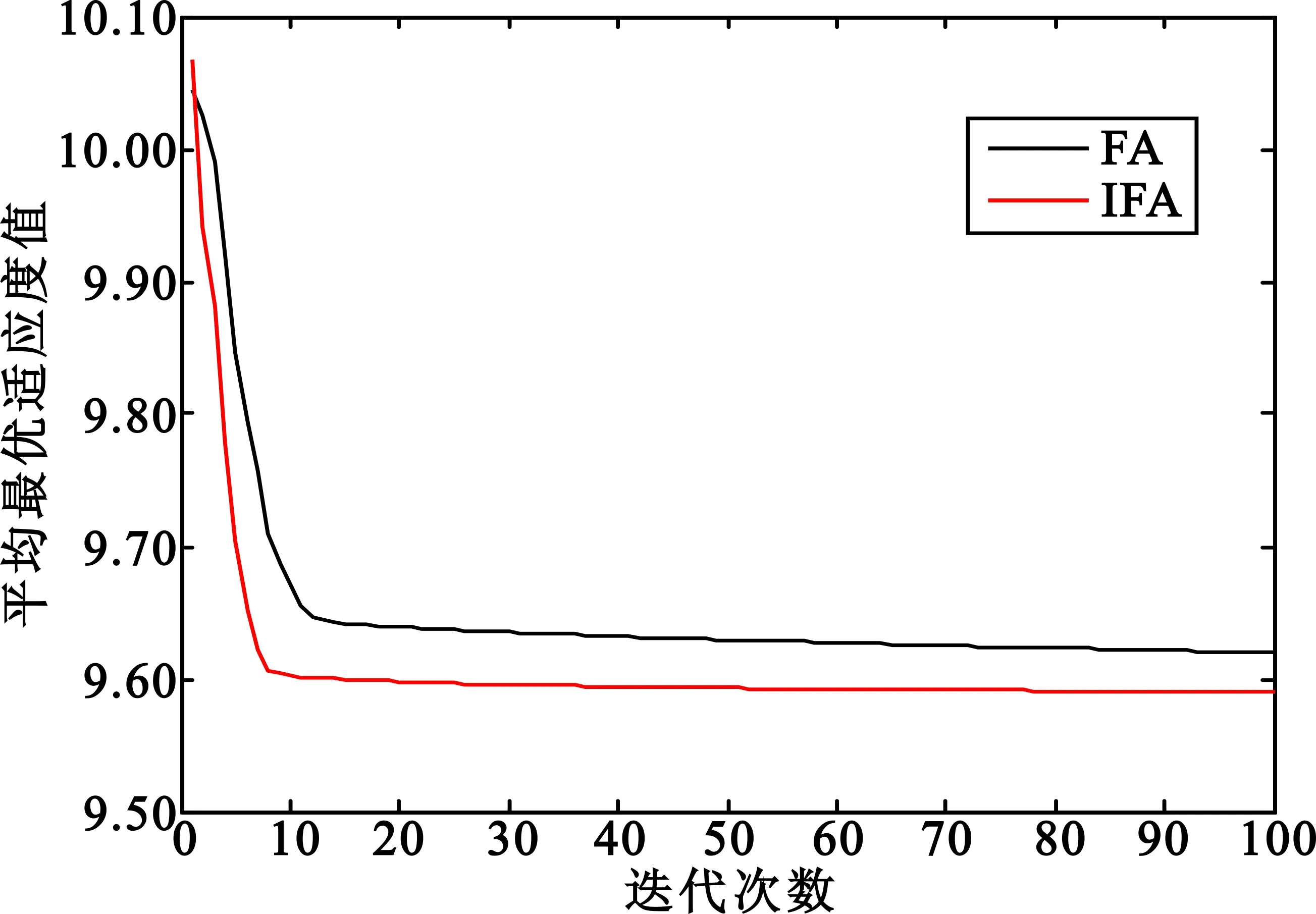
图4 FA与IFA迭代曲线

图5是FA和IFA 20次仿真结果分布，可见IFA优化结果起伏较小，有较强的鲁棒性。

图5 FA和IFA 20次优化结果分布

表4所示是FA、IFA以及最小二乘法计算结果统计(其中最小二乘法和原模型的均方根误差恒定)，可以看出，FA、IFA都达到了9.585 9 dB的理论最小均方根误差，而IFA的平均值和最大值都好于FA，证明了改进算法的有效性。

表4 误差统计Tab.4 Error statistics

5 结束语

为寻找适合西安市VHF频段的Okumura-Hata修正模型，作者针对该频段中间频点的广播电台(107.8 MHz)场强进行全市区高密度采样，对数据进行等间隔、分段提取后，应用最小二乘法、萤火虫算法及其改进方法优化修正了Okumura-Hata模型，完成了该模型的本地化,对比得出了以下结论：

(1)采用FA及IFA修正的模型均可使电波路径损耗的预测值与实测值的均方根误差达到理论最小值，方法有较好的可行性。模型的修正是基于西安市区大量实测数据进行的，在类似规模的城市中，该模型具有较大的参考价值。

(2)IFA的收敛速度、全局寻优能力、算法鲁棒性都强于FA。

(3)本文方法可以修正模型的任意参数，并且优化结果不唯一，可限制参数在预期的范围内变动，与最小二乘法相比，具有较高的使用灵活性。

下一步将针对Okumura-Hata模型难以反映局部电磁覆盖特性的情况进行研究，探索多种模型有效结合的手段，为即将到来的5G时代提供更为可靠的通信链路预算方法。

[1] OKUMURA Y,OHMORI E,KAWANO T,et al.Fieldstrength and its variability in VHF and UHF land mobile radio service[J].Review of the Electrical Communications Laboratories,1968,16(9-10):825.

[2] HATA M. Empirical formula for propagation loss in land mobile radio services[J].IEEE Transactions on Vehicular Technology,1980,29(3):317-325.

[3] ROSLEE M B,KWAN K F. Optimization of Hata propagation prediction model in suburban area in Malaysia[J].PIER C,2010(2):91-106.

[4] EKKA A. Pathloss determination using Okumura-Hata model for Rourkela[D].Rourkela,India:National Institute of Technology,2012.

[5] 侯群,高立. 无线局域网室外覆盖路径损耗计算分析及规划布局建议[J].电讯技术,2011,51(8):101-104.HOU Qun,GAO Li.Calculation of WLAN outdoor coverage path loss and system deployment suggestion[J].Telecommunication Engineering,2011,51(8):101-104.(in Chinese)

[6] COTA N,SERRADOR A,VIEIRA P,et al.On the use of Okumura-Hata propagation model on railway communications[J].Wireless Personal Communications,2014,6983(6):1-12.

[7] YANG M,SHI W. A linear least square method of propagation model tuning for 3G radio network planning[C]//Proceedings of the 4th International Conference on Natural Computation. Jinan:IEEE,2008:150-154.

[8] ADEYEMO Z K,OGUNREMI O K,OJEDOKUN I A. Optimization of Okumura-Hata model for long term evolution network deployment in Lagos,Nigeria[J].International Journal on Communications Antenna and Propagation,2016,6(3):146-150.

[9] DJOMADJI D,EMMANUEL T. Optimization of Okumura Hata Model in 800MHz based on Newton Second Order algorithm. Case of Yaoundé,Cameroon[J].IOSR Journal of Electrical and Electronics Engineering,2015,10(2):16-24.

Application of Improved Firefly Algorithm inOkumura-Hata Model Updating

LIU Baosheng,PAN Lin,LI Zhangyi

(Shaanxi Monitoring Station,The State Radio Monitoring Center,Xi′an 710200,China)

To solve the problem that the Okumura-Hata model is not suitable for any area,a new approach for modifying Okumura-Hata model is proposed.The approach extracts Okumura - Hata model’s parameters as the optimization variables with constraint conditions,and constructs fitness function using the root mean square error(RMSE) and the mean error(ME) between predicted values and measured values. Then,the new parameters of Okumura - Hata model will get after the model is optimized by Firefly algorithm. Besides,an improved Firefly algorithm based on “gene mutation” and “law of survival of the fittest” is proposed. The simulation results show that the RMSE of the updated model can approach the theoretical minimum limit 9.585 9 dB. Compared with the basic Firefly algorithm,the improved one has a stronger global searching ability and a faster convergence speed.

electromagnetic wave propagation;Okumura-Hata model;firefly algorithm;model updating;global search ability

10.3969/j.issn.1001-893x.2017.06.008

刘宝生，潘琳，李章义.改进萤火虫算法在Okumura-Hata模型修正中的应用[J].电讯技术，2017,57(6):661-665.[LIU Baosheng,PAN Lin,LI Zhangyi.Application of improved firefly algorithm in Okumura-Hata model updating[J].Telecommunication Engineering,2017,57(6):661-665.]

2017-01-04；

2017-02-28 Received date:2017-01-04；Revised date：2017-02-28

国家自然科学基金重点资助项目(61631015)

TN011

1001-893X(2017)06-0661-05