一定规模电动汽车集群充电优化策略研究
2017-06-23冯明,熊炜
冯 明,熊 炜
(贵州大学 电气工程学院,贵州 贵阳 550025)
一定规模电动汽车集群充电优化策略研究
冯 明,熊 炜
(贵州大学 电气工程学院,贵州 贵阳 550025)
电动汽车规模化应用后,研究电动汽车的充电优化策略,不仅可以提高电动汽车充电效率,还能起到削峰填谷的作用。以某一固定时段内一定规模电动汽车进行集中充电的模式为研究对象,首先研究了电动汽车充电时长随机规律,其次在峰谷电价的基础上,建立了以用户总费用及单桩最大充电时间最小为目标的电动汽车集群充电策略优化模型,最后采用改进遗传算法进行求解,并与无序充电进行比较,验证了所提方法的可行性和有效性。
电动汽车;充电时长;有序充电策略;遗传算法
0 引言
随着电动汽车的快速发展[1-2],电动汽车的无序充电将对城市配电网规划及安全稳定运行产生较大影响。
针对电动汽车的无序充电对电网产生的影响,专家学者开展了以下研究:电动汽车充电负荷建模与仿真计算、电动汽车接入对电力系统的影响、电动汽车的充放电控制与利用等[3]。文献[4-6]根据统计数据,对电动汽车起始充电时间和日行驶里程概率分布分析,采用蒙特卡洛模拟与概率统计分析结合的方法,建立了电动汽车充电负荷概率模型。文献[7]考虑了充电时长差异、充电能力限制等因素对电动汽车充电负荷的影响。文献[8]中讨论了电动汽车的V2G特性,不仅可以作为负荷吸收电能,还可通过放电向电网输送电能。文献[9]在电动汽车V2G特性基础下,在考虑峰谷电价的基础上,对各类电动汽车的充放电利用来降低用户费用及配网损耗。文献[10]以平抑负荷波动,减小负荷峰谷差,避免充电过程产生新的负荷高峰,作为确定电动汽车充电开始时间,但是会以一部分用户的充电要求得不到满足作为代价。文献[11]基于电网分时电价特征,以配电变压器容量及最大限度满足用户充电需求为约束条件,以充电站运营收益最大化为目标,建立了充电站内电动汽车有序充电的数学模型,对于短时间电能需求大的用户满意度较低。以上对电动汽车有序充电研究中,侧重于通过电动汽车充电顺序的控制来满足电网的安全稳定、充电站运营收益,会以牺牲一部分用户得不到充电服务作为代价。
不同类型电动汽车,如公交车、公务车、出租车、私家车等的出行规律和充电需求各异,具有较强的随机性。根据各自的自身运行特点及不同的充电模式,如公交车、公务车、大型停车场私家车均可在夜间采用集中充电模式,从而具有调度可行性。本文计及充电设施配置比例的影响,研究一定规模电动汽车集群充电优化策略,兼顾用户和电网的利益,以集群充电站充电完成时间(单桩最大充电时长)及充电总费用最小作为优化目标,提高充电效率,减少用户费用,同时起到平滑负荷、改善电能质量等作用。
1 电动汽车充电时长
1.1 电动汽车充电模式
目前电动汽车主要的充电模式分为慢速充电、快速充电和电池更换三类。慢速充电模式充电时间较长,适用于具备充电功能的大型停车场、居民小区等。快速充电方式主要用于高速公路上、超市、医院等,主要对象是应急充电和中长途旅行的客户。更换电池充电模式可以快速完成电池的加满,多用于公共场合电动汽车的电能补给[12]。
文中电动汽车均采用慢速充电方式。
1.2 行驶里程
现有电动汽车行驶数据不足以反映普遍的规律性,而电动汽车运行规律主要是由用户自身的出行需求决定的。假设电动汽车的使用不改变用户的行驶特性,因此在分析中使用燃油汽车的相关运行规律代替电动汽车的运行规律。
根据文献[13-14]中美国交通部对全美家用车辆调查的统计结果,对统计数据进行归一化处理后,用极大似然估计的方法,日行驶里程近似服从对数正态分布,其概率密度函数为:
(1)
式中:μd=3.68;σd=0.88;x为日行驶里程,km。
1.3 充电时长
电动汽车能耗、电池容量的差异性,使得行驶同一里程后电动汽车蓄电池的荷电状态存在差异性[11];电动汽车日行驶里程取决于用户的出行习惯和行驶特性,具有随机性特点;不同种类电动汽车采用的蓄电池可能不同,充电特性也存在差异,这些因素都会导致电动汽车充电时长的不确定性。
本文以同一类电动汽车为研究对象,忽略能耗差异性对充电时间的影响。假设电动汽车行驶同样路程消耗能量一样,在充电功率一定下,行驶里程与充电时长成正比例关系,充电时长与日行驶里程关系式如下:

(2)
式中:tcr为充电时长,h;x为日行驶里程,km;w为百公里耗电量,kW·h;Pc为充电功率,kW;η为充电效率。
2 电动汽车集群充电策略数学模型
2.1 问题描述
公交车、公务车等有很强的运行规律,有明确的停运及运营时间,私家车在下班时间集中入库,以上类型电动汽车具有在某时间段内停止行驶,方便对其进行集中充电的特点,本文研究的问题就是如何对这类电动汽车集中有序充电策略进行优化,使得所有电动汽车完成充电时充电时长最大桩充电时间最小及考虑峰谷电价不同的用户充电总费用最小。考虑到在同一台充电设施充电的一组电动汽车,组内充电次序变化时,不影响该组电动汽车充电完成时间,因此充电优化只需通过确定每台电动汽车的充电设施的选择,来优化总充电时长。
另外,若采用更换电池充电模式,可将电池类比上述电动汽车,可以通过上述优化目标优化每块电池的充电。
2.2 数学模型
2.2.1 假设条件
设充电站充电设施台数为N,在T时刻之前,所有电动汽车进入充电站,进入充电站的电动汽车辆数为M(M>N)。
假设条件如下:
(1)在T时刻之前,所有电动汽车都已经进入充电站,等待充电。
(2)所有电动汽车充满电作为充电结束时间。
(3)电动汽车以恒功率充电。
(4)每台电动汽车只能选择一台充电设施充电,充电完成前不允许更换充电设施。
(5)每台充电设施在同一时刻只能对一辆电动汽车充电。
2.2.2 目标函数
本文以用户充电总费用最低及单桩最大充电时间最小作为目标,目标函数表达式如下:
minF=F1(X)+F2(X)
(3)
式中:F1(X)为集群充电中单桩最大充电时间对应的充电费用;F2(X)为用户充电总费用,计算公式如下:
(4)
式中:X为N×M矩阵,为待求问题的解;xi(i=1,2,…,M)为n维列向量,用来表示编号为i的电动汽车所选择的充电设施;Tev为M维列向量,ti(i=1,2,…,m)为Tev中元素,代表编号为i的电动汽车充满电的充电时长;Pc为充电功率;α1为谷时电价;α2为峰时电价;T0为谷时段时间长度。
2.2.3 约束条件
(1)变量逻辑约束
每辆电动汽车只能选择一个充电设施充电,充电完成前不允许更换充电设施。一个充电桩每个时刻只能给一辆电动汽车充电,每个充电桩至少给一辆电动汽车提供充电。xi(i=1,2,…,M)即元素i所在列的列标代表该电动汽车所选择充电设施编号:
(5)
r(x1,x2,…,xM)=min(M,N)
(6)
若充电桩数目N=3,电动汽车数目为M=5,则x2=(0,0,1)T表示编号为2的电动气车在3号充电桩充电。
(2)电动汽车与充电设施数量关系约束
M>N
(7)
式中:M为电动汽车数量;N为充电设施数量。
(3)充电功率约束
Pc=P0
(8)
式中:Pc为充电桩充电功率,即恒定功率充电。
(4)电动汽车充电时长约束
电动汽车充电最小时长由用户出行时期望的电池荷电状态决定,电动汽车充电最大时长由用户最大续航里程决定,用户电动汽车充电时长满足下面约束:
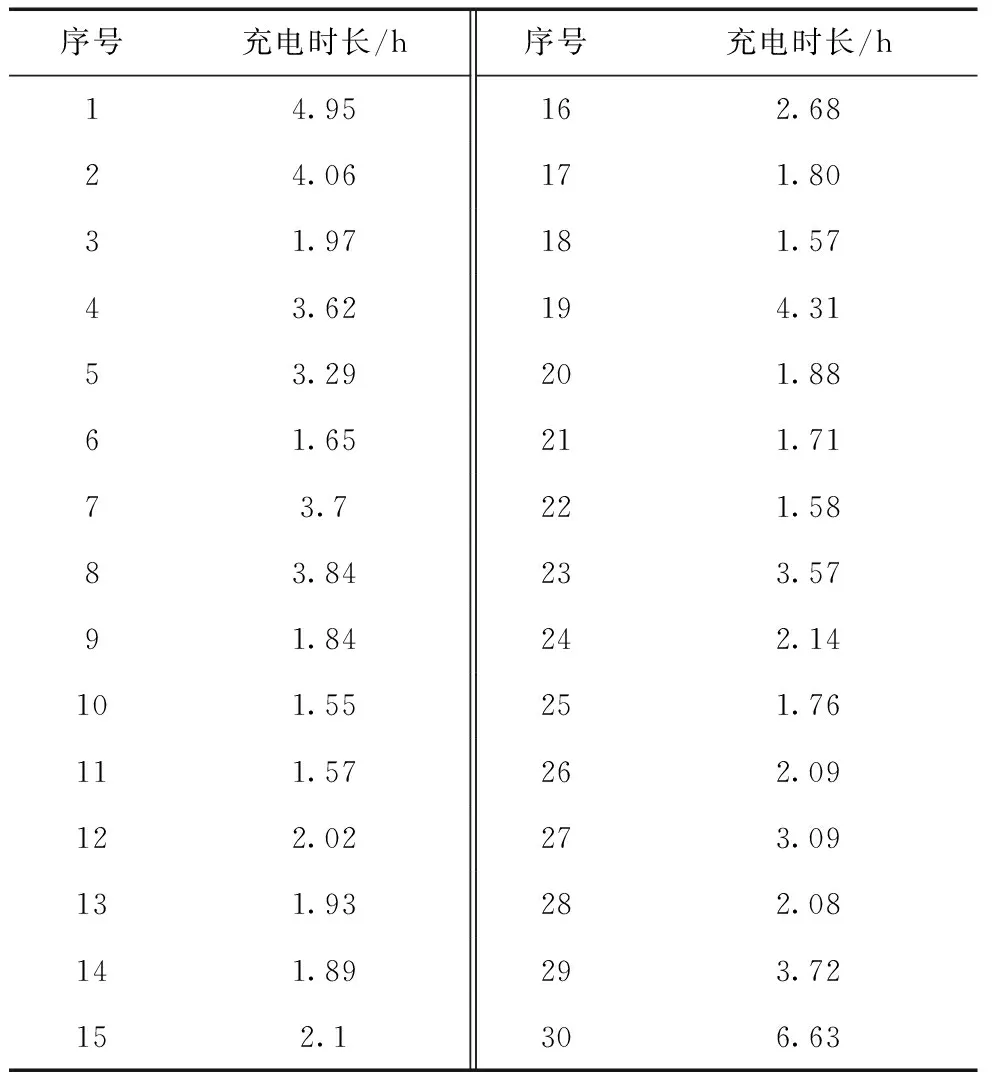
tmin (9) (5)桩充电时长约束 避免上一次集群充电对下一次集群充电的影响,桩充电时长约束满足: 0 (10) 2.3 充电流程 电动汽车进入充电站后,由于充电桩数目小于车数量,同时充电桩每个时刻只对一辆电动汽车充电,其充电流程如下: (1)电动汽车用户进站后,对电动汽车进行编号,并通过剩余电量计算其充电需求时间。 (2)根据电动汽车的充电时长进行有序充电优化,得出一定规模电动汽车充电优化法方案,对应编号电动汽车所选择的充带电设施编号,选择同一个充电设施充电的电动汽车作为一组。 (3)工作人员将电动汽车开到各自所需选择的充电设施区域,并对各组电动汽车在各自充电设施先后依次充电即可。 遗传算法是模仿生物遗传与进化原理的一种自适应概率优化方法。它通过基因(变量)的组合编码来描述优化问题的解(个体),可方便地处理离散变量。它根据适应度值的大小来决定个体的性能,并通过优胜劣汰的原则来进行种群的遗传进化,具体的遗传操作包括选择、交叉和变异算子。 本文采取二进制编码,对X进行编码,X由M个N维列向量组成,可以看成多决策量,每一个列向量xi都可以看成一个决策量,xi是N维向量且其中元素组成只有0,1,可以直接作为遗传编码,本文考虑到xi的特点,对其改进可以缩短编码长度。具体编码过程如下: xi是一列向量,且其中只有一个元素为1,将其转换zi(zi为正整数),zi满足下式: xi(zi)=1 (1≤zi≤N) (11) 式中:zi为xi列向量中元素为1的列标,zi值反应编号为i电动汽车的选择的充电设施的编号。 zi是一正整数,xi取值范围都一样,所以xi的二进制编码位数一样长,此处首先确定二进制编码的位数l,取决于充电桩数目N,l与N之间的关系满足如下: 2l-1 (l,N均为正整数) (12) 对zi进行二进制编码为: zi→ai1ai2…ail,aij∈{0,1} (j=1,2,…,l) Z的二进制编码 Z=(z1,z2,…,zm) Z→a11a12…a1la21a22…a2l…am1am2…aml 其中 aij∈{0,1},i=1,2,…,m; j=1,2,…,l 对X的整个编码过程如下: X→Z→a11a12…a1la21a22…a2l…am1am2…aml 上述编码中aij值根据文献[15]中介绍的谢菲尔德大学遗传算法工具箱确定。 其他步骤与一般遗传算法步骤一致,在此不再赘述。 本文遗传算法计算流程如图1所示。 图1 基于改进遗传算法电动汽车集群充电计算流程 充电设施数目N取8,电动汽车数目M取30,充电效率η取0.9,百公里耗电量w取15kW·h,Pc取4.5kW。设该充电站所处地电力负荷谷时段为22时至次日8时,即谷时段时间T0为10h,谷时电价以0.3元/°,其他时刻以2元/°计。电动汽车集群充电开始时间为22时,电动汽车的充电时长采取蒙特卡洛模拟仿真的处理,根据日行驶里程概率分布抽取30辆汽车的日行驶里程,在本文中假设下,根据式(2)计算各车充电时长,以此作为本文充电时长计算的样本。几类典型电动汽车续航里程如表1所示[16]。 表1 几类典型电动汽车续航里程 从表中可看出电动汽车续航里程在130~300 km之间,本文以200 km作为电动汽车的续航里程,假设电动汽车用户出行时希望电池蓄电池荷电状态SOC不低于80%,则电动汽车进入充电站后电池蓄电池荷电状态SOC低于80%就有充电需求,因此本文抽取行驶里程为40~200 km之间的数据作为计算样品,由式(4)可知,在M=8时,l=3,即每一个xi用3位二进制编码,从而X二进制编码长度为90。遗传参数设置如表2所示。 表2 遗传算法参数设置 根据行驶里程随机抽取并计算得到的充电时长数据如表3所示。 表3 电动汽车充电时长数据 遗传算法和无序充电结果比较如下: 无序充电是指电动汽车满足上文约束条件随机分配到充电站中的充电桩上充电。电动汽车充电分配如表4所示。 由上述充电结果,得到集群充电单桩最大充电时长及用户充电总费用如表5所示。 从上述结果看,采用遗传算法优化后,与无序充电场景比较,充电时长最大桩充电时间减少了9.55 h,费用减少了117.20元,集群充电费用降低了49.90%。从桩充电时长方差,可看出遗传算法优化后的方差远小于无序充电下方差,即本文所采用的方法,使得各个充电桩充电时长互相接近,从而使单桩最大充电时长减少,同时使更多电动汽车的充电过程在负荷低谷时段进行,低谷时段的电价低,使得用户充电总费用降低。 表4 电动汽车充电分配及对应桩充电时长 表5 遗传算法和无序充电优化结果比较 电动汽车行驶里程的随机性,导致每台电动汽车充电时长的差异性,本文在电动汽车充电时长的分析基础上,建立了一定规模电动汽车集群充电优化模型,采用遗传算法求解。当充电设施有限时,与无序充电场景对比,本文所采用的方法能够使得电动汽车集群充分利用负荷低谷时段完成充电,对电网起到削峰填谷作用,进一步减少用户充电费用。 本文是对同一类型电动汽车全部进站后,对电动汽车集群充电策略优化进行研究。在电动汽车发展初期,电动汽车进站时间相对集中,但未来随着电动汽车规模增长,需计及不同类型电动汽车、电动汽车进站时间对集群充电时长的影响,以便提高充电设施利用率,进一步缩短充电完成时间。 [1] 肖湘宁,温剑锋,陶顺,等.电动汽车充电基础设施规划中若干关键问题的研究与建议[J].电工技术学报,2014,29(8):1-10. [2] 中华人民共和国国务院.国务院关于印发节能与新能源汽车产业发展规(2012~2020年)的通知[EB/OL]. http://www.gov.cn/zwgk/2012-07/09/content_2179032.htm,2012-07-09. [3] 胡泽春,宋永华,徐智威,等.电动汽车接入电网的影响与利用[J].中国电机工程学报,2012, 32(4):1-10. [4] 刘青,戚中译.基于蒙特卡洛法的电动汽车负荷预测建模[J].电力科学与工程,2014,30(10): 14-19. [5] 艾学勇,顾洁,解大,等.电动汽车日充电曲线预测方法[J].电力系统及其自动化学报,2013, 25(6):25-30. [6] 杨波,陈卫,文明浩,等.电动汽车充电站的概率负荷建模[J].电力系统自动化,2014,38(16):67-73. [7] 杨少兵,吴命利,姜久春,等.电动汽车充电站负荷建模方法[J].电网技术,2013, 37(5):1190-1195. [8] 艾圣芳,林湘宁,万云飞,等.考虑V2G模式的含多个电动汽车充电站有源配电网规划研究[J]. 中国电机工程学报,2013,33(34):122-129. [9] 高亚静,吕孟扩,王球,等.计及网损与电动汽车车主利益的分时电价研究[J].电力科学与工程,2014,30(7):37-42. [10] 李秋硕,肖湘宁,郭静,等.电动汽车有序充电方法研究[J].电网技术, 2012, 36(12):32-38. [11] 徐智威,胡泽春,宋永华,等.充电站内电动汽车有序充电策略[J].电力系统自动化,2012, 36(11):38-43. [12] 屠影.电动汽车充电模式及其负荷特性分析[D].南京:南京理工大学,2013:7-9. [13] VYAS A,SANTINI D.Use of national surveys for estimating ‘full’ PHEV potential for oil use reduction[EB/OL].http://www.transpotation.anl.gov/pdfs/HV/525.pdf,2008-07-21. [14] TAYLOR J,MAITRA A,ALEXANDER M,et al. Evaluation of the impact of plug-in electric vehicle loading on distribution system operations[C]// IEEE Power & Energy Society General Meeting, 2009:1-6. [15] 史峰,王辉,郁磊,等.MATLAB智能算法30个案例分析[M].北京:北京航空航天大学出版社,2011:3-16. [16] 杨冰,王丽芳,廖承林,等.不确定充电习惯对电动汽车充电负荷需求及充电负荷调节的影响[J].电工技术学报,2015,30(4):226-232. An Optimal Charging Strategy of Electric Vehicle Aggregated in a Certain Scale FENG Ming, XIONG Wei (College of Electrical Engineering, GuiZhouUniversity,Guiyang 550025,China) With wide application of electric vehicles, the optimal charging strategy for electric vehicles can not only improve the electric vehicle charging efficiency, but also shift peak load. This paper focuses on the centralized charging mode of electric vehicles aggregated in a certain scale during a fixed period of time. Firstly the stochastic characteristics of the electric vehicle charging time are studied, and an optimal charging strategy for aggregated electric vehicle deeming minimum total user cost and minimum of maximum charging time for a single charging pile as its objectives, is presented considering peak-valley electricity price. Then, the problem is solved by the improved genetic algorithm. The results are compared with the ones of random charging case. Finally, the feasibility and effectiveness of the proposed method are verified with the obtained results. electric vehicle(EV);charging time; strategy of coordinated charging; genetic algorithm 常学佳(1990-),男,硕士研究生,主要从事电力系统输电断面方面的研究。 10.3969/j.ISSN.1672-0792.2017.05.006 2016-12-08。 TM727.2 A 1672-0792(2017)05-0029-063 改进遗传算法求解
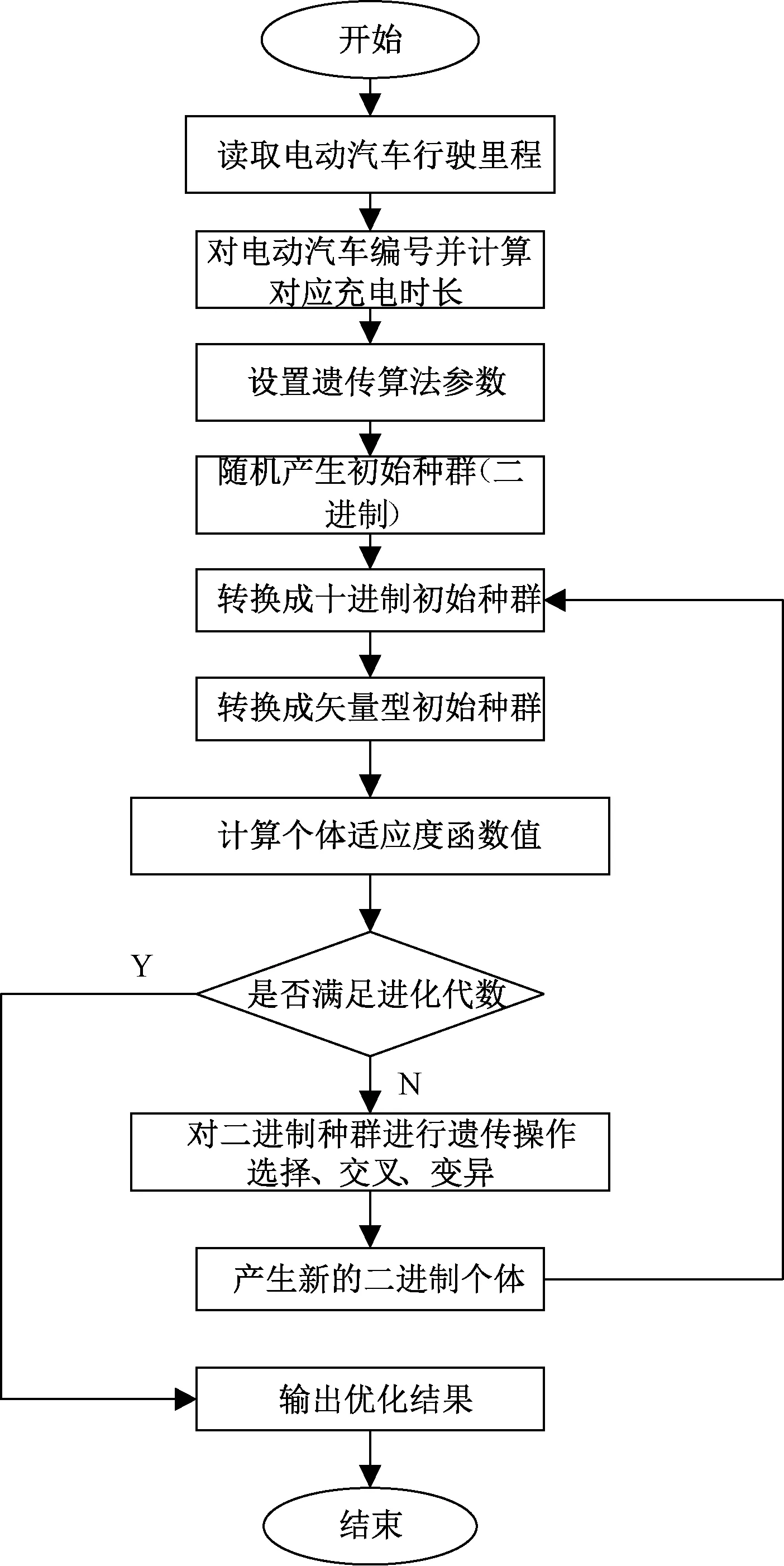
4 算例


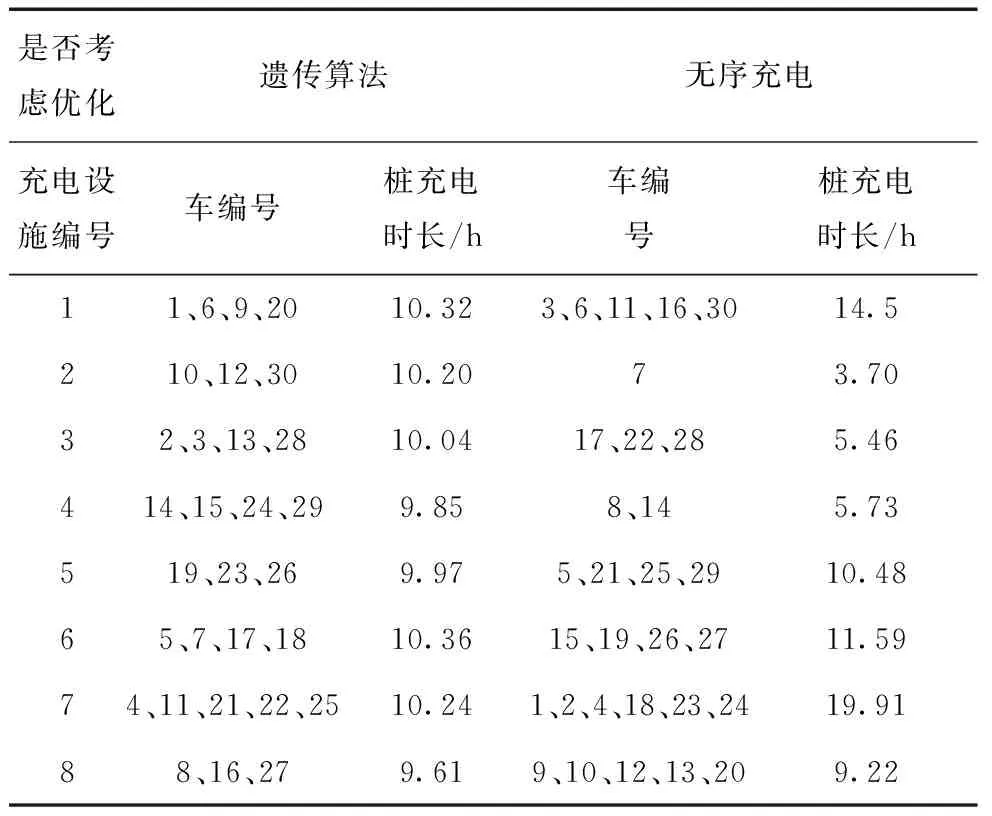

5 结论
