基于MRAS的改进型转速估计法

刘 建,赵华东,王俊鹏，王若羽，辛双志

(山东科技大学 电气与自动化工程学院，山东 青岛 266590)

基于MRAS的改进型转速估计法

刘 建,赵华东,王俊鹏，王若羽，辛双志

(山东科技大学 电气与自动化工程学院，山东 青岛 266590)

针对传统的MRAS转速估计在低速范围内误差较大，不能实现转速精确跟随问题，采用电流模型经过PI运算补偿电压模型，并改进电压型模块，对反电动势的直流部分产生的误差由励磁电流计算而来的转子磁链滤波信号补偿；交变部分，采用饱和反馈进行补偿，以观测到的转子磁链做输入，经过限幅后反馈，补偿转子磁链以降低相位和幅度失真。另外考虑电磁转矩误差，两者并行估计反馈。通过MATLAB/SIMULINK验证此方法能有效减小低速范围内的转速估计误差，实现转速精确跟随，并具有更强的鲁棒性。

MRAS；转速估计；鲁棒性

0 引 言

在实现异步电机高性能调速控制中，除了需要磁链观测外，还需要准确的转速信息，速度闭环是实现高性能调速中必不可少的。传统的控制方法是利用速度编码器，检测出实际转速，响应快、精度高、性能好，能够在低速和零速的情况下平稳运行。不过，速度编码器的引入增加了硬件设备，系统成本也随之增加，并且受检测干扰和硬件故障因素影响，系统的可靠性也降低。因此，研究无速度传感器控制技术具有实际意义[1]。

目前模型参考自适应法可以保证系统的稳定性，且对参数变化有很好的鲁棒性，但在低速时电机参数变化造成低速估计不准，直接影响着系统工作，精度很难保证。采用磁链开环转差型矢量控制，通过稳态转差频率公式，利用磁链和转矩给定信号确定磁场定向进而控制电机[2,3]，精度仍然不够。针对这一问题，很多学者做了研究和改进。部分文献采用一阶惯性环节取代电压模型中的纯积分器之后通过参考磁链矢量经过低通滤波后的矢量予以准确补偿。文献[4]对电压模型改进，利用高通滤波器过滤直流偏差等，最后通过补偿装置进行补偿相位误差。文献[5]在定子坐标系下以定子测变量为状态变量的转速估计，减小了系统直流偏置误差和初始值误差。文献[6]将两相静止坐标系下的电流模型和改进的电压模型转换到两相旋转坐标系，通过Popov超稳定理论，在稳定的系统下推导出转速辨识的算法来估计转速。文献[7]针对PMSM抗干扰性能，通过模糊自整定PI控制器的速度外环实时检测电机转速的变化，并在模糊控制器中输入转速的误差及误差的导数，在线调整PI控制器中的参数从而增强自适应能力。文献[8]对在电压模型中用滞后环节取代纯积分的环节，对转子磁链同样加滞后环节提供补偿。文献[9]针对仿真中积分误差和定子电阻，提出了电流模型补偿电压模型带转速估算方法，使得高速、低速两种情况均能估计转速。但是在频率在截止频率附近时，产生的幅度和相位偏差会严重影响磁链估计的准确性。本文综合以上方法，不仅改进电压模型，也对考虑电磁转矩误差，并行估计并进行反馈，通过仿真验证该方法能有效的减小低速范围内的转速估计误差，具有更强的鲁棒性。

1 传统MRAS转速估计

三相交流异步电机是具有多个变量的复杂控制系统，依据矢量控制原理，将该交流电机控制模型通过坐标转换成直流电机控制模型，从而对控制模型实现解耦，简化控制。在两相静止坐标系下，由电压方程和磁链方程[4]计算可得：

转子磁链电流分量表达式为：

(1)

(2)

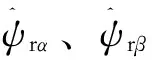
转子磁链电压关系式为：

(3)

(4)

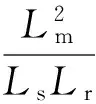
传统的MRAS转速推算法是将电压模型输出结果结合电流模型输出结果，进而利用自适应结构减小估算的转速与实际转速的差距。原理如图1所示。

图1 MRAS转速推算

采用MRAS，在电压模型中没有ω变量，在电流模型有ω变量，所以用电压模型输出值x和电流模型输出值y分别作为预计结果和推算结果，两者结合，计算电动机转速ωr，结果如下：

(5)

2 改进型MRAS转速估计

在低速时，电流模型也起到重要作用，因此对电流模型输出的转子磁链进行PI调节，补偿电压模型估计的转子磁链[9]。由于传统MRAS转速估计包含纯积分环节，容易造成误差累积和直流漂移尤其在低速范围，误差明显变大，转速估计模块不足以替代速度编码器，因此取消纯积分环节采用一阶惯性环节。因为在频率接近或低于截止频率时,所产生的幅度和相位偏差会严重影响磁链估计的精确性，所以对反电动势误差所引起的偏差采用补偿措施。

反电动势误差由直流部分和交变部分组成。针对直流部分，由励磁电流计算而来的转子磁链滤波信号补偿。针对交变部分，采用饱和反馈进行补偿，以降低相位和幅度失真，饱和反馈以观测到的转子磁链做输入，经过限幅，完成对转子磁链的补偿[10]。

传统MRAS电压模型下，转子磁链为：

(6)

转子反电动势为:

(7)

改进后的一阶惯性环节为：

er·Tc/(1+Tcp)

加上转子磁链补偿后即为改进后模型。改进后模型如图2所示。

图2 改进电压型模块

电流模型作为推算值，公式为：

(8)

另外，将考虑电磁转矩误差，得到更加准确的转速估计值。

电磁转矩方程：

(9)

电磁转矩估计方程：

(10)

运动方程：

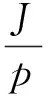
(11)

式中：J为转动惯量，kg·cm2；ωr为实际转速，r/min。

以估计值方式表示为：

(12)

电磁转矩误差为：

(13)

改进的电压模型和电流模型估计的转子磁链误差经过PI调节后的值组成回路，并行考虑[11]。

改进后具体结构框图如图3所示。

图3 改进转速估计结构框图

3 基于改进型MRAS转速估计模型的仿真与分析

为了验证改进型MRAS转速估计的准确性，分别对传统MRAS转速估计和改进型MRAS转速估计进行仿真验证与比较。系统仿真结构图如图4所示。

电机三相定子电压与电流经过Clark变换得到在静止坐标系下的两相电压和电流，两相静止坐标系下的电流经过Park变换得到两相旋转坐标系下电流。其与两相静止坐标系电压通过转子磁链和转速估计模块计算出的ωr和同步旋转角度θ。接下来对旋转坐标系下的电压进行补偿。经过Park变换得到两相旋转坐标下的定子电流，采用 PI 闭环控制得到解耦后的定子电压变量，Park反变换后得到两相静止坐标下的电压，最后经SVPWM调制后控制逆变器[12]。

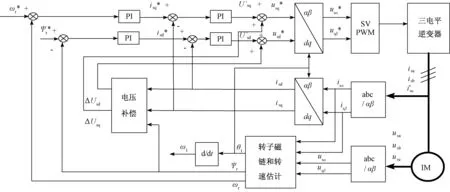
图4 无速度传感器系统仿真结构图

实验用到的参数设置如表1所示。

仿真中设定电机转速在[0 0.4 0.7]s时为 [0 100 -100]r/min。电机空载启动。在时间为[0 0.2 0.8 ]s时，施加负载[0 40 60 ]N·m。对于改进的转速估计模型，检测到的实际转速和估计转速对比如图5所示。

图中：1为比较平滑曲线表示检测到的实际转速；2为相对波动的曲线表示估计转速。

对于电机施加的转矩波形如图6所示。

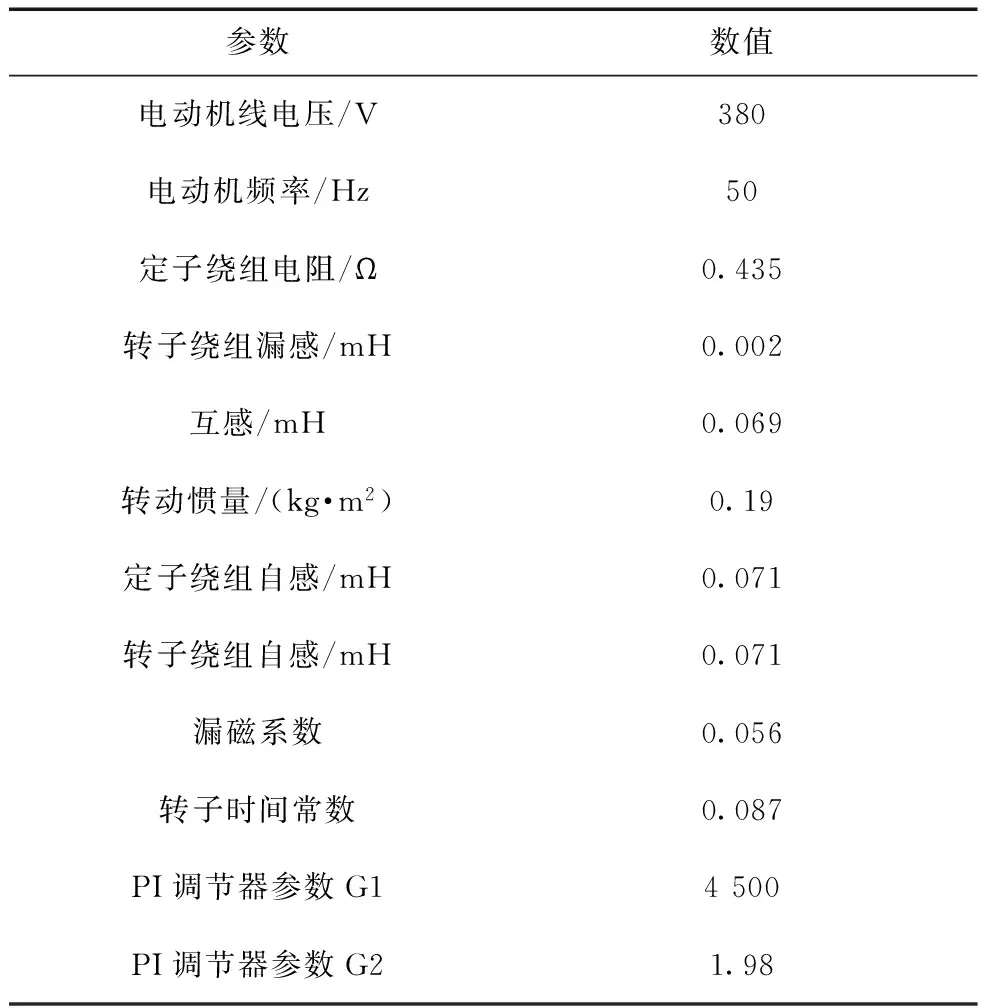
表1 参数设置

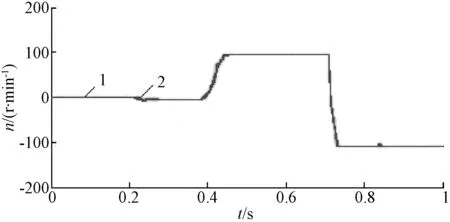
图5 实际转速与估算转速对比图

图6 负载转矩波形图

实际转速和估计转速之差的波形如图7所示。

图7 实际转速与估算转速误差波形图

传统的电压型转速估计，实际转速和估计转速对比波形如图8所示。

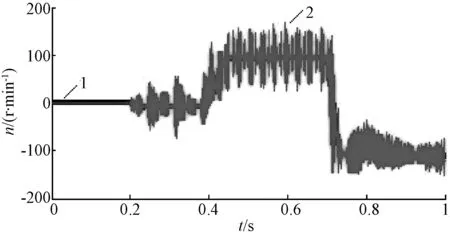
图8 传统模型转速对比图

图中：1为比较平滑曲线表示检测的实际转速；2为波动的曲线表示估计转速。

通过转矩波形和转速对比波形图分析可知：电机在0 s空载启动，0.2 s后突然施加40 N·m的负载转矩，电机转速和估计转速均有轻微变化并且很快恢复，图7在轻微波动后仍趋于零。在0.4 s时，电机转速突然增加，转矩同样突然增加，估计转速立刻响应，跟随实际转速，当转速为100 r/min平稳运行时，转矩变为40 N·m，图7波形轻微波动后趋于零。在0.7 s时，电机反转，此时转矩突然下降，估计转速跟随实际转速伴有轻微波动，当转速为-100 r/min时，转矩恢复40 N·m，图7轻微波动后趋于零。在0.8 s时，转矩增加为60 N·m时，实际转速和估计转速有轻微波动，之后很快恢复跟随，图7轻微波动后趋于零，电机平稳运行。而对应的传统转速估计模型，实际转速和估计转速之差的波形波动比较大，在低速时不能准确的跟随实际转速。在改进型的转速估计波形对比图中，0.2 s、0.8 s时分别突增转矩，转速估计能够在较短时间内恢复跟随，鲁棒性较好；而传统模型的估计波形波动较大，反应时间较长，鲁棒性较差。通过波形对比分析，可以得出改进的电压型转速估计模型相比传统的转速估计模型更能够在低速情况下，估计转速快速响应跟随实际转速，误差在(-1.5～1.5) r/min，精度更高，鲁棒性更好，能够替代速度编码器。

4 结论

提出改进型MRAS转速估计方法，主要针对低速情况下转速估计不准确，采用改进电压型模块，对反电动势的直流和交变产生的误差进行磁链补偿，同时考虑电磁转矩误差，两者并行估计。在低速时能够高精度且稳定的跟随实际转速，并且在突加负载情况下也能快恢复，有更好的鲁棒性。另外，转速估计是在理想状态下运行，转速估计相对准确，在系统实际工作上，转速估计可能会有一定差距，考虑到硬件、环境以及人为因素，需要对Kp、Ki等参数不断调节，选取合适参数以获取最佳转速估计。

[1]洪乃刚.电机运动控制系统[M].北京：机械工业出版社，2015.

[2]王峰，王斌，张杰,等.三电平异步电机的无速度传感器矢量控制系统研究[J].电机与控制应用2011，38(11)：16-19.

[3]王峰，马亮，王斌，等.无速度传感器三电平异步电机矢量控制研究[J].电工电气，2011(11):6-9.

[4]曾树华，李目.基于转子磁链误差的MRAS速度观测器优化设计[J].煤矿机械，2016,37(2):5-7.

[5]蔡文皓，单成龙，范中洋.基于改进定子磁链观测器的MRAS转速估算方法[J].微特电机，2016,44(7):63-71.

[6]周亚丽，李永东，郑泽东.基于MRAS的感应电机无速度传感器矢量控制[J].电气传动，2009,39(4):3-8.

[7]顾华利，张开如，狄东照，等.基于模糊自整定PI永磁同步电机矢量系统的研究[J].电力科学与工程,2016,32(5):14-19.

[8]尹雁,邱阿瑞,王光辉.一种改进的电压型转子磁链估计模型.[J].电气传动，2000,30(6):9-11.

[9]刘和平，王强，余银辉，等.异步电机无速度传感器矢量控制系统研究[J].微电机，2010，43(7)：69-72.

[10]王军，龙驹.异步电机智能控制技术[M].成都：西南交通大学出版社，2014.

[11]梅柏杉，高宁，孟悦然.一种新型的MRAS转速估计法[J].电气传动，2016,46(3):12-14.

[12]姜宏丽，宗伟，刘其辉,等.改进电压模型的异步电机无速度传感器矢量控制[J].电气传动，2015,45(2):8-12.

Improved Speed Estimation Method Based on MRAS

LIU Jian，ZHAO Huadong，WANG Junpeng，WANG Ruoyu，XIN Shuangzhi

(School of Electrical and Automation Engineering，Shandong University of Science and Technology， Qingdao 266590，China)

In view of problem of the relatively big error of the traditional MRAS speed estimation in low speed range and its failure in accurate speed following, a current model is built in this paper which goes through a PI arithmetic compensation voltage model. The voltage type module is improved, and the error produced by the counter electromotive force in dc part is compensated by the field current of rotor flux linkage filtering signal. As for alternating part, the saturated feedback is used for compensation and the observed rotor flux for input. After amplitude limiting, the signal is fed back to compensate the rotor flux to reduce the phase and amplitude distortion. Meanwhile, considering the electromagnetic torque error, these two estimate feedbacks run in parallel. The proposed method is verified by simulation in MATLAB/SIMULINK software, which can effectively reduce the speed estimation error in low speed range and realize speed following accurately, and has better robustness.

MRAS; speed estimation；robustness

10.3969/j.ISSN.1672-0792.2017.05.001

2016-11-21。

TM343

A

1672-0792(2017)05-0001-05