航空火箭弹立靶密集度仿真分析
2017-06-23黄若超高宏超何庆华
黄若超,高宏超,毛 瑞,何庆华
(中国兵器工业第203研究所,西安 710065)
航空火箭弹立靶密集度仿真分析
黄若超,高宏超,毛 瑞,何庆华
(中国兵器工业第203研究所,西安 710065)
炮口速度及转速对航空火箭弹的立靶密集度有非常重要的影响。为了提高航空火箭弹的立靶密集度,文中以常规火箭弹的散布理论和外弹道理论为基础,对各随机因素进行分析,建立符合其特征的数学模型,运用蒙特卡洛法进行数学仿真,研究不同炮口速度与转速对航空火箭弹立靶密集度的影响,结果表明提高炮口速度有利于提高立靶密集度,而炮口转速则需要控制在合适范围内,此结果对今后工程运用提供了理论参考。
炮口速度;炮口转速;立靶密集度;蒙特卡洛法
0 引言
航空火箭弹是武装直升机配备的主要武器之一,因威力大、射程远、战斗部多样化、成本低廉,广泛的用于攻击地面上的各类目标。但是航空火箭弹的落点散布大,密集度低,影响了其作战效能。
文中对弹道偏差作了全面分析,建立了弹体气动模型、发动机模型、阵风模型和大气模型等,为了体现实际弹体的差异带来的弹道偏差,建立了偏差的随机项扰动模型[1],结合航空火箭弹结构参数与气动计算结果,利用C++语言编程求解运动方程,运用积分、插值、散布统计、分布拟合检验等方法对偏差扰动过程进行了弹道仿真模拟。根据蒙特卡洛仿真与飞行试验结果,分析了炮口速度和炮口转速对航空火箭弹立靶密集度的影响。
1 立靶密集度简介
文中提到的立靶密集度是描述航空火箭弹散布的常用指标,是指在立靶密集度试验中,随机弹着点相对火箭弹平均弹着点的偏离度[2],也称为圆概率误差,用E表示,其数值越小表示立靶密集度越好。
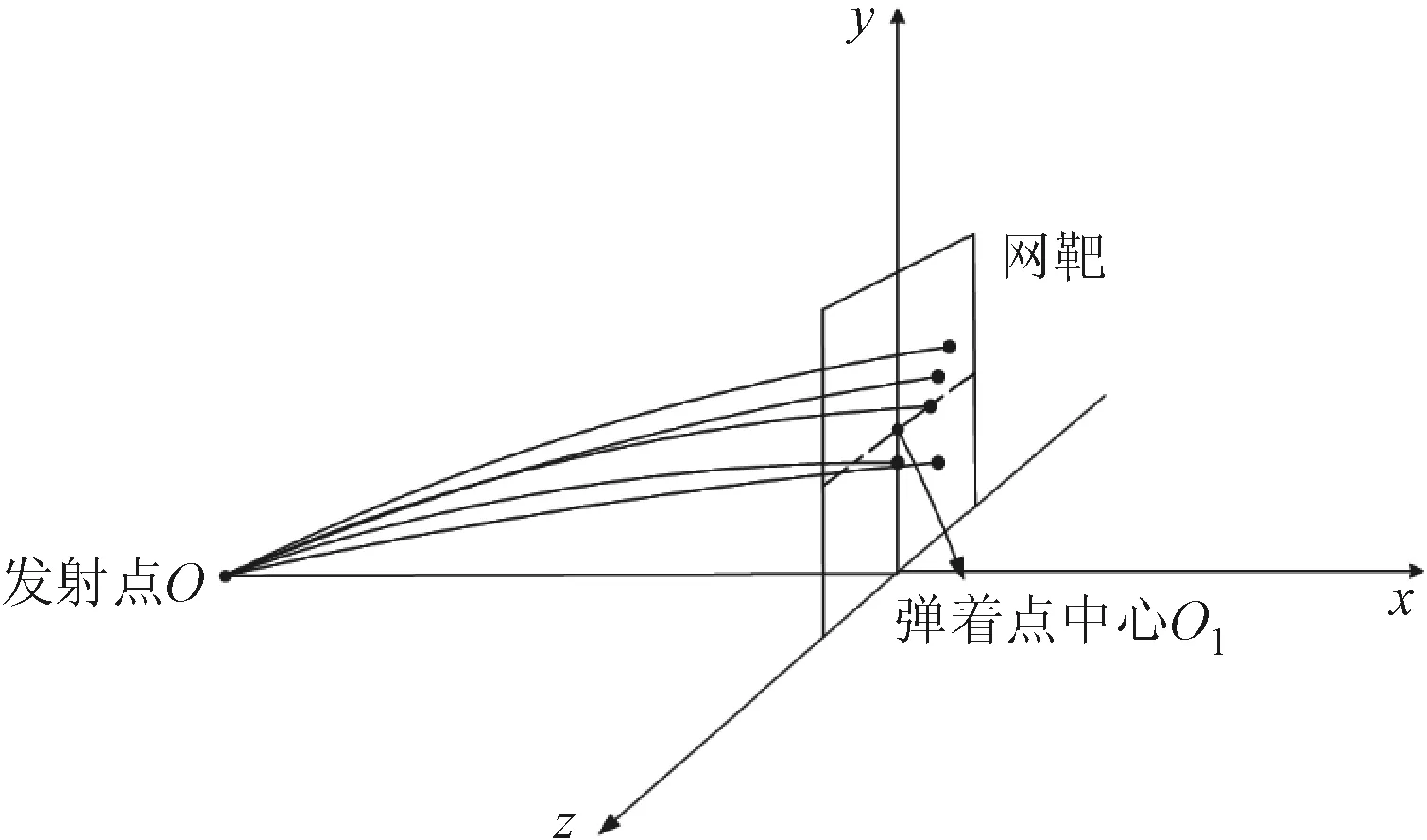
图1 立靶密集度试验示意图
立靶密集度与高度散布标准差Sy和横向散布标准差Sz密切相关[3]:
E=0.674 5×
2 仿真与结果分析
仿真试验基于以下假设:
1)立靶处散布仅与上文提到的随机项扰动有关,且其扰动规律不因炮口速度及转速的改变而改变;
2)各项扰动模型参数根据试验数据建模仿真拟合得到。
2.1 偏差项扰动模型
利用蒙特卡洛法仿真时,随机误差主要考虑推力偏心角、偏心距,结构参数差异,温度气象差异,以及发射时俯仰、偏航的初始扰动跳动量差异。主要扰动模型建立如下[4]:
1)俯仰、偏航初始扰动[5]
俯仰、偏航的初始扰动均服从正态分布,其标准差根据某型航空火箭弹飞行试验多发弹落点,经数学仿真拟合确定,并且其标准差不因炮口速度改变而变化。
2)随机阵风扰动
随机阵风风速矢量W可表示为常值风速Wc和随机风速ΔW的矢量和:
W=Wc+ΔW
其中ΔW是沿时间和空间随机变化的。随机风速ΔW的标准差为σΔW:
σΔW=
模型中随机阵风的大小服从正态分布,标准差按照上式随机生成,随机阵风的方向为水平方向服从均匀分布(不考虑垂直风Wy)。
3)推力偏心角、偏心距扰动
推力偏心距d服从于正态分布,其分布特征用标准差σd表示。
初始偏心角δ是在[0,2π]内服从均匀分布的随机变量。
4)静不平衡扰动
质心偏离几何轴线的线偏差h0服从正态分布,分布特性σh大小由某航空火箭弹弹体参数确定。
质心偏离方位是服从[0,2π]区间的均匀分布的随机变量。
5)动不平衡扰动
惯性中心主轴在纵向对称面的投影与弹体纵轴的夹角λ和惯性中心主轴与弹体纵向对称平面之间的夹角μ服从正态分布,其标准差分别为σλ和σμ。
6)气动偏差扰动[6]
阻力偏差是服从正态分布的随机变量,其分布特性用标准差σX表示。
2.2 偏差项分析与仿真
建立火箭弹弹道偏差复数模型[7],对方程进行简化求解,分别得出各项扰动所引起的弹道偏差复式方程,从而进一步分析影响原因:
航空火箭弹的初始角速度是初始扰动引起散布的主要原因,且当S≪1(S为陀螺稳定因子)时,偏角引起的扰动基本等同非旋转弹情况,因此初始扰动引起的偏角复式方程为:
横风引起的偏角复式方程为:
推力偏心距引起的偏角复式方程为:
动不平衡引起的偏角复式方程为:
气动偏心引起的偏角复式方程为:
建立偏差项仿真模型[8],图2是航空火箭弹在不同炮口速度下的攻角值,可以看出随着炮口速度的增加,航空火箭弹攻角值减小,即炮口速度大的航空火箭弹稳定性更好。
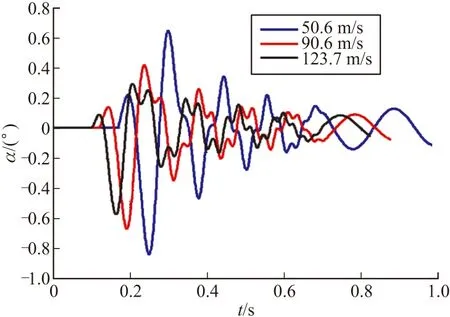
图2 不同炮口速度下攻角值
通过图3可以看出炮口转速较小时,推力偏心矩周期长,引起的角偏差大,散布就大,当增加炮口转速到一定值时,推力偏心矩周期趋于相同,引起的角偏差也就趋于相同,从而当炮口转速增大到一定值时,立靶密集度几乎不再变化。
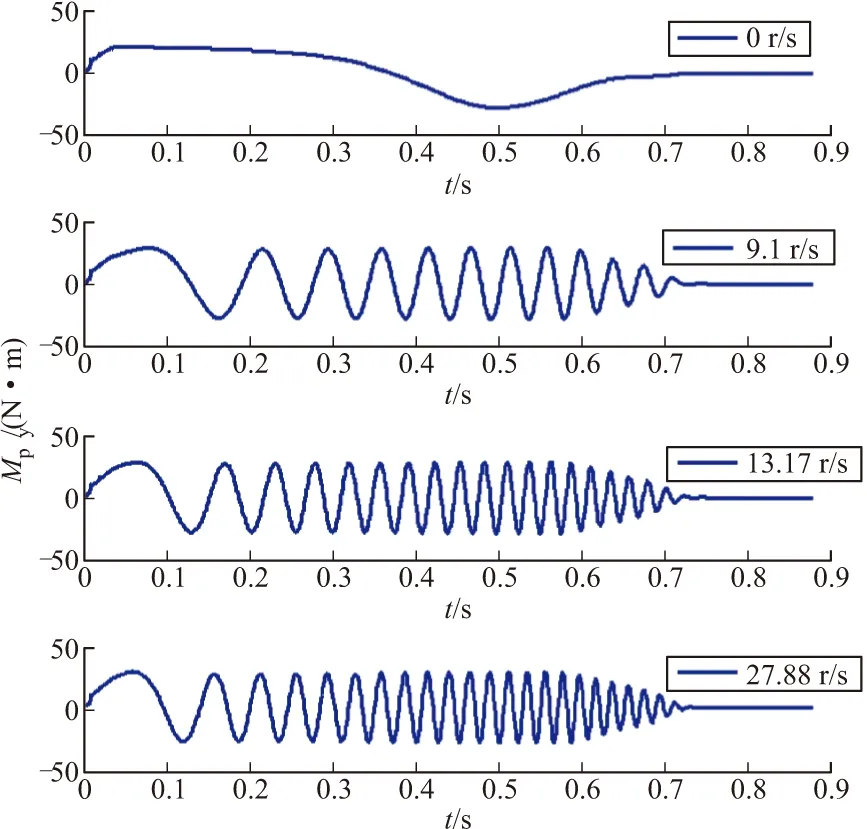
图3 不同炮口转速下y轴方向推力偏心力矩
根据图4可看出,随着炮口转速的增大,动不平衡扰动力矩增大,即动不平衡引起的角偏差增大,散布变大。因此当转速增加到一定值时,立靶密集度反而随着转速的增加而变差。
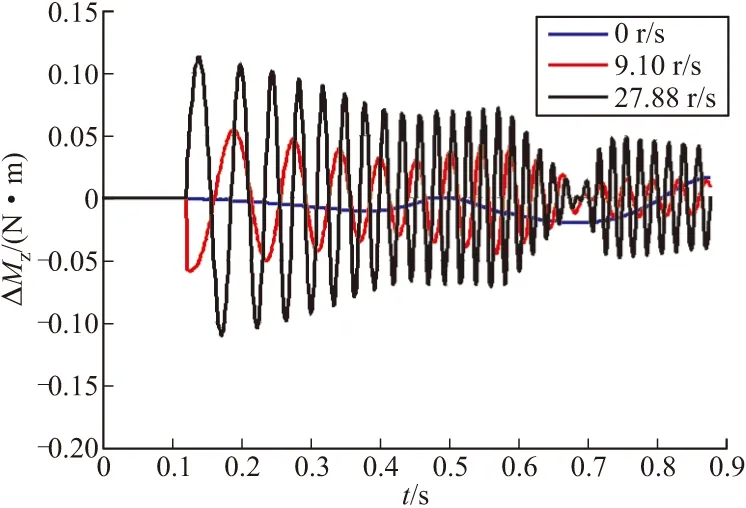
图4 不同炮口转速下动不平衡扰动力矩
2.3 立靶密集度仿真
首先验证炮口速度对立靶密集度的影响。在总冲不变的基础上,建立5组推力模型,获取不同炮口速度,利用蒙特卡洛打靶法,针对不同初速分别设置200条弹道仿真,仿真结果如表1所示。
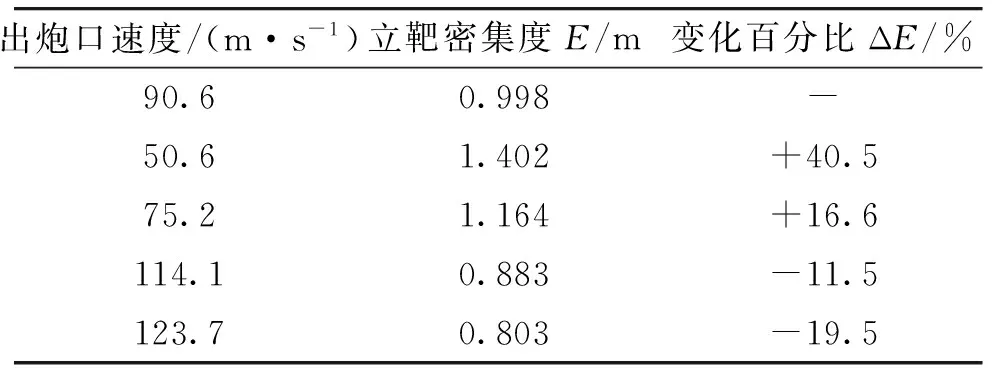
表1 炮口速度变化对立靶密集度的影响
其次验证不同炮口转速对立靶密集度的影响。建立赋旋角影响炮口转速数学模型。通过调整赋旋角角度来控制出炮口转速,初始条件不变,利用蒙特卡洛打靶法,针对不同炮口转速分别设置200条弹道仿真,仿真结果如表2所示。
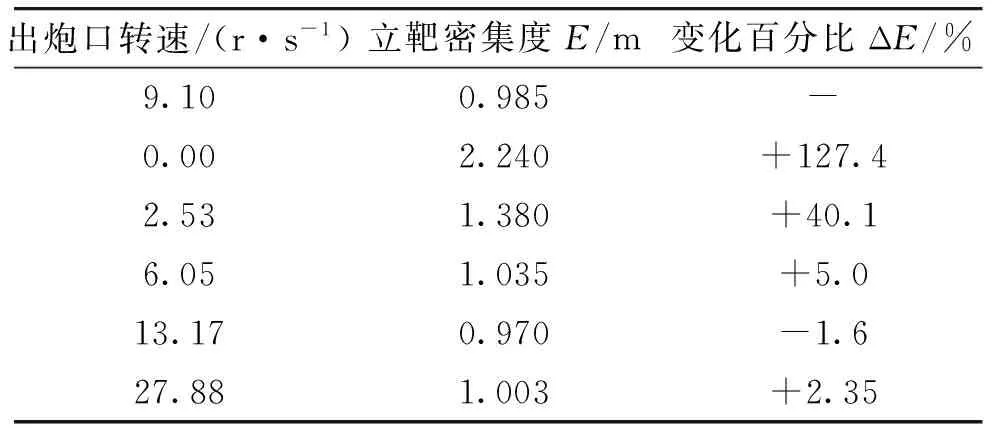
表2 炮口转速变化对立靶密集度的影响
根据表1、图5,可看出立靶密集度随着炮口速度的增加而提高。
根据表2、图6可看出,在较低的转速范围内,立靶密集度随着炮口转速的提高而提高,当炮口转速继续增加时,对立靶密集度影响几乎可以忽略。文中建立的航空火箭弹模型静稳定度很大,动不平衡引起的密集度变化几乎不能体现。
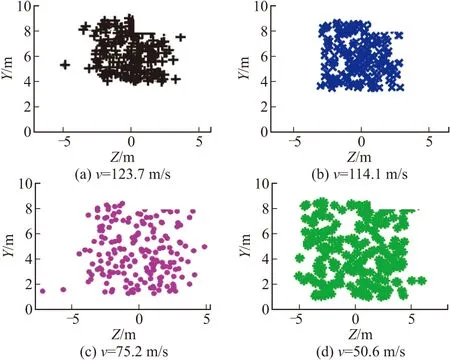
图5 不同炮口速度靶面弹着点坐标
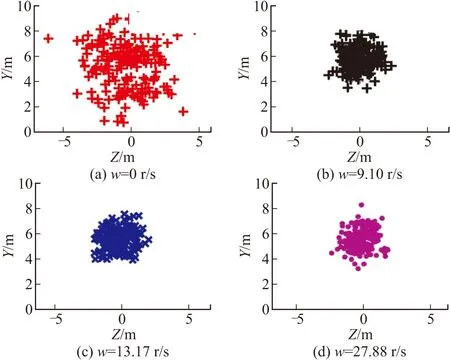
图6 不同炮口转速靶面弹着点坐标
3 立靶密集度试验与分析
为了验证偏差项仿真与蒙特卡洛仿真结果的正确性,以某型航空火箭弹为分析对象,进行飞行试验验证。
设计不同推力方案,通过立靶密集度试验,验证出炮口速度对密集度的影响,结果如表3所示。
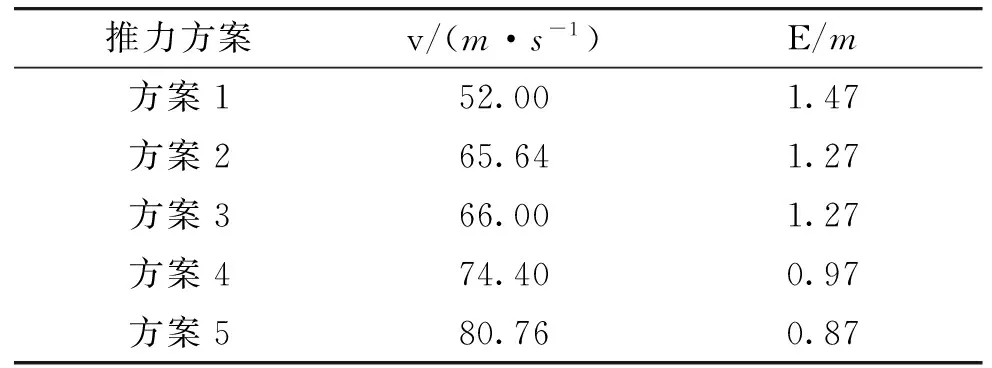
表3 不同出炮口速度立靶测试结果
设计不同赋旋角方案,通过立靶密集度试验,验证了出炮口转速对密集度的影响,测试结果如表4所示。

表4 不同出炮口转速下立靶测试结果
根据仿真与试验结果可知,立靶密集度随炮口速度的增加而提高。炮口转速需控制在合适范围内,因为随着转速的增大立靶密集度变化不大,反而牺牲射程。航空火箭弹静稳定度较高,所以转速变化带来的动不稳定影响不明显。理论分析与试验结果一致。
4 结论
文中分析了炮口速度与炮口转速对航空火箭弹立靶密集度的影响。结果表明,提高炮口速度可以有效提高立靶密集度,而炮口转速则需要合理设计,尤其对于静稳定度不高的航空火箭弹,能使其同时兼顾立靶密集度与动不平衡扰动带来的动不稳定影响。
[1] 高帅. 远程火箭弹的散布研究 [D]. 南京: 南京理工大学, 2004.
[2] 郑永杰. 减小航空火箭弹散布方法的研究及其优化 [D]. 南京: 南京理工大学, 2003.
[3] 王宝元, 衡刚, 周发明, 等. 基于坐标极差估算高炮立靶密集度的方法 [J]. 测试技术学报, 2014, 28(4): 356-357.
[4] 钱杏芳. 导弹飞行力学 [M]. 北京: 北京理工大学出版社, 2008: 137-148.
[5] 王志军, 赵文宣. 火箭弹起始扰动数值仿真研究 [J]. 弹道学报, 1996, 8(3): 70-73.
[6] 汤江河. 影响直升机载航空火箭射击精度的因素分析 [D]. 南京: 南京理工大学, 2007.
[7] 杨绍卿. 火箭外弹道偏差与修正理论 [M]. 北京: 国防工业出版社, 2011: 98-144.
[8] 毛保全, 邓威, 冯帅, 等. 远基于多学科协同仿真的立靶密集度计算方法 [J]. 计算机仿真, 2016, 33(1): 20-22.
Simulation and Analysis of Vertical Target Dispersion of Airborne Rocket
HUANG Ruochao,GAO Hongchao,MAO Rui,HE Qinghua
(No.203 Research Institute of China Ordnance Industries, Xi’an 710065, China)
The muzzle velocity and the muzzle rotating speed had very important influence on the vertica target dispersion of airborne rocket. In order to improve the vertical target dispersion of airborne rocket, base on the dispersion theory and exterior ballistic theory of conventional rocket, the random factors were analyzed to establish the mathematical model in line with its characteristics. By using the Monte Carlo method for mathematical simulation, the influence of different muzzle velocity and muzzle rotating speed on the vertica target dispersion of airborne rocket was studied. The results showed that increasing muzzle velocity was helpful to improve the vertical target density, while muzzle speed needed to be controlled within the appropriate range. This conclusion provided theoretical references for future engineering applications.
muzzle velocity;muzzle rotating speed;vertical target dispersion;Monte Carlo method
2016-11-03
黄若超(1991-),女,陕西蓝田人,助理工程师,硕士研究生,研究方向:航空火箭弹总体技术。
V435;V211.48
A
