制导刚度受限时不同结构驾驶仪对制导精度的影响分析

栗金平,黎海青,张晓峰,张正同

(中国兵器工业第203研究所,西安 710065)

制导刚度受限时不同结构驾驶仪对制导精度的影响分析

栗金平,黎海青,张晓峰,张正同

(中国兵器工业第203研究所,西安 710065)

为有效提高比例导引制导反坦克导弹近射程作战能力,需研究制导刚度受限时,不同结构自动驾驶仪对制导精度的影响。首先对反坦克导弹比例导引制导系统形式进行了阐述;然后给出常用的自动驾驶仪,并对不同自动驾驶仪的动态性能进行对比分析;最后分析对应的线性比例导引制导系统模型,得出在制导刚度受限条件下,阻尼回路自动驾驶仪对应制导系统制导精度最高。

比例导引;自动驾驶仪;频域分析;时域分析

0 引言

为有效提高采用比例导引制导反坦克导弹近射程作战能力,需要研究影响导弹近射程制导精度的因素。自动驾驶仪作为制导系统的内回路,核心任务是保证导弹精确、鲁棒的跟踪制导系统生成的输入指令,使导弹根据控制指令产生控制力矩和控制力来改变导弹的攻角,进而改变速度矢量方向,使导弹稳定飞行直至命中目标[1]。自动驾驶仪不同,其动态性能必然不同,对制导系统的影响也不尽相同。

目前,根据自动驾驶仪的结构种类,比例导引制导反坦克导弹制导系统形式主要有3种:一是比例导引回路+开环自动驾驶仪;二是比例导引回路+阻尼回路驾驶仪;三是比例导引回路+经典三回路过载驾驶仪。文中主要分析反坦克导弹制导刚度受限时,即攻击近射程目标,比例导引段时间不能充分满足弹道收敛要求时,不同驾驶仪对反坦克导弹近射程制导系统性能的影响。

1 反坦克导弹常用自动驾驶仪

反坦克导弹自动驾驶仪,主要是指导弹的执行机构、弹体及相应的控制器等构成的闭环系统。

1.1 开环自动驾驶仪

开环自动驾驶仪由过载指令控制增益、舵机和弹体组成,结构形式如图1所示。

图1 开环自动驾驶仪结构框图

图1中:nyc为法向过载指令;ny为法向过载响应;ωz为俯仰角速度;Kn1为过载指令控制增益。

开环自动驾驶仪接收制导系统生成的比例导引过载指令,通过过载指令控制增益进行放大,得到舵机指令,舵机根据指令产生控制力矩,操纵导弹姿态旋转,实现需用过载。但是该控制系统传递函数是弹体传递函数,为了获得适当的末制导系统特性,弹体必需稳定。另外,为获得适当的有效导航比,要求精确确定导弹的气动特性[2]。

1.2 阻尼回路自动驾驶仪

为了使自动驾驶仪具有良好的阻尼特性,在开环自动驾驶仪的基础上增加阻尼回路,即构成了阻尼回路自动驾驶仪,结构形式如图2所示。

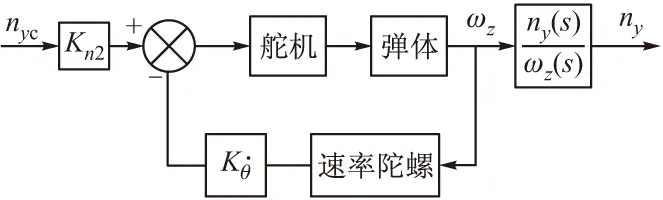
图2 阻尼回路自动驾驶仪结构框图

阻尼回路自动驾驶仪工作原理与开环近似,形成过载控制指令后,与阻尼回路控制指令综合后形成舵机指令,操纵导弹姿态旋转,实现需用过载。该控制系统的动态响应基本上是具有理想阻尼和有比弹体自然频率稍高的二阶传递函数的响应[2]。但是该控制系统能够适应弹体的静不稳定范围是有限的[1]。

1.3 经典三回路过载驾驶仪

经典三回路过载驾驶仪相对阻尼回路自动驾驶仪,增加了角速度积分增稳回路和过载反馈回路,结构形式如图3所示。

经典三回路过载驾驶仪使用比例导引过载指令和实际过载反馈之间的误差形成过载控制指令,综合角速度积分增稳回路指令和阻尼回路指令形成舵机控制指令。优点是既可以保证导弹飞行范围内的有效导航比,又能适应静不稳定弹体的控制;缺点是需要的测量信息较多,实现时相对复杂。

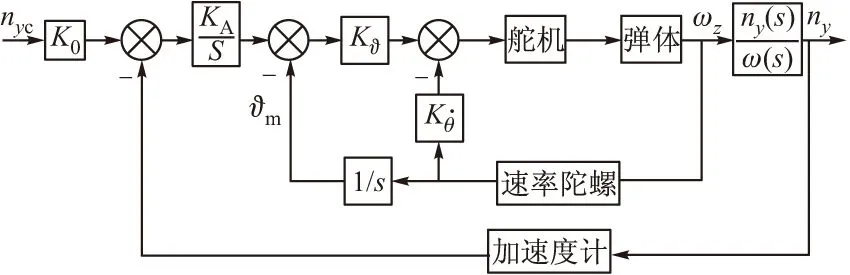
图3 经典三回路过载驾驶仪结构框图

1.4 自动驾驶仪性能对比

以某型反坦克导弹气动外形为参考,选取飞行海拔高度为1 400 m、飞行速度为0.3Ma作为设计特征点,对3种自动驾驶仪线性模型进行对比分析。经计算,特征点对应的动力学系数a1=0.63,a2=98.73,a3=170.86,a4=1.03,a5=0.33,因此对应的弹体传递函数为:

弹体阻尼系数为0.083。舵机带宽为20 Hz,以理想二阶环节描述其特性,对应的传递函数为:

对设计的3种驾驶仪线性模型进行时域分析,阶跃响应曲线如图4所示。根据结果可知,阶跃响应上升时间最短的为开环自动驾驶仪,最长的为经典三回路过载驾驶仪,但是由于开环自动驾驶仪除了过载指令控制增益外,传递函数为纯弹体传递函数,而弹体阻尼系数仅为0.076,所以其阶跃响应超调大,调节时间长,动态性能差。阻尼回路自动驾驶仪与经典三回路过载驾驶仪相比,阻尼回路控制增益相同,但是前者对应的时间常数短,响应快,对气动参数、速度和高度的准确性要求更高。

图4 3种自动驾驶仪阶跃响应曲线图

2 驾驶仪对制导精度的影响分析

反坦克导弹比例导引制导系统包括平台式导引头、低通滤波器、比例导引律、自动驾驶仪、导弹运动学和弹目相对运动学。文中分别通过频域和时域分析不同结构驾驶仪对制导精度的影响。

2.1 制导系统模型

开环自动驾驶仪、阻尼回路自动驾驶仪和经典三回路过载驾驶仪对应的线性制导系统模型分别为图5～图7所示。

图5 开环自动驾驶仪对应制导系统模型

图6 阻尼回路自动驾驶仪对应制导系统模型

图7 经典三回路过载驾驶仪对应制导系统模型

2.2 制导系统频域分析

图8 开环自动驾驶仪对应制导系统bode图

制导系统开环bode图表征此飞行状态下,比例导引制导系统的稳定性。由bode图可看出,开环自动驾驶仪和经典三回路过载驾驶仪对应的制导系统已经不稳定,即在选取的飞行特征点下,开环自动驾驶仪和经典三回路过载驾驶仪对应比例导引制导系统的末端发散距离大于50 m。由于阻尼回路自动驾驶仪对应比例导引制导系统弹道末端发散最晚,因此3种制导系统在相同导航比条件下,阻尼回路驾驶仪对应比例导引制导系统的制导精度最高。

图9 阻尼回路自动驾驶仪对应制导系统bode图

2.3 制导系统时域分析

导弹攻击近射程目标时,飞行时间短,对弹道的快速收敛有极高的要求,自动驾驶仪结构不同,制导系统的收敛速度也不相同,导致制导精度也不相同。下面把弹目距离RTM看作变量,分析不同结构自动驾驶仪对比例导引制导系统收敛速度的影响。

图10 经典三回路过载驾驶仪对应制导系统bode图

图11 RTM0=200 m时不同制导系统时域响应

通过对3种制导系统进行频域和时域分析得出,相同条件下,阻尼回路自动驾驶仪对应比例导引制导系统弹道末端发散最晚,弹道收敛速度最快,因而在制导刚度受限时,其制导精度最高。

3 结论

文中首先阐述了反坦克导弹比例导引制导系统的实现形式;然后对常用自动驾驶仪的动态性能进行对比分析;最后对不同驾驶仪对应的比例导引制导系统模型进行频域和时域分析,得出末制导时间受限时,阻尼回路自动驾驶仪对应的比例导引制导系统弹道末端发散最晚,收敛速度最快,因而最适用于攻击近射程目标。

[1] 林德福, 王辉, 王江, 等. 战术导弹自动驾驶仪设计与制导律分析 [M]. 北京: 北京理工大学出版社, 2012: 4.

[2] 杨军, 杨晨, 段朝阳, 等. 现代导弹制导控制系统设计 [M]. 北京: 航空工业出版社, 2005: 49.

[3] 刘晓侠, 杨凯, 严宪军, 等. 反坦克导弹导引回路设计与仿真 [J]. 弹箭与制导学报, 2009, 29(6): 38-40.

[4] 夏群力, 郭涛, 祁载康, 等. 空地导弹对应不同驾驶仪下的中制导高度控制回路设计 [J]. 系统仿真学报, 2008, 20(24): 6763-6766.

[5] 杨广慧, 孙友, 巩庆海, 等. 某类比例导引飞行器的制导回路稳定性分析方法 [J]. 航天控制, 2013, 31(1): 11-14.

The Impact Analysis of Autopilots with Different Structures on Guidance Accuracy when the Guidance Stiffness was Constrained

LI Jinping,LI Haiqing,ZHANG Xiaofeng,ZHANG Zhengtong

(No.203 Research Institute of China Ordnance Industries, Xi’an 710065, China)

In order to improve the combat capability of the anti tank missile using the proportional navigation in the near range, the influence of the autopilots with different structures on the guidance accuracy was studied. First, the form of the anti tank missile’s guidance system using the proportional navigation was described. Then, the common autopilot was given, and the dynamic performance of different autopilots was compared and analyzed. At last, the corresponding linear proportional navigation guidance system model was analyzed. It was concluded that the guidance precision of corresponding guidance system of damping loop autopilot was the highest under the condition of limited guidance stiffness.

proportional navigation; autopilot; frequency domain analysis; time domain analysis

2016-03-08

栗金平(1984-),男,河南商丘人,工程师,硕士,研究方向:导弹精确制导与控制。

TJ765

A